含高比例分布式光伏的配電網多目標概率規劃方法

惠慧,李蕊,朱逸鏑,張育煒,李天翔,陸文標,肖遷

(1.中國電力科學研究院有限公司,北京 100192; 2.天津大學 未來技術學院,天津 300072;3.天津大學 電氣自動化與信息工程學院,天津 300072)

0 引 言

在全球氣候變化和環境污染問題加劇的背景下,推動可再生能源的發展已變得至關重要[1]。分布式光伏具有配置靈活、用地面積小等優點,且鄰近負荷中心利于消納[2],近年來,其在新型配電網中的接入比例迅速增長[3]。然而,分布式光伏出力受天氣、季節等因素影響,具有不確定性,使配電網的規劃運行面臨嚴峻挑戰。傳統配電網規劃(如多場景規劃等)通常將不確定性規劃模型轉化為等價的確定性規劃模型[4],模型的精度難以保證,且對于不確定性因素的考慮不夠全面。因此,亟需開展考慮分布式光伏不確定性的配電網概率規劃研究。現有配電網分布式光伏規劃方面研究主要體現在兩個方面:一為考慮配電網運營投資成本的經濟性規劃[5],二為考慮高比例分布式光伏接入造成運行指標劣化的可靠性規劃[6]。

在經濟性規劃方面[7-11],分布式光伏的大規模接入使得配電網的規劃成本大幅上升,為提升配電網規劃運行經濟效益,有諸多研究提出規劃成本優化方法。文獻[7]從不同主體的利益角度出發,針對配電網擴展規劃問題,建立基于主從博弈的雙層優化模型。文獻[8]通過主成分-高斯混合聚類算法對數據進行場景降維,以總成本最小為目標構建規劃模型,為配電網規劃提供典型場景生成方法。文獻[9]提出一種考慮綜合能源系統設備和配電網變電站容量協同規劃的多場景規劃方法,實現了投資成本與運行成本的協同優化。文獻[10]基于全壽命周期成本管理對配電網發展規劃方案進行優化。文獻[11]提出一種考慮源網荷協同的配電網分布式光伏儲能多目標優化配置方法,提高了優化配置方案的經濟性,實現了源網荷協同規劃。然而,上述文獻大多并未考慮光伏滲透率的提升和運行指標的優化。

在可靠性規劃方面,隨著分布式光伏接入比例的提升,其無序接入造成了配電網電壓的劇烈波動與網損的急劇攀升,為使高比例分布式光伏接入后的配電網能夠安全穩定運行,需對分布式光伏進行合理配置[12-17]。文獻[12]提出一種風-光-儲兩階段規劃配置方法,考慮有功網損靈敏度和系統電壓穩定指標最大等建立多目標規劃模型,實現了配電網運行情況的改善。文獻[13]引入遺傳算法對PSO算法進行改進,兼顧電壓越限風險的降低與光伏滲透率的提升。文獻[14]考慮經濟性、環保性、安全性等指標,對分布式能源進行優化配置,為多指標評價的配電網規劃奠定基礎。文獻[15]基于信息熵的場景提取方法,建立多場景光伏及儲能選址定容規劃模型,實現配電網運行的經濟性與可靠性提升。文獻[16]利用聚類分析確定規劃場景,基于多種群牽引差分進化算法,實現全年網損與電壓偏差最小的優化規劃。文獻[17]基于節點脆弱性評估對配電網分布式光伏進行優化配置,改善了配電網的節點電壓與網損情況。上述文獻考慮了高比例分布式光伏接入后造成的可靠性問題,但仍基于確定性出力場景進行規劃,對分布式光伏不確定性的考慮不夠全面,所得結果與實際運行情況不匹配。

為提升分布式光伏不確定性場景下的配電網運行穩定性,降低配電網經濟成本,文章提出一種含高比例分布式光伏的配電網多目標概率規劃方法。首先,基于光伏出力數據,采用K-means聚類與概率潮流生成光伏不確定性場景,模擬分布式光伏實際運行情況;在此基礎上,計及建設成本、光伏滲透率、概率潮流下的電壓偏差指數等指標建立雙層概率規劃模型,引入概率潮流表征光伏出力對系統的影響,從而提升配電網對不確定性光伏出力的適應能力;最后,采用安徽某地光伏出力作為典型數據,以IEEE 33節點系統為算例開展了多場景算例分析。

1 含高比例分布式光伏的配電網不確定性場景構建

為實現考慮光伏不確定性的配電網概率規劃,需對分布式光伏實際運行情況進行模擬,文章基于K-means聚類、概率潮流等方法,提出含高比例分布式光伏的配電網不確定性場景構建方法。

1.1 光伏出力概率模型

光伏發電系統輸出功率受到天氣、季節等因素的影響,具有不確定性。研究表明,Beta分布對光照強度的擬合效果較好[18],其概率密度函數的表達式可以通過光照強度的平均值和標準差近似計算得到,表達式如下:

(1)

(2)

式中r和rmax分別為實際光照強度和最大光照強度;α和β為形狀參數;μr和σr分別為光照強度的平均值和標準差。

光伏出力與光照強度之間滿足線性關系,因此光伏出力同樣服從Beta分布,其概率密度函數為[19]:

(3)

式中PPVG為分布式光伏機組的輸出功率,PPVG=rAη,其中r為光照強度,A為電池等效面積,η為光電轉換效率;PPVG,max為分布式光伏機組的最大輸出功率。

1.2 不確定性光伏出力場景生成

1.2.1 數據預處理

由于實際的光伏數據中存在超出正常日照時間范圍、量級有明顯差異等不符合實際的錯誤數據,因此有必要對光伏數據進行預處理,以提高數據的可用性和準確性。

文章數據預處理包括異常值處理和數據轉換兩個步驟。具體如下:

1)異常值處理:首先通過經驗判斷結合統計方法辨識數據中的異常值,對不同季節日出、日落時段前后的數據進行辨識;其次,通過數據對比篩選出數據庫中不符合實際的數據;最后,采用刪除異常值方法移除數據集中的異常值,并對缺失的數據根據辨識結果采取插值處理,將日落時間段缺失數據置零,日出時間段缺失數據替換為鄰近值;

2)數據轉換:首先,將采集數據輸入數據庫并統一數值格式;其次,將不同時間尺度的連續出力數據轉換為1 h時間尺度的出力數據集;最后,判斷數據集規模并轉換為相應的日出力數據集。

1.2.2K-means聚類方法

由于實際的光伏出力場景數據量較為龐大,基于全部場景數據進行概率模型建模計算效率較低,需要對其進行場景削減。文章采用K-means聚類方法進行場景削減,該算法基于相似性原則,旨在確保同一類的光伏出力數據點高度相似,而與其他類的光伏出力數據點有明顯差異[20]。具體步驟如下:

1)隨機選取樣本中的k個點作為質心;

2)分別計算其他樣本到初始質心的距離,將樣本分類到與之距離最近的質心類別,樣本距離表達式為:

(4)

式中xi和yi分別為每個樣本在空間中的坐標;

3)對每個類別求平均值,求解出新的聚類質心;

4)與前一次計算得到的k個聚類質心比較,若聚類質心發生變化,轉步驟2),否則轉步驟5);

5)當質心不再變化時,停止并輸出聚類結果。

1.2.3 最佳聚類數目確定

在K-means算法中,簇的個數(即聚類數目)k是影響聚類結果的重要因素,需要人為輸入進行確定。若k的取值過大則聚類失去意義,若取值過小則聚類特征不夠顯著。肘部法是確定k值的一種常見方法[20],具有直觀、高效的特點,同時無需復雜的數學計算或算法,所需計算資源少,適合處理光伏出力數據等大規模數值型數據,故文章采用此方法確定最佳聚類數目。

肘部法利用不同k值及其對應的誤差平方和(sum square error,SSE)評價聚類效果。SSE值越小表示每一類數據相似程度越高,聚類效果越好,計算公式為:

(5)

式中Ci代表第i個簇;p為簇Ci里的樣本點;mi為簇的質心。

通常SSE值隨著k值增大而減小,其對應圖像存在下降拐點,在拐點處增加k值所帶來的聚類效果提升相對較小。由于k值不宜過大,所以SSE下降拐點對應的k值為最佳聚類數[20]。

1.3 概率潮流計算

概率潮流計算是一種計及光伏出力等不確定性因素,并表征其對系統影響的潮流計算方法[21]。相比傳統的潮流計算方法,概率潮流計算考慮到光伏出力的概率特性,所得結果更符合含分布式光伏配電網實際運行情況[22],為所提概率規劃模型提供了數據基礎。

概率潮流算法包含模擬法、近似法和解析法,其中,蒙特卡洛模擬法因具有高計算精度的優勢[22],文章采用蒙特卡洛模擬法求解概率潮流問題。

蒙特卡洛模擬法是一種基于隨機抽樣的數值計算方法[23],通過在隨機變量的可能分布中進行隨機抽樣,模擬出大量可能的系統運行狀態,其步驟如下:

在包含m個單元的系統中,Xi=(X1,X2,…Xm)代表每個子單元的狀態變量向量,xi=(x1,x2,…xm)為該向量的數學表達式。當這些單元相互獨立時,其聯合概率分布P(X)為:

(6)

理論上,對所有樣本抽樣后可以根據其聯合概率分布計算期望值和方差,然而,由于實際采集樣本數量的限制,期望值和方差通常為估計值:

(7)

(8)

式中E(F)為實驗函數的期望;V(F)為實驗函數的方差;Ns為樣本數量;Fi(X)為第i次采樣中獲得的實驗函數。

蒙特卡洛概率潮流計算包括確定計算參數、進行蒙特卡洛模擬、進行潮流計算和統計概率分布等步驟,具體如下:

1)確定計算參數。包括發電機出力上下限、節點負荷、分布式光伏概率分布等參數;

2)進行蒙特卡洛模擬,生成概率樣本。通過隨機抽取分布式光伏出力的概率樣本,得到不同概率場景;

3)對于每個概率樣本,進行潮流計算。根據樣本中的負荷消耗和分布式光伏出力,計算電力系統中各節點的電壓和功率;

4)統計各節點的電壓和功率的概率分布。根據蒙特卡洛模擬的結果,得到配電網中各節點電壓和網損的概率密度函數(probability density function,PDF)及累積分布函數(cumulative distribution function,CDF)。PDF與CDF將滿足以下關系:

(9)

式中X為狀態變量,文章中指節點電壓及網損;FX(x)為狀態變量X的CDF;fX(x)為狀態變量X的PDF。

2 含高比例分布式光伏配電網雙層概率規劃模型

在分布式光伏的出力波動影響下,配電網的規劃成本攀升,運行穩定性降低。為實現含高比例分布式光伏配電網的經濟可靠規劃,文章基于前述不確定性場景,建立含高比例分布式光伏配電網雙層概率規劃模型。

含高比例分布式光伏配電網雙層概率規劃關系如圖1所示。

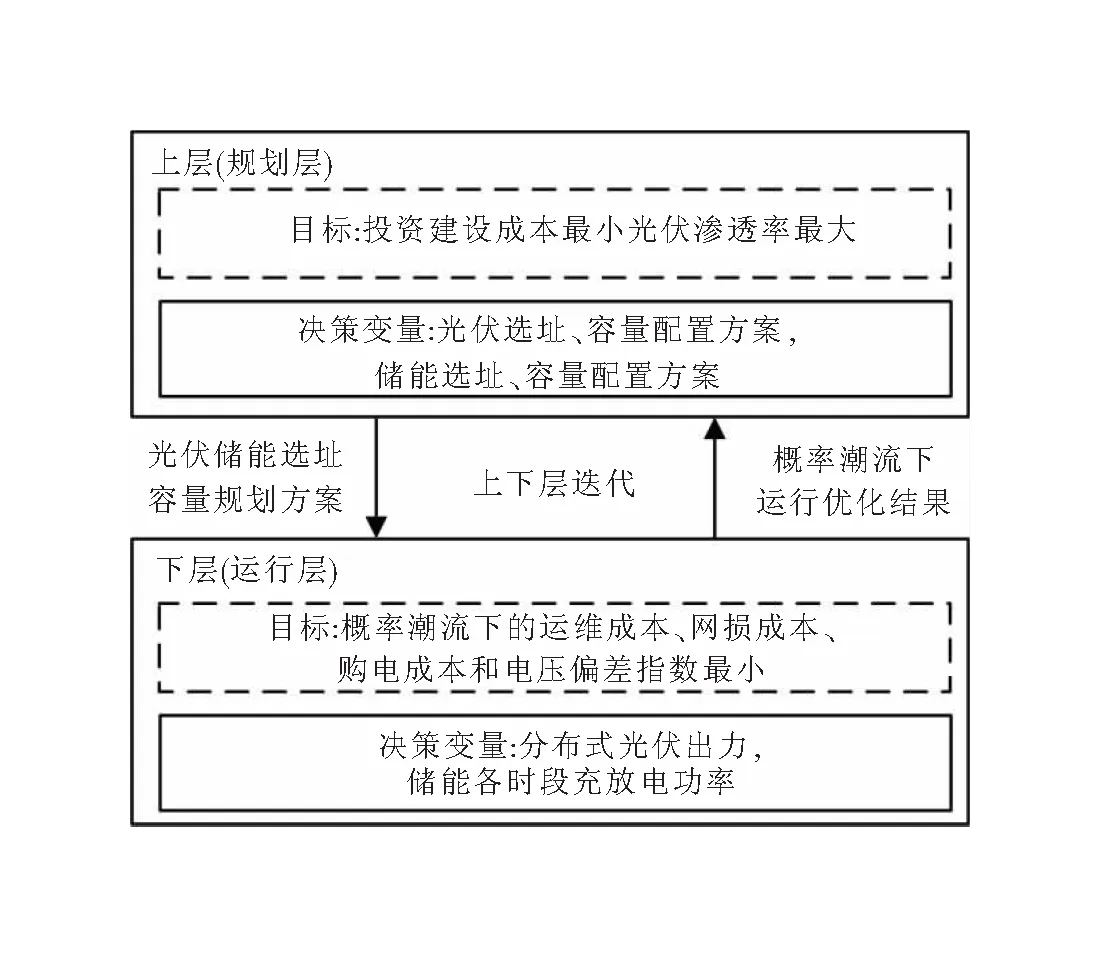
圖1 雙層概率規劃關系圖

其中,模型上層為規劃層,以投資建設成本最小和光伏滲透率最大為目標,確定光伏、儲能的選址與容量配置方案;下層為運行層,考慮分布式光伏出力的不確定性,量化光伏出力、系統網損和電壓產生的隨機波動,以概率潮流下的運維成本、網損成本、購電成本和電壓偏差指數最小為目標,優化分布式光伏出力以及儲能各時段充放電功率。運行過程中,上層將分布式光伏與儲能配置方案傳遞給下層,作為下層的初始條件,下層基于上層的結果對分布式光伏與儲能進行運行優化,并將運行優化結果傳遞給上層。

2.1 規劃層模型

2.1.1 目標函數

由于投資成本和光伏滲透率量綱不同,需要進行歸一化后建立目標函數。

y=(x-xmin)/(xmax-xmin)

(10)

式中x為目標函數值;xmax和xmin分別為目標函數的最大值和最小值;y為歸一化后的目標函數值。

F1=min{C′T-η′}

(11)

式中C′T為歸一化的投資成本;η′為歸一化的光伏滲透率。

1)投資成本。

(12)

式中r為貼現率;n為分布式光伏和儲能設備的使用年限;cPV為單位容量分布式光伏投資成本;cESS為單位容量儲能投資成本;PPV為分布式光伏總裝機容量;PESS為儲能總裝機容量。

2)光伏滲透率。

(13)

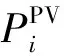
2.1.2 約束條件

1)分布式光伏接入節點數量限制。

(14)

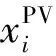
2)儲能接入節點數量限制。

(15)

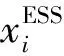
3)潮流約束。

(16)

式中Pi為節點i的有功功率;Qi為節點i的無功功率;Ui和Uj分別為節點i,j處的電壓;Gij和Bij分別為支路ij的電導和電納;θij為節點i,j的相角差;N為節點總數。

4)節點電壓約束。

(17)

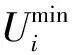
5)支路功率約束。

(18)

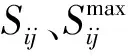
2.2 運行層模型

2.2.1 目標函數

與規劃層類似,由于目標函數量綱不同,因此同樣需要對其進行歸一化處理。

F2=min{C′y+C′loss+C′buy+VDI′}

(19)

式中C′y為歸一化的運維成本;C′loss為歸一化的網損成本;C′buy為歸一化的購電成本;VDI′為歸一化的電壓偏移指數。

1)運維成本。

(20)

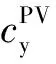
2)網損成本。

網損成本表征電能傳輸過程中產生的有功損耗費用,用于衡量配電網的能源利用效率與經濟性。

(21)

式中closs為單位網損成本;Nl為線路總數;Il,t為概率潮流所得第l條線路第t時刻的電流;Rl為第l條線路電阻。

3)購電成本。

(22)

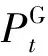
4)電壓偏移指數。

電壓偏移指數表征某一時間斷面下,配電網中節點電壓的實際值偏離額定值的程度,用于衡量配電網的電壓穩定性。電壓偏移指數越大,電壓穩定性越差。

(23)

式中Ui,t為概率潮流所得t時刻節點i電壓實際值;Ui,N為t時刻節點i電壓額定值。

2.2.2 約束條件

1)潮流約束。

(24)

式中Pi為節點i的有功功率;Qi為節點i的無功功率;Ui和Uj分別為節點i,j處的電壓;Gij和Bij分別為支路ij的電導和電納;θij為節點i,j的相角差;N為節點總數。

2)節點電壓約束。

(25)

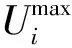
3)支路功率約束。

(26)

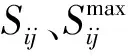
4)分布式光伏出力約束。

(27)

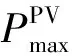
5)儲能充放電功率約束。

(28)

(29)

6)儲能SOC上下限約束。

SOCmin≤SOCi,t≤SOCmax

(30)

式中SOCi,t為第i臺儲能第t時段的荷電狀態(state of charge,SOC);SOCmax和SOCmin分別為儲能SOC上下限。

3 模型求解

3.1 求解算法

上文所提概率規劃模型為混合整數非線性規劃問題,采用傳統解析方法求解難度較大,因此文章采用改進的PSO算法求解所提模型。

PSO算法將優化問題的解視為粒子在空間中的位置[24],通過粒子個體之間的協作和競爭,在復雜的搜索空間中找到最優解,具體步驟如下:

1)初始化粒子群,根據設定參數生成初始化的粒子并隨機生成每個粒子的位置和速度;

2)迭代更新粒子群,每個粒子根據當前速度、位置、個體最優解和群體最優解,更新速度和位置,在這個過程中,粒子不斷在空間中搜索適應度更優的位置,并得到當前最優解;

3)判斷是否達到終止條件,若滿足終止條件,則輸出粒子群中最佳的粒子位置和對應的最佳適應度作為優化問題的解和目標函數的最小值;否則轉步驟2)。

在PSO算法中,慣性權重ω對算法的尋優性能有較大影響。較大的ω有利于增強全局搜索能力;較小的ω則有利于增強局部搜索能力[25]。為提升PSO算法收斂能力,本文采用線性下降慣性權重的改進方法:

(31)

式中tmax為最大迭代次數;ωmax和ωmin分別為ω的上下限,文章設為0.9和0.4。

計算過程中,ω將隨著迭代次數的增加而逐漸減小。計算初期算法具有較強的全局搜索能力,避免較早的收斂于局部最優;計算后期算法具有較強的局部搜索能力,從而提高算法的尋優性能。

3.2 求解步驟

文章所述雙層概率規劃模型求解流程如圖2所示,具體步驟如下:

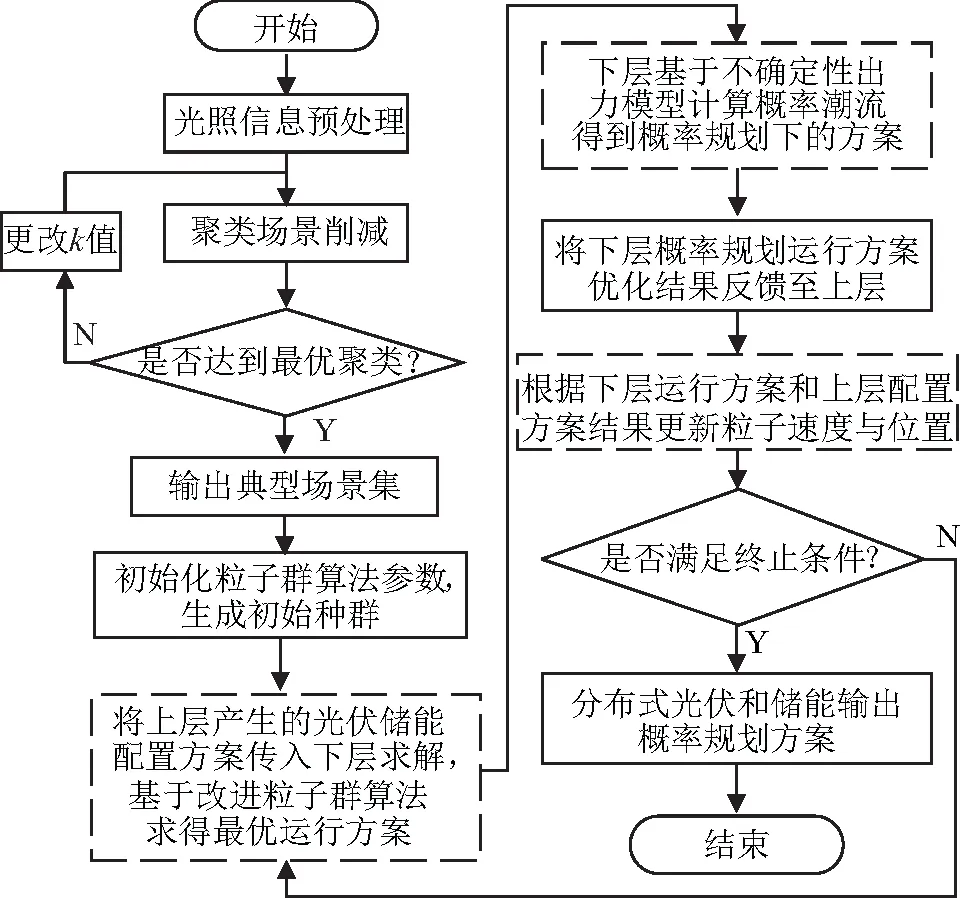
圖2 概率規劃求解流程圖

1)對光照信息進行預處理,根據肘部法確定最優聚類數目,并基于K-means聚類方法對光伏出力數據進行場景削減,生成有代表性的光伏出力概率場景集;

2)初始化粒子群算法參數,生成初始種群;

3)將上層產生的光伏、儲能配置方案傳遞給下層,作為下層的初始條件,下層模型計算多次概率潮流量化光伏出力、系統網損和電壓產生的隨機波動,從而確定每個時段系統運行的最優策略;

4)將下層產生的最優運行方案傳遞給上層,上層模型基于下層優化過后的運行方案指標值更新全局粒子速度與位置;

5)判斷是否滿足終止條件。若滿足,則全局最優粒子的位置即為分布式光伏和儲能最優配置方案;若不滿足,則更新粒子的位置和速度,轉至步驟3)。

4 算例分析

4.1 算例說明

為驗證文章所提方法的有效性,選取IEEE 33節點算例進行仿真分析。其中,IEEE 33配電網拓撲如圖3所示。

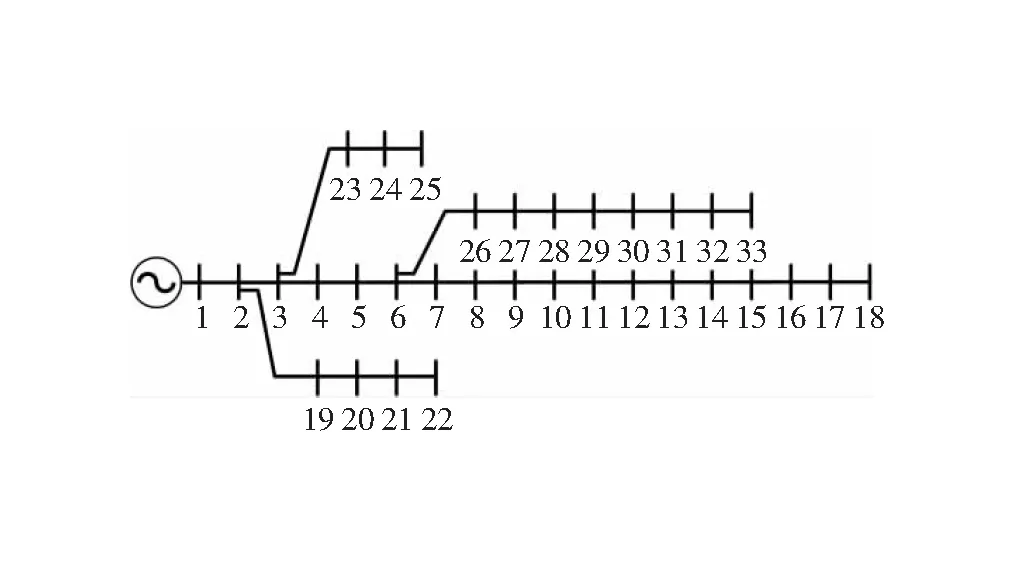
圖3 IEEE 33節點配電網拓撲圖

配電網日內負荷分布情況如圖4所示,由圖4的節點負荷功率分布可見,負荷功率于節點24～33之間達到高峰,其次是節點7～14之間,而其他節點負荷功率相對較低,由此可得,負荷主要集中于以上兩個節點區間;分布式光伏和儲能的使用年限設置為10年,光伏滲透率最高不超過70%;基于安徽某地實際光伏數據生成光伏不確定性場景,并利用肘部法確定k=4時聚類效果最佳,所得典型場景出力如圖5所示。

圖4 日內負荷分布情況

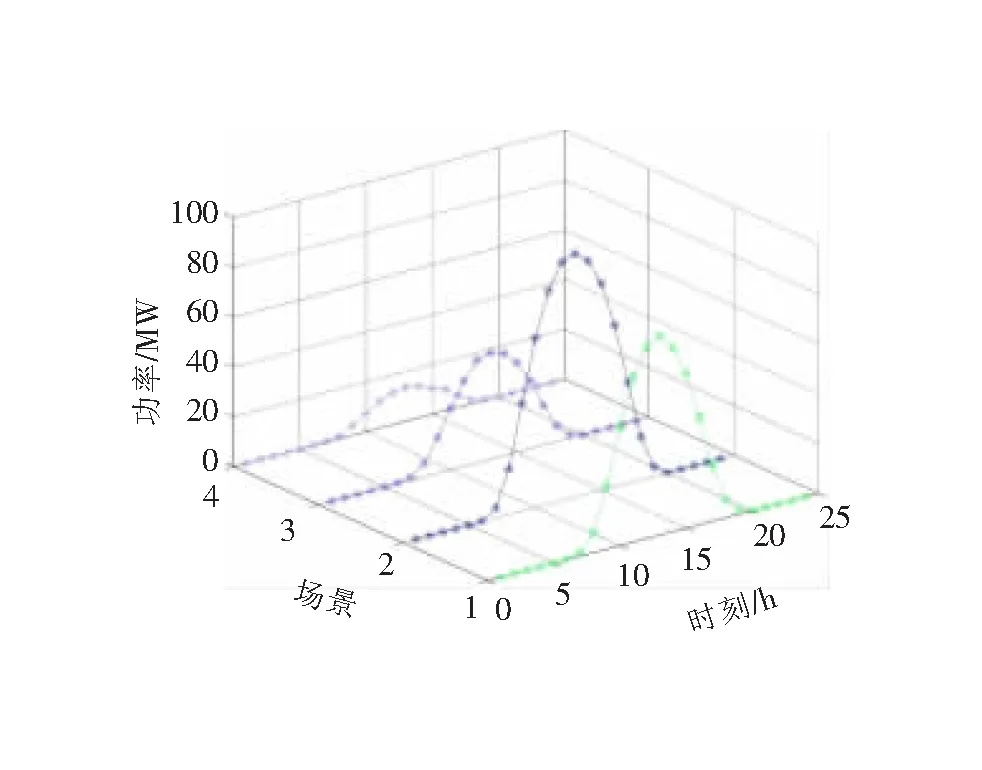
圖5 分布式光伏典型場景出力圖

設備參數如表1所示,單位容量光伏投資成本、單位容量儲能投資成本以及其余參數如表2所示。

表1 設備參數

表2 系統規劃的相關參數

4.2 算例結果

4.2.1 規劃結果分析

基于文章提出的雙層概率規劃模型進行優化配置,所得日內運行結果如圖6所示,優化配置結果如圖7所示。

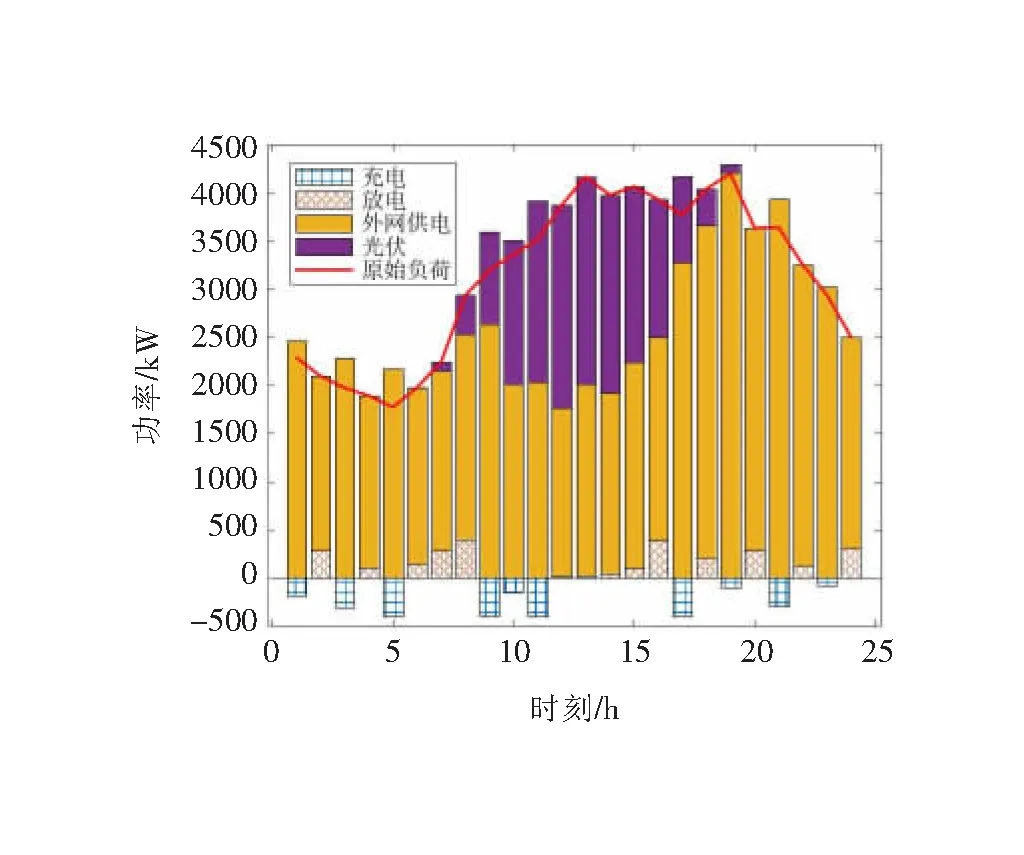
圖6 優化后配電網日內功率圖

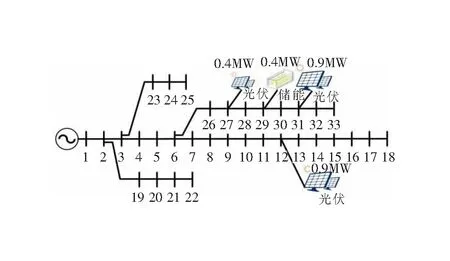
圖7 優化配置結果

綜合圖6、圖7得:考慮光伏不確定性時,分布式光伏主要安裝于負荷較為集中的支路,符合分布式光伏的就近消納原則,同時,12時前后的光伏出力高峰與負荷高峰疊加,減少了外部購電需求,有效提高了光伏利用效率;對于儲能而言,考慮光伏不確定性后,儲能設備將配置于分布式光伏較為集中的區域,并在9—11時、18—20時等時段通過充放電實現削峰填谷,從而有效平衡光伏出力波動,提高光伏消納率,有利于提升配電網穩定性。

4.2.2 指標對比分析

為驗證文章所提方法的有效性和優越性,設置了以下場景進行仿真對比:

1)場景1:不考慮光伏滲透率的配電網確定性規劃;

2)場景2:考慮光伏滲透率的配電網確定性規劃;

3)場景3(文章所提方法):考慮光伏滲透率的配電網概率規劃。

仿真所得各場景分布式光伏配置容量對比結果如圖8所示。

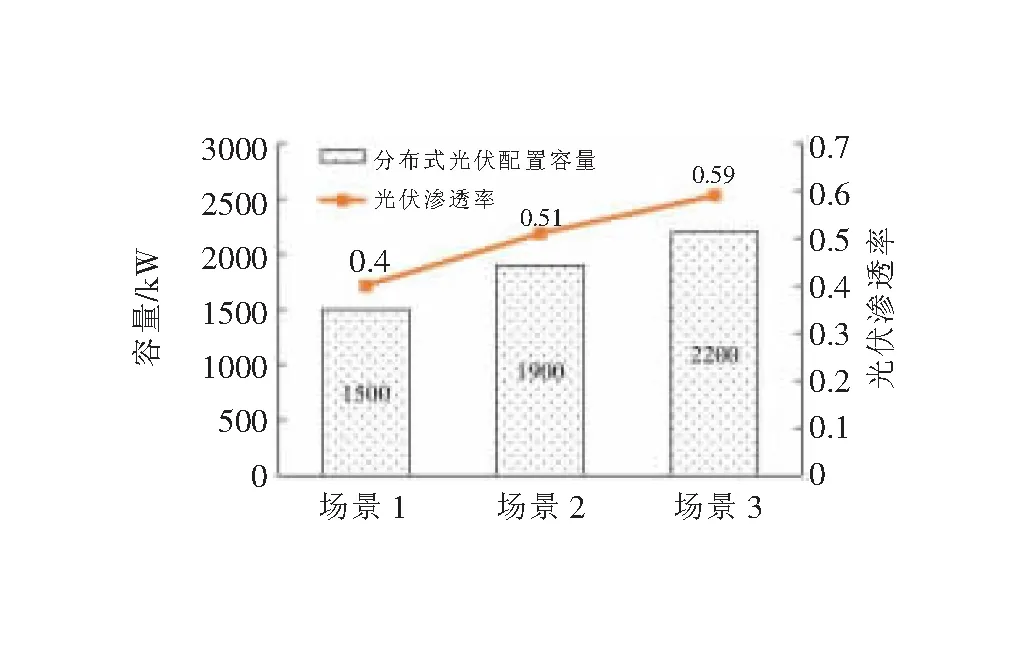
圖8 分布式光伏配置容量對比結果

由圖8得:場景3分布式光伏配置容量最高,相比場景1光伏配置容量增加700 kW,光伏滲透率提高47.50%;相比場景2光伏配置容量增加300 kW,光伏滲透率提高15.69%。表明通過考慮分布式光伏的不確定性進行分布式光伏優化配置有利于提高分布式光伏接入容量,挖掘分布式光伏并網潛力。

各場景優化配置指標對比結果如圖9所示。

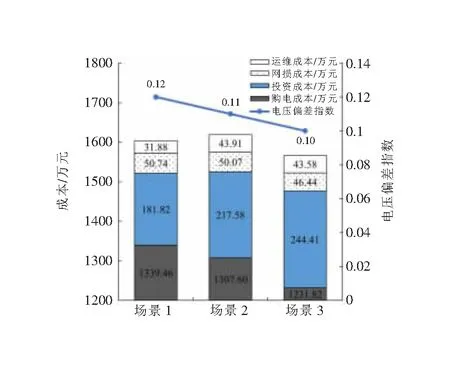
圖9 優化配置指標對比結果

由圖9得,相比場景1、場景2,場景3的購電成本分別降低107.64萬元、75.78萬元,網損成本分別降低4.30萬元、3.63萬元,電壓偏差指數分別降低了16.67%和9.09%。這是因為傳統方法基于確定性光伏出力進行規劃,應對光伏出力波動的能力較弱,難以有效消納剩余光伏出力,導致配電網在光伏發電低谷時段頻繁向外部購電,傳輸損耗增大;而所提方法基于不確定性光伏出力進行光伏、儲能規劃,在提高光伏滲透率的同時,將分布式光伏配置在系統內負荷較為集中的支路,并對分布式光伏并網出力進行優化,提供電壓與功率支撐,能夠有效提升源荷匹配程度,降低外部購電量和網損,提高規劃的經濟性、可靠性。

4.2.3 網損對比分析

不同場景下的網損分布對比結果如圖10所示。由圖10得,相比場景1、場景2,場景3網損分別降低了8.47%、7.25%。這是因為傳統方法根據確定性場景進行規劃,獲得的光伏、儲能運行方案較為單一,難以適應多變的實際光伏運行情況。場景1缺乏對光伏滲透率的考慮,光伏接入量較小,令系統在重負荷時段難以形成有效的功率支撐,外部購電量較高,增加了傳輸損耗;場景2中難以良好消納分布式光伏出力,引起系統內功率倒送,導致網損升高。由場景3結果可見,所提方法能夠模擬光伏實際運行情況,在提升光伏接入量的同時優化光伏、儲能運行方案,降低外部購電量并減少功率倒送現象,從而降低網損。

圖10 網損對比結果

5 結束語

針對分布式光伏出力不確定性對配電網規劃運行造成的經濟性、穩定性挑戰,文章提出了一種含高比例分布式光伏的配電網多目標概率規劃方法,多場景算例對比表明,所提方法具有如下優勢:

1)相較于傳統規劃方法,所提方法通過模擬光伏實際運行情況,有效挖掘分布式光伏并網潛力,提高光伏滲透率47.50%;

2)相較于傳統規劃方法,所提方法通過靈活優化光伏、儲能運行方案,能夠有效消納光伏出力,在提升光伏接入量的同時減少了功率倒送現象,從而降低網損;

3)所提方法綜合考慮光伏滲透率、經濟性與穩定性目標,電壓穩定性提高16.67%,綜合成本降低37.65萬元,兼顧了規劃的經濟性與穩定性。

在未來的研究中,將進一步研究不同種類分布式發電單元間的相關性對規劃結果的影響,實現分布式能源和儲能設備的相關性優化配置,以促進分布式能源消納。