靈動的數學條件
肖文軒
解決一個數學問題,其思考方式大致分為按條件思考或者依結論倒推。當兩者在思維上碰撞時,那么問題就迎刃而解了。
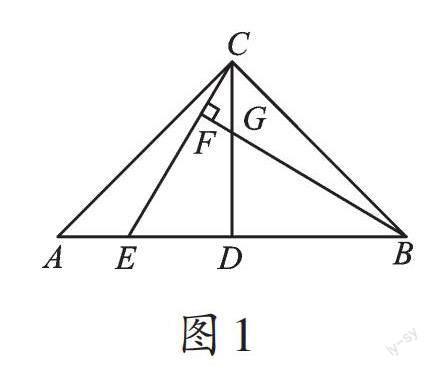
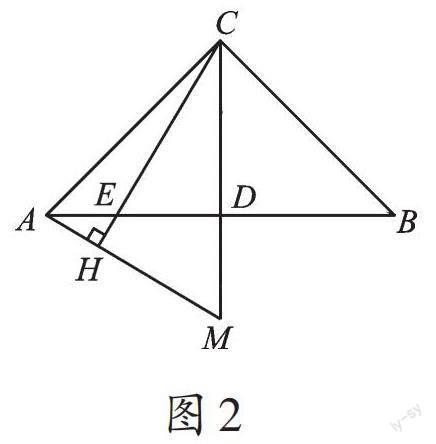
例題 在△[ABC]中,已知[AC]=BC,[∠ACB][=90°],點[D]是[AB]的中點,點[E]是邊[AB]上一點,連接CE。
(1)直線[BF]垂直于[CE],垂足為點[F],交[CD]于點[G](如圖1),求證:[AE]=[CG];
(2)直線[AH]垂直于[CE]的延長線,垂足為點[H],交[CD]的延長線于點[M](如圖2),找出圖中與[BE]相等的線段,并加以證明。
按照做題思路,我們先分析條件:①[AC]=[BC];②[∠ACB]=[90°];③點[D]是[AB]的中點。一共有三個條件,單個條件能得到一些結論,兩兩結合能得出更奇妙的結論。例如,①②結合,可得[∠CAB]=[∠CBA]= [45°]……
問題(1),提供了條件④[BF][⊥][CE],②④結合可得[∠ACE]=[∠CBF]。以上都是根據條件向下推理得出的。依據結論[AE]=[CG],說明要證明△CAE[?]△[BCG],再根據條件得出的結論,兩者在此“勝利會師”,問題得解。
問題(2)首先要進行數學猜想:[BE]=[CM],從而要證明△[CBE][?]△[ACM]。我發現,還缺少相等的條件,由條件⑤[AH⊥CH],同樣和②結合,得出[∠CAH]=[∠BCE],思維的結合點在這里,題目得到完美解決。
對于難度較高的題目,我們要形成一種好的思維習慣。首先通過題目,理解每一句,獨自推理每一句的幾何語言,然后幾個條件一起進行推理,推斷出一些相應的結論,再從結論出發反推,最后形成一連串合理的推斷。
教師點評:
小作者通過自身的解題過程,總結出自己的解題思路,形成了解決幾何問題的思想方法,充分地利用條件、分析條件,進行合理的推斷,再從結論反推,架起解決問題的“橋梁”。小作者勤于思考、反思、總結,形成解題體系,這是我們提高思維水平的重要途徑。
(指導教師:蔣小飛)

