基于GA算法優(yōu)化Stacking集成學習的金屬材料大氣腐蝕速率研究

田 輝，樊志彬，王 倩，米春旭

（國網山東省電力公司電力科學研究院，山東 濟南 250003）

0 引言

電網系統(tǒng)在人民日常生活以及社會經濟活動中擔負著舉足輕重的作用，電網設備穩(wěn)定運行是保證供電的基礎。電網設備中的金屬材料易受大氣腐蝕的影響，眾多研究發(fā)現腐蝕對設備自身穩(wěn)定性和服役性能均有較大影響，易造成較大經濟損失和安全隱患［1-2］。準確了解電網設備金屬材料的腐蝕情況是保障電網供電安全穩(wěn)定的關鍵，因此需要對電網設備金屬材料進行腐蝕預測，保證能夠提前了解設備的腐蝕情況，以便及時維護。

大氣腐蝕是一個復雜的過程，許多金屬材料的腐蝕規(guī)律仍不能被準確掌握，其往往受相對濕度、溫度、污染物等多種環(huán)境因素的影響，目前還沒有準確合理的腐蝕預測模型。因此，研究各種大氣環(huán)境下腐蝕的影響因素和腐蝕過程的動力學規(guī)律，對預測腐蝕損失具有重要意義。為了得到準確的模型來估計不同環(huán)境條件下的腐蝕規(guī)律，一些學者已經做了許多工作。

環(huán)境因子對腐蝕速率影響定量關系的研究模型主要包括劑量響應方程模型和機器學習模型等。其中，劑量響應方程模型是基于現場暴露腐蝕試驗結果與試驗點環(huán)境參數回歸分析的經驗公式。大量研究表明，金屬材料的大氣腐蝕過程同時受到多種環(huán)境因子的影響，許多研究已經得出包括溫度、濕度、潤濕時間、SO2沉積量、Cl-沉積量以及污染物等是影響腐蝕的主要因素，并分析了各自對金屬材料腐蝕速率的影響［3-5］。因此現有大多數研究也是基于上述因素建立劑量響應方程。最常用的劑量響應方程的基本形式遵循簡單的線性或對數線性關系［6］。葉堤等［7］結合灰色關聯分析和非線性回歸方法，同時考慮了氮元素的影響，建立了基于大氣腐蝕機理的碳鋼、Zn、Cu 的腐蝕劑量響應方程。李牧錚等［8］通過建立各自的和綜合的多元線性回歸方程組，除了考慮氮元素外，還考慮了大氣沉降物中水溶性降塵量，給出了金屬材料的大氣腐蝕預測劑量響應方程。

由于腐蝕數據的不確定性大，以及傳統(tǒng)回歸方法在處理非線性交互效應方面的局限性，依賴經驗公式會得到不同的劑量響應方程，這樣會產生各種各樣的公式，不利于推廣。同時，影響腐蝕速率的因素較多，依靠劑量響應方程不能綜合考慮各種環(huán)境因子的相互影響。

近幾年，基于機器學習的方法在腐蝕研究中得到了越來越廣泛的應用。機器學習模型可通過在經驗和數據中學習，自動搜索知識，而不依賴于預先確定的方程，能更好地理解和預測大氣腐蝕。人工神經網絡（artificial neural network，ANN）［9］、隨機森林（random forest，RF）［10］、支持向量機（support vector regression，SVR）［11］等算法已經應用在各類數據挖掘中。在腐蝕預測方向上也有了一些研究，其中Cai等［12］研究了相對濕度、溫度、二氧化硫和氯化物對動態(tài)環(huán)境中短期腐蝕行為的影響，提出了一種描述環(huán)境因子統(tǒng)計分布的多參數方法。Zhi 等［13］結合RF 系數和Spearman 系數的混合方法，降低了維度，給出了不同服役周期下影響腐蝕速率主要的環(huán)境因子，建立了SVR 腐蝕預測模型。Pei 等［14］改進了RF 模型，提高了對碳鋼大氣腐蝕的預測精度，且預測能力明顯強于ANN 和SVR 模型。以往研究中使用的機器學習模型往往是1～2 種模型，容易造成過擬合或者欠擬合現象，并沒有充分發(fā)揮各個模型的優(yōu)勢，因此基于機器學習的腐蝕預測還有很大的研究空間。

研究分析影響腐蝕的環(huán)境因子，并將遺傳算法和Stacking 集成學習模型結合，建立腐蝕預測模型。相較于以往的腐蝕預測模型，該模型能夠充分發(fā)揮各個機器學習模型的優(yōu)勢，在提升擬合度的同時，有效減少過擬合現象，提高模型的適用性。同時，通過較少的環(huán)境因子，更加便捷有效地對腐蝕速率進行預測，減少因采集過多環(huán)境因子帶來的工作量。

1 Stacking集成學習模型原理

Stacking 集成學習算法一般分為兩層，第一層為初級學習器，第二層為次級學習器。原始數據集經過初級學習器訓練得到一個新的數據集，用來訓練次級學習器，并最終得到預測結果［15］。該方法在訓練過程中，通過不同算法模型的優(yōu)化組合，發(fā)揮各自的優(yōu)勢，從而提高整個模型的預測準確率。其結構如圖1 所示。

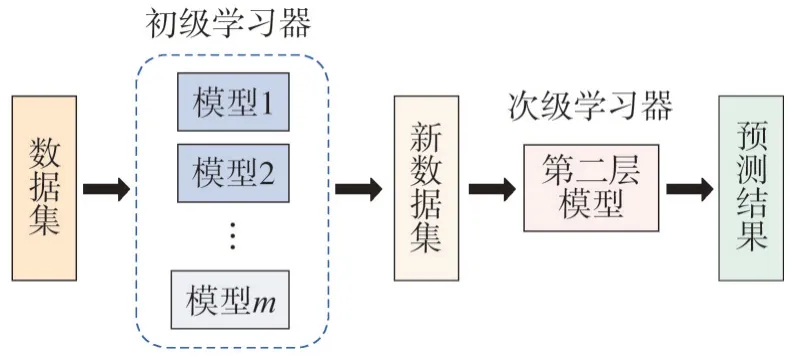
圖1 Stacking算法示意Fig.1 Schematic of stacking algorithm

首先，將數據分為訓練集Tr和測試集Te，為進一步降低過擬合，訓練集Tr又被分成K份：｛Tr1，Tr2，…，TrK｝。在第一層初級學習器中，取其中K-1份作為訓練集，另外一份作為驗證集，每個模型分別進行K次訓練，每次可以得到一個驗證集預測結果V和一個預測集結果P，分別表示為｛V1，V2，…，VK｝、｛P1，P2，…，PK｝。經過m個模型訓練則可以得到m組訓練集預測結果，驗證集預測結果為｛V11，V12，…，V1K，V21，V22，…，V2K，…，Vm1，Vm2，…，VmK｝，預測集結果為｛P11，P12，…，P1K，P21，P22，…，P2K，…，Pm1，Pm2，…，PmK｝。同時，對K次訓練得到的預測集結果求平均值得到m組測試集預測結果：｛P1，P2，…，Pm｝。由第一層訓練集預測結果和測試集預測結果組成第二層次級學習器的輸入，實現對第一層初級訓練器結果優(yōu)化，提高預測的準確性。

1.1 初級學習器

對于初級學習器，用到的算法包括隨機森林算法、自適應增強算法（adaptive boosting，AdaBoost）、梯度提升決策樹算法（gradient boosted decision trees，GBDT）和極端梯度提升算法（extreme gradient boosting，XGBoost）。

1）隨機森林算法。

隨機森林由Breiman 等提出，是基于樹的機器學習算法，其基本單元是決策樹。它是一個集成分類器，由許多獨立的決策樹組成，并輸出大多數決策樹預測的類。算法過程如圖2 所示。

算法步驟如下：

a）將訓練數據集有放回抽取N次，得到新的子訓練集｛D1，D2，…，DN｝，作為決策樹根節(jié)點處的樣本。

b）隨機選取屬性做節(jié)點分裂屬性，并重復該步驟。

c）通過以上步驟，建立大量決策樹，形成隨機森林。

d）將每棵樹輸出的預測值求平均值得到最終預測結果。

2）AdaBoost 算法。

AdaBoost 算法是由Freund 和Schapire［16］在1995年提出，針對同一訓練集進行不同學習器（分類器）的訓練，并將這些弱學習器集合起來，組成一個更有效的強學習器。在解決回歸問題時，具體算法過程如下。

a）初始化每個樣本數據的權值分布。

假定練集樣本為

訓練集的第k個弱學習器的輸出權重為

式中：ωki(i=1,2,…,N)為第i個樣本在第k個弱學習器的輸出權重。

則初始化樣本集權重為

b）進行第k次迭代。

①使用具有權值分布Dk（k=1，2，…，K）的訓練樣本集進行學習，得到弱學習器gk。

②訓練集上的最大誤差為

式中：xi為第i個樣本；yi為xi的目標值。

③計算每個樣本的相對誤差為

④計算在gk訓練數據集上的回歸誤差率為

⑤計算弱學習器系數為

⑥更新訓練樣本集的權值分布為

c）結束K輪迭代，得到最終強學習器為

式中：gk*(x)為所有的中位數值乘以對應序號k*對應的弱學習器。

3）GBDT 算法與XGBoost 算法。

GBDT 算法由Friedman［17］提出，是一種迭代的決策樹算法，由多棵決策樹組成，所有樹的結論累加起來作為最終答案。GBDT 算法可以看成是M棵樹組成的加法模型。

式中：x為輸入樣本；υ、υm為模型參數；hm(x,υm)為分類回歸樹；δm為每棵樹的權重。

其算法過程如下。

a）初始化學習器

式中：L(?)為損失函數。

b）建立M棵分類回歸樹。

①計算第m棵樹（m=1,2,...,M）對應的響應值為

式中：F(x)為學習器函數；Fm-1(x)為第m-1 輪得到的學習器。

②用(xi,rm,i)擬合得到第m棵回歸樹Tm，葉子節(jié)點區(qū)域劃為Rm,j（j=1,2,…,Jm），Jm為第m棵回歸樹葉子節(jié)點的個數。

③遍歷所有節(jié)點，計算回歸樹Tm的每個葉子節(jié)點Rm,j的輸出值，即為最佳擬合值cm，j。

④更新學習器為

c）重復步驟直到滿足停止條件，累加得到最終的學習器表達式為

XGBoost 算法是建立在GBDT 算法上，進一步改進了算法，不再詳細展開。

1.2 次級學習器

次級學習器由人工神經網絡模型構成。人工神經網絡的節(jié)點相當于一個神經元，這些神經元接收外界的輸入信息進行計算和調整，并將它們輸送到其他神經元。神經元的計算函數由神經元輸入連接的權重定義，通過恰當地改變這些權重大小可以學習得到計算函數，對輸入數據建立相關模型。BP（back propagation，BP）神經網絡是常見的神經網絡算法，是一種基于誤差反向傳播算法的三層前饋神經網絡，主要由輸入層、隱含層和輸出層構成。BP神經網絡具有實現任何復雜非線性映射的功能，使其適合求解內部機制相對復雜的問題，其網絡結構如圖3 所示。其中輸入層、隱含層和輸出層神經元個數分別為M、I和J，Xm表示輸入層第m個神經元，Ki表示隱含層第i個神經元，Yj表示輸出層第j個神經元。

圖3 BP神經網絡Fig.3 BP neural network

隱含層和輸出層采用Tan-Sigmoid 函數作為傳遞函數

式中：n為迭代次數。

采用Levenberg-Marquardt 算法對網絡權值進行修正

式中：J為包含誤差性能函數對網絡權值一階導數的雅克比矩陣；μ為一個需要設置的常數；e(n)為網絡總誤差。

權重/閾值學習函數采用梯度下降動量法來進行權值的迭代

式中：η為學習率；β為動量因子。

2 預測模型構建

對于隨機森林、AdaBoost 算法等幾個初級學習器，需要設置決策樹最大深度和基分類器個數，依靠人工經驗選擇的方式往往效果不佳，采用遺傳算法對其優(yōu)化后得到更好的擬合效果。

遺傳算法是一種受進化和自然遺傳學原則指導的隨機搜索和優(yōu)化技術。遺傳算法由一種群體組成，其中每個個體代表搜索優(yōu)化問題的一種可能的解決方案。通過適應度函數篩選優(yōu)質個體；然后，在交叉算子的控制下產生新的個體，通過突變算子將隨機噪聲添加到后代中，以改變其“基因”。通過重復上述過程，最終提供一個較好的解決方案。

基于GA 優(yōu)化的Stacking 集成學習模型框架如圖4 所示，整個預測過程主要分數據預處理、遺傳算法優(yōu)化參數、初級學習器模型訓練、次級學習器模型訓練及模型預測。具體過程如下。

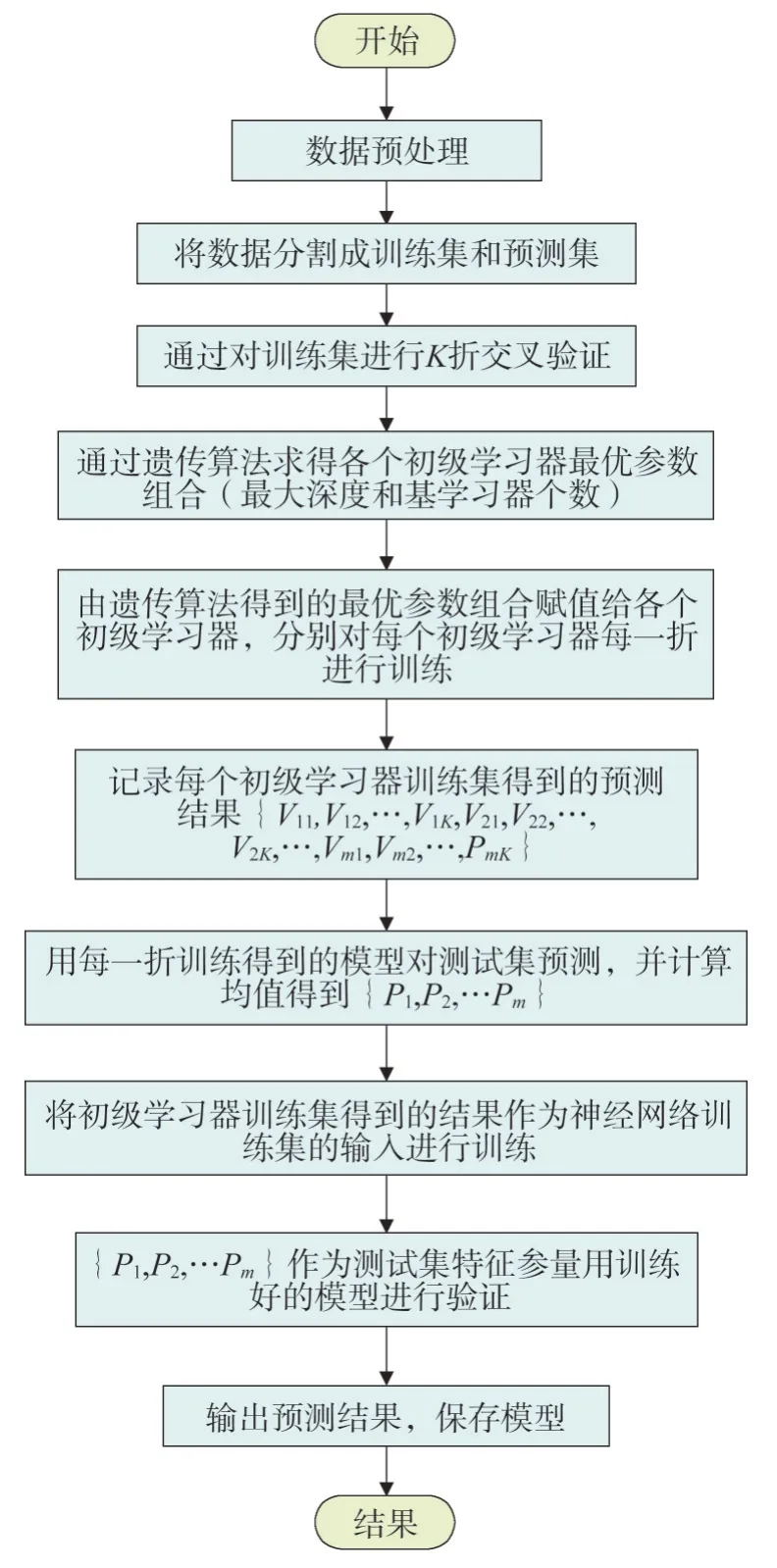
圖4 預測模型流程Fig.4 Prediction model process flow

a）數據預處理。通過對數據集進行數據的清洗，刪除掉不符合實際的數據，并對缺失部分的數據進行補齊。

b）將數據集分割成測試集和驗證集，并對測試集分成K份，進行K折交叉驗證。

使用遺傳算法求得各個初級學習器的最優(yōu)參數組合（最大深度和基學習器個數），以優(yōu)化初級學習器的模型。

c）使用初級學習器訓練得到訓練集預測結果｛V11，V12，…，V1K，V21，V22，…，V2K，…，Vm1，Vm2，…，VmK｝，以及測試集預測結果｛P1，P2，…，Pm｝。

d）將初級學習器訓練得到的結果作為新的數據集，使用次級學習器進行訓練得到最終結果。

3 模型評價指標

設計擬合優(yōu)度R2和均方根誤差RMSE兩個評價指標，其具體表達式如式（19）所示。

式中：yi為待擬合數據為擬合數據為待擬合數據均值；Sreg為回歸平方和；Sres為殘差平方和；Stot為總平方和。

4 算例分析

取用山東省28 個暴露腐蝕試驗站的鍍鋅鋼腐蝕數據對提出的模型進行驗證。結合Spearman 相關系數和隨機森林特征重要性評估的方法，分析了多個環(huán)境因子與腐蝕速率的相關性，結果如表1 所示。

表1 環(huán)境因子與鍍鋅鋼腐蝕速率的相關性Table 1 Correlation between environmental factors and corrosion rate of galvanized steel

通過表1 可以得出，潤濕時間和Cl-沉積量對鍍鋅鋼腐蝕速率的影響較大。結合以往研究和本文的分析將溫度、濕度、潤濕時間、SO2沉積量和Cl-沉積量這幾個主要環(huán)境因子作為模型的輸入來進行訓練。

將28 條站點數據中的23 條數據作為訓練集，5條作為測試集。利用Python 編寫基于GA 優(yōu)化的Stacking 集成學習模型。遺傳算法模型的初始種群個數設置為20 個，交叉率為40%，變異率為66.6%，迭代20 次，求得隨機森林、Adaboost、GBDT 和XGBoost 初級學習器的最大深度和基分類器個數分別為（16，174）、（20，109）、（11，11）和（7，156）。

人工神經網絡的隱含層節(jié)點數設置為10，學習速率為0.015。迭代次數設為25000 次。經過次級學習器的訓練，得到28 站鍍鋅鋼腐蝕速率實際值和預測值如表2 所示，測試集在不同模型下的預測結果擬合優(yōu)度R2和均方誤差RMSE如表3 所示。

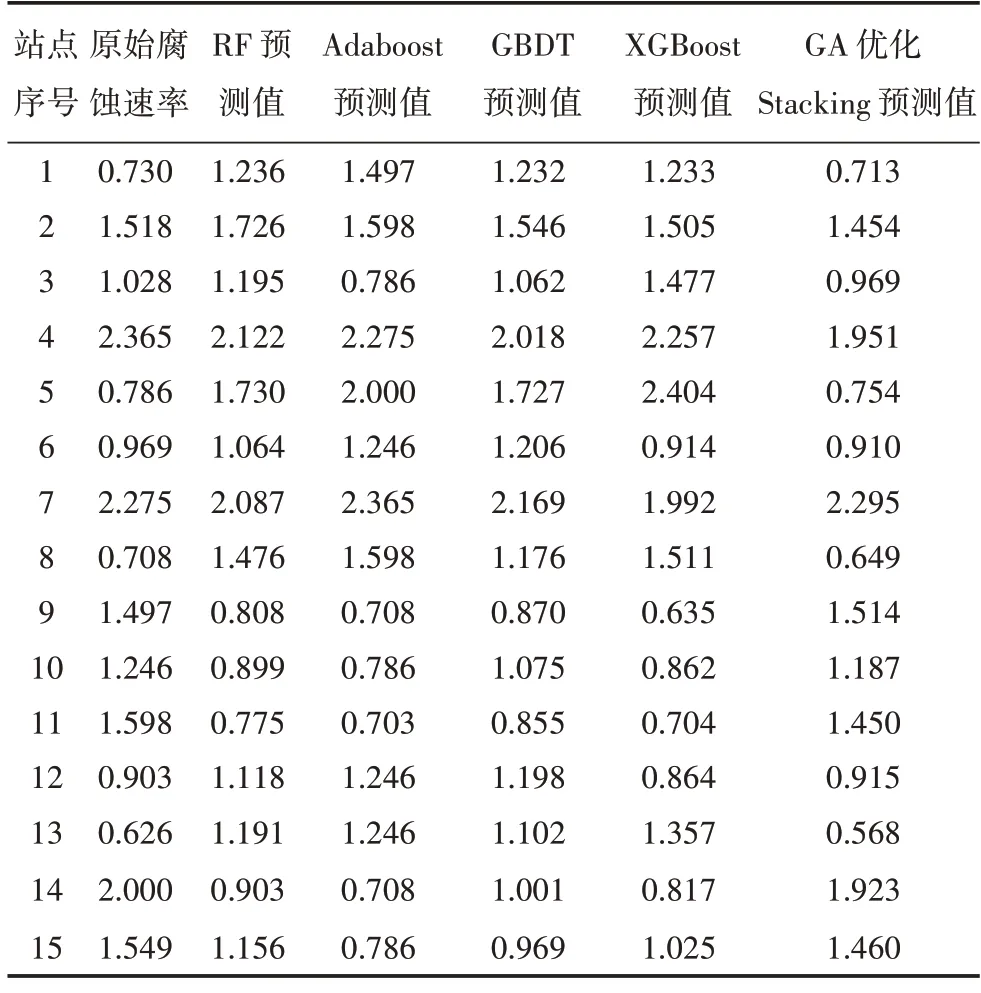
表2 鍍鋅鋼腐蝕速率實際值和預測值Table 2 Actual and predicted values of corrosion rate of galvanized steel 單位：μm/a

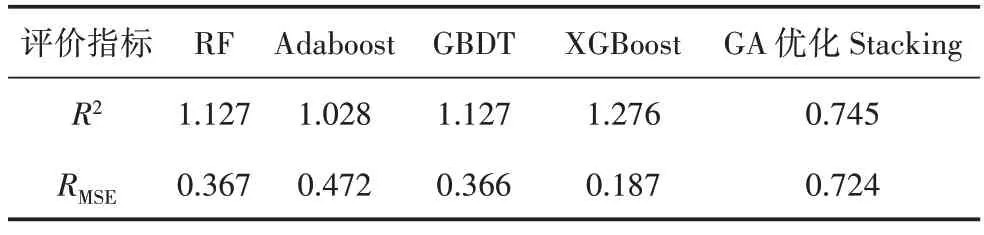
表3 不同模型預測結果的評價指標Table 3 Evaluation indexes of prediction results of different models

結合表1、表2 和表3 可以得出，在模型中減少了PM2.5、PM10、NO2、O3等環(huán)境因子輸入的情況下，可以實現以較少的環(huán)境因子作為模型輸入開展腐蝕速率的預測。

該模型結合了多個預測模型的優(yōu)點，可以充分發(fā)揮各個模型的作用。相較于RF、Adaboost、GBDT 和XGBoost 算法的單個模型，通過該模型第一層初級學習器和第二層次級學習器神經網絡的訓練，優(yōu)化了預測效果，提升了擬合優(yōu)度，降低了均方根誤差。

5 結束語

為了更好地擬合大氣環(huán)境與電網設備材料腐蝕的量化關系，提出一種基于GA 優(yōu)化的Stacking 集成學習預測模型。利用該模型對山東省28 個暴露腐蝕試驗站的環(huán)境與鍍鋅鋼腐蝕數據進行訓練，相較于常規(guī)的機器學習模型，可以在使用較少的環(huán)境因子的情況下實現對電網設備金屬材料腐蝕速率的預測；在降低過擬合的同時擬合優(yōu)度得到進一步提升，均方根誤差得到進一步減小，能更有效地實現鍍鋅鋼腐蝕速率的預測。使用文中提出的模型可以進一步地指導電網設備的部署和防護，降低因腐蝕老化造成的經濟影響，具有一定的實用性和推廣價值。文中使用的數據量有限，將來會繼續(xù)收集實驗數據以優(yōu)化模型，同時將暴露周期因素考慮在內，構建長期腐蝕速率模型。