基于改進麻雀搜索算法的受端電網機組組合模型
劉文學,王明強,房 俏,蔣 哲,梁正堂
(1.國網山東省電力公司電力科學研究院,山東 濟南 250003;2.山東大學電氣工程學院,山東 濟南,250061)
0 引言
世界上很多國家(如中國、巴西等)的能源資源(煤炭、風能資源、太陽能資源、水力資源)集中地區與負荷需求地區存在逆向分布,需要大規模、遠距離、高效率的電力傳輸技術。特高壓直流輸電在這方面具有天然的優勢,因此成為解決能源逆向分布問題的主要方式。我國已相繼建成并投運魯固、昭沂、銀東、雁淮、天中等跨區域特高壓直流輸電工程,使得電網形成交直流混聯大電網的格局[1-4]。
同時負荷中心大多數分布在經濟發達地區,即沿海地區,風電等新能源發電資源豐富,受到國家政策的大力支持。在《可再生能源法》的激勵下,我國的風電裝機容量已達2.14 億kW。然而,風速固有的間歇性和波動性使得風力發電預測存在大量的誤差,從而給電網運行帶來很大的影響[5-9]。
受端電網的機組組合優化是指滿足常規火電機組和系統相關約束的情況下,通過制定火電機組的啟停計劃和出力計劃以及直流輸送功率,最小化系統的運行成本[10]。經過電力工作者多年的研究,機組組合優化無論在建模還是求解方法上都積累了很多的成果[11-13]。文獻[14]對新能源發電接入電網后的動態經濟調度以及機組組合問題進行研究,并利用概率表示風電的不確定性。文獻[15]研究考慮火電機組閥點負荷特性的含風電的動態經濟調度模型,以約束的方式處理風電,并利用量子遺傳算法求解。文獻[16]在考慮連鎖故障風險的交直流容量最優分配問題基礎上,進行交直流容量最優分配問題的初步分析和數學建模。文獻[17]綜合分析直流閉鎖后電網一次調頻容量以及二次調頻后節點電壓、線路功率等電網運行結果,并以此為約束條件建立一種考慮直流饋入的新型受端電網機組組合模型,能夠確保受端電網直流閉鎖后的頻率、電壓和線路功率都在正常范圍內。
現有文獻都沒有同時考慮直流饋入和新能源發電出力的影響[17],因此在上述文獻的研究基礎上,建立同時考慮直流饋入和風電不確定性的新型受端電網的機組組合數學模型,并提出利用改進的新型麻雀搜索法對模型進行求解,從而得到受端電網的開停機以及運行功率。通過改進后的10 機39 節點測試系統算例驗證所提模型和算法的可行性和有效性。
1 受端電網機組組合模型
1.1 目標函數
受端電網大部分集中在沿海,不存在大量水力發電這一特殊情況,因此模型優化目標中主要包括火電機組發電成本、火電機組啟停成本、直流運行維護成本,構建的目標函數為
式中:NT為機組組合調度周期;NG為受端電網可調度機組數;PGit為火電機組i在t運行周期內的計劃出力;Iit為火電機組i在t運行周期內的開停機狀態,取值為1 表示開機狀態,取值為0 表示停機狀態;Ci(?)為火電機組i的燃料費用函數;Sit為火電機組i在t運行周期內的開機成本;PDt為饋入直流在t運行周期內輸送功率;D(?)直流運行維護成本費用函數。
火電機組燃料費用函數Ci一般為機組出力PGit的二次函數,如式(2)所示。
式中:ci、bi和ai為火電機組i的燃料費用系數。
火電機組開機成本Sit與機組的鍋爐溫度有著密切關系,如果長時間停機導致鍋爐冷卻,從而增加機組的開機成本。Sit的函數表達式為
式中:HCi和CCi分別為火電機組i熱、冷開機費用;MDi為火電機組i最小停機時間;CSTi為火電機組i冷開機時間;OTit為火電機組i在t運行周期停機時間。
因為直流送端電網的電力資源往往為水力發電或者光伏、風電等新能源發電,通常發電成本基本為零,本模型只考慮直流的運行維護成本,為簡化模型統一采用線性模型,如式(4)所示。
式中:bD為直流輸電輸送單位功率時的運行費用。
1.2 運行時約束
1)火電機組出力約束。
火電機組出力約束如式(5)所示。
式中:PGimin、PGimax分別為火電機組i的最小出力和最大出力。
2)直流輸送功率上下限約束。
直流輸送功率上下限約束如式(6)所示。
式中:PDmin、PDmax分別為直流輸送功率的最小值、最大值。
3)備用容量約束。
備用容量約束如式(7)和式(8)所示。
式中:rui和rdi分別為火電機組i的上、下爬坡率;T10為火電機組旋轉備用啟用的反應時間,一般為10 min。
4)機組爬坡速率約束。
機組爬坡速率約束如式(9)—式(12)所示。
5)機組最小開停機時間約束。
機組最小開停機時間約束如式(13)所示。
式中:Ton,i(t-1)和Toff,i(t-1)為火電機組i在t-1 運行周期內的持續開、停機時間;Ton,it和Toff,it分別為火電機組i在t運行周期的最小開停機時間。
6)系統功率平衡約束。
每一機組組合周期內,常規機組出力、直流輸送功率、風電出力預測值和負荷出力預測值保持功率平衡,如式(14)所示。
式中:PLt為t運行周期內負荷預測期望值;PWt為t運行周期內風電出力期望值。
7)正備用機會約束。
為了簡化模型,對風電出力和負荷采用正態分布。機組正備用能夠在一定置信水平下應對風電預測存在負誤差以及負荷預測出現正誤差等不確定性,如式(15)所示。
8)負備用機會約束。
發電機組發生強迫停運時,系統中功率缺乏,負備用的意義不明顯,其機會約束不必考慮。機組負備用能夠在一定置信水平下應對風電預測存在正誤差和負荷預測出現負誤差等不確定性,如式(16)所示。
式中:β2為概率置信水平。
2 模型求解
2.1 隨機機會約束的確定等價
運行時約束中的正、負旋轉備用約束,為隨機機會約束,存在兩種處理方法:隨機模擬檢驗和確定等價。隨機模擬檢驗,也稱為Monte Carlo 模擬,是對隨機系統模型進行反復抽樣試驗的技術,已經應用于眾多領域。由于它不是十分準確的技術,只能提供統計估計而非精確結果,研究問題時較慢且耗時較長,因此經常用于處理解析方法行不通的隨機問題。確定等價是對隨機變量概率分布比較確定的隨機機會約束,將其轉化為確定等價形式,采用這類方法可以得到原隨機機會約束的解析解。由于本文中風電出力和負荷的預測采用正態分布,采用確定等價的方法不僅能得到約束的精確解,還能降低求解難度并減少運算時間。
確定等價的方法如下:假設g(x,ξ)為隨機變量函數,由常變量x和隨機變量ξ組成;α為概率置信水平。對于隨機機會約束Pr{g(x,ξ)≤0}≥α,如果函數g(x,ξ) 的形式可以表示為g(x,ξ)=h(x)-ζ,h(x)為化簡后的函數,ζ為化簡后的隨機變量,而且隨機變量ζ的分布函數為Φ,則原機會約束的形式可以轉化為
式中:Kα為滿足α的概率置信數,Kα=sup{K|Φ-1(1-α)},sup 表示上確界,即最小上界。
2.2 改進麻雀搜索算法
麻雀搜索算法是根據麻雀的尋找食物行為和反捕食行為建立數學模型來進行尋優的智能優化算法[18]。為更好說明算法,首先對麻雀的尋食行為理想化并制定相應的規則:
1)麻雀群體分為生產者和拾荒者兩種類型。生產者是具有較高能量值的個體,同時為拾荒者提供尋食的方向,并負責判斷可以尋找到具有充足食物的區域。能量值的高低取決于個體適應度。
2)假如生產者發現存在危險,如出現危害種群的天敵,就會發出報警信號。當警報值大于安全閾值時,生產者需要帶領所有的拾荒者到安全區。
3)如果麻雀個體尋找到更好的食物,就可以成為生產者,但生產者和拾荒者在整個種群中的比例是不變的。
4)能量值較高的麻雀個體為生產者。為得到更大的能量值,饑餓的拾荒者更有可能到其他區域尋食。
5)拾荒者跟隨能量值高的生產者尋找食物來源,而同時拾荒者會時刻跟蹤生產者并爭奪食物,提高自身的生存機會。
6)處于群體四周的麻雀個體在感受到危險時快速向安全區域挪動以獲得更好的位置,而群體中的麻雀則隨機走動,以貼近其他麻雀。
在優化算法中,需要使用麻雀個體來尋找食物進行優化。麻雀個體的位置用矩陣表示,如式(18)所示。
式中:m為麻雀群體的數目;d為優化變量的個數。因此,麻雀群體的適應度表示為
式中:f為適應度函數;FX中的每一數值為麻雀個體的適應度。
在優化過程中,適應度高的生產者在優化搜索過程時優先得到食物。另外,由于生產者負責搜索食物并指引其余麻雀個體的尋食活動。因此,生產者需要在比拾荒者更寬泛的區域覓食。依據規則1)和2),在優化過程中迭代時,產生的新生產者位置如式(20)所示。
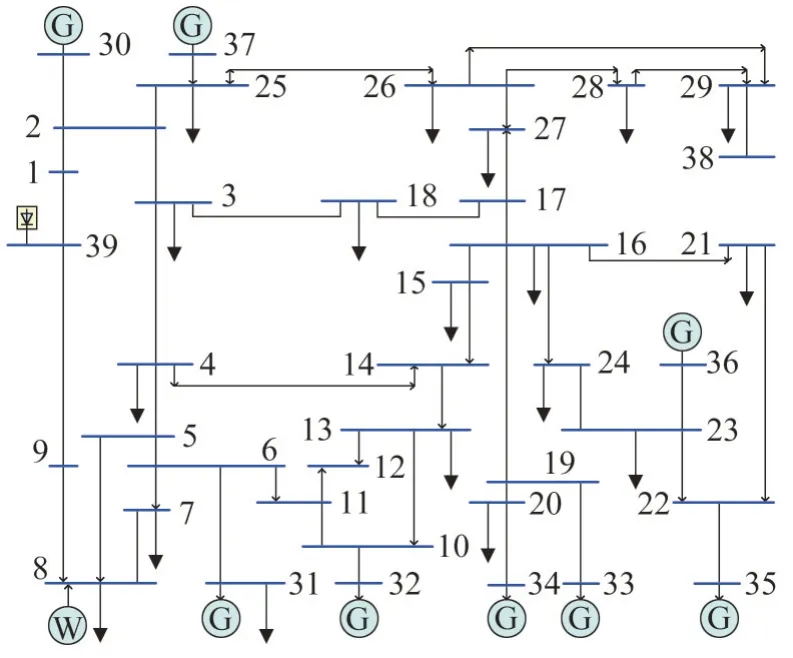
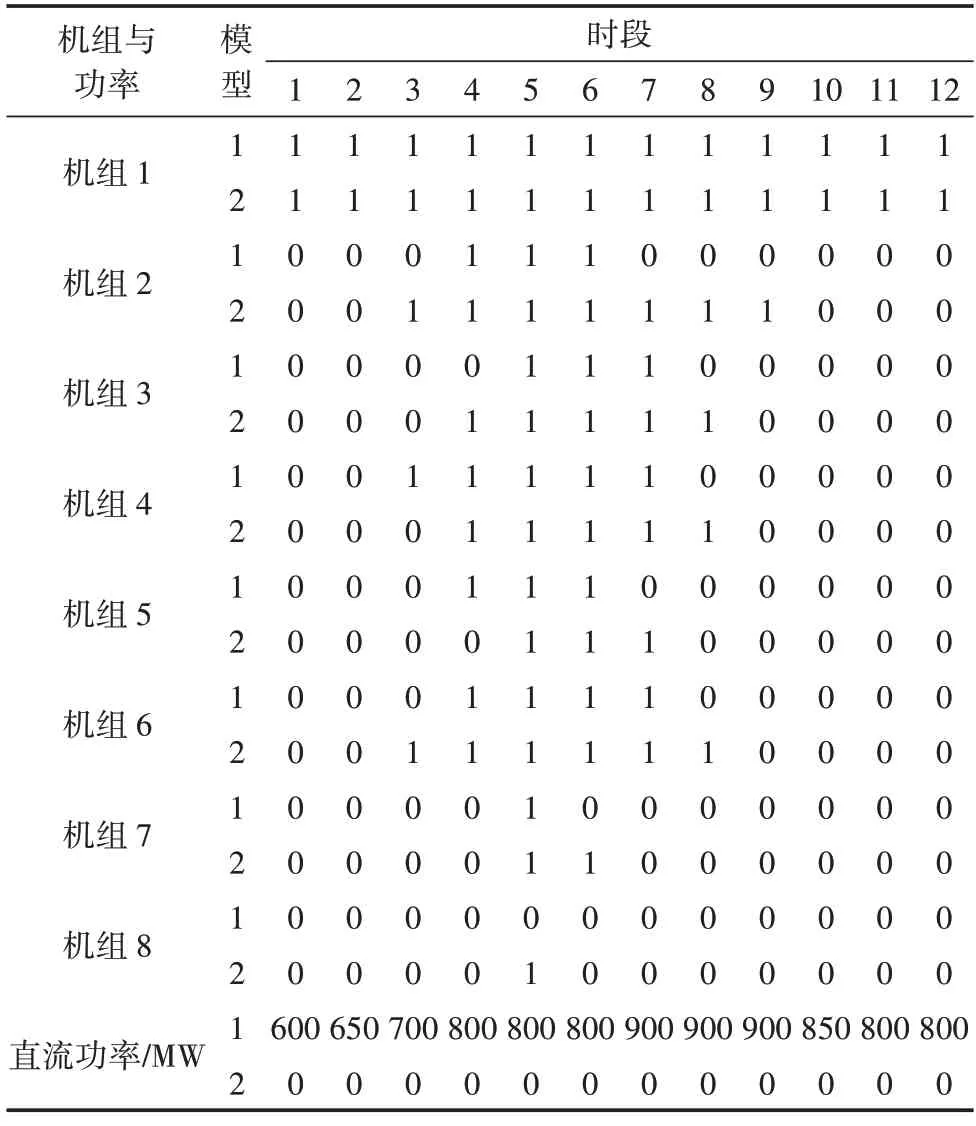
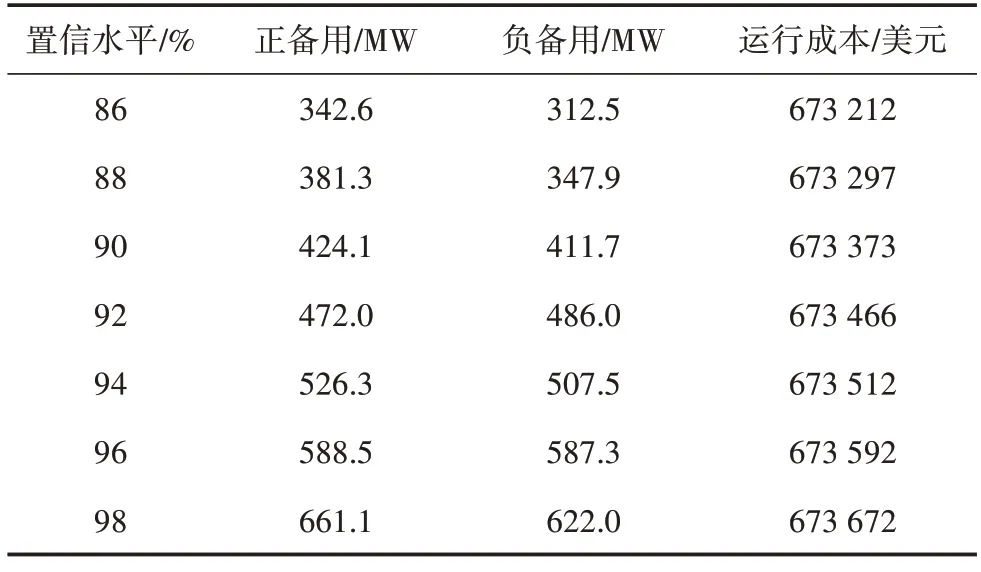
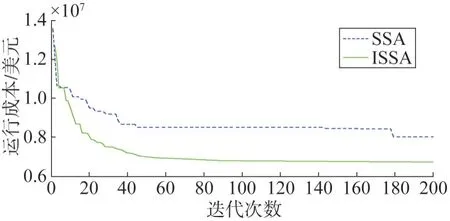
式中:k為迭代次數;kmax為最大迭代次數;l為群體中麻雀個數,l=1,2,…m;j為優化變量的維度,j=1,2,…d為第k次迭代的第l個麻雀個體的第j維的數值;α1∈(0,1]是一個隨機數;R2(R2∈[0,1])和ST(ST∈[0,1])分別是麻雀群體的報警值和安全閾值;Q為利用正態分布的隨機模擬產生的隨機數;L為1×d維度的矩陣,而且每個元素為1。當R2 拾荒者依據規則4)和規則5)產生新麻雀個體。拾荒者會經常地訪問生產者,如果發現生產者能夠找到豐富的食物,就會馬上離開現在位置去爭搶食物。一旦它們勝利,便可以立刻得到生產者的食物,否則依舊執行規則5)。因此,拾荒者的迭代公式如式(21)所示。 算法中產生新麻雀搜索個體的可調整參數中,β與K是迭代中重要的參數,較大的時候,便于麻雀個體在廣泛的區域搜索,因此有利于提高算法全局搜索能力。較小的時候,麻雀個體在較小的區域內搜索,從而增強算法的局部搜索能力。麻雀搜索算法前期需要全局搜索能力,而后期需要局部搜索能力,因此采用線性遞減權重提高搜索能力[19-20],β與K算法迭代的變化如式(23)和式(24)所示。 式中:βmax和βmin分別為變量β最大值和最小值;Kmax和Kmin分別為變量K最大值和最小值。 利用改進麻雀搜索算法求解受端電網機組組合模型的流程如圖1 所示,具體如下: 圖1 機組組合優化方法流程Fig.1 Flowchart of unit commitment optimization model 1)輸入受端電網基礎數據,包括發電機參數、風電出力和負荷的概率參數、直流輸送功率范圍以及概率置信水平。 2)確定麻雀搜索算法的參數,并設定迭代次數k=1、最大迭代次數kmax和麻雀種群規模m。 3)初始化麻雀種群的位置X以及生產者和拾荒者的比例。 4)將機會約束確定等價,利用罰函數方式處理約束,并得到麻雀個體位置的適應度f(X)。 5)對每個生產者個體利用式(20)更新麻雀個體的位置,產生生產者個體。 6)利用式(21)更新拾荒者麻雀個體。 7)利用式(22)更新警戒者麻雀個體。 8)計算新產生的麻雀個體的適應度,重排麻雀個體,并找到當前最優值。 9)判斷最大迭代次數。若k=kmax,則結束,輸出最優個體;否則轉到4)。 為驗證所提受端電網機組組合模型和改進麻雀搜索算法的有效性,以改進的10 機39 節點測試系統對組合方法進行算例測試。用同等容量的直流輸電和風電站替代典型系統的發電機組,如圖2 所示,具體參數見文獻[17]。 圖2 改進的10機39節點測試系統Fig.2 Diagram of the modified IEEE 10-unit 39-bus system 風電預測誤差和負荷預測誤差分別為預測值4%和5%。利用MATLAB 編程進行求解,最大迭代次數設置為200,種群數目設置為50。 為分析直流輸電對機組組合影響,進行兩種模型的比較:模型1,考慮直流輸送的傳統機組組合模型;模型2,不考慮直流輸送的傳統機組組合模型。 兩種模型優化得到的各個時段的機組組合啟停狀態如表1 所示,運行成本分別為673 212 美元和788 472 美元。從表1 中可以看出,受端電網考慮直流饋入時,運行成本比未考慮直流饋入稍低,由于模型2 沒有直流饋入,更多的機組處于開機狀態保證功率平衡。這也說明直流輸電能夠降低大量運行成本,反映了直流輸電的運行經濟價值。 表1 兩種模型下所求的機組開停與直流功率Table 1 Startup and shutdown status of power units and DC power in two models 表2 為不同置信水平的正備用容量、負備用容量和運行成本。從表2 中可以看出,置信水平升高,意味著系統安全水平提升,同時系統所需要的備用容量也逐漸增大,相應的運行成本增加。 表2 不同置信水平下的備用與運行成本Table 2 Reserve capacities and operating costs at different confidence levels 改進麻雀算法的收斂特性如圖3 所示,可以看出,加入線性遞減權重后,增加種群多樣性,增強算法迭代過程的前期全局搜索和后期局部尋優能力,因此得到的最優解優于普通的麻雀搜索算法。 圖3 算法的收斂特性曲線對比Fig.3 Comparison of convergence characteristic curves of algorithms 對含直流饋入和新能源大規模并入的受端電網機組組合問題進行研究。考慮到直流輸電的特性,將其作為有功源參與機組組合,并同時考慮新能源和負荷的出力不確定性,建立新型受端電網的機組組合模型,并利用改進的麻雀算法對機組組合模型進行求解。在改進的10 機39 節點測試系統上對所提方法的效果進行驗證,發現所得最優方案在減少受端電網運行成本的同時,也能適應新能源出力的不確定性。模型求解時使用改進麻雀搜索算法,提高算法的全局搜索和局部尋優能力,能夠很好解決受端電網機組組合問題。2.3 算法流程
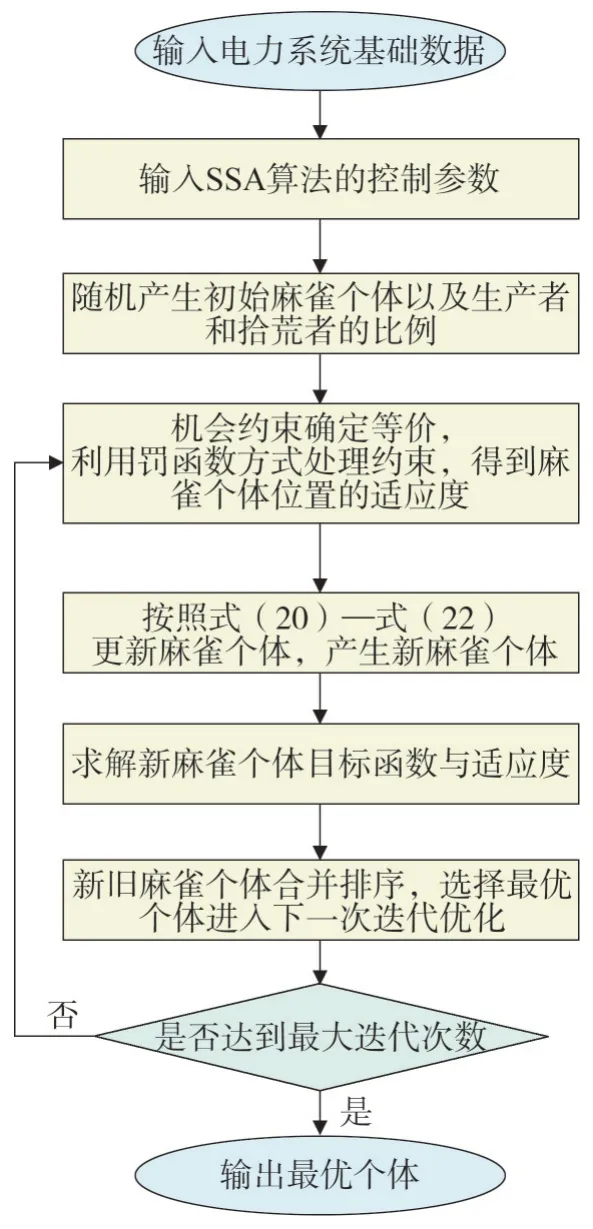
3 算例分析
4 結束語

