信息技術(shù)在高中函數(shù)教學(xué)中的應(yīng)用

【摘要】本文以教學(xué)三角函數(shù)這一典型的周期函數(shù)為例，論述將信息技術(shù)融入高中函數(shù)教學(xué)的策略：運(yùn)用信息技術(shù)將抽象的知識(shí)可視化，快速且準(zhǔn)確地呈現(xiàn)函數(shù)的圖象，且為師生對(duì)比因參數(shù)變化導(dǎo)致的函數(shù)圖象變化提供載體，引導(dǎo)學(xué)生在自主探索中獲得新知并對(duì)所學(xué)知識(shí)進(jìn)行遷移運(yùn)用。

【關(guān)鍵詞】信息技術(shù) 高中數(shù)學(xué) 三角函數(shù)圖象

【中圖分類號(hào)】G63 【文獻(xiàn)標(biāo)識(shí)碼】A

【文章編號(hào)】0450-9889（2023）26-0095-04

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017年版2020年修訂）》（以下簡(jiǎn)稱《課程標(biāo)準(zhǔn)》）明確指出，隨著現(xiàn)代科學(xué)技術(shù)特別是計(jì)算機(jī)科學(xué)、人工智能的迅猛發(fā)展，人們獲取數(shù)據(jù)和處理數(shù)據(jù)的能力都得到了很大的提升，伴隨著大數(shù)據(jù)時(shí)代的到來(lái)，人們常常需要對(duì)網(wǎng)絡(luò)、文本、聲音、圖像等反映的信息進(jìn)行數(shù)字化處理，這使數(shù)學(xué)的研究領(lǐng)域與應(yīng)用領(lǐng)域得到極大拓展。在這樣的背景下，數(shù)學(xué)教師有必要挖掘信息技術(shù)與數(shù)學(xué)教學(xué)的契合點(diǎn)，利用信息技術(shù)優(yōu)化教學(xué)資源和教學(xué)設(shè)計(jì)，提高教師的教學(xué)水平和提升學(xué)生的學(xué)習(xí)能力。本文以教學(xué)人教版必修第一冊(cè)第五章第6節(jié)“函數(shù)y=A? sin（ωx+φ）”（第一課時(shí)）為例，闡述在高中數(shù)學(xué)教學(xué)中運(yùn)用信息技術(shù)的實(shí)踐。

一、內(nèi)容分析

課本從用三角函數(shù)刻畫單位圓上以（1，0）為起點(diǎn)、以單位速度逆時(shí)針?lè)较蜻\(yùn)動(dòng)的點(diǎn)出發(fā)，引導(dǎo)學(xué)生思考可以用什么數(shù)學(xué)模型刻畫古代水利灌溉工具——筒車上的點(diǎn)的運(yùn)動(dòng)，讓學(xué)生經(jīng)歷數(shù)學(xué)建模的過(guò)程。通過(guò)類比得出可以利用三角函數(shù)模型y=A? sin（ωx+φ）刻畫筒車的運(yùn)動(dòng)規(guī)律，借助信息技術(shù)，明確研究三角函數(shù)模型y=A? sin（ωx+φ）的思路。

以筒車為研究背景能夠有效地將數(shù)學(xué)學(xué)習(xí)與生活實(shí)際聯(lián)系起來(lái)，對(duì)數(shù)學(xué)建模具有重要的指導(dǎo)意義，同時(shí)以筒車勻速圓周運(yùn)動(dòng)模型來(lái)研究y=A? sin（ωx+φ）中的參數(shù)φ、ω、A對(duì)函數(shù)圖象的影響，符合從特殊到一般的研究方法。

y=A? sin（ωx+φ）中有φ、ω、A三個(gè)參數(shù)，該如何研究？在信息技術(shù)的幫助下，師生可以按照研究問(wèn)題的一般方法，即從簡(jiǎn)單到復(fù)雜、從特殊到一般，循序漸進(jìn)地展開(kāi)，跟隨教材分別探索φ對(duì)y=sin（x+φ）圖象的影響、ω（ω＞0）對(duì)y=sin（ωx+φ）圖象的影響以及A（A＞0）對(duì)y=A? sin（ωx+φ）圖象的影響。

二、學(xué)習(xí)目標(biāo)

結(jié)合筒車運(yùn)動(dòng)的例子，分析勻速圓周運(yùn)動(dòng)涉及的各種量，并利用勻速圓周運(yùn)動(dòng)變化規(guī)律得出這些量之間的相互關(guān)系，進(jìn)而抽象出函數(shù)y=A sin（ωx+φ）并能說(shuō)出參數(shù)φ、ω、A以及變量x、y的物理意義。

會(huì)借助筒車勻速圓周運(yùn)動(dòng)和信息技術(shù)，探索φ對(duì)y=sin（x+φ）圖象的影響、 ω（ω＞0）對(duì)y=sin（ωx+φ）圖象的影響以及A（A＞0）對(duì)y=A? sin（ωx+φ）圖象的影響。

三、教學(xué)評(píng)價(jià)

通過(guò)觀察和借助信息技術(shù)播放筒車的視頻，知道筒車上每一個(gè)盛水筒都做勻速圓周運(yùn)動(dòng)，知道用什么模型來(lái)刻畫筒車的運(yùn)動(dòng)規(guī)律，且了解筒車半徑、筒車轉(zhuǎn)動(dòng)角速度、筒車轉(zhuǎn)動(dòng)時(shí)間三者之間的關(guān)系。

能夠借助筒車勻速圓周運(yùn)動(dòng)和信息技術(shù)，說(shuō)出φ對(duì)y=sin（x+φ）圖象的影響、 ω（ω＞0）對(duì)y=sin（ωx+φ）圖象的影響、 A（A＞0）對(duì)y=A? sin（ωx+φ）圖象的影響。

四、教學(xué)過(guò)程

（一）創(chuàng)設(shè)情境，引出新課

問(wèn)題1：直角坐標(biāo)系中單位圓O上一點(diǎn)，以動(dòng)點(diǎn)A（1，0）為起點(diǎn)按逆時(shí)針?lè)较蛐D(zhuǎn)，旋轉(zhuǎn)角為α，后到達(dá)點(diǎn)P，那么點(diǎn)P的坐標(biāo)（x，y）可以用所學(xué)過(guò)的什么函數(shù)來(lái)確定呢？

學(xué)生根據(jù)前面所學(xué)知識(shí)，易知點(diǎn)P的坐標(biāo)可以用旋轉(zhuǎn)角α的相關(guān)三角函數(shù)x=cosα、y=sinα來(lái)表示。緊接著教師播放微課短視頻，讓學(xué)生觀察動(dòng)點(diǎn)以A（1，0）為起點(diǎn)，以角速度ω=1按逆時(shí)針?lè)较蛐D(zhuǎn)，經(jīng)過(guò)時(shí)間t到達(dá)點(diǎn)P，然后教師提出問(wèn)題：角α與時(shí)間t之間是什么關(guān)系？此時(shí)點(diǎn)P的縱坐標(biāo)y與運(yùn)動(dòng)時(shí)間t之間又可以建立什么樣的關(guān)系呢？那么y是t的函數(shù)關(guān)系嗎？

【設(shè)計(jì)意圖】由已知推廣到未知，讓學(xué)生感受研究一般勻速圓周運(yùn)動(dòng)規(guī)律的必要性，讓學(xué)生明確目標(biāo)，激發(fā)學(xué)習(xí)興趣。

（二）建立模型，提出問(wèn)題

教師播放課前制作的微課短視頻，視頻描繪的是中國(guó)古代發(fā)明的一種灌溉工具——筒車的工作過(guò)程（如圖1所示）。

問(wèn)題2：為方便研究，我們假定在水流相對(duì)穩(wěn)定的條件下，筒車轉(zhuǎn)動(dòng)近似勻速圓周運(yùn)動(dòng)，此時(shí)如果我們把筒車抽象為一個(gè)幾何圖形——圓，將每個(gè)盛水筒看作一個(gè)質(zhì)點(diǎn)，請(qǐng)問(wèn)你能否用一個(gè)數(shù)學(xué)模型來(lái)刻畫盛水筒距離水面的高度與筒車運(yùn)動(dòng)時(shí)間之間的關(guān)系呢？

【設(shè)計(jì)意圖】利用信息技術(shù)展示筒車的運(yùn)動(dòng)場(chǎng)景，讓學(xué)生身臨其境，直觀感受筒車運(yùn)動(dòng)過(guò)程，然后讓學(xué)生觀察、思考，發(fā)表自己的觀點(diǎn)。

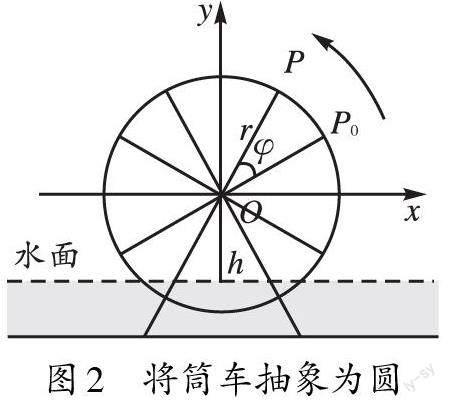
通過(guò)觀看微課視頻，部分學(xué)生能抽象出幾何圖形（如圖2所示）并建立相應(yīng)的直角坐標(biāo)系。在教師的提示下，學(xué)生統(tǒng)一以筒車旋轉(zhuǎn)中心O為原點(diǎn)，水平方向?yàn)閤軸，豎直方向?yàn)閥軸，假定旋轉(zhuǎn)中心O到水面的距離為h，筒車半徑為r，筒車逆時(shí)針旋轉(zhuǎn)角速度為ω，從初始位置P0旋轉(zhuǎn)到終點(diǎn)位置P的時(shí)間為t，OP0為初始邊、OP為終邊的角為φ。

學(xué)生通過(guò)自主探究和合作交流，得出點(diǎn)P的縱坐標(biāo)與上述變量之間的關(guān)系為y=r sin（ωx+φ），記為式子①，同時(shí)得出盛水筒距離水面的高度H與筒車運(yùn)動(dòng)時(shí)間t之間的關(guān)系為H=r sin（ωx+φ）+h，記為式子②。由于h是常量，因此我們要研究盛水筒運(yùn)動(dòng)規(guī)律時(shí)只需研究式子①的性質(zhì)即可，為表述方便，我們研究形如y=A sin（ωx+φ）（A>0，ω>0）的性質(zhì)即可。

【設(shè)計(jì)意圖】從筒車運(yùn)動(dòng)規(guī)律出發(fā)，建立三角函數(shù)模型，獲得研究對(duì)象，培養(yǎng)學(xué)生的數(shù)學(xué)抽象素養(yǎng)。

（三）明確研究y=A sin（ωx+φ）（A>0，ω>0）的思路

問(wèn)題3：式子y=A sin（ωx+φ）（A>0，ω>0）中的參數(shù)較多，有A、ω、φ三個(gè)，我們?nèi)绾伍_(kāi)展研究呢？

學(xué)生已經(jīng)學(xué)過(guò)正弦函數(shù)y=sinx的圖象和性質(zhì)，而當(dāng)取A=1、ω=1、φ=0時(shí)y=A sin（ωx+φ）（A>0，ω>0）就變成了正弦函數(shù)y=sinx，因此可以從正弦函數(shù)y=sinx開(kāi)始研究。接下來(lái)先研究三個(gè)參數(shù)A、ω、φ中的哪一個(gè)并沒(méi)有什么特別的規(guī)定。教師結(jié)合學(xué)生熟知平移變換這一情況，引導(dǎo)學(xué)生先研究φ對(duì)函數(shù)y=A sin（ωx+φ）（A>0，ω>0）圖象的影響，再研究ω對(duì)函數(shù)y=A sin（ωx+φ）（A>0，ω>0）圖象的影響，最后研究A對(duì)函數(shù)y=A sin（ωx+φ）（A>0，ω>0）圖象的影響，這樣既符合知識(shí)的遷移規(guī)律，又符合學(xué)生的認(rèn)知規(guī)律。

【設(shè)計(jì)意圖】讓學(xué)生掌握研究問(wèn)題的基本思路：從簡(jiǎn)單到復(fù)雜、從特殊到一般。前面得出可以用y=A sin（ωx+φ）（A>0，ω>0）刻畫筒車運(yùn)動(dòng)模型，為更好地了解筒車運(yùn)動(dòng)的規(guī)律，需要研究函數(shù)y=A sin（ωx+φ）（A>0，ω>0）的性質(zhì)。對(duì)A、ω、φ賦值我們發(fā)現(xiàn)，當(dāng)A=1、ω=1、φ=0時(shí)，復(fù)雜的三角函數(shù)y=A sin（ωx+φ）（A>0，ω>0）就變成了正弦函數(shù)y=sinx，學(xué)生是熟悉正弦函數(shù)的性質(zhì)的，在此基礎(chǔ)上依次深入研究不同參數(shù)，符合學(xué)生的認(rèn)知發(fā)展規(guī)律，也符合研究問(wèn)題的基本思路。

（四）探索φ對(duì)y=sin（x+φ）圖象的影響

為讓學(xué)生直觀感受φ對(duì)y=sin（x+φ）圖象的影響，筆者提前借助信息技術(shù)制作微課，用動(dòng)畫展示盛水筒運(yùn)動(dòng)軌跡，當(dāng)取A=1、ω=1時(shí)，動(dòng)點(diǎn)M在以O(shè)1為圓心的單位圓上以單位角速度逆時(shí)針旋轉(zhuǎn)。當(dāng)取φ=0時(shí)，此時(shí)動(dòng)點(diǎn)M從點(diǎn)Q0逆時(shí)針勻速出發(fā)，時(shí)間x為橫坐標(biāo)，高度為縱坐標(biāo)，把相應(yīng)的點(diǎn)（x，y）描出來(lái)，就得到虛線所示曲線，當(dāng)動(dòng)點(diǎn)一直在圓周上逆時(shí)針旋轉(zhuǎn)時(shí)，虛線曲線也會(huì)一直往x軸正方向重復(fù)出現(xiàn)；當(dāng)取[φ=π6]時(shí)，此時(shí)動(dòng)點(diǎn)M從點(diǎn)Q1逆時(shí)針勻速出發(fā)，重復(fù)上面的操作就會(huì)得到如圖3所示的實(shí)線曲線。

為讓學(xué)生獲得更直觀的感受，教師邀請(qǐng)幾名學(xué)生到講臺(tái)上，借助信息技術(shù)感受分別當(dāng)[φ=-π/6]、[φ=π/3]、[φ=-π/3]時(shí)，動(dòng)點(diǎn)按逆時(shí)針?lè)较蛐D(zhuǎn)所對(duì)應(yīng)點(diǎn)（x，y）的軌跡。

學(xué)生觀察和操作后得出結(jié)論：函數(shù)y=sin（x+φ）的圖象是由y=sinx向左（φ>0）或向右（φ<0）平移|φ|個(gè)單位得到的。

數(shù)學(xué)來(lái)源于生活又應(yīng)用于生活，此時(shí)教師在課堂上繼續(xù)追問(wèn)：這些不同的φ值相當(dāng)于筒車當(dāng)中的什么呢？通過(guò)思考，大部分學(xué)生都能回答出：這些不同的φ值相當(dāng)于筒車中盛水筒的初始位置所對(duì)應(yīng)的角度大小。

【設(shè)計(jì)意圖】讓學(xué)生借助信息技術(shù)感受當(dāng)φ取不同值時(shí)函數(shù)y=sin（x+φ）圖象的變化，得出φ對(duì)函數(shù)y=sin（x+φ）圖象影響的一般規(guī)律：函數(shù)y=sin（x+φ）的圖象是由y=sinx向左（φ>0）或向右（φ<0）平移|φ|個(gè)單位得到的，發(fā)展學(xué)生的觀察能力與總結(jié)歸納能力。

（五）探索ω（ω>0）對(duì)y=sin（x+φ）圖象的影響

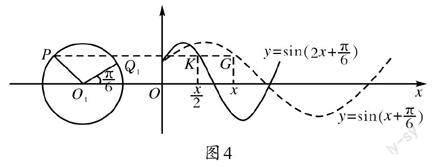
同前面探索φ對(duì)y=sin（x+φ）圖象的影響的過(guò)程一樣，教師先借助多媒體進(jìn)行演示。當(dāng)ω=1時(shí)，對(duì)函數(shù)y=sin（x+[π/6]）而言，動(dòng)點(diǎn)M從Q位置出發(fā)，經(jīng)過(guò)x s到達(dá)點(diǎn)P，則點(diǎn)G（x，y）在y=sin（x+[π/6]）的圖象上；而當(dāng)ω=2時(shí)，對(duì)函數(shù)y=sin（2x+[π/6]）而言，動(dòng)點(diǎn)M從Q1位置出發(fā)，只需要經(jīng)過(guò)[x2] s即可到達(dá)點(diǎn)P，因此點(diǎn)K（[x2]，y）在y=sin（2x+[π/6]）的圖象上（如圖4所示）。學(xué)生觀察后可以得出如下結(jié)論：只需要把y=sin（x+[π/6]）的圖象壓縮為原來(lái)的[12]即可得到y(tǒng)=sin（2x+[π6]）的圖象。

隨后，教師讓學(xué)生借助信息技術(shù)操作并思考，當(dāng)ω=[1/2]、ω=3、ω=[1/3]時(shí)，y=sin（[1/2]x+[π/6]）、y=sin（[3]x+[π/6]）、y=sin（[1/3]x+[π/6]）的圖象和y=sin（x+[π/6]）的圖象相比較有哪些變化。

通過(guò)觀察與討論，學(xué)生歸納出下列一般性的結(jié)論：函數(shù)y=sin（[ω]x+φ）的圖象是由y=sin（x+φ）的橫坐標(biāo)伸長(zhǎng)（[ω]<1）或縮短（[ω]>1）為原來(lái)的[1ω]個(gè)單位、縱坐標(biāo)不變得到的。

在筒車運(yùn)動(dòng)的實(shí)驗(yàn)中，[ω]體現(xiàn)的是筒車上盛水筒逆時(shí)針旋轉(zhuǎn)的速度。借助信息技術(shù)得出結(jié)論之后仍需要用結(jié)論來(lái)檢驗(yàn)生活中的事實(shí)是否符合研究結(jié)果。

【設(shè)計(jì)意圖】教師首先利用信息技術(shù)出示函數(shù)y=sin（x+[π/6]）和y=sin（2x+[π/6]）的圖象，引導(dǎo)學(xué)生比較并歸納得出結(jié)論，然后讓學(xué)生自己用信息技術(shù)分別作出當(dāng)ω=[1/2]、ω=3、ω=[1/3]時(shí)的函數(shù)圖象并對(duì)以上所有圖象進(jìn)行比較，總結(jié)得出ω對(duì)y=sin（[ω]x+[π/6]）圖象影響的一般結(jié)論，發(fā)展學(xué)生的觀察能力、動(dòng)手能力以及總結(jié)歸納能力。

（六）探索A（A>0）對(duì)y=A sin（[ω]x+φ）圖象的影響

師生已經(jīng)探索了φ對(duì)y=sin（x+φ）和[ω]（[ω]>0）對(duì)y=sin（[ω]x+φ）圖象的影響，都是借助信息技術(shù)手段和運(yùn)用從特殊到一般的研究方法歸納得出結(jié)論的。接下來(lái)可以利用同樣的方法，探索A（A>0）對(duì)y=A sin（[ω]x+φ）圖象的影響。

教師先借助信息技術(shù)在坐標(biāo)系中畫出函數(shù)y=sin（2x+[π/6]）的圖象，在這個(gè)圖象中單位圓O1上的點(diǎn)Q1以[ω]=2的角速度逆時(shí)針旋轉(zhuǎn)x s到點(diǎn)P，則坐標(biāo)K（x，sin（2x+[π/6]））在函數(shù)y=sin（2x+[π/6]）圖象上。此時(shí)以O(shè)1為圓心，作一個(gè)半徑為2的圓，射線O1Q1與此圓相交于點(diǎn)T1，T1在該圓上以[ω]=2的角速度逆時(shí)針旋轉(zhuǎn)x s到點(diǎn)T，則坐標(biāo)N（x，2sin（2x+[π/6]））在函數(shù)y=2sin（2x+[π/6]）圖象上（如圖5所示）。此時(shí)，教師繼續(xù)利用信息技術(shù)在直角坐標(biāo)系中畫出函數(shù)y=[12]sin（2x+[π/6]）、y=3sin（2x+[π/6]）、y=[13]sin（2x+[π/6]）的圖象。

學(xué)生通過(guò)觀察、類比、歸納等方法，得出如下一般性結(jié)論：函數(shù)y=A sin（[ω]x+φ）的圖象是由y=sin（[ω]x+φ）縱坐標(biāo)伸長(zhǎng)（A>1）或縮短（A<1）為原來(lái)的A倍、橫坐標(biāo)不變得到的。

【設(shè)計(jì)意圖】學(xué)生經(jīng)歷了探索φ對(duì)y=sin（x+φ）圖象的影響和探索ω（ω>0）對(duì)y=sin（ωx+φ）圖象的影響的過(guò)程，探索A（A>0）對(duì)y=Asin（ωx+φ）圖象的影響對(duì)此時(shí)的他們而言比較簡(jiǎn)單，因此教師利用信息技術(shù)軟件演示y=sin（2x+[π/6]）、y=[12]sin（2x+[π/6]）、y=3sin（2x+[π/6]）、y=[1/3]sin（2x+[π/6]）的圖象，讓學(xué)生觀察、歸納總結(jié)即可得出一般性結(jié)論。

五、教學(xué)反思

數(shù)學(xué)抽象是數(shù)學(xué)學(xué)科核心素養(yǎng)之一，高中數(shù)學(xué)知識(shí)大多比較抽象，高中生尤其是高一年級(jí)學(xué)生的抽象能力有限，在不借助任何工具的情況下，相當(dāng)一部分學(xué)生難以學(xué)好高中數(shù)學(xué)。為了讓學(xué)生更加深入地學(xué)習(xí)函數(shù)y=Asin（ωx+φ）的相關(guān)知識(shí)，教師運(yùn)用信息技術(shù)手段，促進(jìn)學(xué)生思考，發(fā)展了學(xué)生的數(shù)學(xué)學(xué)科核心素養(yǎng)。本節(jié)課，將信息技術(shù)融入數(shù)學(xué)課堂教學(xué)的優(yōu)勢(shì)主要體現(xiàn)在以下兩個(gè)方面。

（一）重視數(shù)學(xué)情境，激發(fā)學(xué)習(xí)興趣

教育必須與生產(chǎn)勞動(dòng)和社會(huì)實(shí)踐相結(jié)合，培養(yǎng)德智體美勞全面發(fā)展的社會(huì)主義建設(shè)者和接班人。數(shù)學(xué)學(xué)習(xí)不能只重視知識(shí)和技能的學(xué)習(xí)，數(shù)學(xué)教師也不應(yīng)該只做“教書匠”。本節(jié)課教師通過(guò)制作短視頻，以古代發(fā)明的水利灌溉工具——筒車為背景引入課題，引入環(huán)節(jié)生動(dòng)形象，貼近社會(huì)生產(chǎn)勞動(dòng)實(shí)際，說(shuō)明數(shù)學(xué)來(lái)源于生活的同時(shí)又應(yīng)用于生活，教師在課堂上結(jié)合情境提出恰當(dāng)問(wèn)題，學(xué)生根據(jù)情境找到解決問(wèn)題的方法，幫助學(xué)生更深入地認(rèn)識(shí)和理解數(shù)學(xué)，激發(fā)了學(xué)生學(xué)習(xí)數(shù)學(xué)和探究數(shù)學(xué)的興趣。

（二）重視數(shù)學(xué)思維，發(fā)展核心素養(yǎng)

教學(xué)中研究參數(shù)A、ω、φ對(duì)函數(shù)y=Asin（ωx+φ）（A>0，ω>0）圖象的影響時(shí)，教師先引導(dǎo)學(xué)生根據(jù)筒車運(yùn)動(dòng)情境探討參數(shù)研究順序，雖然學(xué)生提出了不同的研究順序，但在信息技術(shù)的輔助以及教師的點(diǎn)撥下，學(xué)生最后得出一致的研究思路：先研究參數(shù)φ對(duì)函數(shù)y=sin（x+φ）圖象的影響、再研究參數(shù)ω（ω>0）對(duì)函數(shù)y=sin（ωx+φ）（ω>0）圖象的影響、最后研究參數(shù)A（A>0）對(duì)函數(shù)y=A sin（ωx+φ）（A>0，ω>0）圖象的影響，這樣符合從已知到未知、從簡(jiǎn)單到復(fù)雜、從特殊到一般的研究方法，最后抽象歸納出筒車運(yùn)動(dòng)規(guī)律模型的研究思路，豐富學(xué)習(xí)經(jīng)驗(yàn)，發(fā)展核心素養(yǎng)。

總之，信息技術(shù)融入高中數(shù)學(xué)課堂教學(xué)已是必然，新時(shí)代教師除了提高專業(yè)技術(shù)水平，還要學(xué)習(xí)信息技術(shù)等知識(shí)來(lái)輔助教學(xué)，不斷優(yōu)化教學(xué)，使教育真正為社會(huì)主義現(xiàn)代化建設(shè)服務(wù)、為人民服務(wù)，落實(shí)立德樹人根本任務(wù)。

參考文獻(xiàn)

［1］章建躍.核心素養(yǎng)立意的高中數(shù)學(xué)課程教材教法研究［M］.上海：華東師范大學(xué)出版社，2021.

作者簡(jiǎn)介：左國(guó)云（1981— ），廣西凌云人，本科，學(xué)士，高級(jí)教師，主要從事高中數(shù)學(xué)教學(xué)研究。

（責(zé)編 劉小瑗）