基于流場特性分析的安全殼整體性密封性試驗方法研究

婁淑雅 ，顧濟民，沈東明，何 銳，黃曉明,*，許國良

（1.華中科技大學(xué)能源與動力工程學(xué)院，湖北 武漢 430074；2.中廣核工程有限公司核電安全監(jiān)控技術(shù)與裝備國家重點實驗室，廣東 深圳 518172）

作為核電站縱深防御原則的最后一道實體屏障，確保安全殼在任何情況下的密封性對核安全有著重要的意義[1]。整體泄漏率試驗（Integrated Leakage Rate Test，ILRT）是目前監(jiān)督安全殼整體密封性是否滿足要求的重要手段[2-5]。整體泄漏率無法直接測量，因此整體密封性試驗的原理是在設(shè)計壓力下，通過連續(xù)測量安全殼內(nèi)壓力、溫度和相對濕度，再依據(jù)理想氣體狀態(tài)方程計算出安全殼內(nèi)空氣總質(zhì)量變化規(guī)律，以確定整體泄漏率[6-8]。這種氣體流量計量方法又被稱為pVTt 法[9]。可以看出，安全殼泄漏率測量的準確性十分依賴整體密封試驗過程中測點布置和平均參數(shù)的計量方法[10,11]。

核電站安全殼內(nèi)部凈容積相當大，如CPR1000 安全殼內(nèi)部自由空間約49 400 m3，EPR 安全殼內(nèi)部自由空間約為78 000 m3。此外，安全殼內(nèi)部空間因設(shè)備安裝和工藝要求被分隔成若干個隔間，這些隔間布置對安全殼內(nèi)氣體的流動與傳輸有著很大的影響。因此，安全殼內(nèi)部的溫度分布和濕度分布是不均勻的，需要布置許多有代表性的傳感器進行測量。通常，幾萬方的自由空間只能設(shè)置70～100 個溫度傳感器，每個傳感器的測得值分配了一定的自由容積值Vi，Vi與安全殼總自由空間V的比值被稱為該傳感器的權(quán)重因子。將傳感器的測量值根據(jù)權(quán)重因子進行加權(quán)平均，計算出平均溫度，是安全殼整體泄漏率計算中的重要步驟[12-14]。

文獻[15-17]指出，安全殼內(nèi)的溫度場不均勻性使得傳感器布置和體積分配系數(shù)的確定具有很大不確定性，因此，掌握安全殼內(nèi)流場和溫度場分布情況是合理布置測溫點的前提。然而，安全殼體積龐大，空間布置復(fù)雜，充氣過程和穩(wěn)壓過程均具有強烈的非穩(wěn)態(tài)特性，試驗和分析方法在研究其流動與傳熱特性方面十分受限。而采用計算流體力學(xué)（CFD）仿真技術(shù)，不僅成本低、耗時少，還能模擬各種復(fù)雜或理想的試驗過程[8]，十分有助于指導(dǎo)安全殼整體密封性試驗方法的改進和優(yōu)化。但對安全殼整體密封性試驗過程進行CFD 仿真模擬研究的相對較少[15,18]，至今未見有研究者對全尺寸安全殼整體密封性試驗的充氣和穩(wěn)壓過程進行數(shù)值研究。

本文建立了一個安全殼及其內(nèi)部構(gòu)筑物的CFD 仿真模型，基于ANSYS Fluent 商用流體仿真軟件，對安全殼打壓（充氣）試驗和保壓試驗進行模擬，分析了其內(nèi)部氣體流動規(guī)律和溫度分布規(guī)律。同時，本文還基于數(shù)值模擬結(jié)果，對不同測點布置方案得到的干空氣質(zhì)量準確性的定量研究，初步探索了提高整體試驗精度的途徑和方法。

1 數(shù)學(xué)物理模型

1.1 幾何模型

采用簡化的某安全殼模型作為研究對象，安全殼高度約為 60 m，內(nèi)徑為40 m。建模過程是按照標高分塊，將模型分為四個主要空間：一層（標高0.00～4.00 m）、二層（4.00～7.35 m）、三層（7.35～38.00 m）及安全殼筒體（-0.50～59.88 m）。如圖1 所示，安全殼空間內(nèi)主要設(shè)備包含2 臺蒸汽發(fā)生器、2 臺冷卻劑泵、1 臺穩(wěn)壓器，構(gòu)筑物隔間布置則考慮了堆坑、再生熱交換器、閥門間、通風(fēng)冷卻口隔間、卸壓箱隔間、通風(fēng)機隔間、堆內(nèi)構(gòu)件存放池、安注箱隔間、余熱排出泵隔間等。各樓層之間保留了必要的通道，確保空氣流通與實際安全殼的相似性。安全殼與主要樓層隔間之間還有一個繞堆坑外墻的公用環(huán)廊區(qū)，位于層高4.63 m 處，它與蒸汽發(fā)生器隔間、主泵隔間大面積相連通。安全殼內(nèi)部總體積為72 322 m3，其中，氣體空間體積為63 606 m3。

圖1 某安全殼簡化三維幾何模型Fig.1 The 3D geometric model of a simplified containment vessel

1.2 數(shù)學(xué)模型

視空氣為可壓縮氣體，建立其三維流動與傳熱數(shù)學(xué)模型。主要控制方程包括連續(xù)性方程、動量方程、能量方程和湍流流動控制方程。具體如下：

連續(xù)性方程：

其中：ρ——密度；

u——速度。

動量方程：

其中：τ——黏度壓力張量，Pa。

能量方程：

其中：cp——定壓比熱容；

T——溫度；

λ——流體的傳熱系數(shù)；

Sr——流體的內(nèi)熱源及由于黏性耗散項。

湍流模型采用標準k-ε模型。標準k-ε模型需要求解湍動能及其耗散率方程，具體形式如下：

其中，μ——流體黏性系數(shù)；

μt——湍流黏性系數(shù)；

σk、σε——湍流普朗特數(shù)；

Gk——平均速度梯度所導(dǎo)致的湍流動能產(chǎn)生項；

Gb——浮力所導(dǎo)致的湍流動能產(chǎn)生項；

YM——可壓縮湍流中擴張導(dǎo)致的波動對湍流耗散率的整體影響；

C1ε、C2ε、C3ε——湍流輸運方程常數(shù)。湍流黏性系數(shù)通過k和ε計算得到：

本文取C1ε=1.44，C1ε=1.92，Cμ=0.09，湍動能k與耗散率ε的湍流普朗特數(shù)分別為σk=1.0、σε=1.3。浮力對湍流耗散率的影響程度由常數(shù)C3ε決定：

其中：vpa——平行于重力方向的速度分量；

vper——垂直于重力方向的速度分量。

Gk在標準k-ε模型和RNGk-ε模型中都是一樣的表達，由湍流動能k的輸運方程可以推出：

k-ε模型在k和ε方程中均考慮了浮力的影響，浮力由下式給出：

其中：Prt——湍流能量普朗特數(shù)，對于標準k-ε模型，Prt的默認值是0.85；

gi——重力在i方向上的分量；熱膨脹系數(shù)β定義為：

YM通過下式計算：

其中：Mt——湍流Mach 數(shù)。

1.3 邊界條件和基本假設(shè)

安全殼內(nèi)初始空氣的溫度為300 K，壓力為大氣壓力。整個計算過程包括80 min 充氣過程，40 min 穩(wěn)壓過程。該過程模擬了實際打壓過程第一個微小壓力上升平臺。充氣過程的進氣量為7 000 Nm3/h，進風(fēng)口設(shè)置在層高y=4.2 m 處（z=0 截面經(jīng)過其中心截面），定義為水平速度入口邊界，送風(fēng)速度和溫度分別為：2.289 kg/s和300 K。進入穩(wěn)壓過程后，入口關(guān)閉。在充氣和穩(wěn)壓的過程中，均不考慮任何氣體出口，安全殼被假想為密閉的壓力容器。考慮浮力模型，重力加速度為9.8 m/s2。

在傳熱方面，僅考慮充入的壓縮空氣與安全殼內(nèi)空氣之間的混合換熱，不考慮氣體與內(nèi)部設(shè)備、隔間壁面的對流換熱，即壁面取絕熱。安全殼的周壁盡管會受到環(huán)境條件的影響，如風(fēng)、雨、陽光等造成的外部散熱或外部加熱環(huán)境，但考慮安全殼壁面厚度大于1 m，這些換熱對殼內(nèi)空氣的影響微乎其微，因此安全殼周壁也設(shè)置為絕熱。

2 網(wǎng)格獨立性驗證與熱力學(xué)驗證

安全殼內(nèi)部計算域采用非結(jié)構(gòu)網(wǎng)格，本文采用了 ANSYS Meshing 中的四面體網(wǎng)格（Tetrahedrons）及Patch Conforming 算法網(wǎng)格劃分方法，倒角處網(wǎng)格進行細化。第一、二、三層隔間區(qū)設(shè)備隔間布置較為復(fù)雜，因此對這些區(qū)域的網(wǎng)格均進行了適當加密。最終得到網(wǎng)格數(shù)量為43 萬（模型2），默認網(wǎng)格大小為2.0 m，選擇捕捉曲率，曲率最小尺寸為0.1 m，曲率法向角為15°；選擇捕捉鄰近性，鄰近性最小尺寸為1.0 m，跨間隙單元格數(shù)為4。為了考察網(wǎng)格數(shù)量和密度對計算結(jié)果的影響，本文還采用3 萬（模型1）和266 萬（模型3）的網(wǎng)格進行相同工況的模擬，入口位置的基礎(chǔ)均為0.05 m。

通過比較七個監(jiān)測點（見圖1）的溫度和速度計算值來檢驗網(wǎng)格獨立性。計算結(jié)果表明，其中六個點對網(wǎng)格密度不敏感，但位于入口上方的e1 點對網(wǎng)格劃分方法有一定敏感性。三種網(wǎng)格劃分方法下得到的e1 的溫度隨時間變化規(guī)律如圖2（a）所示，顯然粗網(wǎng)格（模型1）的結(jié)果與其他兩種細網(wǎng)格相比，有一定偏差。為了節(jié)約計算成本與時間本文選取模型2 的網(wǎng)格劃分方法。

圖2 網(wǎng)格獨立性驗證及熱力學(xué)驗證Fig.2 Verification of grid independence and thermodynamics

為進一步驗證網(wǎng)格的合適性，我們將數(shù)值計算結(jié)果與熱力學(xué)分析結(jié)果進行對比。根據(jù)熱力學(xué)第一定律，安全殼在打壓充氣期間能量方程滿足式（12）[19]：

其中：m1——打壓前安全殼內(nèi)空氣的質(zhì)量；

m2——任意時刻安全殼內(nèi)空氣質(zhì)量；

u——比熱力學(xué)能；

hin——進口空氣的比焓；

min——充氣過程期間充入安全殼內(nèi)的質(zhì)量，其值為進風(fēng)口質(zhì)量流量與充氣時間的乘積。

cvi和cpi——該時刻空氣的比定容熱容與比定壓熱容。

通過式（12）～式（15）聯(lián)立可以得到不同時刻安全殼內(nèi)平均溫度與平均壓力的理論值，將其與模型2、模型3 對應(yīng)時刻的平均溫度與平均壓力進行對比，如圖2（b）所示。由圖可看出模型2 和模型3 的平均溫度和平均壓力相當，都與熱力學(xué)計算的理論值吻合得較好。

3 安全殼內(nèi)流動與傳熱特性分析

3.1 速度場

圖3 給出了充氣40 min、充氣80 min 以及穩(wěn)壓40 min 時，安全殼內(nèi)x=0 截面的速度場和流線分布。由圖3（a）可以看出，受進氣流影響環(huán)廊區(qū)域流動最為強烈，其次是一、二層底部空間和頂部自由空間；三層隔間連通性較差，各個隔間內(nèi)氣體流動均較弱。由圖3（b）可以看出，當充氣過程進行到80 min 時，氣體流動增強的區(qū)域增多，但明顯氣流受到的阻力也增大；環(huán)廊仍保持了較強烈的流動，頂部大空間和一、二層隔間處則有明顯的渦流。由圖3（c）可以看出，穩(wěn)壓40 min 后安全殼內(nèi)氣體的流動已整體較弱，主要依靠氣體浮升力的驅(qū)動，其流動方向與充氣過程相反。相比頂部自由空間和環(huán)廊，一、二、三層隔間內(nèi)的氣體流動都較弱。根據(jù)流體特性來看，安全殼大致可分為四個不同區(qū)域：環(huán)廊區(qū)域、包含一層和二層的底部隔間區(qū)域、三層隔間區(qū)域以及頂部大空間區(qū)域。

圖3 安全殼內(nèi)氣體速度分布和流場特征（x=0）Fig.3 Characteristics of the gas velocity distribution and the flow field in the containment (x=0)

3.2 溫度場

圖4 給出了三個時刻，即充氣40 min、充氣80 min 以及穩(wěn)壓40 min，安全殼內(nèi)空氣的溫度場分布。圖4（a）因為還在打壓過程的中期，溫度整體比后兩個時刻低很多，安全殼內(nèi)氣體的最高溫度為309 K。由圖4（b）可以看出，充氣80 min 時，安全殼氣體溫度都上升了，最高溫度達到318 K。顯然，這些熱量的來源是充入氣體帶進來的焓值。同時可以看到，溫度較高的區(qū)域?qū)?yīng)了流動較弱的區(qū)域，即壓縮效應(yīng)更為明顯的區(qū)域。圖4（c）顯示，穩(wěn)壓過程進行到足夠深時，安全殼內(nèi)大部分區(qū)域的溫度都較為均勻，但幾個分區(qū)的溫度還是會有一定差異。三層隔間內(nèi)溫度最高，環(huán)廊區(qū)域溫度最低，底部隔間區(qū)域略低于三層隔間內(nèi)，頂部大空間則有分層現(xiàn)象。

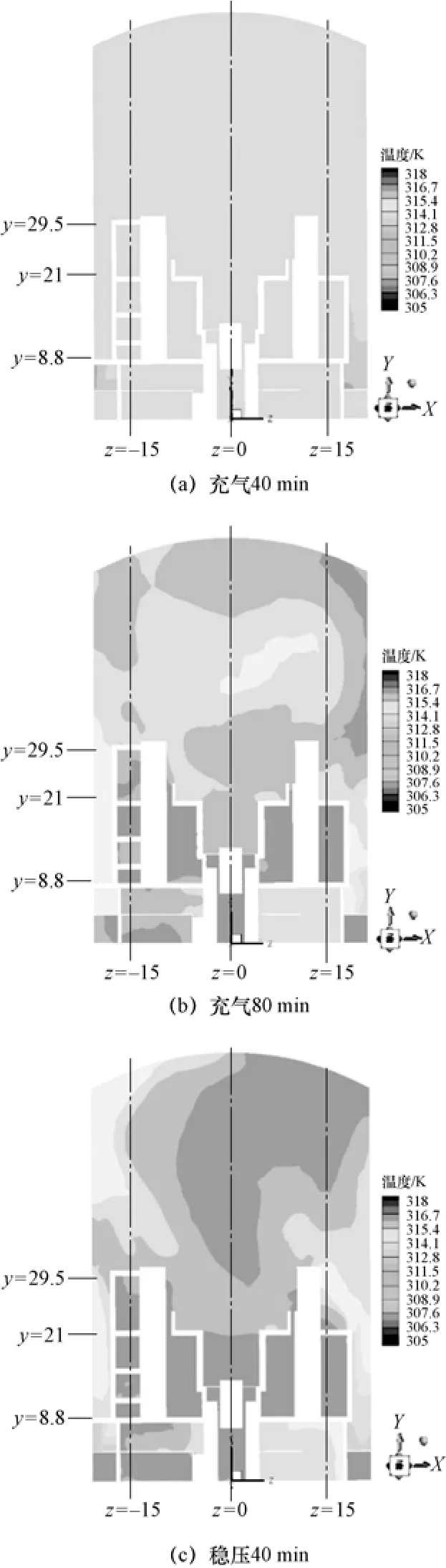
圖4 安全殼內(nèi)氣體的溫度分布（x=0）Fig.4 The temperature distribution of gas in the containment (x=0)

在x=0 截面上取z=-15 m、z=0 m、z=15 m 處，觀察三個時刻空氣沿高度方向的溫度分布，如圖5 所示。可以看到，在充氣過程的早期階段，如圖5（a）所示，安全殼內(nèi)大部分區(qū)域溫度都較為均勻，即使有局部點溫度較低，最大溫差不超過0.7 ℃。當充氣過程進行到80 min 后，如圖5（b）所示，無論是高度方向，還是水平方向，都出現(xiàn)了較大的溫度不均勻性，流動越弱的區(qū)域溫度越高，多個截面的局部溫差達到2.5 ℃左右。穩(wěn)壓40 min 時，如圖5（c）所示，盡管流動已經(jīng)較弱，但安全殼內(nèi)各區(qū)域的溫度仍不均勻。差異較大的區(qū)域主要體現(xiàn)在底部隔間和頂部，局部溫差約2.0 ℃。

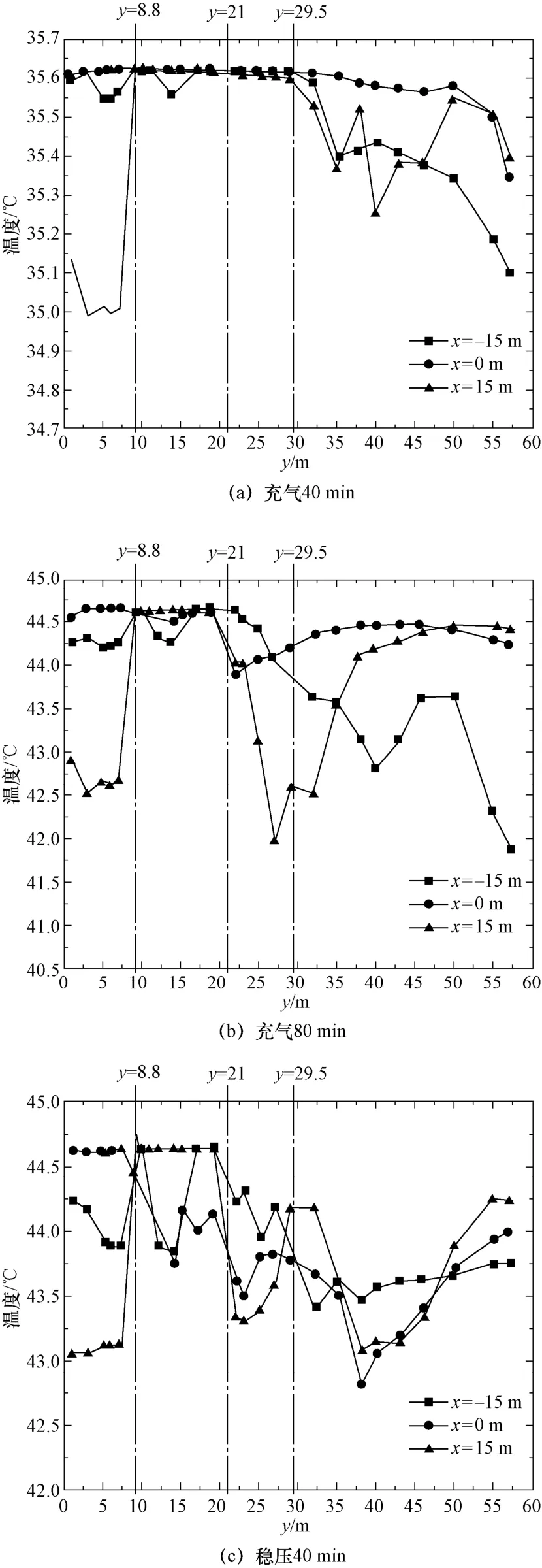
圖5 安全殼內(nèi)溫度沿高度y 方向的分布Fig.5 The temperature distribution in the containment along y direction

4 測點布置對干空氣質(zhì)量計算的影響

4.1 安全殼內(nèi)干空氣質(zhì)量的計算方法

安全殼的泄漏率不能直接測量，需要根據(jù)殼內(nèi)空氣質(zhì)量變化間接計算。基于多點測量方法獲得安全殼平均溫度、平均壓力，利用理想氣體狀態(tài)方程（16）即可獲得某時刻空氣質(zhì)量：

式中：Pa——氣體壓力；

V——安全殼總自由容積；

m——任意時刻殼內(nèi)干空氣的總質(zhì)量；

Rg——干空氣的氣體常數(shù)；

式中：Vi——第i個溫度儀表所代表的周圍自由空間氣體體積；

Ti——第i個溫度儀表的測量數(shù)據(jù)。

可以看出，各個儀表所代表的容積Vi的準確性直接影響到計算結(jié)果的準確性。

4.2 兩種測量方案及比較

本文將基于上面的仿真結(jié)果對兩種傳感器布置方案的優(yōu)劣進行對比，探討安全殼內(nèi)傳感器布置對安全殼質(zhì)量測量準確性的影響。測點當?shù)氐臏囟扔嬎阒当蛔鳛闇y量值，每個測點分配一定儀表代表容積。值得注意的是，本文的目的是探討傳感器布置的原則，因此，所提出的兩種方案是結(jié)合仿真結(jié)果流場和溫度場而定的較為理想的情況，并沒有參考現(xiàn)有電站A 類試驗的實際布點方案。

方案一考慮一種較為稀疏的布置方案，僅依據(jù)流場將安全殼粗略劃分為7 個自由空間，每個空間設(shè)置一個溫度測點，測點在安全殼的位置如圖1 所示。方案二則基于溫度場對這7個自由空間進行了進一步細分，設(shè)置了22 個測點。表1 以方案一為例給出了測點位置、代表空間、分配容積和容積加權(quán)因子的具體信息，圖6 則進一步以面積占比表征容積占比的形式，繪制出了兩種方案中各測點所代表的空間的相對位置、相對比例和彼此聯(lián)通的情況。

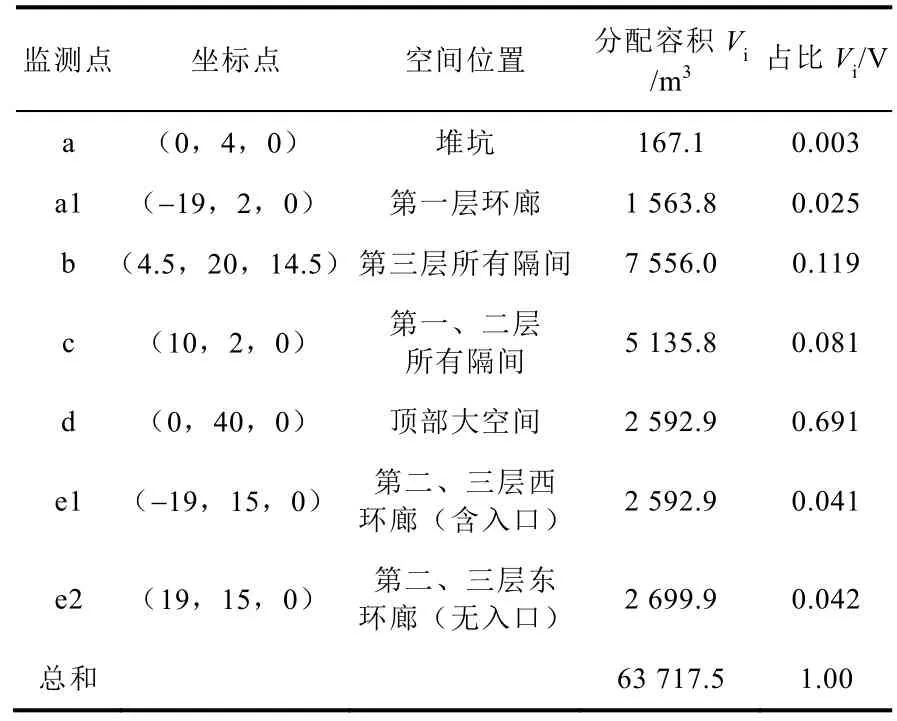
表1 七個測量點在安全殼內(nèi)的位置及體積權(quán)重因子Table 1 Positions and volume weights of seven measuring points in the containment vessel

采用測量值與理論值比較的方式來評價測量值的準確性。理論值mth為通過入口進入安全殼的進氣總量min和初始質(zhì)量m0的總和。測量值為根據(jù)式（16）和式（17）計算得到的空氣質(zhì)量msim。測量誤差ε定義如下：

圖7 給出了不同時刻兩種方案測量值的誤差比較。可以看出，兩種方案的測量誤差都與時間有關(guān)，即受到安全殼內(nèi)流動與傳熱過程的影響。充壓階段的測量誤差隨著時間先增長再降低，穩(wěn)壓階段測量誤差逐漸降低。大多數(shù)時刻，方案二的誤差都小于方案一，但在穩(wěn)壓過程進行一段時間后，方案一的測量誤差急劇減小，似乎更為精確。但事實上，本文計算過程中穩(wěn)壓階段的空氣質(zhì)量理論值為常數(shù)，因此方案一的測量值并沒有反映質(zhì)量隨時間變化的真實情況，而方案二則較好地反映了穩(wěn)壓過程的這一規(guī)律。綜合各個時刻的情況，方案二的測量結(jié)果更為可靠。

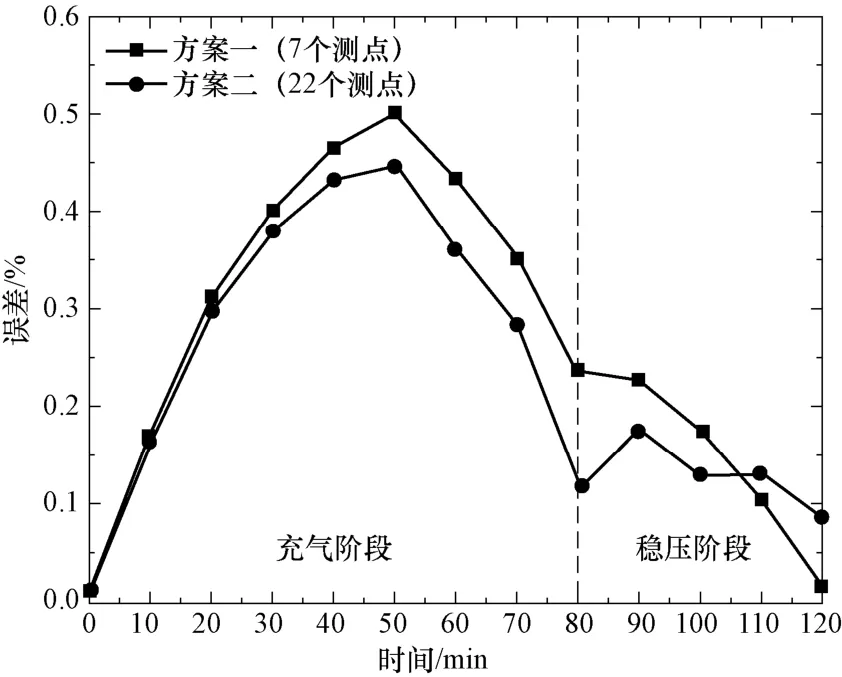
圖7 兩種方案的測量值誤差Fig.7 Measurement errors of the two schemes

4.3 不良測點修正的討論

目前，對在役安全殼密封性的長期監(jiān)控也是核工業(yè)界較為關(guān)注的技術(shù)研究方向。由于核電站的特殊性，儀表維護只能定期進行。因此，在役測量需要考慮局部儀表故障時的數(shù)據(jù)處理方法，一般會采用與相鄰儀表代表容積合并的方法[2]。本文嘗試基于仿真數(shù)據(jù)結(jié)果對合并容積的選擇合理性進行探討。

以上面給出的22 個測點的方案二為例，假設(shè)測點a1 發(fā)生儀表故障，分別選取了四種相鄰儀表合并方案。其中，方案A 考慮相鄰且聯(lián)通原則將a1 和c 的代表容積相合并，方案B 考慮相鄰且流場相似原則將a1 和a 的代表容積相合并。方案C 和方案D 都僅考慮了相鄰原則，將a1 分別和e1、e4 的代表容積合并。e1 和e4 與a1 的連通性均較弱，流動和傳熱特性也差異較大。其中，e1 與e4 的區(qū)別是e1 中包含了空氣入口。各種方案重新計算得到的干空氣質(zhì)量msim_i與原方案msim_22之間的偏差用 'ε表示：

圖8 給出了不同時刻四種方案的測量偏差值。可以看到考慮相鄰且流場相似原則的方案B 引起的測量偏差最小。考慮了相鄰且連通的方案A 偏差略高，但在穩(wěn)壓區(qū)偏差非常穩(wěn)定，因此得到的質(zhì)量變化率仍是可靠性較高的。方案C 和方案D 因為合并時未考慮流場和溫度場的差異，引起了較大偏差。其中方案C 因為受到入口流動的影響，在充氣段引起的誤差尤其大，在穩(wěn)壓段逐漸減小并趨于穩(wěn)定。而方案D雖然在充氣段小于方案C，但在穩(wěn)壓段偏差卻較大且有波動。

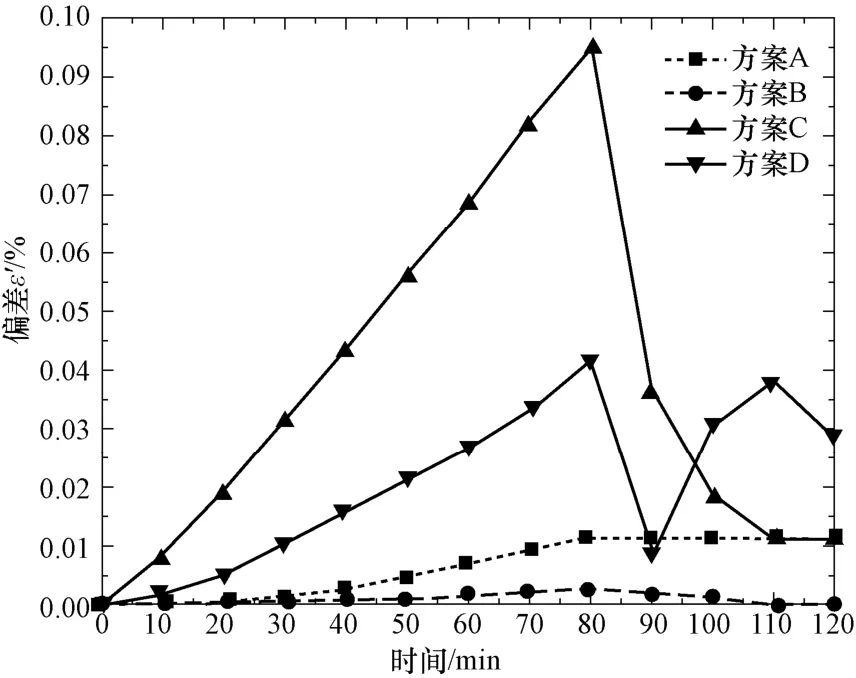
圖8 關(guān)于不良測點的不同處置方案引起的測量偏差Fig.8 Measurement deviation caused by different disposal schemes for a defective measuring point

通過四種方案的比較，本文認為處理不良測點與其他測點代表容積合并時，應(yīng)優(yōu)先考慮相鄰且流動特性相似的合并原則，在流動特性不易判斷時，也可以以相鄰且連通的原則。當擬合并的單元雖相鄰但幾乎不連通，或存在較大干擾源時，可能會引起較大的測量偏差。

5 結(jié)論

本文通過使用ANSYS Fluent 模擬安全殼內(nèi)充氣80 min 并靜置40 min 的打壓試驗過程。基于仿真結(jié)果討論了打壓過程中安全殼內(nèi)流場和溫度場分布以及干空氣質(zhì)量測量方法的可靠性，得到如下結(jié)論：

（1）受殼內(nèi)構(gòu)筑物的影響，無論是在充氣階段還是穩(wěn)壓階段，安全殼內(nèi)的溫度場都不均勻。穩(wěn)壓40 min 后，局部流動較弱的地方溫度比自由空間的溫度仍高2 ℃左右。

（2）空氣質(zhì)量測量值受測點布置和容積分配方案的影響較大。選擇根據(jù)流動和溫度場特性細化后的分配方案，比粗分配方案的測量誤差低0.1%。

（3）對不良測點進行相鄰測點容積合并時，應(yīng)優(yōu)先考慮相鄰且流場相似原則，其次可選擇相鄰且聯(lián)通原則。相鄰但連通性較差、或有溫度場干擾源的區(qū)域合并會導(dǎo)致較大偏差。

致謝

本研究得到了國家重點研究研發(fā)計劃（No.2020YFB1901402）和中國國家自然科學(xué)基金（No.2020YFB1901402）的資助。