穩態“冷源”法對冰的導熱系數測量系統研究*

吳澤龍 程德勝 陶鵬宇 于子麟 竇天陽 游力豪 陳開標 鄭重語

(陸軍炮兵防空兵學院基礎部 安徽 合肥 230031)

冰是自然界中的常見物質,冰的凍結或融化都可能影響含冰系統的傳熱和傳質過程,因此研究含冰系統的熱物性非常重要[1].導熱系數是表征物質熱傳導的物理量,常用材料的導熱系數一般采用實驗的方法得到[2].本文基于穩態法實驗教學儀器和實驗原理進行改進,設計了一套用于室溫環境下測量冰的導熱系數的裝置.

1 測量原理

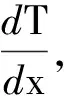
圖1 穩態法測量樣品導熱系數模型

(1)

1.1 熱流量測量原理

如圖2所示,該裝置主要通過下部的半導體散熱器不斷對下銅盤B進行散熱,使得下銅盤溫度在零度以下,上銅盤A直接暴露在空氣中,從空氣中吸收熱量,熱量由上銅盤A流經樣品后從下銅盤散出.當傳熱達到穩態時,對于樣品的任一截面及銅盤A、B,單位時間內流入的熱流量等于流出的熱流量,利用溫度傳感器測量上銅盤A在一段時間內的溫度變化數據并擬合函數求得其在穩態溫度下的熱流量,即流經樣品的熱流量Φ.

圖2 測量裝置結構圖

1.2 溫度梯度測量原理

樣品上下表面溫度及溫度差隨時間變化如圖3所示.

當樣品內部形成穩定的溫度分布狀態時,樣品上下表面的溫度差將趨于定值,樣品表面穩態時的溫度差可通過連續測量上下銅盤的溫度獲得.

由于樣品側面用絕熱材料包裹,如圖4所示,樣品側面與空氣發生的熱交換很小,近似忽略,因此近似認為穩態后樣品內部形成垂直于吸、散熱面的溫度場,那么沿x方向(傳熱方向)的溫度梯度為

圖4 絕熱材料包裹待測樣品圖

(2)

式中T1、T2分別為穩態時樣品上、下表面的溫度,h為樣品厚度,由游標卡尺測得.

2 裝置設計

如圖5所示,圖中數字分別代表:

圖5 實驗裝置示意圖

1——雙路溫度數據采集器;

2——開關電源;

3——半導體散熱器;

4——納米氣凝膠絕熱氈(內包裹待測樣品);

5——銅盤;

6——為Pt100溫度傳感器.

該裝置分為制冷模塊和測溫模塊.其中制冷模塊由半導體制冷器構成,用于給樣品下表面降溫,從而使樣品上下表面形成溫度差;測溫模塊由Pt100溫度傳感器、雙路溫度數據采集器構成,該套裝置測量溫度的最小分度值為0.001 ℃,用于測量并記錄樣品上下銅盤的溫度供熱流量和溫度差的計算及測量.裝置實物圖如圖6所示.

圖6 裝置實物連線圖

3 測量分析

3.1 測量分析

3.1.1 穩態熱流量的測量

將上銅盤A如圖7所示方式放置在與之完全相同且與半導體制冷器緊密貼合的下銅盤B上,并將其降溫至-15 ℃左右(室溫19 ℃),隨后將銅盤A放在相同環境下的納米氣凝膠絕熱氈上,如圖8所示,讓銅盤自然吸熱,利用溫度傳感器每隔1 s記錄一次上銅盤A的溫度,待其升溫至室溫后,停止記錄并導出數據.

圖7 熱流量測量裝置圖

以時間為自變量,溫度為因變量繪制上銅盤A溫度隨時間變化的散點圖如圖9所示.

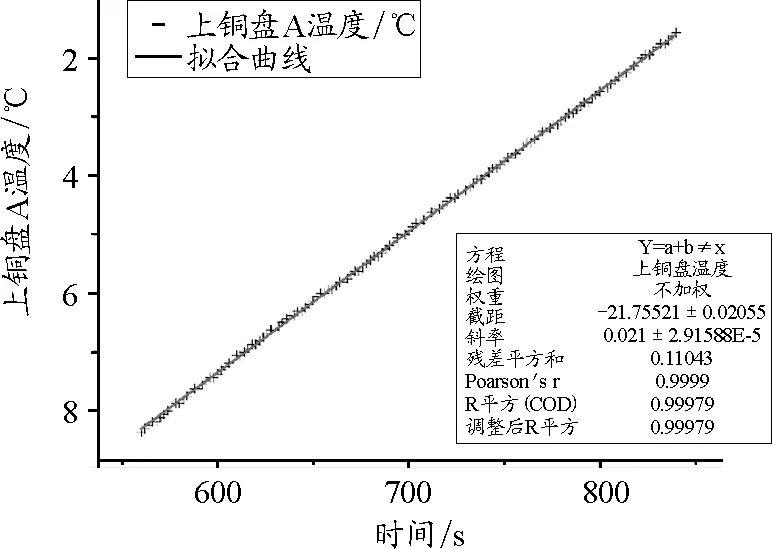
圖9 銅盤A單獨吸熱時的溫度隨時間變化圖

根據圖9所呈現的銅盤溫度隨時間變化趨勢,我們運用一次函數對數據進行擬合,結果表明該方法的擬合優度R2=0.999 79,擬合較好,因此近似認為是上銅盤A在實驗條件下溫度隨時間變化呈線性關系,則銅盤溫度T隨時間t的變化函數

T=kt+b

(3)

又根據吸熱公式

Q吸=cmΔT

(4)

則銅盤吸熱熱流

(5)

其中c為吸熱銅盤的比熱容,m為吸熱銅盤的質量.則聯立公式(3)、(5)可知,實驗過程中流經銅盤的熱流量

(6)

為減小偶然誤差,重復測得5組數據如表1所示.

表1 銅盤單獨吸熱溫度變化率測量數據表

取上述斜率的平均值ˉk作為銅盤的溫度隨時間變化率,將其代入式(6),該熱流量即實驗中流經樣品的熱流量Φ.

3.1.2 樣品厚度和面積的測量

利用游標卡尺在樣品周圍均勻選取5個不同位置的測量點測量上銅盤A上表面到下銅盤B的厚度Hi,由于上下銅盤的厚度均為1.000 cm,樣品厚度

(7)

3.2 實驗結果

為確保測量過程中冰塊樣品的厚度和截面積相同,實驗對同一冰塊樣品采取:降溫至穩態→停止降溫并測量其厚度→再降溫的循環過程,測得如表2所示數據.冰塊樣品直徑測量數據如表3所示.

表2 冰塊樣品厚度及穩態時溫度差測量數據表

表3 冰塊樣品直徑測量數據表

3.3 理想條件下的測量不確定度

假定滿足一維、穩態傳熱條件,則導熱系數的測量不確定度可由熱流量Φ、計量面積S、樣品厚度h和溫差ΔT這4個參數的不確定度合成得到[3].即

(7)

式中:U為測量裝置的不確定度,UΦ為測得穩態時流經樣品的熱流量的不確定度,UΔT為樣品兩側溫度差的不確定度,Uh為樣品厚度的不確定度,US為計量面積的不確定度.

3.3.1 不確定度分量UΦ的評定

A類:由導熱系數測定儀對樣品溫度隨時間變化率隨機的重復測量性引起,由表3數據可得:

算術平均值

(8)

實驗標準差

(9)

標準不確定度

(10)

B類:由于雙路溫度數據采集器溫度示值的最小示數為0.001 ℃,取最小示數的一半作為儀器誤差限Δ儀,按均勻分布考慮,有

(11)

UΦ應由UΦ1、UΦ2合成得到

(12)

同理可求得不確定度分量UΔT、Uh.

3.3.2 不確定度分量US的評定

A類:由游標卡尺對樣品直徑的測量重復性引起.由表2數據可得:

算數平均值

9.88×10-2

(13)

實驗標準差

(14)

直徑d誤差傳導系數

(15)

不確定度

(16)

B類:由于游標卡尺的精確度為0.02 mm,按平均分布,其示值的標準不確定度

(17)

則由示值誤差引起的直徑測量的不確定度

(18)

則計量面積測量的不確定度US應由Ud1、Ud2合成所得

(19)

3.3.3 不確定度的合成

根據以上分析,標準不確定度一覽表如表4所示.

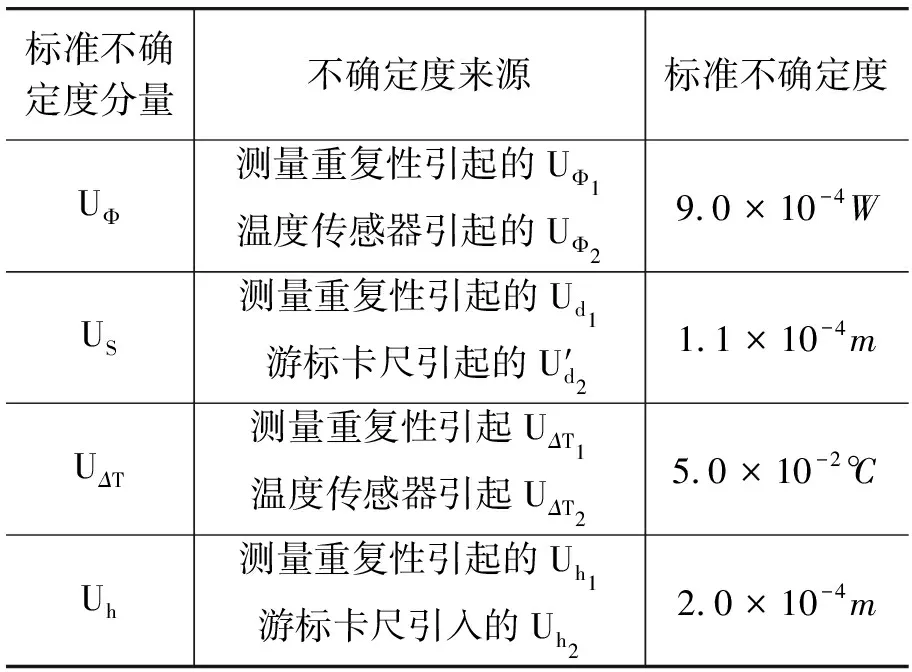
表4 標準不確定度一覽表

其中靈敏度系數為

(20)

(21)

(22)

(23)

代入各靈敏度系數后,計算式為

(24)

代入各最佳值及各不確定度分量后,結果為

U=2×10-1W·m-1·K-1

因此實驗測得冰的導熱系數

λ=(2.1±0.2) W·m-1·K-1

Ur=8%(P=95.5%)

(25)

3.4 測量精度的評定

實驗對制得的6塊冰塊樣品的導熱系數進行了測量,結果如表5所示.

表5 不同冰塊樣品的導熱系數

(26)

由貝塞爾公式,觀測值的中誤差

(27)

相對誤差

(28)

極限誤差

Δ允=2|m|=0.16

(29)

由于在該組實驗中對于不同的樣品而言其外形尺寸都不相同,因此具有隨機性,用樣本誤差估計總體誤差,可得儀器測量的相對誤差優于±4%.

4 誤差分析

4.1 空氣對導熱系數測量的影響

空氣對實驗的影響主要來源于銅盤和樣品間的空氣隙如圖10中框選部分、樣品內部存在的氣泡兩個方面.

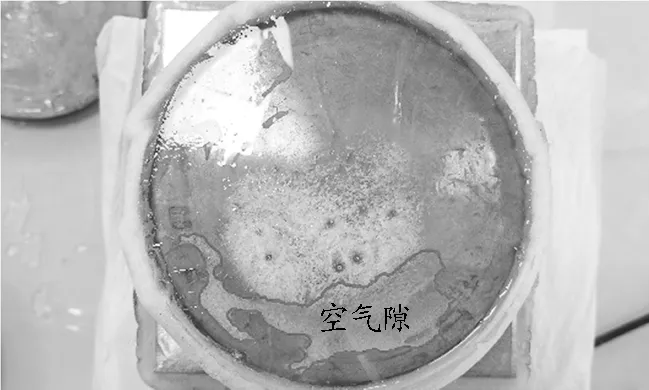
圖10 樣品與銅盤間的空氣隙示意圖

為減小實驗誤差,如圖11所示可通過提前將裝置預冷至接近并略高于樣品熔點,將樣品的一小部分先接觸銅盤,隨后逐漸推至與銅盤對齊,利用樣品略微融化產生的液體填充與銅盤間的間隙,間隙中融化的液體會在散熱器不斷制冷的過程中重新凝固,可有效消除空氣隙.

圖11 冰塊樣品(置于散熱銅盤上)

4.2 雜質對冰的導熱系數測量的影響

由于分子熱運動的存在,雜質對冰導熱系數的影響不可避免.本實驗將食鹽和淀粉作為雜質的代表探究其對冰的導熱系數的影響.通過配置梯度質量分數的食鹽溶液和淀粉凝膠凍結成樣品測量其導熱系數,實驗得到了一系列不同質量分數下樣品的導熱系數,實驗數據及散點圖如表6、表7和圖12、13所示.

表6 淀粉濃度與導熱系數關系測量數據

表7 食鹽濃度與導熱系數關系測量數據

圖12 淀粉雜質對冰的導熱系數的影響

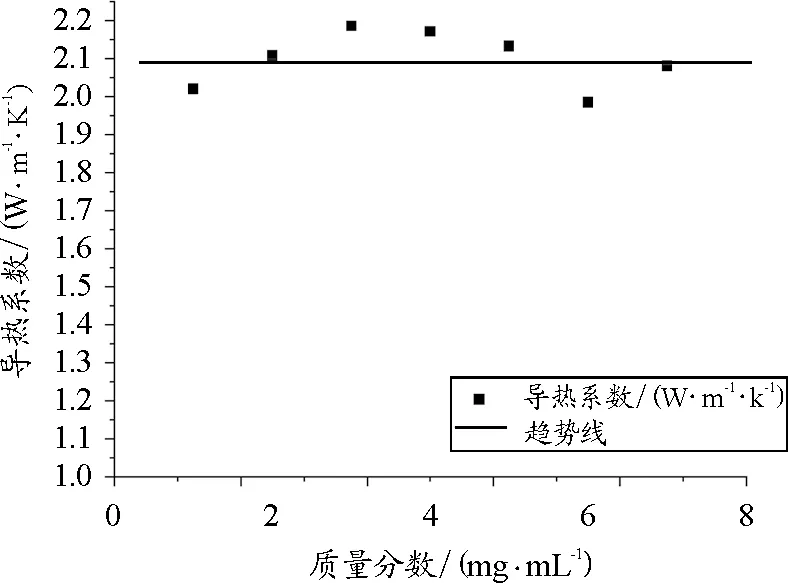
圖13 食鹽雜質濃度對冰的導熱系數的影響

由表6、表7數據可以看出,在實驗范圍內摻入雜質的樣品的導熱系數與相對純凈的冰塊的導熱系數較為接近,這與冰的性質密切相關.由于冰是單礦巖,不能和其他物質結晶,所以水在結晶過程中,會自動排除雜質,因此摻入雜質的樣品實質上是由純凈的冰和摻入的雜質混合而成的.故本組驗結果表明:少量雜質并不會對冰的導熱系數造成較大影響.

4.3 樣品平均溫度對導熱系數的影響

由于熱傳導實質是物質中大量的分子熱運動,樣品平均溫度對測量結果可能有一定影響.本組實驗通過改變樣品的平均溫度并測量樣品在該溫度下樣的導熱系數的方法探究實驗,測得結果如表8和圖14所示.

表8 室溫及該溫度下樣品的導熱系數

圖14 溫度及溫度差與冰導熱系數關系圖

從圖14可以看出,當樣品溫度變化在±3 ℃時溫度對導熱系數的影響優于7%,因此小范圍的溫度波動對于測得的冰的導熱系數結果影響較小.

需要指出的是:由于冰是分子晶體,其導電性很弱,因此在忽略電子對熱傳導貢獻的情況下,冰中的熱傳導主要依靠聲子來完成.此時冰的導熱系數的微觀表達式為

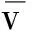
查閱資料可知:當T?ΘD(ΘD為德拜溫度)時,起作用的是聲子碰撞的倒過程,必須有短波參與才有可能發生[4].

當T?ΘD時,溫度升高平均聲子數增大,相互“碰撞”的幾率增大,自由程減小.這時平均自由程l和溫度成反比,而晶格熱容與溫度無關,此時冰的導熱系數與溫度成反比.

5 結束語

(1)本文基于穩態法設計了一套測量冰的導熱系數的實驗裝置,系統包括制冷模塊和測溫模塊,能在室溫下準確測量冰的導熱系數.

(2)相比于常見的導熱系數測量裝置,本裝置的技術優勢在于使用“冷源”替換“熱源”,可在保持含冰物質狀態穩定的情況下研究其熱物性,且裝置結構簡單,無流動工質,可有效降低研究門檻,有利于廣泛開展對冰的有關性質的研究.

(3)針對測量過程中可能存在的空氣隙、樣品溫度以及雜質對樣品導熱系數測量的影響,本文給出了可供參考的解決方案并通過設計實驗研究了相關因素對實驗測量的影響,實驗證明少量的雜質和較小的樣品溫度變化對實驗測得數據的影響較小,裝置對數據的測量具有良好的可重復性,測量結果較為可靠.

(4)作為大學物理實驗的教學內容之一,本文探索性地利用現有儀器加以改造解決了測量冰的導熱系數的問題,是拓寬物理實驗教學內容適用范圍的成功范例.