FSAE賽車懸架的設計與研究

安嘉晨，臧利國*，陳博文,2，錢 程，柏宇星

FSAE賽車懸架的設計與研究

安嘉晨1，臧利國*1，陳博文1,2，錢 程1，柏宇星1

（1.南京工程學院 汽車與軌道交通學院，江蘇 南京 211167； 2.北汽重型汽車有限公司，江蘇 常州 213133）

基于大學生方程式汽車大賽（FSAE）比賽規則，分析了比賽對賽車懸架性能的要求，計算了相關的動力學參數，確定了懸架系統的形式并使用CATIA進行建模。在ADAMS中構建了懸架的運動學模型，并分析了懸架模型在輪跳分析時相關性能指標參數的變化范圍。仿真結果表明，所設計的懸架系統滿足規則要求，但車輪定位參數隨車輪上下跳動時的變化幅度較大，不利于操縱穩定性。然后在ADAMS/Insight中基于車輪的定位參數對模型的硬點坐標進行試驗設計（DOE）分析優化，優化前后的結果對比表明，優化后車輪跳動時車輪定位參數的變化量顯著減小，賽車的性能得到了很好的改善。

FSAE；懸架系統；車輛運動學仿真

懸架是大學生方程式賽車的重要組成部分之一，國內外各大高校與汽車生產廠商均給出了許多不同的懸架設計布置方案。石璇等[1]在設計懸架彈簧布置方式時，選取了雙橫臂搭配第三彈簧的設計結構，并借助第三彈簧完成解耦。劉凱華等[2]采用了互聯雙橫臂獨立懸架的結構設計，使得車輪定位參數在一定范圍內得到有效控制，從而保證車輛良好的操縱穩定性。王樂等[3]使用了多連桿式懸架，該懸架的空間自由度更為靈活，能為賽車提供更大的橫向及側向剛度，給予輪胎更好的抓地力。王德朝等[4]在CATIA建立了不等長雙橫臂前懸架模型，并把模型拆解為各個運動副做剛性連接，以簡化建模過程。鄧健賢等[5]利用ADAMS/Car建立懸架系統模型，先利用MATLAB制作一個設計界面，得出所有懸架系統參數后在ADAMS中構建最終模型。陳剛等[6]在建立前懸架運動學模型時做了若干簡化和假設，將懸架簡化為一個多連桿機構，假設其零部件連接不考慮間隙，各運動副視為剛性連接，減震器阻尼特性為線性，車輪上下跳動時不考慮車身運動。吳振昕等[7]結合數值計算方法和空間機構運動學建立了雙橫臂獨立懸架運動學模型，并對懸架的K&C特性進行了仿真計算。張建等[8]在分析懸架的運動響應時，設計了一種基于車輛加速度的懸架行程解耦算法以及一種通過懸架運動行程判別路面不平度的算法，并進行了道路試驗驗證該方案的可行性。SINDHWANI等[9]借助SolidWorks自主設計搖臂和橫臂，以改善人體工程學設計，通過早期整車參數估算整車重量，并推算每個車輪所分得的質量進而推算整車的質心位置。BALENA 等[10]借助多系統耦合仿真將懸架、轉向、制動等輸入全部設置在同一物理環境下進行模擬，并將懸架與底盤視作剛體，以減少仿真時的工作量。本文以國內外高校大學生方程式賽車懸架系統的研究為支點，確定一套懸架系統的設計和選型方案。完成設計后將模型導入ADAMS中進行相關的運動學仿真及優化，以改善設計的合理性及實用性。

1 懸架結構的設計與選型

懸架系統在設計初期需要考慮大量因素，包括但不限于整車基本參數、各系統質心分布、懸架布置形式、懸架硬點參數、懸架剛度計算、傳遞比和載荷計算、懸架零部件設計等。

1.1 懸架的基本設計思路

懸架的基本設計思路如圖1所示。

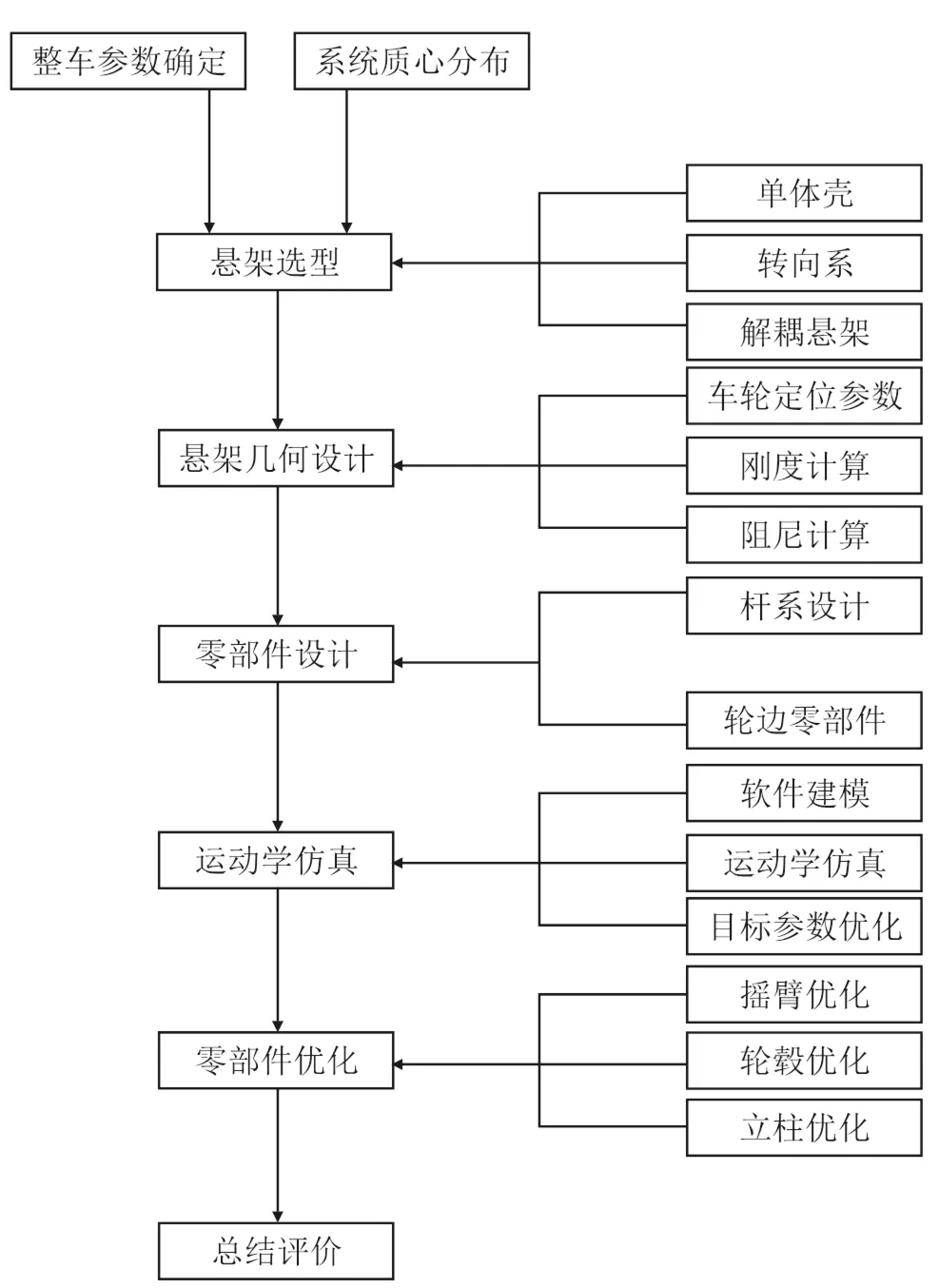
圖1 懸架設計技術路線圖

1.1.1確定基本參數

根據賽車已知的整車基本參數，在確定好發動機與傳動系的空間位置關系后，確定輪距、軸距等基本參數。取設計軸距為1 700 mm；前輪距為1 270 mm；后輪距為1 240 mm。

1.1.2確定各子系統質量分布

本文借助虛擬樣機規劃整車各系統質量分布和前后軸的載荷配比，最終確定各系統的空間位置和質量分布。已知整車的設計滿載質量約為330 kg，同時根據計算得到質心距前軸距為933.53 mm，質心距后軸距為766.47 mm。簡單計算可知前后軸載荷比分別為45%和55%，符合大學生方程式賽車的設計思路。

1.2 懸架的選型

根據大學生方程式汽車大賽（Formula Society of Automotive Engineers,FSAE）比賽規則，賽車必須裝有可自由工作、帶有減震器的懸架；且懸架行程不得小于50 mm，當車手坐進賽車時能保證輪邊有上下25 mm的輪跳范圍[11]。綜合考慮空間布置、成本計劃等因素，雙橫臂式懸架是最理想的結構方案。

由于賽車將采用半單體殼的設計方案，且綜合考慮到懸架系統的重心及彈性元件外部的空間布置等因素，前懸架擬采用雙橫臂直推式懸架，借助防傾桿來增加側傾剛度。后懸擬采用雙橫臂雙彈簧解耦懸架，用一根斜置彈簧控制側傾剛度，另一根橫置彈簧控制俯仰剛度。

1.3 懸架幾何參數設計

1.3.1車輪定位參數

車輪定位參數包括車輪外傾角、主銷后傾角、主銷內傾角及車輪前束角。初步擬定車輪定位參數如表1所示，通過設定基本車輪定位參數來建立懸架硬點坐標，后期根據車輪定位參數變化范圍進行懸架硬點參數優化。

表1 初步擬定車輪定位角參數 單位：(°)

參數主銷內傾角主銷后傾角車輪外傾角車輪前束角 前懸41-1-1 后懸1.952.4500

1.3.2剛度計算

在計算懸架剛度之前需要先確定懸架的偏頻，通常大學生方程式賽車的偏頻在2.4～4 Hz之間，并使前懸架略大于后懸架。根據公式計算并暫取前后懸架的偏頻f=3.2 Hz、r=2.8 Hz；計算前后軸單側載荷（去除車手質量），得f=58.5 kg、r=71.5 kg；計算前后軸懸架適乘剛度，得RF= 23 649.15 N/m、RR=22 130.02 N/m。

車輪中心剛度指的是車輪中心相對車架垂直位移所受的垂向力，賽車擬采用13英寸輪胎，取徑向剛度T=100 700 N/m，根據式（1）、式（2）求解前后懸架車輪中心剛度WF、WR：

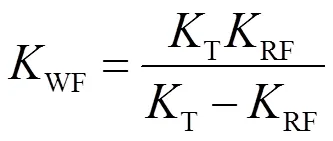
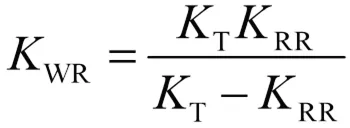
根據計算結果，選取前后車輪中心剛度WF、WR分別為30 909 N/m、28 363 N/m。

為研究整車在轉彎時懸架的運動場景，需要計算車身在經過單位轉角扭轉時總的彈性恢復力矩，根據式（3）、式（4）計算前后懸架側傾角剛度KF、KR：

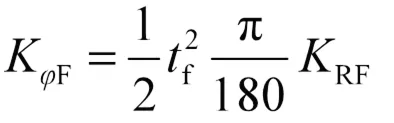
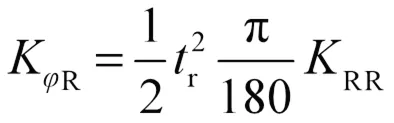
式中，f為前輪輪距，取1.27 m；r為后輪輪距，取1.24 m。計算得出前后懸架側傾角剛度KF、KR分別為435.1 Nm/(°)、380.58 Nm/(°)。

考慮到賽車在場地內轉彎工況的模擬，假設賽車以=40 km/h的速度過彎，轉彎半徑為9 m，根據式（5）計算轉向時橫向加速度A為1.4。

A=2/() （5）

但在很多情況下，賽車轉彎工況貼近以1的橫向加速度過彎，賽車其以1的橫向加速度過彎時車架和車身側傾轉角的大小被稱之為側傾增益，根據式（6）計算側傾增益。

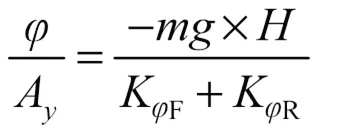
式中，為車身側傾角；為質心到側傾軸線距離，取0.25 m，代入參數計算得側傾增益為-1.11 (°)/g；一般大學生方程式賽車的側傾增益約在1.0～1.8(°)/g，計算得出的1.11(°)/g在目標參數合理置信區間內，考慮到前懸架采用直推式懸架，會需要更多的側傾角剛度，故擬添加防傾桿。

由于轉彎產生了橫向加速度，從而導致側向發生了力的偏移，稱為載荷轉移。根據式（7）、式（8）計算前后軸因橫向加速度所引起的載荷轉移。

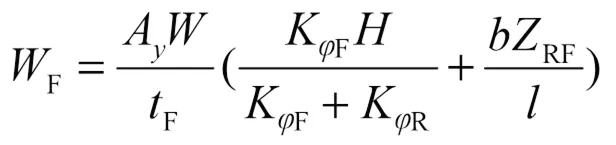
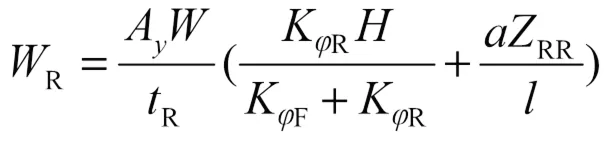
式中，RF、RR分別為前后懸架靜態側傾中心高度，分別取-6.4×10-3m、-4.4×10-3m；計算載荷轉移F、R分別為468 N、436 N。至此，根據載荷轉移反算懸架適乘剛度和懸架偏頻以證明擬定偏頻設計合理。

通過懸架幾何結構確定前后懸架的傳遞比1=1.2、2=1.3；計算前后懸架的彈簧剛度得SF=44 508.96 N/m、SR=47 933.47 N/m；計算前后懸架彈簧的實際行程得SF=SR=0.02 m。

根據上述行程、剛度等計算挑選減震器彈簧，擬選擇型號RCP2S-190的山地車減震器，可調磅數550 lbs，磅數調節范圍方便后懸架解耦策略，需實車落地后調節預載荷來實現完全解耦。

1.3.3阻尼計算

在選擇好目標減震器彈簧后，根據其設計生產參數計算減震器的阻尼系數：

2s=4s（9）

式中，為相對阻尼系數；s為簧上質量，kg；為懸架偏頻，Hz。

減震器的相對阻尼系數決定了其減震效果，一般彈簧在設計時會把壓縮時的相對阻尼系數b取得更小，回彈時的相對阻尼系數r取得更大，即減震器在壓縮過程中的減震效果不如回彈時的減震效果明顯；在取b、r的時候，取平均相對阻尼系數a討論取值范圍。對于無內摩擦的彈性元件懸架，取a=0.25～0.35，而在有內摩擦的彈性元件懸架，a會取得略大；綜合考慮后，確定壓縮和回彈阻尼相對系數a=0.3、r=0.4。

根據式（10）－式（13）計算前后懸壓縮、回彈阻尼系數BF、RF、BR、RR：

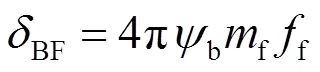
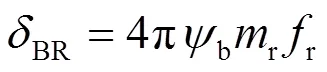
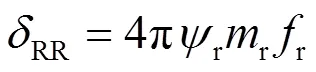
將之前計算的前后軸單側載荷f、f，前后懸架偏頻f、r代入方程計算可得：前懸壓縮回彈阻尼系數分別為705 Ns/m、941 Ns/m；后懸壓縮回彈阻尼系數分別為617 Ns/m、823 Ns/m。

1.4 懸架零部件設計

1.4.1桿系設計

1.橫臂、推桿設計

在設計懸架橫臂時，需考慮桿系的尺寸選擇以及連接方式：從不同工況下懸架橫臂的應力和變形情況以及加工的難易程度來考慮桿件的尺寸設計；綜合考慮后，擬采用外徑16 mm壁厚1.5 mm的鋼管作橫臂，配合螺紋焊接套、桿端軸承及吊耳焊接。并用12.9級M8塞打螺栓配合M6防松螺母對橫臂與立柱、車架安裝點進行裝配與連接。

因前懸架為直推式，當賽車靜置于地面時，推桿多受到軸向力，故可適當減小推桿尺寸來減少懸架系統的整體質量；采用外徑14 mm壁厚1.5 mm鋼管配合螺紋焊接套進行焊接。

2.防傾桿、搖臂設計

擬通過設計U形防傾桿增加前懸架側傾角剛度。防傾桿通過搖臂與連接桿、扭臂、扭桿把左右懸架連接，將防傾桿布置在車內底板，借助預埋件進行吊裝，合理布置空間。防傾桿的裝配如圖2所示。

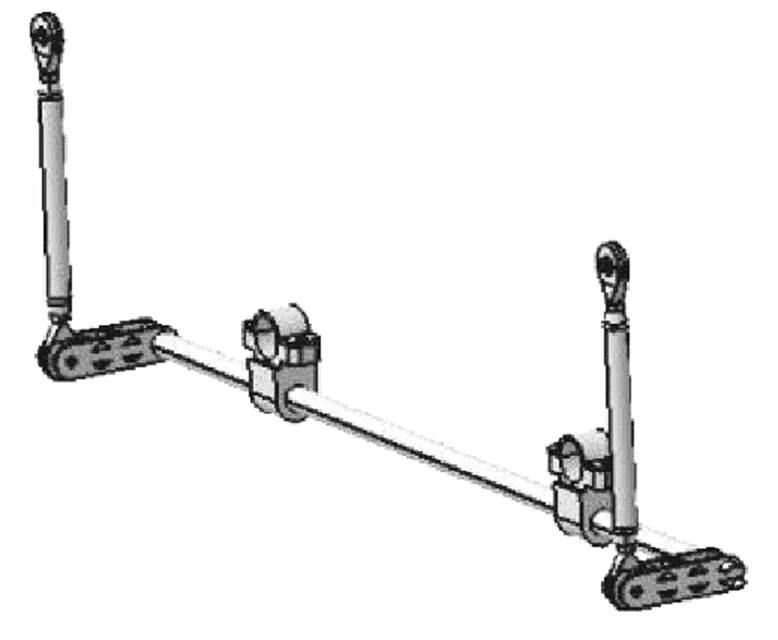
圖2 防傾桿裝配模型

根據空間硬點圖設計搖臂外形，借助塞打螺栓和防松螺母連接各點，并根據有限元軟件仿真分析，在保證搖臂基本結構性能的情況下適當減料，以達到懸架系統輕量化的目的。

3.桿系裝配

桿系設計完成后在CATIA中進行整體裝配，并在運動模擬分析模塊（DMU）驗證懸架桿系運動范圍以及合理性。將減震器模型、搖臂、防傾桿、扭桿、推桿、橫臂、吊耳等依次連接，最終得到桿系裝配如圖3所示。

圖3 前懸架桿系裝配模型

1.4.2輪邊零部件設計

輪邊的正向設計思路為優先考慮制動系，并計算發動機至差速器、傳動軸極限轉速來對軸承尺寸選型；同時考慮轉向系，確定立柱的大致輪廓和關鍵節點，在確定好上下橫臂的安裝點后設計其安裝方式；通過查閱資料確定軸承類型及型號，方便后期端蓋、保護罩、缸套的選型和設計；然后是轉向吊耳位置的設計，轉向吊耳的高度應優先考慮轉向梯形的布置；最后再考慮輪速傳感器的安裝位。

1.立柱及輪轂設計

立柱在輪邊零部件中最為重要，其具備為轉向拉桿提供連接點、為制動卡鉗提供安裝點、設置軸承安裝座、保證懸架橫臂硬點的安裝、設置傳感器安裝點等多項功能。立柱屬于簧下質量部分，在設計中對其進行空間拓撲優化分析，可去掉部分結構以適當減小其質量。輪轂通過螺栓和輪輞連接，其運動規律與輪輞相互綁定；同時還具有安裝制動盤的功用。其中后輪轂需借助三球銷和花鍵軸傳遞半軸的力和力矩，同時可設計鋼套減少三球銷與輪轂的直接磨損。

2.輪邊裝配

完成設計后，用CATIA的DMU模塊檢查無機械干涉即可。將輪邊所有零部件進行裝配，包括但不限于：立柱、輪轂、端蓋、剎車盤、輪輞、輪胎、軸承等，具體裝配效果如圖4所示。

圖4 輪邊總裝模型

2 懸架系統的動力學建模與仿真

2.1 懸架系統運動學建模

在確定好懸架系統的總體設計后，在ADAMS/ Car模塊中建立懸架模型并添加運動副，最終建立的模型如圖5所示。

圖5 解耦懸架模型

2.2 懸架系統運動學仿真

FSAE規則規定：在有車手乘坐的情況下，賽車輪胎的跳動行程至少為50 mm[11]。所以在建模完成后切換至ADAMS/View模塊，預設輪胎空載時的車輪自由半徑為250 mm；車輪胎端面寬度為200 mm；扁平率為45%；垂向剛度為200 kN/m；徑向剛度為190 kN/m。分別對懸架進行靜載、平行輪跳、單側輪跳分析。

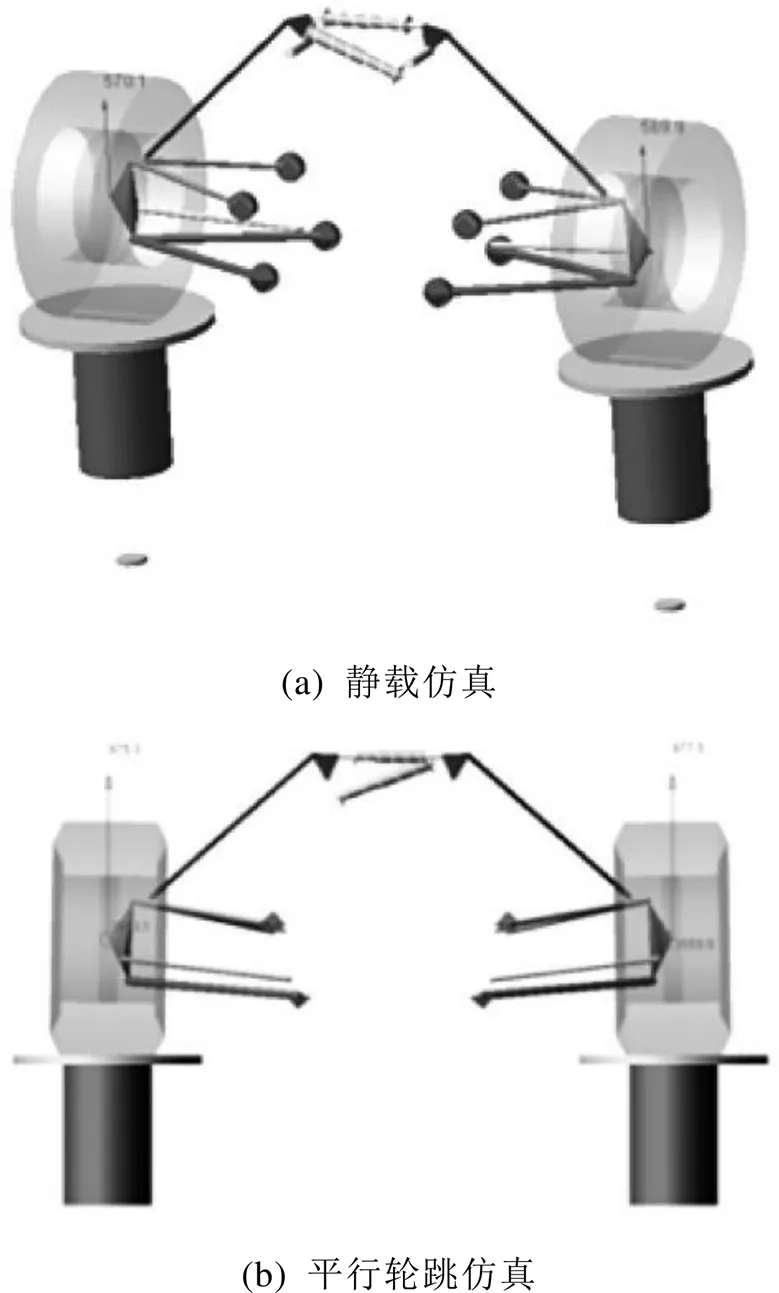
進入靜態載荷仿真模塊，由靜載仿真結果可知當空載時，輪邊立柱受到的力約為570 N，方向垂直地面向上，符合預期，受力分析如圖6(a)所示。

為模擬賽車在起步或制動時的后仰和點頭情況，對賽車進行平行輪跳仿真；根據規則要求設計輪跳行程為±25 mm的仿真條件，觀察減震器和搖臂的運動狀況。受力以及力矩情況如圖6(b)所示。

當賽車以1.4的加速度過彎時，需要驗證懸架系統的可靠性，設置單側輪跳工況分析來模擬過彎時的懸架運動過程。觀察懸架運動規律并分析解耦懸架中彈簧的實際運動方式。單側輪跳分析時，單側輪處于+25 mm位置時立柱的受力及力矩情況如圖6(c)所示，結果證明懸架系統可靠性良好。

2.3 輪胎定位參數分析

將硬點參數進行平行輪跳仿真試驗的數據進行后處理并利用ADAMS/Insight模塊作圖分析，橫坐標為輪跳行程，縱坐標為對應車輪定位參數角變化；因車輪上下跳動工況一致，為優化仿真設置并減少計算步驟，主要以正輪跳部分作為仿真行程設置，具體分析如圖7所示。

如圖7(a)所示，懸架設計硬點參數在平行輪跳時引起的車輪外傾角變化為0～?1°。處于靜平衡位置時外傾角為0°，變化率為0.9(°)/25 mm。

如圖7(b) 所示，懸架設計硬點參數在平行輪跳時引起的主銷后傾角變化為2.4～?2.95°。處于靜平衡位置時主銷后傾角為2.45°，變化率為0.5(°)/ 25 mm。

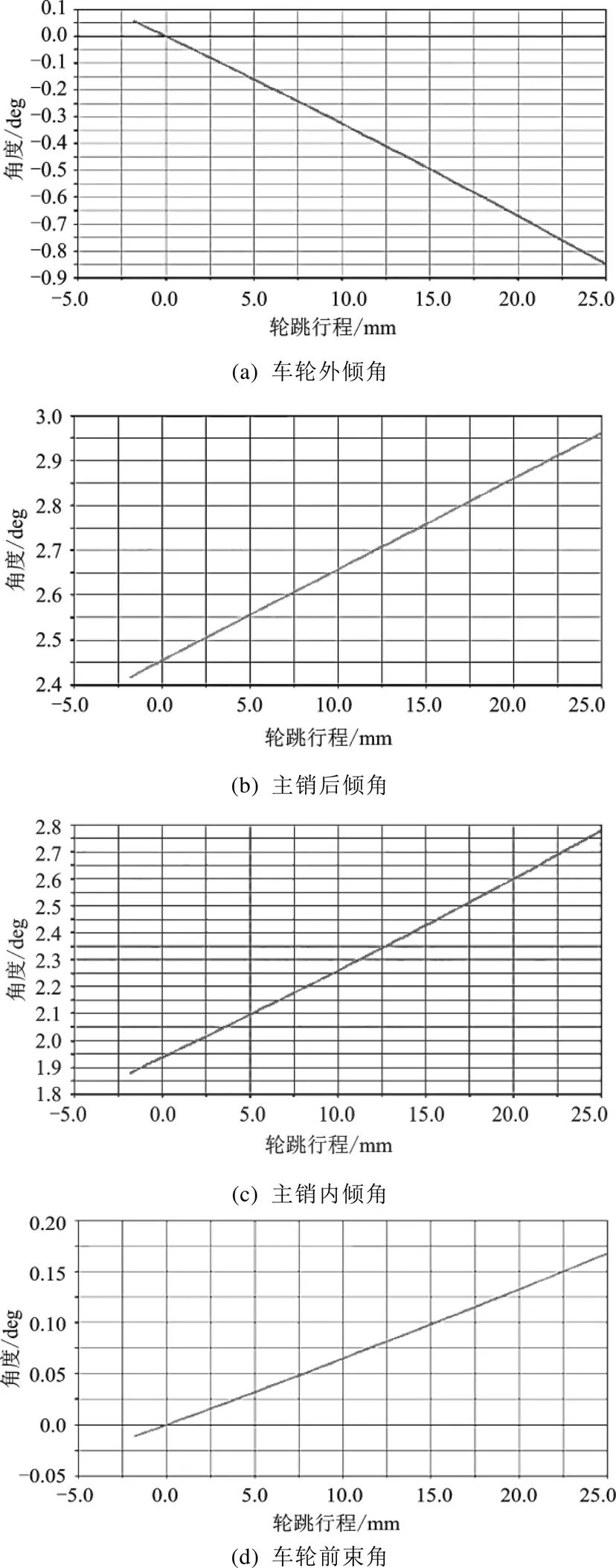
圖7 平行輪跳下車輪定位參數變化示意圖

如圖7(c)所示，懸架設計硬點參數在平行輪跳時引起的主銷內傾角變化為1.9～?2.7°。處于靜平衡位置時主銷內傾角為1.945°，變化率為0.83(°)/ 25 mm。

如圖7(d)所示，懸架設計硬點參數在平行輪跳時引起的前輪前束角變化為0～0.17°。處于靜平衡位置時車輪前束角為0°，變化率為0.17(°)/ 25 mm。

3 懸架系統運動學優化

在進行輪胎定位參數的分析后，需進一步利用ADAMS/Insight模塊進行試驗設計（Design Of Experimen, DOE）優化分析，通過設置優化參數、目標參數以及優化方法和權重來實現對懸架的目標參數優化。

3.1 目標參數優化設置

通過修改懸架硬點坐標來進行車輪定位參數的優化，考慮到懸架系統與車架的連接點已經確定，車輪輪距、軸距等參數基本無法修改。因此，在設置的過程中，不會對硬點的坐標進行修改。因為左右懸架對稱設計，故選取單邊作為研究對象，擬挑選上下橫臂前點和后點的坐標及坐標、導向桿內點坐標及坐標作為參數優化的變量，四個車輪定位參數作為目標優化值。

設置參數后即可進入Insight模塊進行參數優化，設定變量變化范圍在±3 mm之內，計算方式采用線性計算，初步擬定4個目標參數優化權重均為1.0。優化前后四個定位角參數如表2所示。

表2 優化前后車輪定位角參數對比 單位：(°)

參數主銷內傾角主銷后傾角車輪外傾角車輪前束角 優化前1.952.4500 優化后2.712.720.770.05

3.2 優化后硬點參數DOE分析對比

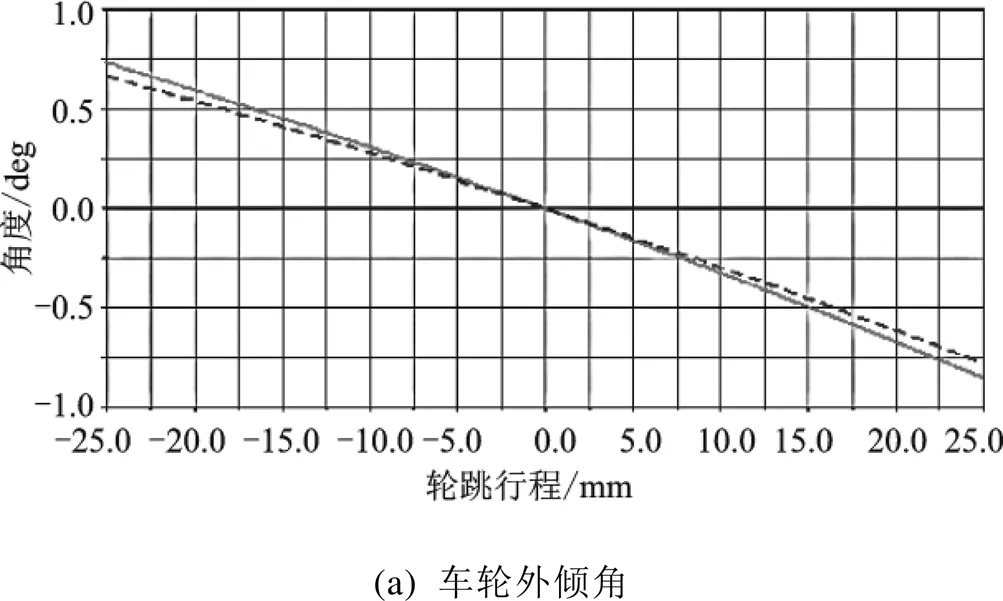
將優化后硬點參數進行單側輪跳仿真試驗的數據進行后處理，直接在原車輪定位參數的數據圖上添加優化后的變化曲線，如圖8所示。

如圖8(a)所示，優化后的懸架設計硬點參數在單側輪跳時引起的車輪外傾角變化為?0.7～0.75°。處于靜平衡位置時，車輪外傾角為0°，變化率為1.45(°)/50 mm。經DOE分析優化后，整體變化范圍減小，實現參數優化目標。

如圖8(b)所示，優化后的懸架設計硬點參數在單側輪跳時引起的主銷后傾角變化為2.2～2.7°。處于靜平衡位置時，主銷后傾角為2.45°，變化率為0.5(°)/50 mm。經DOE分析優化后，整體變化范圍減小，實現參數優化目標。

如圖8(c)所示，優化后的懸架設計硬點參數在單側輪跳時引起的主銷內傾角變化為1.25～2.75°。處于靜平衡位置時，主銷內傾角為1.95°，變化率為1.5(°)/50 mm。經DOE分析優化后，整體變化范圍減小，實現參數優化目標。

如圖8(d)所示，優化后的懸架設計硬點參數在單側輪跳時引起的車輪前束角變化為?0.15～0.15°。處于靜平衡位置時，車輪前束角為0°，變化率0.3(°)/50 mm。因后懸架無轉向機構，僅設置導向桿用于約束車輪隨動轉向，圖中縱坐標表示的束角變化范圍變化值小于0.5°，屬于合理變化范圍。

4 總結

1）基于FSAE比賽規則并采用正向設計思路提出了一套大學生方程式賽車懸架系統的設計方案，根據整車的布置特點確定了懸架具體的幾何參數，進行了懸架設計參數的計算及構件選型，并在CATIA中進行了建模。

2）在ADAMS/Car和ADAMS/View中建模并分析了懸架的運動學性能，仿真的結果表明，所設計的懸架系統滿足比賽規則要求。

3）在ADAMS/Insight中基于車輪的定位參數對懸架的硬點坐標進行了DOE分析優化。優化前后仿真結果的對比表明，優化后車輪跳動時賽車的性能得到了很好的改善。

4）在后期懸架的實際制造及調試過程中已對模型構建方法及仿真分析數據進行了相關驗證，證明了本文所述內容的合理性。

[1] 石璇,葉胤欣,彭育輝.基于第三彈簧結構的前懸架俯仰運動分析[J].時代汽車,2020(8):79-82.

[2] 劉凱華,王慶,李強.裝有互聯雙橫臂獨立懸架的方程式賽車仿真分析[J].浙江科技學院學報,2019,31(3): 239-246,252.

[3] 王樂,朱建軍,田宇.大學生方程式賽車多連桿懸架設計及優化[J].機械設計與制造,2018(2):9-12.

[4] 王德朝,丁華鋒,孟凡凈,等.FSEC賽車前懸架系統仿真與優化[J].重慶理工大學學報(自然科學),2018,32 (4):21-26.

[5] 鄧健賢,查云飛.大學生方程式賽車懸架系統設計[C]//2021中國汽車工程學會年會論文集.北京:機械工業出版社,2021:6.

[6] 陳剛,曹永青.基于 ADAMS 的大學生方程式賽車前懸架設計與優化[J].三明學院學報,2017,34(6):33-38.

[7] 吳振昕,付振,程超,等.基于運動學特性的雙橫臂懸架硬點位置優化[J].汽車技術,2015(2):39-43.

[8] 張建,劉秋錚,王康,等.基于懸架行程解耦的SUV路面不平度識別算法研究[J].汽車工程,2016,38(10): 1232-1236,1199.

[9] SINDHWANI R,BHATNAGAR A,SONI A,et al. Design and Optimization of Suspension for Formula Society of Automotive Engineers (FSAE) Vehicle[J]. Materials Today,Proceedings,2021,38:229-233.

[10] BALENA M,MANTRIOTA G,REINA G.Dynamic Handling Characterizationand Set-up Optimization for a Formula SAE Race Car via Multi-body Simulation [J].Machines,2021,9(6):126.

[11] 李理光.中國大學生方程式汽車大賽規則[Z].北京:中國汽車工程學會,2022.

Design and Research of FSAE Racing Suspension

AN Jiachen1, ZANG Liguo*1, CHEN Bowen1,2, QIAN Cheng1, BAI Yuxing1

( 1.School of Automobile and Rail Transit, Nanjing Institute of Technology, Nanjing 211167, China; 2.BAIC Heavy Truck Company Limited, Changzhou 213133, China )

Based on the formula society of automotive engineers(FSAE) competition rules, the requirements of the race on the suspension performance of the racing car are analyzed, the relevant dynamic parameters are calculated, the form of the suspension system is determined and modeled in CATIA. In ADAMS, the kinematics model of the suspension is constructed, and the variation range of the relevant performance index parameters of the suspension model during the wheel jump analysis is analyzed. The simulation results show that the designed suspension system meets the requirements of the rules, but the wheel alignment parameters change greatly with the vertical displacement of the wheel, which is not conducive to the handling stability. In ADAMS/Insight, the design of experimen (DOE) analysis and optimization of the hard point coordinates of the model are carried out based on the positioning parameters of the wheels. The comparison results show that the amount of change in wheel alignment parameters when the wheel runout after optimization is significantly reduced, and the performance of the car is well improved.

FSAE; Suspension system; Vehicle kinematics simulation

U469.6+96

A

1671-7988(2023)20-51-08

10.16638/j.cnki.1671-7988.2023.020.011

安嘉晨（2000－），男，研究方向為汽車動力學，E-mail:1426547879@qq.com。

臧利國（1986－），男，博士，教授，研究方向為車輛系統動力學與控制，E-mail:zangliguo1986@163.com。

江蘇省大學生實踐創新訓練計劃項目（202111276027Z）；南京工程學院科研基金（CKJA202205）。