基于高階間斷伽遼金數值方法的浸沒邊界法

王婷婷，呂宏強，安 慰

(南京航空航天大學 航空學院，南京 210016)

0 引言

浸沒邊界法（immersed boundary method,IBM）最初由Peskin 于1972 年[1]提出，用于心臟瓣膜周圍流動的模擬。在該方法中[1-2]，流體在笛卡爾網格上求解，幾何體被一組拉格朗日點所取代，通過在控制方程中添加源項實現邊界對流體的作用，如Lee[3]和Nicolaou[4]所述，這類IBM 稱為連續強迫IBM。自從IBM 提出以來，該方法得到了巨大的發展并廣泛應用。Mohd-Yusof[5]和Fadlun 等[6]提出了直接強迫IBM，與連續強迫IBM 不同的是，不使用拉格朗日點并且強迫項在笛卡爾網格上直接進行計算，控制方程僅僅在流體域的計算網格上求解。何躍龍等[7]引入Choi 等[8]提出的指數插值法對目標點速度進行插值，建立了適用于可壓縮流動的浸沒邊界法。Yang等[9]采用大渦模擬與浸沒邊界相結合的方法，對后向臺階流動進行了數值模擬。Giannenas 和Laizet[10]提出了一種基于三次樣條重建的浸沒邊界方法，用于基于笛卡爾網格的湍流中浸沒物體的高保真模擬。Kou等[11]提出一種基于體積懲罰的結合高階通量重建方法的浸沒邊界法。盡管IBM 已得到廣泛應用，但采用笛卡爾網格結合高階方法的探索仍較少。

近年來，間斷伽遼金（discontinuous Galerkin,DG）方法已成為CFD 中最有前途的高階離散技術之一[12-13]。1997 年，Bassi 和Rebay 等[14-15]采用DG 方法求解了歐拉方程和N-S 方程，隨后Bassi 等[16]又將DG 方法拓展到可壓縮流和不可壓縮流的DNS（direct numerical simulation）和ILES（implicit large eddy simulation）。Landmann[17]在其博士論文中發展了并行高階DG 方法并對二維N-S 方程及RANS（Reynolds-averaged Navier-Stokes）方程進行了求解。DG 方法在國內起步較晚，蔚喜軍和周鐵[18]在2005 年采用龍格-庫塔間斷伽遼金（Runge-Kutta discontinuous Galerkin,RKDG）方法求解了二維可壓縮歐拉方程。于劍和閻超[19]通過引入全局提升算子和局部提升算子，發展了求解N-S 方程的DG 方法的一般框架。張來平等[20]發展了DG/FV 混合方法，計算效率相較于同階精度的DG 方法更高。黨亞斌等[21]發展了一種基于解析精確Jacobian 矩陣的GMRES隱式方法，用于求解可壓縮層流及湍流問題，提高了隱式高精度DG 方法的計算穩定性和計算效率。國外已有研究者將DG 方法與浸沒邊界法相結合，但大多采用切割網格的方法。針對基于笛卡爾網格的浸沒式幾何體，Qin 等[22]提出了一種求解歐拉方程的DG 方法。Müller等[23]提出了一種高階離散格式，用于求解具有浸沒邊界的可壓縮歐拉和N-S 方程，在一個由水平集函數隱式定義的域中使用DG 離散化，采用了一種非侵入式單元聚集技術。雖然切割網格法對于靜態邊界能夠較好的實現，然而切割網格法僅限于低精度，而且小切割單元的處理以及動態邊界的處理比較復雜。

本文引入Kou 等[11]提出的基于體積懲罰的浸沒邊界實現思路，提出基于懲罰項模式的高階DG 浸沒邊界法，采用典型算例對所提出方法進行測試驗證。

1 控制方程

可壓縮黏性流體的控制方程[17]寫成：

式中：U為守恒變量；Fi為無黏通量；Fv為黏性通量。

2 間斷伽遼金空間離散

因為式（1）中存在2 階偏導數項，在求解前必須對方程進行降階處理。采用Landmann[17]使用的混合方法，在計算中把1 階偏導數項當作額外變量，引入輔助變量 Θ。式（1）可以改寫成如下形式：

采用間斷伽遼金有限元法對式（2）和式（3）進行空間離散。在式（2）和式（3）的兩邊同乘一個任意的測試函數W，并將測試函數的高階表達式代入，在計算域單元邊界上的積分中引入逆風格式，得到如下方程組：

3 隱式時間離散

對式（4）和式（5）進行數值積分之后，得到的方程組如下所示：

式中：u=[u1,u2,···,uk,···,uNele]T為全局自由度矢量，Nele為全局單元的總數，uk為單元k的自由度；R(u)=[R1,R2,···,Rk,···,RNele]T為全局殘值矢量，Rk為單元k的殘值矢量；M為全局塊質量矩陣。

采用隱式時間離散方法，式（6）右端殘值項取新的時間步tn+1，計算得到：

采用向后差分方法處理之后，式（7）可以寫成：

由于求解的是非線性的控制方程，所以對式（8）的右端項進行線性化：

式中，(?R/?u)k為需要求解的大型線性方程組的雅克比矩陣。在每個時間步tn+1內采用牛頓迭代法進行求解，對于定常算例，只需進行一個牛頓步就可以達到需要的精度：

其中：k=(0,1,···,kmax)；c∈[0,1]為阻尼因子。在一個時間步內即一個牛頓迭代循環內，以第tn步的數值解作為初始值進行牛頓迭代，直到式（11）中的殘值下降到設定閾值，將第kmax個牛頓步的結果作為新的時間步tn+1的數值解并進入下一個時間步進行計算。

4 浸沒邊界法

IBM 的基本思想是通過適當的數值處理向非貼體網格施加邊界條件。體積懲罰是一種典型的方法，它通過懲罰固體中積分點的速度來施加邊界條件。

4.1 體積懲罰法

體積懲罰法通過在控制方程中引入懲罰源項來施加邊界條件。在這種方法中，首先定義一個用于區分流體區域和固體區域的界面函數：

該界面函數用于確定是否對當前積分點施加IBM力。對于移動的邊界，χ(x,t)是隨時間而變化的。對于高階笛卡爾網格的體積懲罰方法（圖1），所有被固體區域覆蓋的積分點都需要進行懲罰以施加邊界條件。

用IBM 處理的N-S 方程可以寫成：

式中，“S”為IBM 源項。

考慮固體內部速度us=(us,vs)T狄利克雷邊界條件，源項為：

式中，η為體積懲罰參數。考慮無滑移邊界條件時，設條件us=(0,0)T。本文懲罰項遵循文獻[25]中的公式，以施加絕熱壁的邊界條件。上述方程也可用于運動物體，其中固體速度根據運動方程進行更新。

通過結合算子分裂和隱式時間離散方法，控制方程等式（14）在時間上進行。使用2 階Strang 分裂[26]方法添加源項，正如Piquet 等[27]所討論的，通過Strang分裂可以精確計算動量和能量方程的懲罰項。在時間步驟n，執行以下操作：

在數值計算中，將控制方程的變量進行無量綱化處理[17]。下文中如無特別說明，懲罰參數均為η=1 × 10-3。在時間步驟n，執行第2 步，即對式（17）進行牛頓法迭代時，式（11）中的 無量綱時間步長 Δt=0.1。

4.2 邊界表示和界面函數

固體邊界的表示是IBM 方法的關鍵之一，其主要用來進行界面函數的定義和氣動系數的計算。

浸沒邊界的離散化應足夠靈活，以處理復雜的幾何形狀。在本文中，選擇使用一組拉格朗日標記點來表示實體邊界，定義為浸沒邊界點。標記點由線性元素（即二維線段）連接。使用該表示法可以有效地計算幾何量，包括曲面法線、用于數據重建的插值模板、曲面距離[28-29]。浸沒邊界由離散的點定義，點在網格中的位置用水平集方法可描述為滿足 φ=0，φ是到浸沒邊界的有符號距離[30]。

對于圓柱體、球體或機翼等簡單幾何體，存在解析形狀函數，可用于定義界面函數。例如，對于直徑為1 的圓，有：

4.3 曲面數據重建

為了從模擬結果中獲得相關物理量（如壓力、摩擦力）的分布，固體表面物理量的重建是一個重要工作。

在高階框架中，可以直接考慮使用每個單元中定義的高階多項式來執行數據重建。然而，這種方法有一些潛在的缺點，可能導致結果不準確。這主要是因為在大多數情況下，此類插值方法將涉及浸入固體中的積分點，而這些積分點通常具有非物理值。

除多項式插值外，另一種方法是從幾個最近的積分點插值數據。與基于高階多項式的插值相比，其具有更大的靈活性來選擇插值點（interpolation point,IP），而不涉及具有非物理值的固體點。這里，采用文獻[31]中描述的適用于高階框架的插值方法。通常，文獻[31]中的插值方法基于IB 點與插值點之間的逆距離。首先從IB 點周圍最近的流體點中選擇候選插值點，然后插值保守變量的值和梯度。本文采用插值點處的逆距離權重（inverse distance weight at interpolation point,IDW-IP）方法進行插值，如圖2 所示。

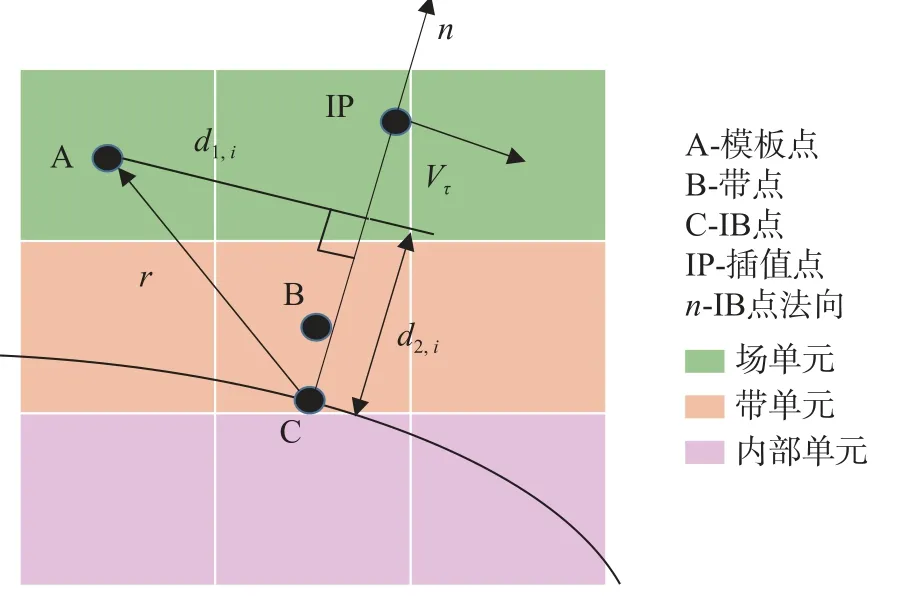
圖2 IDW-IP 方法的插值模板示意圖Fig.2 Interpolation stencil for IDW-IP method

插值點在這種情況下被定義為一個點，位于IB 點的法線上，在這個點上，屬性從周圍的單元內插，然后轉移到IB 點。關于插值點，首先要確定它的位置，其次是它的屬性。為了確定插值點的位置，使用如下關系式：

式中：d1為 A 點到IB 點法線的垂直距離；d2為A 點到IB 點的法線的距離投影；i為模板中場單元和帶單元的固體外積分點。為了確定插值點的壓力值，使用以下關系式：

在這種方法中，在插值點確定的壓力被復制到IB 點。

5 算例測試

在本節中，應用不同測試算例驗證所提出的基于高階間斷伽遼金數值方法的浸沒邊界法。

5.1 定常圓柱繞流

第一個測試案例為二維定常圓柱繞流，雷諾數和馬赫數分別設置為40 和0.2。壁面采用無滑移絕熱壁面邊界條件，因此在固體中施加us=(0,0)T。矩形計算域的大小為x∈[-5D,10D]、y∈[-5D,5D]，其 中D是圓柱的直徑，設置為1。在正方形區域x∈[-D,D]、y∈[-D,D]，使用均勻網格。均勻網格尺寸h分別選擇為0.03D（網格1）、0.05D（網格2）和0.1D（網格3）。網格1 如圖3 所示，局部均勻網格大小h=0.03D。

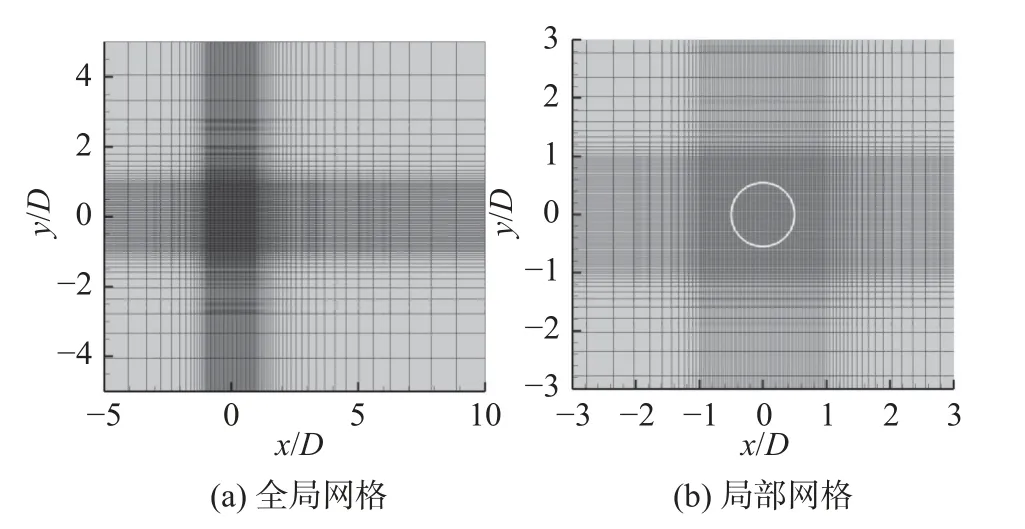
圖3 計算網格（網格1）Fig.3 Computational grid (grid 1)

在網格1 情況下，由0 階至3 階DG 計算得到的流線如圖4、物面附近馬赫數云圖如圖5所示。從圖中可以看出，隨著階數的提高，同一網格下計算結果的精度顯著提高，尤其是物面附近的數值解更加光滑。在網格1 情況下，不同階數計算得到的壓力系數Cp與文獻[11]中貼體網格模擬結果的對比如圖6 所示，圖中實線表示文獻[11]貼體網格的計算結果，符號表示本文方法數值模擬得到的結果（不同符號代表不同的階數）。結果表明，壓力系數分布隨著計算階數的提高與貼體網格結果具有良好的一致性。

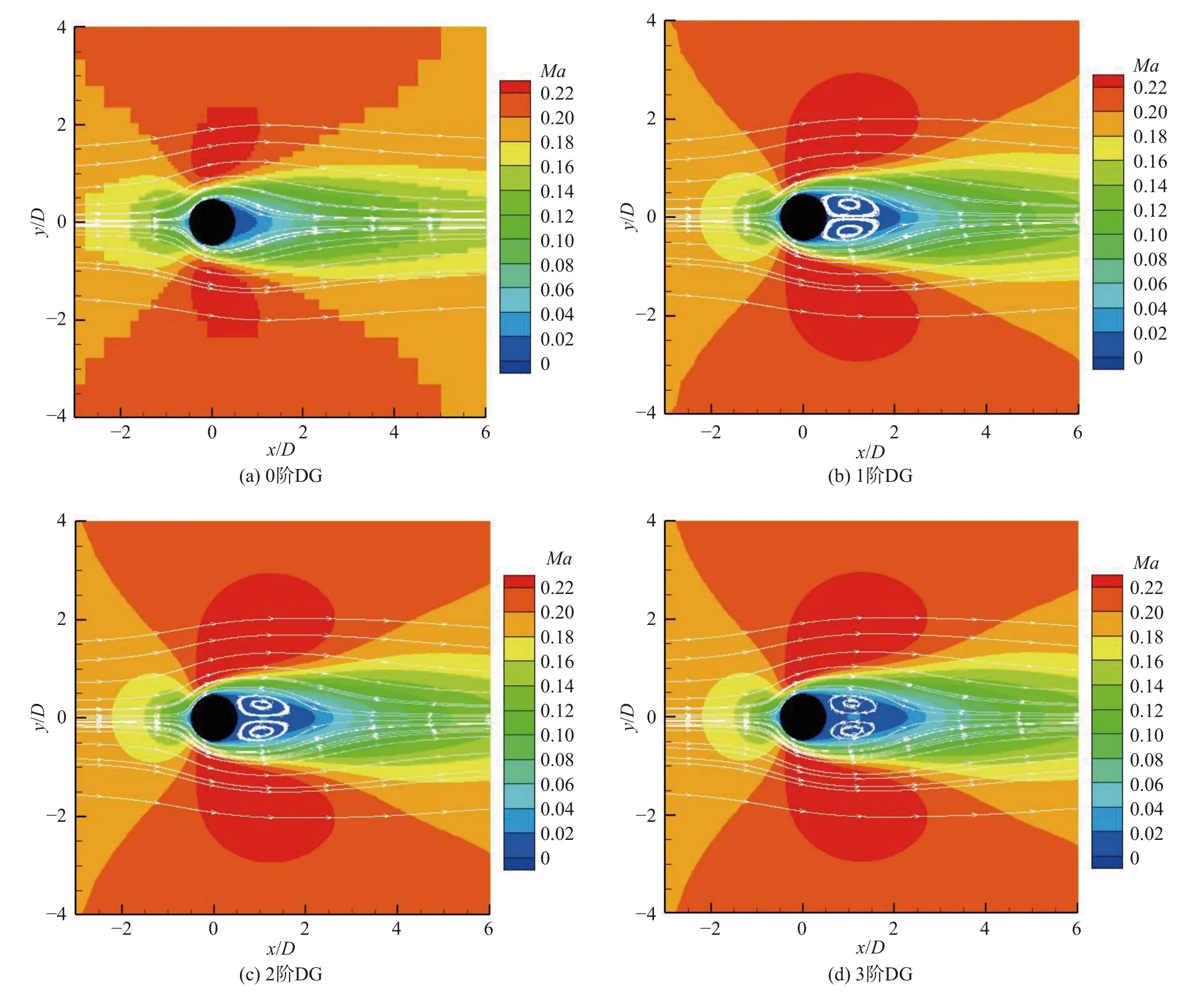
圖4 網格1 下不同階數流線圖和馬赫數云圖Fig.4 Streamlines and Mach number contours calculated by DG with different orders (grid 1)

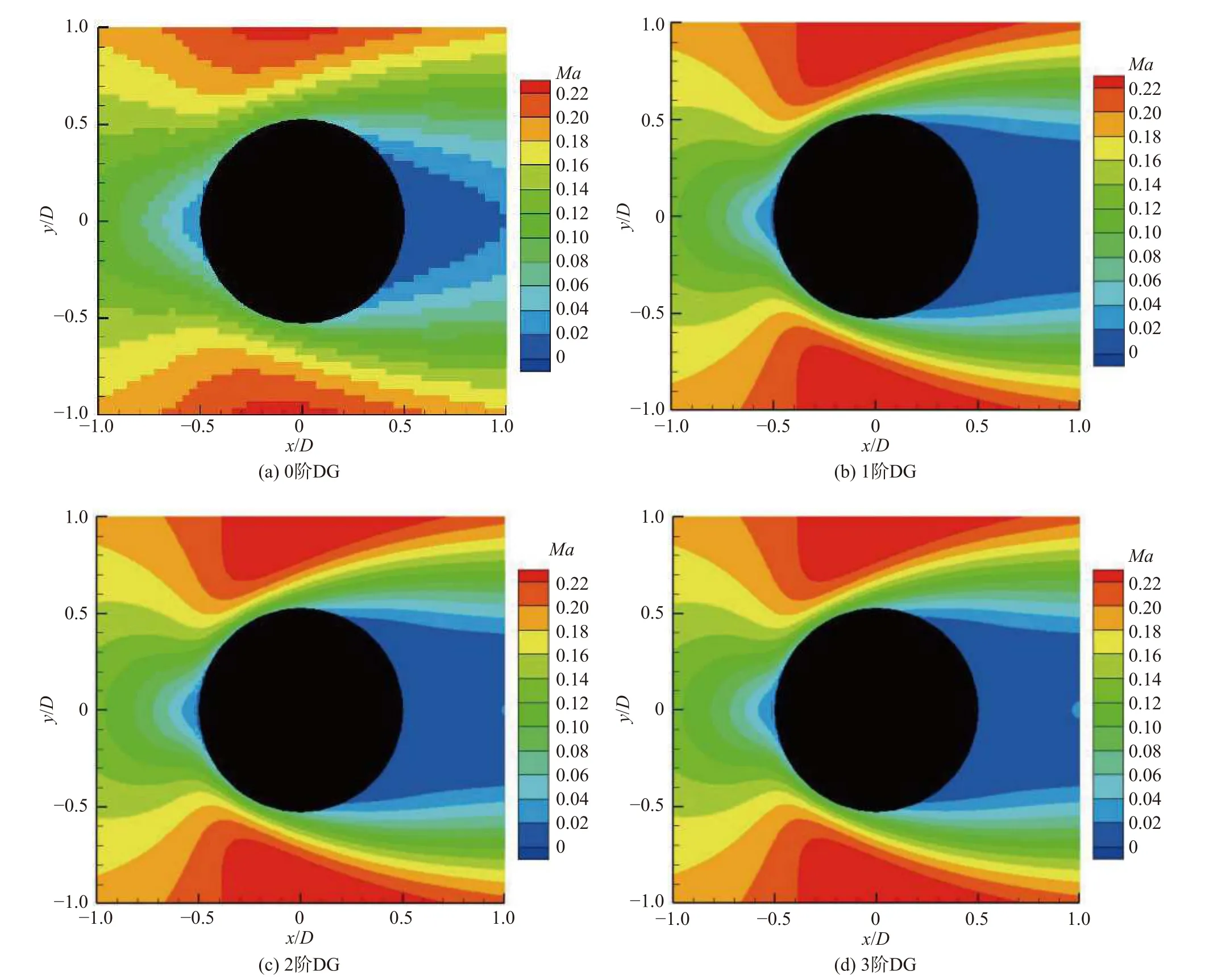
圖5 網格1 情況下不同階數物面附近馬赫云圖Fig.5 Mach number contours calculated by DG with different orders (grid 1)

不同網格尺度下壓力系數Cp的 對比如圖7 所示，圖中分別給出了0 階至3 階DG、物面附近網格尺度為0.03D、0.05D、0.1D時的結果對比。由圖7（a-d）所示，在同1 階數下，隨著網格尺度的減小Cp曲線更光滑，且總體曲線更接近文獻[11]貼體網格的測試結果；無論網格2 還是網格3，再次驗證了同一網格下，計算階數越高時精度越高，模擬計算得到的結果與文獻結果吻合越好。

設置無量綱時間步長 Δt=1 × 10-3。在網格1 情況下，1 階DG 至3 階DG 計算得到的壓力系數Cp與文獻[11]中貼體網格模擬結果的對比見圖8。結果表明，本文方法計算所得壓力系數結果與文獻結果具有良好的一致性，且階數越高與文獻結果的吻合度越高。由圖6 和圖8 可以看出，同為網格1 且懲罰參數相同時，時間步長的取值會對計算結果產生影響。與無量綱時間步長為0.1 時相比，當無量綱時間步長設置為與懲罰參數相同時（即1 × 10-3）），1 階DG 至3 階DG 得到的計算結果均更光滑且與文獻結果吻合更好。

本文方法懲罰項的添加基于Brinkman 懲罰法[25]，該方法中將固體視為滲透率極低的多孔介質。Engels等[32]研究發現，當使用顯式時間離散時，懲罰參數的選擇受CFL 的限制，顯式時間步長 Δt必須小于懲罰參數η；當采用隱式時間離散時，允許懲罰參數 η小于時間步長 Δt。Labert[33]對N-S 方程進行了研究，揭示了懲罰參數與時間步長之間的密切耦合—誤差在懲罰參數 η約等于時間步長 Δt時達到飽和。因此在體積懲罰法中通常建議 η=Δt，一種解釋為：懲罰項作為速度上的強阻尼，其引入了一個特征時間尺度，該特征時間尺度階數為η，必須用時間推進來解決。

5.2 非定常圓柱繞流

為了驗證對非定常解的有效性，測試二維圓柱周圍的低雷諾數渦脫落。當Ma=0.2、Re=200時，計算域大小為x∈[-5D,10D]、y∈[-5D,5D]，其中D是圓柱的直徑，設置為1。在正方形區域x∈[-D,D]、y∈[-D,D]，使用均勻網格，均勻網格尺寸h選為0.05D（圖9）。

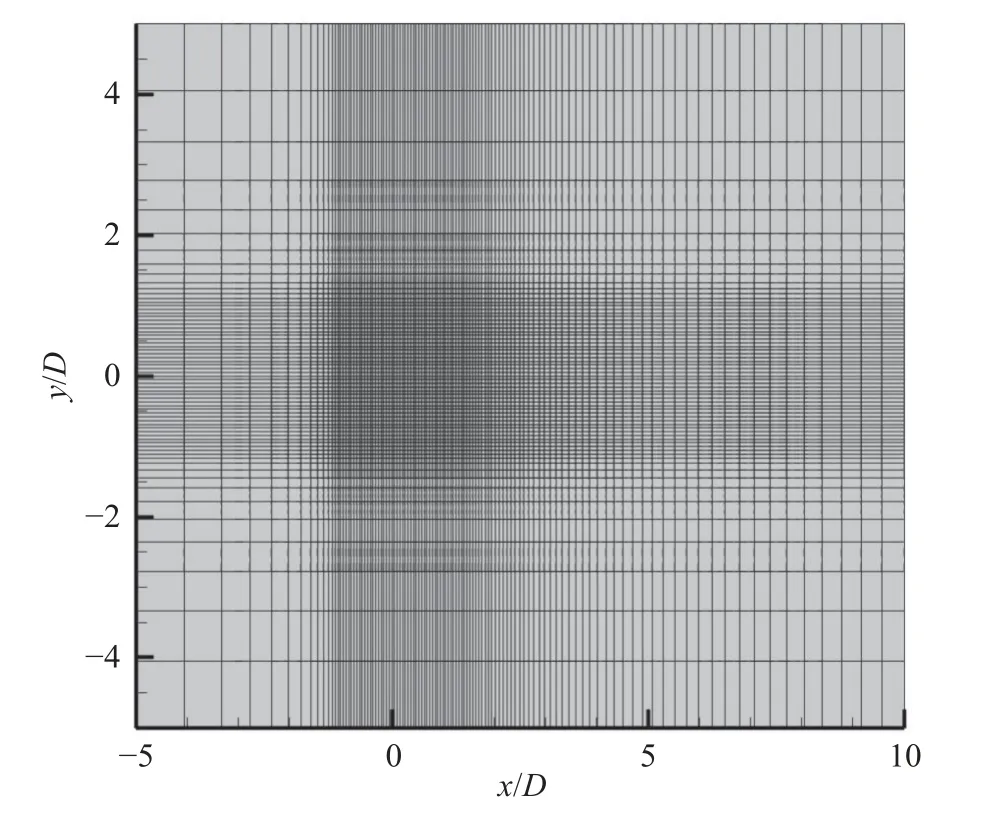
圖9 0.05D 非定常計算網格Fig.9 Computational grid for unsteady flow simulation(h=0.05D)

對不同階數下的圓柱繞流進行數值模擬，1 階DG 和3 階DG 的馬赫數云圖分別如圖10 和圖11 所示。不論1 階DG 還是3 階DG 結果，從全流場的圖上均可以看到圓柱尾跡中有周期性的旋渦脫落。從物面附近流場圖可以看出，1 階DG 的物面附近存在階梯狀，3 階DG 的物面附近較1 階DG 的更為光滑。計算描述渦脫落的特征參數St，并與文獻[34-35]對比。1 階DG 的St=0.193，3 階DG 的St=0.20，與文獻[34]中St=0.194 以及文獻[35]中St=0.194較為吻合。本文所采用的體積懲罰法對邊界條件的實現是間接的，采用的是一種弱約束方式，該方法對邊界條件的實現精度與貼體網格相比較低，邊界附近的計算精度依賴于網格密度、數值方法的精度以及懲罰參數η的設置[32-33]。

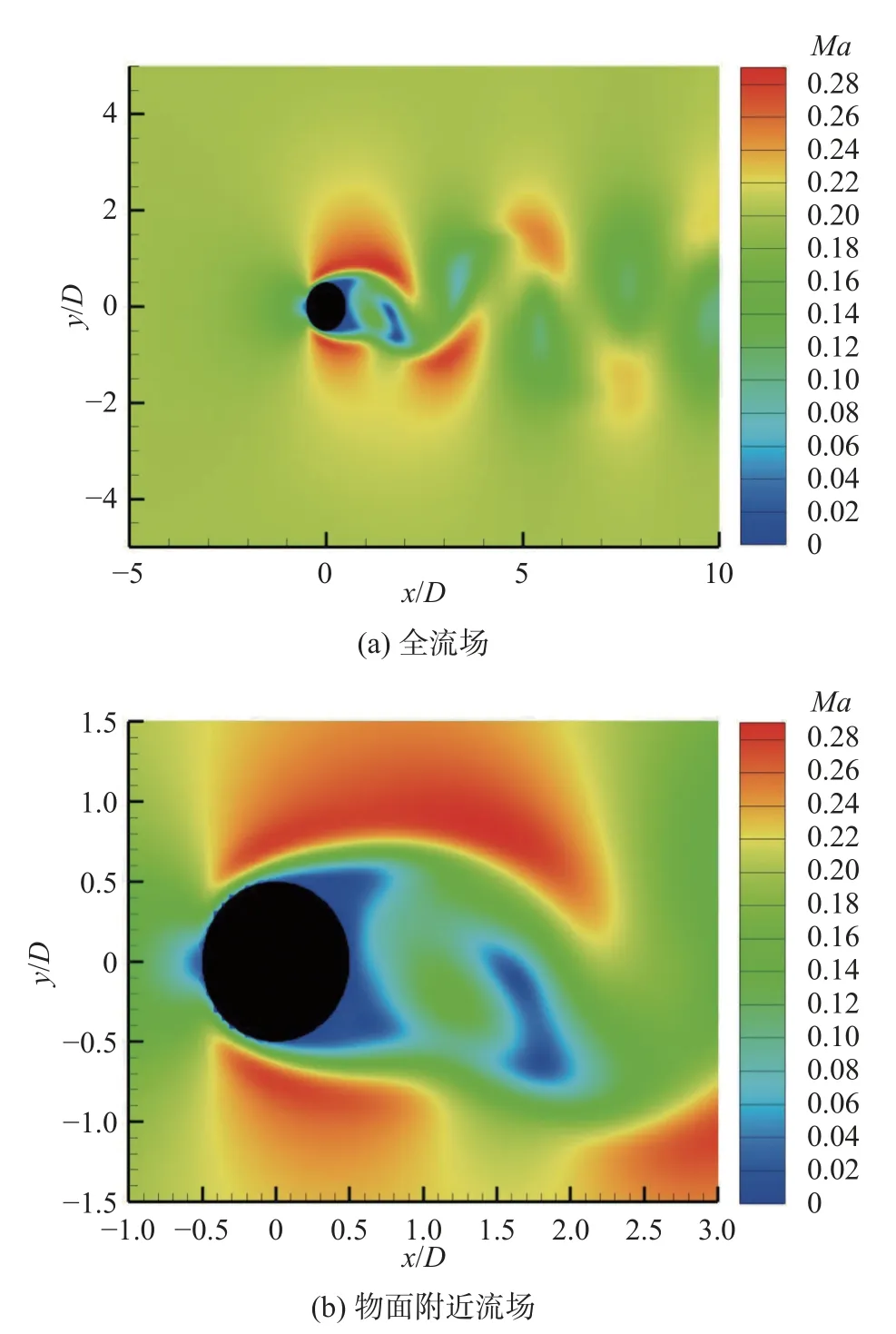
圖10 Re = 200 時圓柱馬赫數云圖（p1）Fig.10 Mach number contours at Re=200 (p1)

圖12 為中軸線y=0上時均流向速度分布。由圖可看出，1 階DG 和3 階DG 的模擬結果中，圓柱內部的速度為0，同時沿來流方向在圓柱后方近壁面流速為負值，存在先減后增的趨勢，故圓柱后方存在回流區，在遠處流速趨于穩定。整個回流區及近尾區的流速分布與文獻[34]結果吻合良好，但在恢復遠區，可能由于遠處網格尺度較大導致本文計算的結果偏小。總體上，3 階DG 的結果相較于1 階DG 更接近文獻[34]的結果。

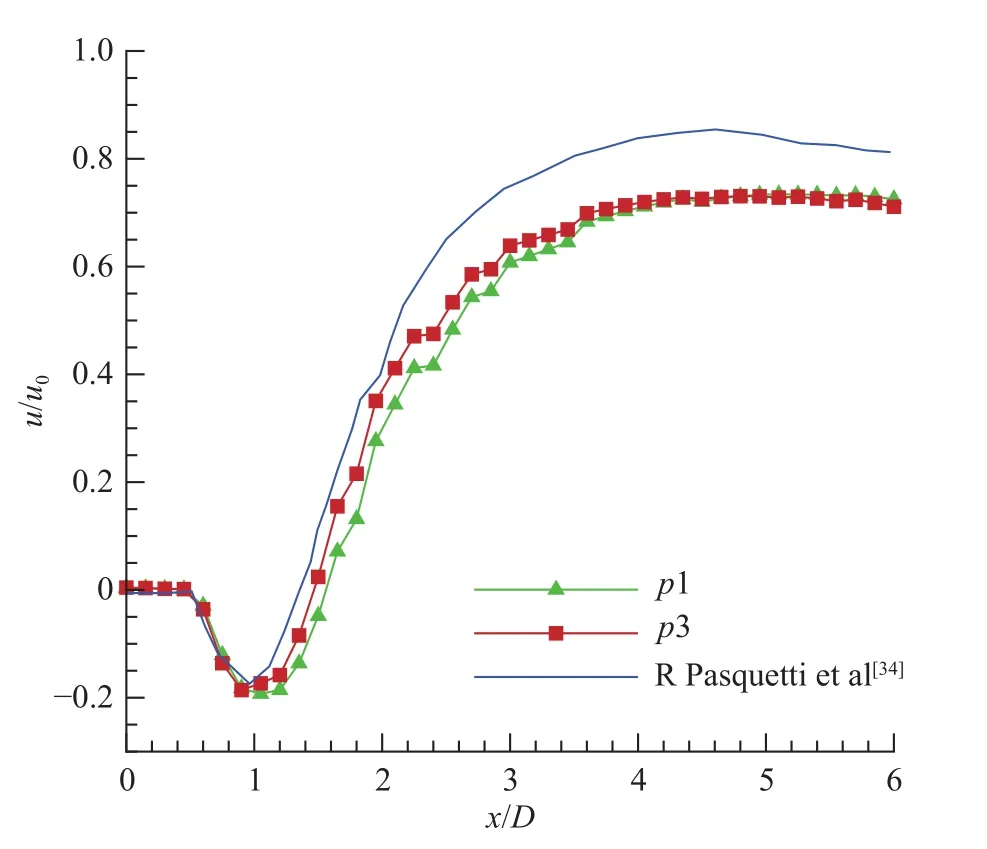
圖12 沿中軸線y=0的時均流向速度分布Fig.12 Mean streamwise velocity in the y=0 direction

圖13 至圖15 分別給出了圓柱后的三個不同剖面x/D=1.0、2.0、4.5 上的時均流向速度分布。圖中實線為文獻[34]計算結果，實心三角和空心方形分別表示1 階DG 和3 階DG 的計算結果。可以看出，1 階DG 和3 階DG 的計算結果與文獻[34]結果在不同剖面處流向速度隨坐標的變化規律一致，均關于圓柱中心線（y/D=0）對稱，且在兩側趨于穩定數值。通過三個剖面處的結果對比，可以看出，同一網格下3 階DG 的計算結果相較于1 階DG 的計算結果與文獻更為吻合。總體來說，本文方法成功模擬了低雷諾數下非定常問題，且階數越高模擬的結果精度越高。

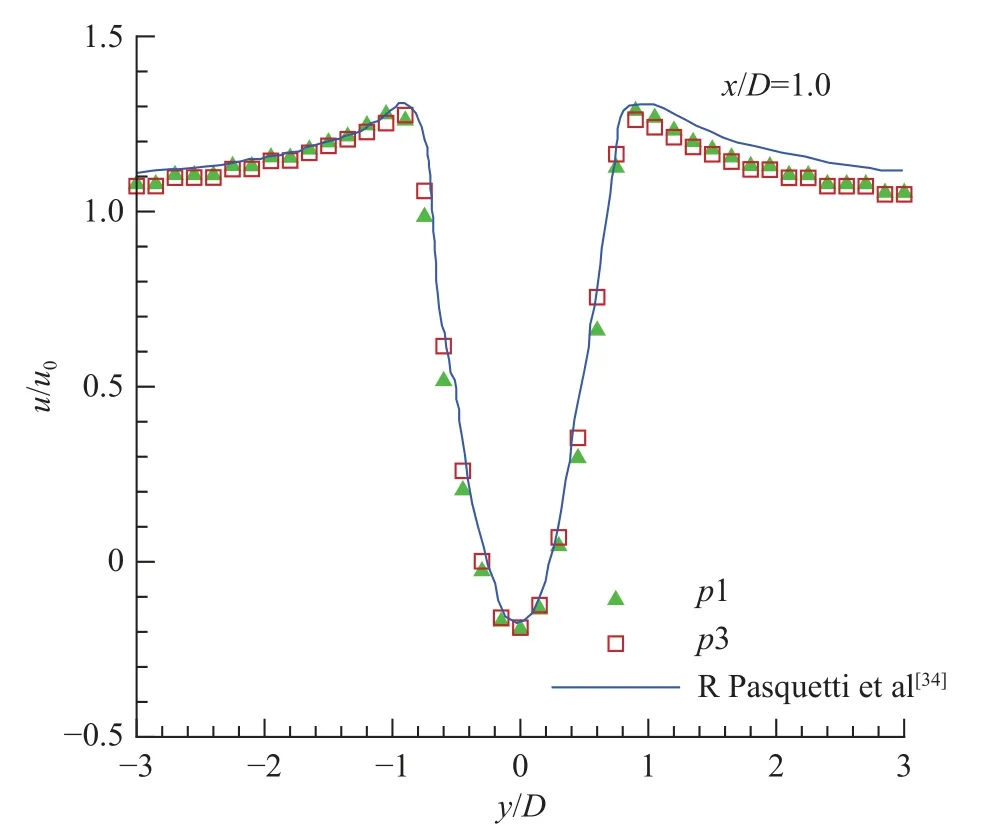
圖13 x/D=1.0截面的時均流速分布Fig.13 Mean streamwise velocity atx/D=1.0

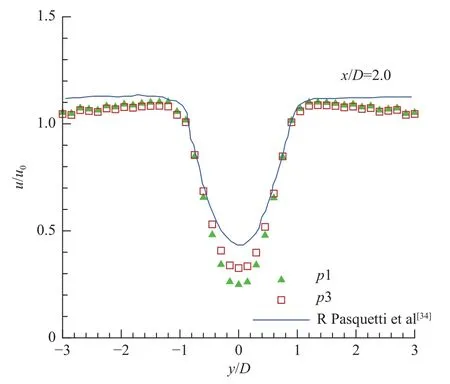
圖14 x/D=2.0截面的時均流速分布Fig.14 Mean streamwise velocity atx/D=2.0

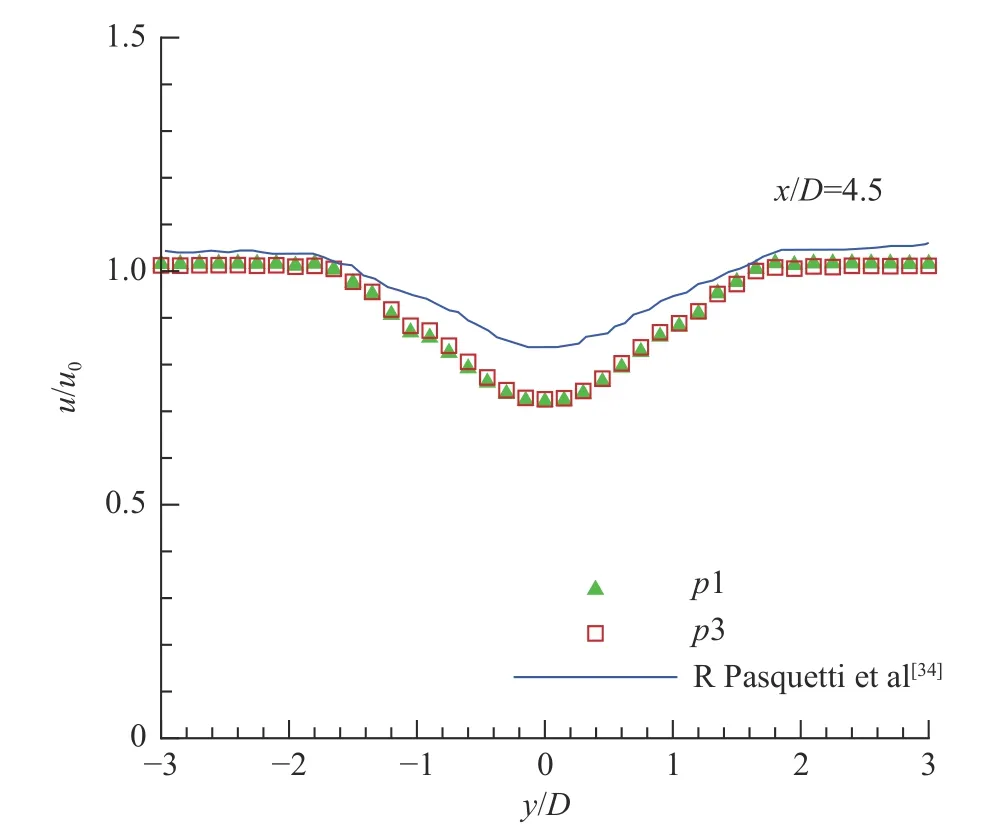
圖15 x/D=4.5截面的時均流速分布Fig.15 Mean streamwise velocity atx/D=4.5

6 結論

本文提出了適用于可壓縮流動數值模擬的結合高階DG 的浸沒邊界法，用體積懲罰方法來實現物面邊界條件，避免了切割網格。相較于顯式迭代，對懲罰項采用隱式時間離散允許較小的懲罰參數。采用IDW-IP 方法對物面附近的數據進行重建，以獲得物面表面壓力。研究得出以下結論：

1）通過不同的流動模擬，包括靜態圓柱定常和非定常的流動，驗證了本文方法計算可壓縮流動的有效性和準確性。

2）高階DG 的高精度優勢在本文的浸沒邊界方法中得到了顯著體現。隨著計算階數的提高，邊界條件的實現精度以及整體的數值精度都得到了顯著提高。

3）與貼體網格方法相比，IBM 最大的優勢在于網格生成十分簡單，缺點在于邊界條件的實現是采用弱約束方式，因此邊界處理的精度不如貼體網格方法，計算結果依賴于網格密度、高階DG 的階數以及懲罰參數 η的設置。

4）本文方法為未來復雜外形及移動邊界等要求高質量貼體網格的計算提供了更為簡便的思路。但對移動邊界的處理還需進一步研究驗證。