基于阻抗分離的工業諧波源非侵入式識別方法

齊 屹，陳書暢，林才華，張 逸

（1.國網寧夏電力有限公司經濟技術研究院，銀川 750004；2.福州大學電氣工程與自動化學院，福州 350108；3.國網福建電力有限公司電力科學研究院，福州 350108）

隨著工業化進程的不斷加快，具有非線性和沖擊性工業負荷的投運規模顯著增加[1-3]。電弧爐、感應加熱爐和大型整流器等工業負荷會產生大量諧波，使電網的諧波污染日益嚴重，影響電網的安全穩定運行[4-6]。工業用戶的非線性設備是電網中主要的諧波源負荷之一，對其進行檢測識別，不僅有助于提高電網公司的電能質量管控水平，還能為用戶的用電服務需求分析和電能質量治理方案的制定提供重要的技術支撐[7]。

傳統的諧波源辨識方法主要分為基于等效電路的諧波源辨識和基于諧波狀態估計的諧波源辨識[8-9]。前者通常以戴維南等效電路模型或諾頓等效電路模型為基礎，原理較為簡單直觀，其包括功率方向法、臨界阻抗法、波動量法等，但該類方法一般僅能判斷諧波源是位于系統側還是用戶側[8，10-11]；后者在諧波源信息未知的情況下，利用有限節點的監測數據即可追溯整個系統的諧波源情況，目前得到廣泛的應用。文獻[11-13]采用盲源分離法估算諧波源與各節點間的諧波阻抗以定位全網諧波源；文獻[14]通過分形分析非線性負荷的諧波特性，實現諧波源特征提取與檢測；文獻[15-17]采用數據分析技術對多個節點的采樣數據進行特性分析以實現諧波源定位；文獻[18]利用諧波源與非諧波源的負荷阻抗參數特性差異識別并定位諧波源，但該方法需要各負荷供電線路的電能質量監測數據，在實際應用中較難獲取；文獻[19]基于SOM 神經網絡實現諧波源的檢測與定位，但需要各類型諧波源單獨運行時的負荷阻抗參數特性作為訓練樣本，實際應用時難以獲取。上述方法雖能實現全網諧波源的檢測識別，但僅能判斷出母線下是否存在諧波源，無法對具體諧波源負荷類型進行識別，且還需要足夠的冗余測量，計算量較大，工程應用較難。

非侵入式負荷識別作為新一代智能電網發展的重要技術之一，其僅對某一特定區域的總負荷電表數據進行分析處理，即可辨識該區域內各用電負荷的相關情況，目前主要用于家電負荷[20-21]。文獻[22-23]通過對電壓、電流等負荷特征進行顏色編碼，構建負荷標識模型，有效提高了辨識正確率，但需預先構建負荷特征庫；文獻[24]采用深度學習框架，提出一種基于seq2seq 和Attention 機制的非侵入式負荷分解模型，但需大量的訓練樣本且特征庫的普適性較差。針對這一問題，文獻[25]提出一種自適應特征庫構建方法，提高非侵入式負荷監測的普適性和準確性，但需依賴于負荷的啟停狀態，適用范圍較窄；文獻[26]考慮負荷運行模式提出一種新穎的非侵入式負荷模型，提高負荷主動識別和預測的性能。近年來，除家電負荷外，非侵入式負荷監測在能源、航空等領域也得到了廣泛的應用[27-28]。上述非侵入式研究主要依托負荷特征庫的構建，但無論是預先建立特征庫，還是實時構建自適應特征庫，要么要求負荷存在易于檢測單獨運行特性，要么要求負荷存在易于檢測的啟、停狀態等暫態過程。現有工業負荷非侵入式識別大多以上述思路為基礎[29-30]，但對于工業負荷，由于其用電連續性和生產工藝完整性的要求，對短時的獨立運行特性、易于檢測的啟停狀態和暫態過程的獲取較為困難。因此，傳統的非侵入式負荷監測方法難以直接應用于工業負荷。

針對上述問題，本文提出一種適用于工業用戶諧波源負荷的非侵入式識別方法。首先，基于負荷等值阻抗時域模型，構建多負荷網絡等值阻抗關聯模型；然后，以關聯模型為基礎，采用改進型的復局部均值分解CLMD（complex local mean decomposition）和復值快速獨立分量分析FastICA（fast independent component analysis）對綜合等值阻抗信號進行分離，實現各支路等值阻抗信號的非侵入式分解；最后，分別采用Maltab/Simulink 仿真和某變電站實測的三相電壓、電流數據來驗證方法的有效性和適應性。

1 工業用戶諧波源負荷檢測原理

現代非線性工業負載設備主要分為電弧型設備和電力電子開關型設備兩類[5]。電弧型設備一般包括電弧爐和電焊機等，而電力電子開關型設備一般為感應加熱爐、變頻器和整流器等。這兩類非線性設備的特性不同，所產生電能質量問題的特點也不同，需要定制不同的電能質量治理方案，例如：電弧爐通常用靜止無功補償裝置和無源濾波器聯合治理；電力電子型設備常用有源濾波裝置進行治理[38-39]。若能識別這兩類非線性設備，則能對電能質量治理工作提供支撐，因此，本文研究主要面向識別電弧型負荷和整流型負荷這兩類典型諧波源。

上述兩類典型諧波源可以用RL模型進行等效，其參數R和L是一個隨時間變化的函數，且不同類型諧波源的阻抗特性明顯不同，而同類型諧波源通常呈現相似的阻抗特性[7，18]。因此，本文采用電阻、電感串聯的等效阻抗來表示負荷模型，從負荷等值阻抗入手，構建多負荷并聯網絡中綜合等值阻抗與各支路等值阻抗間的關聯性模型，為工業用戶諧波源非侵入式負荷識別方法的研究提供理論和技術支撐。

1.1 諧波源負荷等值阻感模型

用電阻和電感串聯的等效阻感來表示的負荷模型如圖1所示。圖1 中，s為系統等值電源；Zs為系統等值阻抗；u(t)、i(t)分別為采樣點測得的電壓和電流瞬時值；R、L分別為負荷等值阻感參數中的電阻參數和電感參數，均隨時間變化。

圖1 負荷等值時域電路模型Fig.1 Load equivalent circuit model in time domain

由圖1 可得，采樣點處電壓、電流與負荷等值阻感間的關系為

式中：uL(ξ)為ξ時刻的等效電感電壓；t0為起始時刻；t為結束時刻。

參照微元法的思想，將時變的負荷等值阻抗參數進行分段線性化計算。由于負荷等值阻抗參數的變化頻率遠小于采樣頻率，所以在一個微元時間內，認為R、L值可在至少連續相鄰的4 個采樣點上保持不變，根據梯形等效法，設4 個采樣時刻分別為t1、t2、t3、t4，Δt=t3-t1，則有[19]

其矩陣形式可表示為

1.2 多負荷網絡等值阻抗并聯模型

工業負荷間大多呈現并聯關系，結合第1.1 節所述的等值阻抗，本文將多負荷系統等效為多阻抗并聯電路如圖2所示。圖2 中，Rk、Lk分別為第k個支路的負荷等值電阻和等值電感；ik為流過第k個支路的電流；n為并聯總支路數。

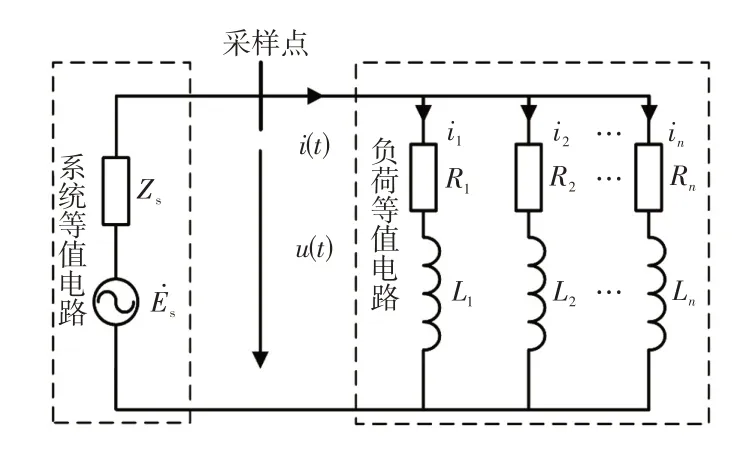
圖2 多負荷并聯等值電路模型Fig.2 Multi-load parallel equivalent circuit model

根據并聯網絡的電路特性建立電壓、電流及阻抗的關系式，即

由阻抗并聯計算公式可得

將式（5）～（7）進行整理簡化，構建綜合等值阻抗與各支路阻抗間的關系式，即

式（8）中的綜合等值阻抗參數R和X可由式（3）求得，即，等號左側的綜合阻抗信號可認為是已知的，而等號右側的各支路阻抗信號和比例系數則均是未知的。因此，可考慮采用盲源分離算法來實現式（8）支路阻抗信號的分離。

2 基于改進型CLMD 的單通道盲源分離

盲源分離指的是從觀測到的混合信號中分析出沒有觀測的原始信號。但該類算法通常要求能檢測到的混合信號個數不少于待估計的源信號個數，即，僅利用式（8）左側所示的單通道阻抗數據，無法實現各支路阻抗數據的分離[31-34]。因此，本文在采用盲源分離算法來實現支路阻抗信號的分離前，需先構建虛擬輸入通道，以滿足算法的應用要求。

2.1 基于改進型CLMD 的虛擬通道構建

目前，用于構建虛擬通道以解決欠定問題來滿足盲源分離算法應用要求的方法主要有局部均值分解LMD（local mean decomposition）、經驗模式分解EMD（empirical mode decomposition）和奇異均值分解SVD（singular value decomposition）[33-34]。其中，SVD需根據待分離信號來構建并求解軌道矩陣，才能構建虛擬通道信號，計算量較大、求解速度較慢、效率較低，且占用的內存較大，難以實際應用；EMD與LMD 類似，但EMD 分解數量多、迭代次數多、精度較差；由于EMD方法使用了希爾伯特變換，導致原始信號的振幅和頻率信息有所缺失，造成EMD結果不穩定、不準確。本文考慮阻抗信號的復數形式，選取CLMD 算法來構建虛擬通道，以滿足復值FastICA的應用需求。

CLMD是LMD向復數域的一種擴展，其能依據信號本身的包絡特性自適應地將信號分解為若干個瞬時頻率具有實際物理意義的乘積函數PF（product function）分量之和，更準確地反映信號能量在空間各尺度上的時頻分布規律[34-36]。它通常首先將復數域的阻抗信號投影到0 和π/2 兩個方向，即將Z(t)=R(t)+jX(t)轉化為二元信號；然后，采用與LMD相似的方法分別處理各投影方向上的分量，以獲得局部均值函數和局部包絡函數，進而得到Z(t)實部和虛部的調頻FM（frequency modulated）信號和包絡信號；最后，將包絡信號和純調頻信號相乘，得到PF分量。

對于在復數域下的觀測信號，CLMD 算法有以下處理過程。

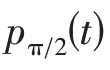
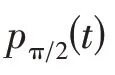
步驟3復局部均值函數。復數信號Z(t)的局部均值函數可表示為

步驟4去復局部均值函數處理。由信號Z(t)中減去局部均值函數m(N,M)(t)，即

步驟5調頻信號。由局部包絡估計函數對h(N,M)(t)進行解調，得到調頻信號s0(N,M)(t)和s(π/2)(N,M)(t)為

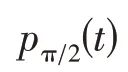
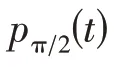
式中，l為迭代總次數。

步驟7復值PF 分量。根據不同投影方向的調頻信號和包絡信號，可得第N個PF分量為

步驟8殘留信號。將PF分量從原始信號Z(t)分離出來，可得殘留信號uN(t)為

將uN(t)作為新的Z(t)，重復步驟1～8。循環迭代的終止條件為殘留信號uN(t) 不存在旋轉模式[34-36]。

值得注意的是，滑動平均法的跨度及端點效應現象會嚴重影響CLMD算法的精度和收斂速度，而過于苛刻的迭代終止條件亦會嚴重降低算法的計算速率[36]。因此，本文結合現有研究對CLMD 算法進行改進，具體改進方案如下。

（1）采用分段三次Hermite 插值來代替滑動平均法，提高局部均值函數和包絡估計函數的計算精度。

（2）利用極值延拓法來改善CLMD 的端點效應，降低端點失真對分解結果的不良影響。

（3）包絡信號估計的迭代終止條件為包絡估計函數與1的差值向量最大奇異值小于變動量Δe；殘留信號uN(t)的迭代終止條件為信號極值點小于3或信號能量小于源信號能量的10%[36-37]。

根據上述改進型CLMD 算法的計算過程，對阻抗信號Z(t)進行分解，即可得到一系列PF分量。在此基礎上，將Z(t)與其相關性較高的PF分量進行組合，形成一個新的多通道混合信號Znew(t)，以滿足復值FastICA算法的應用要求。

2.2 盲源分離模型

圖3 盲源分離的理論模型Fig.3 Theoretical model of blind source separation

由圖3可得，線性盲源分離的信號混合模型為

由混合信號x(t)中分離出各源信號，其解混模型可表示為

目前，分離矩陣W的估算方法有很多，考慮到式（8）中的非線性負荷支路阻抗模型為復數形式，本文采用復值FastICA算法對支路阻抗信號進行分離[32]。相比于信息最大化算法、非負矩陣分解和最大似然算法，其收斂速度更快、分離效果更好、迭代更穩定，還可實現非高斯獨立分量的分離[32-34]。

復值FastICA算法通常是以“自下而上”的獨立分量分析來構造目標函數，可定義為

式中：E{}為均值運算；G（）為任意的非二次函數；w=[w1,w2,…,wm]T為m維的復值分離向量，表示分離矩陣W中的一行；（）H為矩陣轉置共軛；為對x(t)進行去均值、白化處理后的數據，其步驟如下。

步驟1去均值處理。去均值是指將所有的采樣信號減去其均值，可得一組零均值的信號，其表達式為

式中，λ為拉格朗日乘子。

以獲得目標函數的極值為目標，采用Newton法對式（21）進行優化，其中的復向量實部和虛部分開進行求導，以此化簡得到復值分離向量w的迭代公式為

式中：g()為G()的導數；g'()為g()的導數。

在對各分量進行迭代分離的過程中，要保證每一個新的分量是獨立且唯一的，因此，在新向量wk+1迭代運算前，需進行相應的去相關和歸一化處理，即

式（22）和式（23）構成了基于復值FastICA算法的盲源分離迭代分離規則。當m≥n時，為非欠定盲源分離，可由式（22）和式（23）直接實現信號分離；當m＜n時，為欠定盲源分離，在無其他限定條件下，盲源分離為非唯一解，針對該種情況，可采用第2.1節所述構建虛擬通道的方法以將欠定模型轉換為非欠定模型。

3 基于單通道盲源分離的非侵入式工業諧波源負荷識別方法

根據第1、2 節分析可將工業用戶諧波源負荷非侵入式識別算法的具體步驟總結如下：

步驟1根據工業用戶母線采集得到的電壓、電流采樣數據，通過第1.1 節所述方法計算得到負荷的綜合等值阻抗；

步驟2利用模型識別[18]的方法判斷該用戶是否為非線性用戶；

步驟3若為非線性用戶，則根據第2.1節所述的改進CLMD算法對綜合等值阻抗信號Z(t)=R(t)+jX(t)進行分解，將分解得到的乘積分量PFN與綜合等值阻抗信號Z(t)=R(t)+jX(t)進行組合，以此得到新的混合負荷阻抗信號Znew(t)；

步驟4根據第2.2節所述的復值FastICA算法對新的混合阻抗信號Znew(t)進行分解，以分離得到估計的各負荷支路阻抗信號，從而判斷識別出工業用戶所含有的諧波源負荷類型。

綜上所述，基于改進CLMD-FastICA 的非侵入式工業用戶諧波源負荷識別方法的流程如圖4所示。

4 算例分析

4.1 仿真算例分析

4.1.1 仿真算例設置

對于大型工業用戶，其供電母線一般會專門提供一條出線給同一類的大容量工業設備供電，因此本文以某工業用戶的供電系統為參考，在Simulink 仿真平臺搭建三相綜合負荷仿真模型如圖5所示。

圖5中，z1為線性負荷；z2為電弧爐短路阻抗；z3為整流設備直流側的等值阻抗；電弧爐仿真模型由文獻[40]所述方法構建。考慮到工業用戶主要包含的諧波源負荷類型及容量，仿真模型主要參數如表1所示。采樣頻率為20 kHz、時間為0.2 s。

由圖5 可知，數據監測點位于電網側10 kV 供電支路上，即未獲取用戶詳細的用電數據。以情景1 為例，監測點采集得到的三相電壓和電流數據如圖6所示。

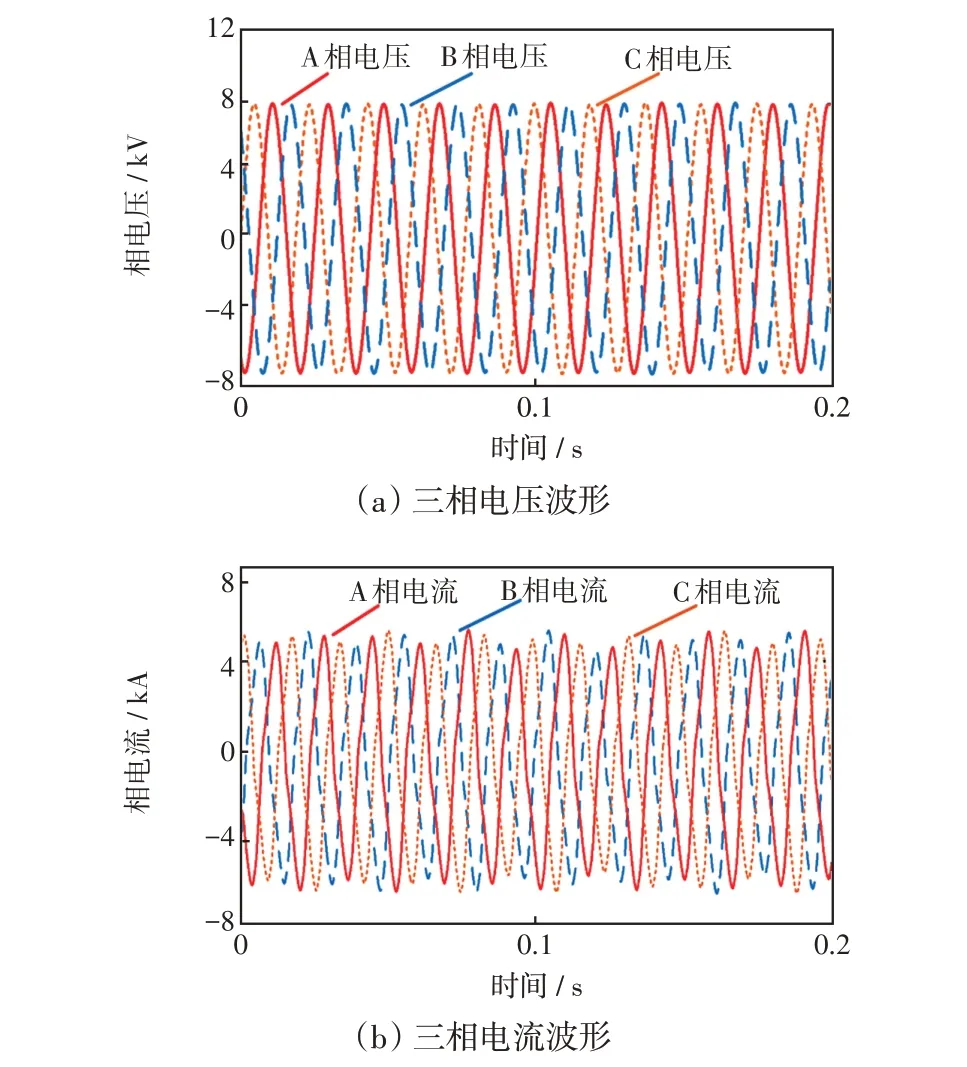
圖6 測點處的三相電壓、電流波形Fig.6 Waveforms of three-phase voltage and current at monitoring point

表2 給出了表1 所述4 種不同情景下監測點電壓、電流的各次諧波含量情況及總諧波畸變率THD（total harmonic distortion）。

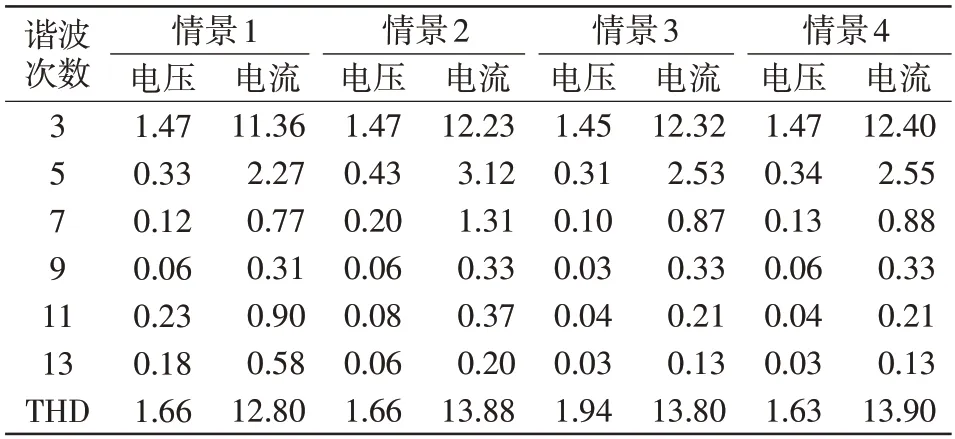
表2 監測點電壓、電流的諧波含有率Tab.2 Harmonic content of voltage and current at monitoring point%

由表2 可以看出，僅從負荷的諧波數據特性較難細致地分辨出該支路所帶的諧波源負荷類型。

4.1.2 諧波源負荷類型識別

以情景1 為例，監測點處的負荷綜合等值阻抗參數R和X隨時間變化的趨勢如圖7所示。

圖7 綜合負荷等值參數Fig.7 Equivalent parameters of integrated load

由文獻[18]的方法判斷出該用戶為非線性用戶，因此利用第2.1 節所述的改進型CLMD 算法對圖7所示的綜合等值阻抗信號Z(t)=R(t)+jX(t)進行分解，復值PFN（N=1，2，3）如圖8所示。

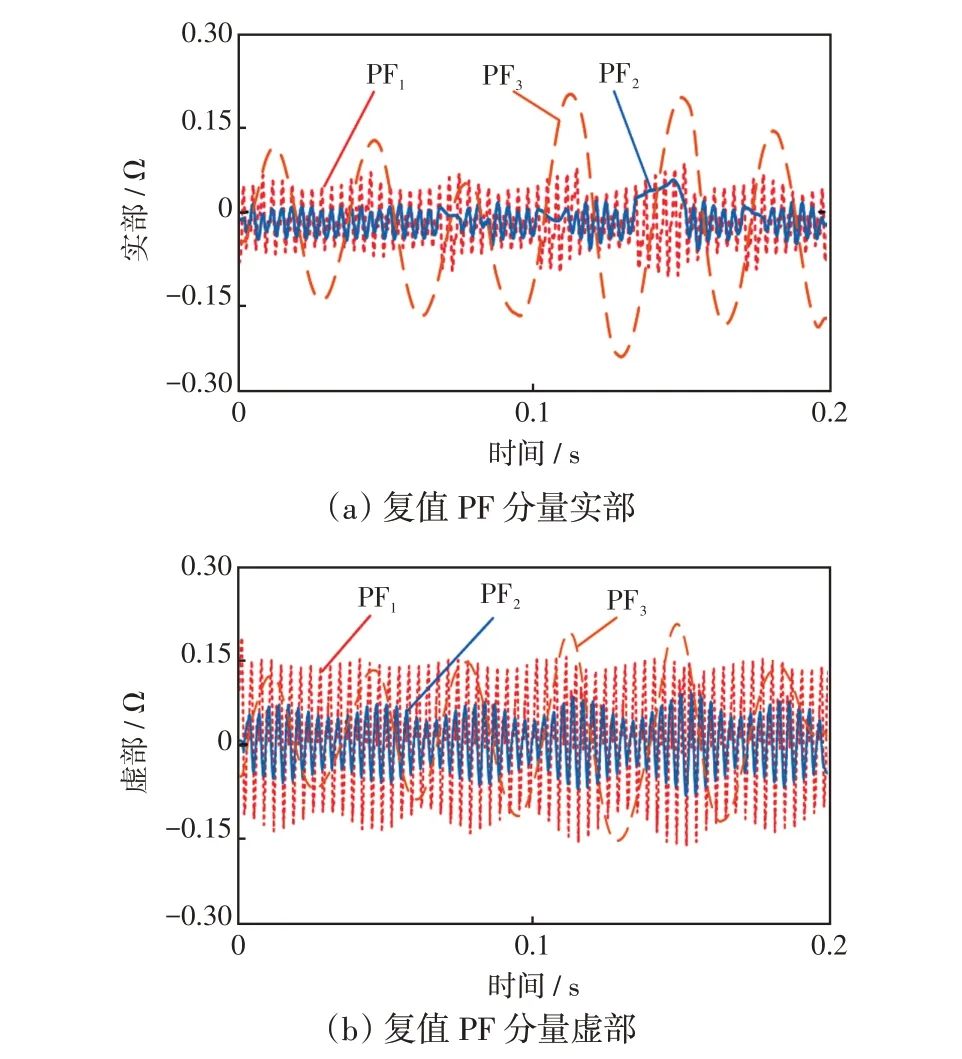
圖8 分離得到的乘積信號分量Fig.8 Separated product function components

在獲得PF 分量后，計算其與綜合等值阻抗z(t)間的相關系數，其值如表3所示。值得注意的是，整體相關系數表示兩信號間整體變化趨勢的相似程度；局部相關系數表示兩信號所含局部細節特征的相似程度。考慮到盲源分離算法的特性，本文在計算PFN（N=1，2，3）與阻抗信號間的相關系數時，還需充分考慮信號的局部特性。

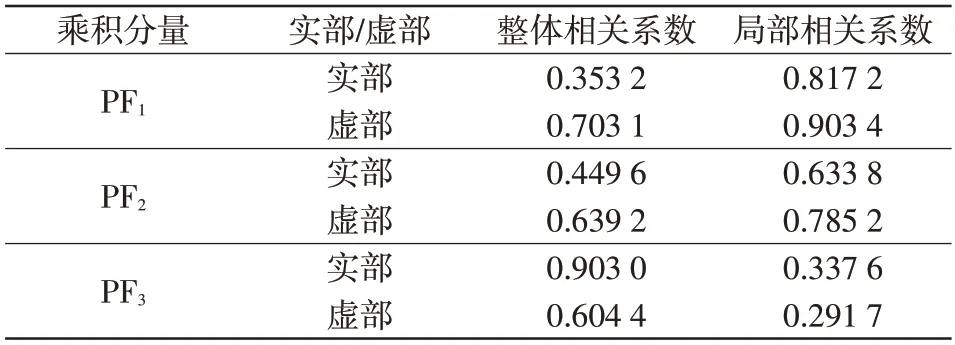
表3 改進型CLMD 分解結果的相關系數Tab.3 Correlation coefficient of decomposition results obtained by improved CLMD algorithm

選取局部相關系數最好的PF1分量與z(t)一起構成新的混合信號znew(t)。在此基礎上，采用第2.2節所述的復值FastICA 算法對新混合信號znew(t)進行分離重構，歸一化后得到的估計支路阻抗信號波形與實際波形如圖9、10所示。

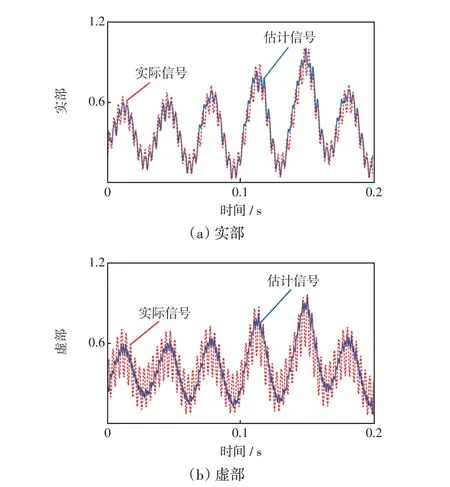
圖9 分離信號1 的估計值與實際值Fig.9 Estimated and actual values of separation signal 1

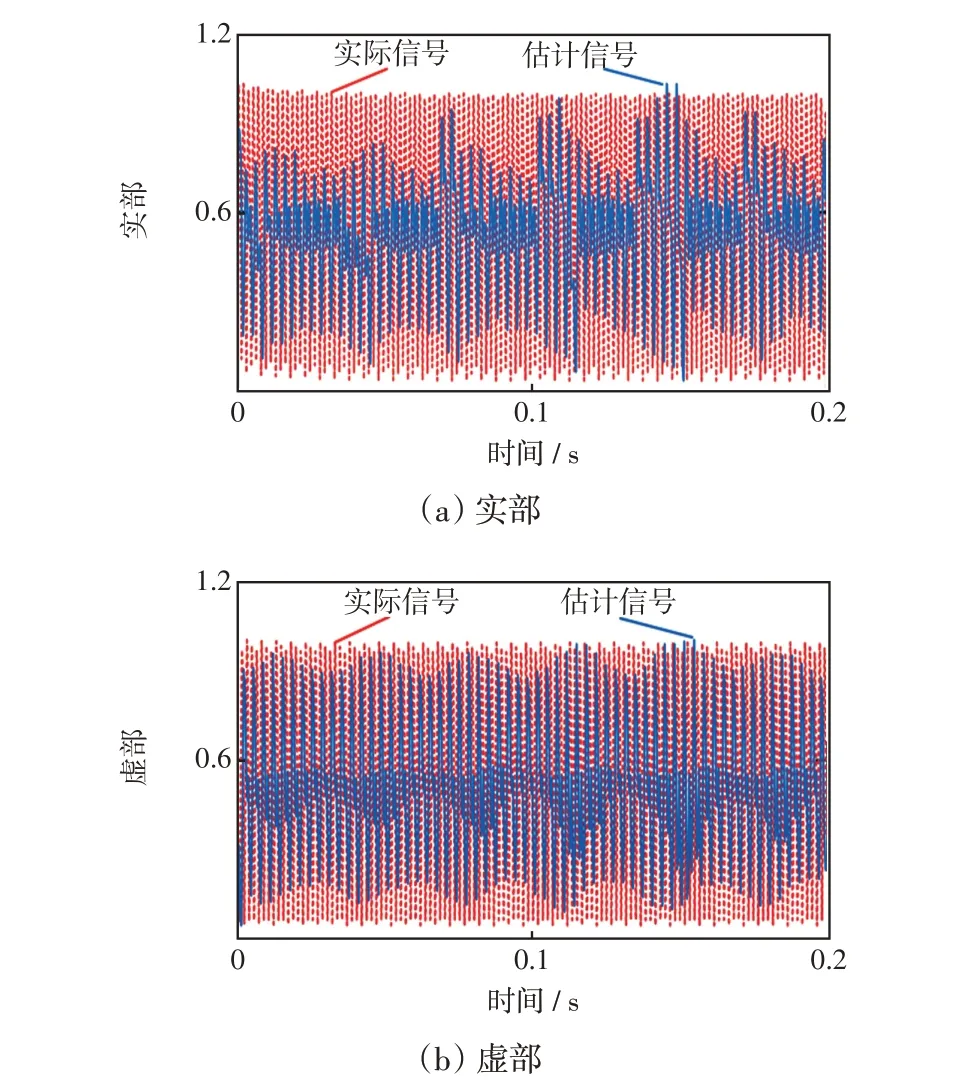
圖10 分離信號2 的阻抗實際值與估計值Fig.10 Actual and estimated load impedance of separation signal 2

由圖9、10 可以看出，本文所提出的盲源分離算法得到的支路阻抗信號波形與實際波形的吻合度較高，驗證了本文方法在阻抗信號分離重構方面的可行性。為了更好地體現結果的正確性，采用相關系數來衡量估計信號與實際信號實部和虛部的差異性，結果如表4所示。

表4 諧波源負荷阻抗估計信號與原信號的相關性Tab.4 Correlation between estimated signal of harmonic source load impedance and original signal

由表4 可知，分離信號1 估計值和實際值間的相關系數達到了0.74 以上，表明兩者具有高相關性；分離信號2估計值和實際值間的相關系數雖然僅為0.37，即中度相關性，但估計信號仍然呈現出實際信號的變化趨勢，足以用于判斷諧波源負荷的類型。相關性相對較低的情況主要是由于存在容量明顯大于其他負荷的諧波源，在一定程度上影響其他諧波源負荷阻抗幅值的估計。

由上述分析可以認為該10 kV供電支路存在兩種非線性負荷，而圖9、10 中的兩種類型諧波源的阻抗信號波形特征存在顯著差異，可通過經驗觀察或波形匹配等方法進行區分。由諧波源負荷的阻抗特性可得，分離阻抗信號1具有明顯的周期性特征，且在此基礎上帶有一定的噪聲，符合電弧的電氣特性[38]，因此是電弧型設備；分離阻抗信號2的特性較為平穩，一般是小功率感應加熱爐等整流型負荷。

與情景1 識別過程類似，對情景2、情景3 及情景4 下的電網側三相電壓和電流監測數據進行分析，判斷識別用戶的負荷類型，其識別結果如表5示。表5中，“√/√”表示該用戶存在該類型負荷且本文方法識別結果正確。

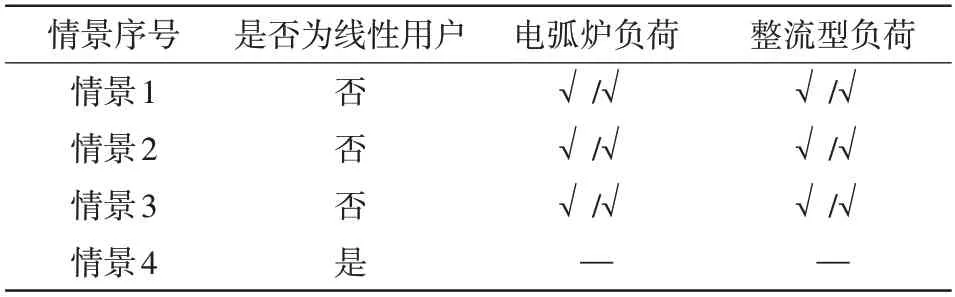
表5 各場景下的負荷識別結果Tab.5 Results of load identification in each scenario

由表5 可知，本文提出的基于單通道盲源分離的非侵入式工業諧波干擾設備識別方法是可行的，該方法在僅有電網側三相電壓和電流數據的情況下，可有效地識別工業用戶所包含的諧波源負荷類型，具有較好的工程實用性和適應性。

4.2 實測算例分析

以某變電站35 kV母線上的一條帶有大量高度非線性工業負荷的支路為例，采集在12.8 kHz采樣頻率下的三相電壓和電流數據，并對其A相電壓和電流數據進行計算，得到該支路的綜合等值阻抗參數R和X，如圖11所示。

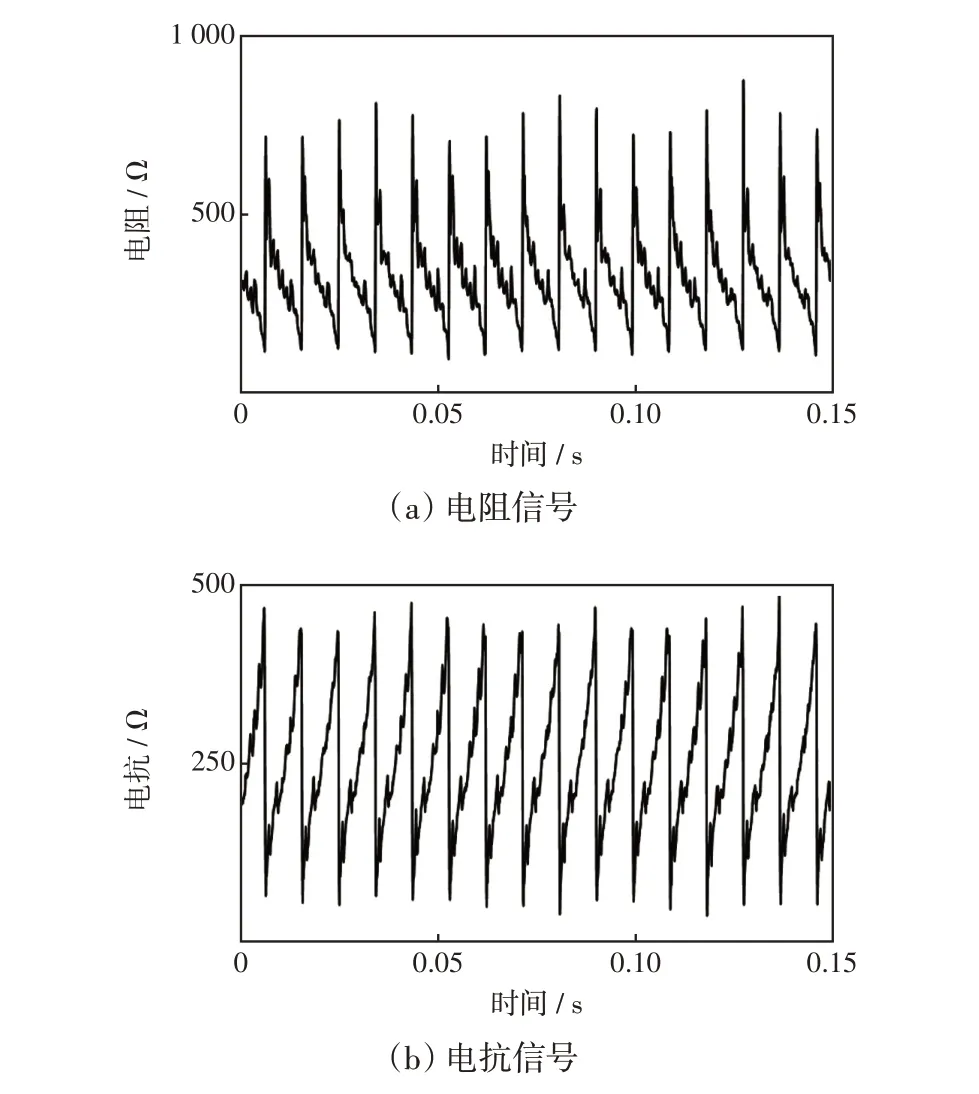
圖11 支路綜合等值阻抗參數Fig.11 Integrated equivalent impedance parameters of branch

由圖11 可以看出，該支路的綜合等值阻抗參數值波動較大，其所帶負荷給35 kV 母線注入大量的諧波。考慮到該母線帶有一定容量的治理裝置，會對阻抗信號造成一定的影響，因此本文判斷諧波源負荷類型時以受影響較小的電阻信號為主，分離得到的電阻信號波形如圖12所示。本文將噪聲信號當作一個獨立源信號處理，以消除數據采集過程中噪聲的影響。

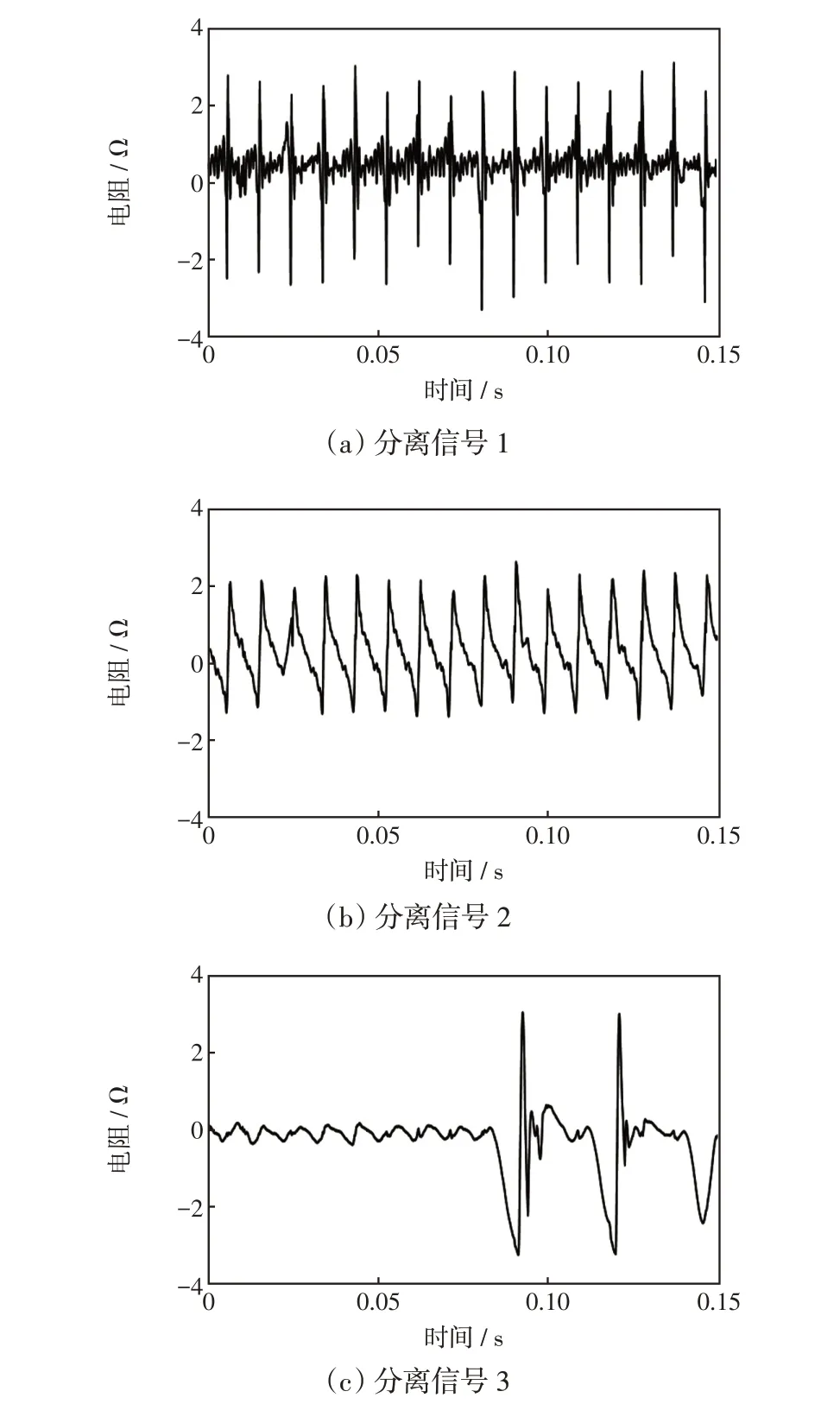
圖12 電阻信號的分離結果Fig.12 Separation result of resistance signal

由圖12 及工業用戶的阻抗特性可得，分離信號1 可認為是電弧爐負荷；分離信號2 則可認為是整流型負荷；而分離信號3可認為是噪聲信號。該結果與實際情況，即35 kV 母線支路所帶負荷主要是電加熱負荷，包括小功率電弧爐、感應加熱爐是一致的，說明本文所提出的非侵入式分解方法能用于工業用戶的諧波源負荷識別，且具有較好的適用性和實用性。同時表明，本文方法在存在治理裝置及噪聲的情況下，亦可識別工業用戶的諧波源負荷類型，具有一定的工程實際應用價值。

5 結論

本文研究了一種基于單通道盲源分離的非侵入式工業諧波干擾設備識別方法，具有以下優勢。

（1）在無法檢測負荷啟停狀態、事件突變等暫態過程或獨立運行狀態的情況下，僅依據電網側供電支路的三相電壓和電流數據，即可辨識工業用戶諧波源負荷的類型，不受負荷容量影響，便于供電公司對大量接入的工業用戶諧波源進行實時精細化管控；能及時識別諧波源投運工況并發現潛在諧波超標風險，具有較好的可移植性和工程實用性。

（2）本文將改進后的CLMD 算法與復值FastICA 算法相結合，實現復數域信號的單通道盲源分離，并將其應用于工業用戶諧波干擾設備的識別中，具有較好的可行性和適應性，為將來非侵入式數據分解方法在工業負荷識別方面的應用提供新的思路。

本文提出的工業用戶諧波源負荷非侵入式識別方法在未來可用于企業負荷工況檢測等方面，對于企業節能潛力的挖掘、異常用電分析等場景具有廣闊的應用前景；根據額外的數據信息，例如用戶用電量等數據，即可對本文方法進行擴展，以進一步識別出屬于同類諧波源負荷的多種用電設備的具體類型。