斜爆轟波總壓規律及其在爆轟發動機分析模型中的應用1)

黃 恩 史愛明

(西北工業大學航空學院,西安 710072)

引言

隨著各大國高超聲速飛行器的競爭式發展,更高飛行馬赫數以及更強機動性能已經成為重要發展方向[1].在探索研究動力推進系統的過程中,爆轟燃燒推進因具有熱循環效率高、燃燒速率快等優點[2-3],逐漸顯露出將取代傳統動力技術的趨勢.目前基于爆轟燃燒推進的發動機主要包括: 脈沖爆轟發動機、旋轉爆轟發動機以及斜爆轟發動機.這3 種爆轟發動機有著各自不同的工作特點和適用區間[4-6],具有較強的應用前景.

作為爆轟燃燒推進的重要組成部分,斜爆轟波受到了重點研究,至今已積累了可觀的研究成果[7-10].其中很大部分的研究重點關注于起爆區的波系組成以及爆轟波面的燃燒組織.對于前者,研究發現起爆過程,即斜激波過渡到斜爆轟波的過程可分為突變過渡和彎曲過渡[11].而來流參數、幾何參數和化學參數都會影響起爆區的波系結構[12-14].對于后者,小尺度波系的形成和演化過程以及斜爆轟波面穩定性得到了細致研究[15-17].為加快斜爆轟波的工程應用進程,非均勻來流條件下的斜爆轟波結構[18-20]、受限空間的爆轟波駐定特性[21-23]以及斜爆轟發動機的推力性能[24]等實際問題在近幾年逐漸受到關注.

作為衡量氣體做有用功能力的表征量[25],氣流總壓在動力系統中一直是個實際而又重要的參數.對動力系統而言,更小的總壓損失意味著更大的推力潛力.對于超聲速氣流中斜激波的總壓規律,史愛明等[26]基于斜激波極曲線方法,在斜激波全解域中發現了最小總壓損失直線規律,并給出了斜激波總壓損失律圖解.通過斜激波總壓損失律圖解,可以快速確定當前楔面角度下滿足最小總壓損失的斜激波結構,為提高動力系統效率提供了一種具有應用前景的理論參考.而對于以爆轟波為基礎的爆轟推進系統,斜激波的總壓損失律圖解顯然失去直接效用.因此有必要補充研究斜爆轟波的總壓特性.由于研究的是已正常工作的爆轟發動機,此時斜爆轟波應是得到充分發展并穩定的,因此本文主要關注于已經形成的、穩定的斜爆轟波面,而爆轟起爆過程的波系結構以及波面失穩情況不在本文研究范圍.

與絕熱斜激波類似,斜爆轟波同樣存在極曲線方法.忽略化學反應非平衡過程,即認為化學反應速率無限大、放熱在瞬間完成,那么便可借鑒斜激波極曲線分析方法,推導出斜爆轟波極曲線方程,進而用于分析斜爆轟波特性[8].此時,斜爆轟波被簡化為含有瞬時能量添加的斜激波.盡管真實條件下的斜爆轟波結構遠比簡化模型復雜,但斜爆轟波總壓屬于宏觀特性的研究,而簡化后的極曲線分析方法更是提供了全解域的研究視角.因此,本文將利用斜爆轟極曲線方法,從全解域的角度分析理想狀態下的斜爆轟波總壓特性,期望在概念設計階段為斜爆轟發動機的設計提供參考.

1 斜爆轟極曲線方法

1.1 理想假設

(1) 忽略化學反應非平衡過程,假設化學反應速率無限大;

(2) 激波前后比熱比γ以及氣體常數R保持不變,無特殊說明,本文采用γ=1.3.

1.2 斜爆轟波關系式

本文以無量綱參數作為公式推導以及討論的變量,因此首先定義如下無量綱參數

式中,q為單位質量氣體在爆轟中釋放的熱量,u為氣流垂直于斜爆轟波的速度分量,a為當地聲速,a*為臨界聲速,ρ為氣體密度,p為氣體壓強,T為氣體溫度,Δp0為波后總壓損失值;下標1,2 分別代表波前波后靜參數,而下標01,02 則分別代表波前波后總參數.

根據假設,斜爆轟波波后流動參數可得[8]

式中,γ為氣體比熱比,θ為氣流偏轉角,β為斜爆轟角,Mn1為斜爆轟波前法向馬赫數.

當Q=0 時,可以證明方程(2)將退化為絕熱斜激波關系式,這意味著斜爆轟波關系式具有一定普適性.

在方程(2)的基礎上,若以波前法向馬赫數作為斜爆轟波強度表征量,則可通過三角公式變換得到斜爆轟波強度表達式

值得注意的是,式(3)同時適用于式(2)中第一行出現的兩個數學解,是用于計算斜爆轟波強度的控制方程.關于θ和β的顯式表達式是評估爆轟波幾何結構對爆轟強度影響的有效手段.當激波絕熱(Q=0)時,其乘積右項等于1,此時式(3)與絕熱斜激波強度表達式完全一致[26].此外,式(3)還體現出波前法向馬赫數必須大于 1 的物理限制.

同時經推導可以得到描述斜爆轟波的廣義普朗特關系式

當無熱量產生時,式(4)便自然退化為絕熱條件下的普朗特關系式[25](a*2=u1·u2).此外,它直接揭示了斜爆轟波與絕熱斜激波之間的本質區別——波前波后臨界聲速不等,即焓值發生改變.

波后法向馬赫數可由質量守恒方程導出

式中,Mn2為波后法向馬赫數,M2為波后馬赫數.

至此,斜爆轟波前后流動參數關系式都已得到,這些關系式將作為基本方程用于研究斜爆轟波的總壓規律.

1.3 斜爆轟波極曲線

由于存在熱量的釋放,斜爆轟波極曲線不再與絕熱斜激波極曲線相同.圖1 展示了絕熱斜激波與斜爆轟波極曲線之間的聯系.絕熱斜激波極曲線對于相同楔面角度存在雙解,分別代表斜激波的強解(上)與弱解(下);而斜爆轟波極曲線中不僅存在強弱斜爆轟波,其弱斜爆轟波還存在著兩個分支.結合式(2)中出現的正負號,正號對應著圖中左側虛線,代表著欠驅動斜爆轟波(underdriven),其波后法向馬赫數大于1;而負號對應著右側實線,象征著過驅動斜爆轟波(overdriven),其波后法向馬赫數小于1.兩分支的分界點被稱為Chapman-Jouguet (CJ)點,此時波后法向馬赫數等于1.由于波后法向馬赫數小于1 是斜爆轟波附著穩定的必要條件,楔面角度需要滿足θcj＜θ＜θmax,這段區間被稱為駐定窗口[27].

圖1 斜爆轟波與斜激波極曲線之間的差異Fig.1 The difference between the polars of oblique detonation wave and oblique shock

2 結果與討論

2.1 斜爆轟波最弱強度規律

對于斜爆轟波,因為忽略非平衡過程,其化學反應產生的影響可以通過反應后的氣體狀態量表征.當反應足夠充分,可以根據來流成分比例、溫度以及速率等推測出化學反應所產生的熱量,進而計算出斜爆轟波關系式中重要的無量綱熱量Q[28].將具體的化學反應過程抽象為無量綱熱量Q,使得斜爆轟波的理論研究不局限于某一特定化學反應.因此,為了更好展現斜爆轟波的特征規律,本文將適當選取Q值大小.

當Q值大小不變時,根據斜爆轟波極曲線關系式,可以得到一組極曲線族,如圖2 所示.于是CJ 點共同組成一條CJ 曲線.CJ 曲線的存在是斜爆轟波極曲線與斜激波極曲線的標志性區別,且CJ 曲線的控制方程如下

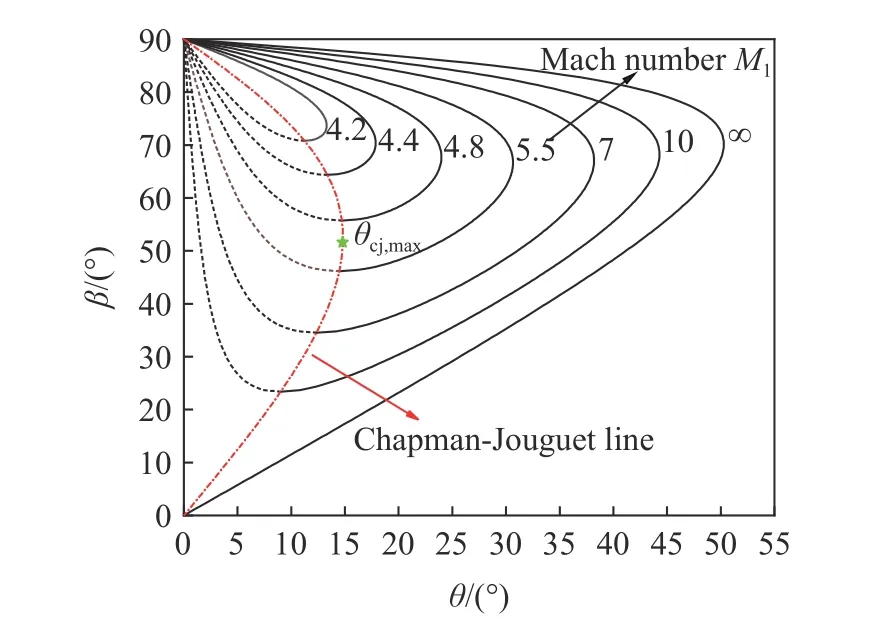
圖2 一組斜爆轟波極曲線(Q=10)Fig.2 A set of oblique detonation wave polars (Q=10)

式中,下標cj 代表CJ 曲線上的流動參數.顯然CJ 曲線是一條等爆轟波強度曲線,并且曲線形狀與Q值大小直接相關.

CJ 曲線是當前Q值下的全局最弱強度解.CJ 點是爆轟波極曲線的最低點,此時爆轟角最小,計算出的法向馬赫數也最小,這意味著CJ 點是該極曲線上的最弱強度解.而CJ 曲線由CJ 點連接而成,且強度相等.由此可得,CJ 曲線是當前Q值下的最弱爆轟波強度解.此外,當斜爆轟波位于CJ 點時,斜爆轟波導致的熵增最小[29].在斜爆轟發動機的設計中,氣流速度大于CJ 速度滿足駐定條件的前提下,也會盡可能去靠近CJ 點[30-31].也就是說,CJ 曲線對斜爆轟發動機的設計十分重要.

然而當楔面角大于θcj,max時,無法取得CJ 點,此時斜爆轟的強度規律需要進一步研究.為此我們取極限情況,令楔面角度等于θcj,max,于是直線θ=θcj,max與CJ 曲線相切,由于CJ 曲線是斜爆轟波的全局最弱解,顯然該相切點,即CJ 曲線的極值點便是當前楔面角度的局部最弱解.通過進一步改變Q值大小,CJ 曲線形狀也隨之改變,如圖3 所示.圖中繪制了Q值從0 均勻變化到10 的CJ 曲線形狀,可以發現在Q較小時,CJ 曲線形狀變化劇烈,相同的Q值變化會導致更大的欠驅動斜爆轟波區域變化,而隨著Q值增加,CJ 曲線形狀的變化程度迅速減小.圖中★表示CJ 曲線的極值點,發現隨著Q值增加,極值點在直線β=θ/2+π/4 上移動.而CJ 曲線的極值點代表著θ=θcj,max的局部最弱解,這意味著對于θ＞θcj,max的局部最弱解會存在相同的規律.

圖3 不同Q 值下的CJ 曲線Fig.3 CJ curves with different Q values

于是為了證明這一規律,通過對公式(3)求導并計算極值,發現當斜爆轟波結構滿足以下關系時,斜爆轟波強度最小

式中,βext為最弱斜爆轟波所對應的爆轟角.這與CJ 曲線極值點的移動規律一致.

此外,式(8)與絕熱斜激波的最弱激波直線方程一致[26].也就是說,最弱激波直線方程(8)同時適用于絕熱斜激波和非絕熱斜爆轟波.

圖4 展示了Q=10 時斜爆轟波的強度變化規律.當楔面角度大于等于θcj,max時,斜爆轟波以方程(8)為最弱強度解,而爆轟角增加或減小都會使得爆轟波強度增加.而當楔面角度小于θcj,max時,由于部分解為欠驅動斜爆轟波,無法穩定存在,此時CJ 解便是當前楔面角度的最弱解,也表征著當前Q值的爆轟波強度下界.此外,隨著楔面角度的增加,最弱爆轟波強度直線上所對應的強度也會增加.

圖4 極曲線圖譜上的斜爆轟波強度規律(Q=10)Fig.4 The law for oblique detonation wave intensity on the polar curves (Q=10)

2.2 最小總壓損失律擴展

對絕熱斜激波而言,激波強度與總壓損失一一對應,當激波強度達到最小時,其造成的總壓損失也達到最小[26].而對于斜爆轟波,由于存在能量釋放,會對其強度以及總壓特性產生影響.觀察斜爆轟波強度方程(3)可以發現,由于氣體爆轟所釋放的無量綱熱量Q,斜爆轟波整體強度會高于絕熱斜激波.根據2.1 節的討論,斜爆轟波的最弱強度規律并不會改變,但是對于斜爆轟波的總壓損失規律還需要進一步的討論.

下面將細致分析斜爆轟波總壓損失規律,不過與絕熱斜激波不同,斜爆轟波總壓損失律還與Q值相關.經推導簡化,發現總壓損失律可表示為關于Mn1,γ,Q的函數,且表達式十分復雜,這里采用圖解方法

式中,Δ代表著斜爆轟波后的總壓損失率.于是可通過式(9)計算出斜爆轟波導致的總壓損失.

圖5 展示了Q=2 時斜爆轟波的總壓損失極值.從整體上看,當固定楔面角(氣流偏角)時,每條總壓損失曲線確實存在唯一的極小值點,在圖中標記為紅色小球.且隨著楔面角度增加,其造成的整體總壓損失水平也相應增加.從局部上看,每個楔面角所對應的總壓損失極值點在θ-β平面上的投影構成了一條總壓損失極小值曲線,可以發現該曲線與絕熱斜激波極小值線之間存在一定偏移,這種偏移隨著楔面角的增加而減小,在40°楔面角時偏移幾乎為0.這是因為當楔面角較大時,其誘導的絕熱斜激波造成的總壓損失已經達到相當高的水平,此時,爆轟燃燒釋放的熱量對氣流總壓所能影響的程度大幅減小.

圖5 總壓損失極小值線(紅色實線: Q=2 的斜爆轟波;綠色實線:斜激波)Fig.5 The curve of minimum total pressure loss for oblique detonation wave (Q=2,solid red line) and oblique shock wave (solid green line)

顯然,與絕熱斜激波不同,斜爆轟波的最弱激波規律不再等價于最小總壓損失.Q值的存在使得二者之間發生偏移.從公式推導的角度來看,當Q=0時,總壓損失表達式是關于波前法向馬赫數的單調函數[26],二者相互等價.然而當Q＞ 0 時,此時總壓損失不僅與波前法向馬赫數有關,還與Q值有關,根據方程(2)可知Q與Mn1相互乘積耦合,這導致與Q=0 時相比,新增的Mn1項使得總壓損失表達式對法向馬赫數求導的結果改變,不再隨法向馬赫數單調變化.這意味著總壓損失極值與最弱激波之間發生偏移.而從物理參數角度分析,波前法向馬赫數僅與波前流動參數有關;而根據公式(9)可知,總壓損失會同時受到波前波后流動參數的影響.當Q=0時,波前波后總溫和臨界聲速相等,波前波后基準統一,此時總壓損失大小與激波強度能相互表征.而當Q＞ 0 時,爆轟波不再滿足絕熱條件,波前波后總溫以及臨界聲速發生改變,波前波后的基準不再相同,總壓損失極值與最弱激波之間的對應關系被打破,于是出現偏移現象.

圖6 給出20°楔面角下Q值對偏移量的影響.當激波絕熱時,總壓損失律呈現出對稱性質,在對稱面55°(激波角)得到極小值,此時滿足絕熱斜激波總壓損失極小值控制方程[26].然而當Q值增加,總壓損失對稱性質被打破,極值點向更大的激波角方向偏移.Q值較小時,這種偏移敏感度更加明顯,例如Q從0 增加至2 就會導致極小值9°左右的偏移.此外,隨著Q值增加,爆轟波強度的整體水平上升,進一步造成更高的總壓損失水平.

圖6 不同Q 值下總壓損失與激波角的關系(20°楔面角)Fig.6 The relation between total pressure loss and shock angle at different Q values (when the wedge angle is 20°)

圖7 借用激波角進一步展示了總壓損失極小值偏移隨Q值的變化情況.從圖上看,紅色實線表示最小總壓損失,藍色實線則代表著最弱爆轟波強度.而二者所對應的激波角差值則代表著偏移程度.當激波絕熱時,二者重合,此時不發生偏移;而隨著Q值的增加,二者的偏移將以一個非常大的斜率迅速增加,然后逐漸減緩直至收斂.這意味著Q值對斜爆轟波結構的影響效率會隨著Q值增加而減小,換而言之,斜爆轟波結構對Q的敏感程度與Q值大小成負相關.

圖7 不同Q 值下的最小總壓損失和最弱爆轟波強度(20°楔面角)Fig.7 The minimum total pressure loss and the weakest detonation wave strength at different Q values (when the wedge angle is 20°)

綜上,對斜爆轟波而言,盡管總壓損失律的對稱性被打破,但極小值點仍舊存在,氣體爆轟燃燒導致的極值偏移現象隨Q值增大而加劇,但偏移速度迅速降低.

2.3 應用舉例

假設有一臺在任意馬赫數下都可以啟動的斜爆轟發動機,如圖8(a)所示,燃料與來流空氣充分混合并在15°楔面產生斜爆轟波,假定燃料充分燃燒且化學反應速率無限快,爆轟產生的高壓氣體經過等熵膨脹至環境反壓,高速的尾流產生推力.那么為使發動機有盡可能大的推力上限,應控制進入發動機的氣流馬赫數為多少？

圖8 斜爆轟發動機工況設計的最優馬赫數選取過程Fig.8 The operating process of selecting an optimum Mach number for oblique detonation engine design

發動機要產生更大的推力,經過等熵膨脹后噴射出飛行器尾部的爆轟氣流速度應盡可能大,由于來流的總壓一定,經過斜爆轟波的總壓損失會直接影響著尾噴的氣流速度.因此選取的來流馬赫數應盡可能使氣流總壓損失最小,選取步驟如下: (1) 根據注入的燃料當量比以及進入發動機的流動參數計算出爆轟波產生的無量綱熱量Q(這里假定為2);(2) 利用圖8(b)讀取15°楔面角對應的最小總壓損失0.491 及對應的斜爆轟角67.5°;(3) 使用式(3)計算此時對應的來流馬赫數為2.394.

然而事實上,對于斜爆轟發動機,幾乎不可能在如此低的馬赫數下正常工作[32].如果考慮爆轟發動機能夠工作的馬赫數要求,選取步驟只需增加一定的馬赫數限制.根據方程(2),斜爆轟發動機工作的馬赫數區間可以轉化為固定楔面角下的爆轟角區間,于是在圖8(b)中便能劃出斜爆轟波的總壓損失區間,進而選取滿足爆轟發動機工作條件的最小總壓損失.

當然,在真實的斜爆轟發動機中由于存在極其復雜的波系相互作用,例如膨脹波與斜爆轟波相互作用、邊界層與爆轟波相互作用等,使得斜爆轟發動機產生的總壓損失總量會與本案例中計算出的僅由斜爆轟波產生的總壓損失值之間存在很大差異.但是斜爆轟波作為斜爆轟發動機中不可或缺的核心流動結構,其造成的總壓損失可以用于衡量斜爆轟發動機的總壓極限.在概念設計中選擇造成總壓損失盡可能小的斜爆轟波結構,可提高發動機的總壓理論上限,增加發動機的推力潛力,有利于后續的詳細設計甚至優化設計.

3 結論

本文主要針對斜爆轟波總壓損失問題,利用斜爆轟極曲線方法,在激波全解域上分析討論了斜爆轟波的總壓特性,主要結論如下.

(1) 分析了斜爆轟波的最小總壓損失律,利用圖解方法證明了斜爆轟波總壓損失極小值的存在性.與絕熱激波相比,氣體爆轟釋放的熱量使得爆轟波強度整體增加,進而導致總壓損失極小值向更大的爆轟角偏移,其偏移程度與楔面角呈負相關,與釋放的熱量大小呈正相關.

(2) 推導出斜爆轟波強度關系式,爆轟角β與楔面角θ滿足直線方程β=θ/2+π/4 時,斜爆轟波強度最小,與絕熱斜激波強度最弱關系式一致.這說明對于非絕熱的斜爆轟波,最弱激波直線規律同樣存在.

(3) 利用激波極曲線族,指出Chapman-Jouguet 曲線是一條等強度曲線,且具有全局最小爆轟波強度的性質.

本文將絕熱的斜激波總壓損失問題拓展至非絕熱的斜爆轟波,延伸出的非絕熱斜爆轟波總壓損失律有利于在斜爆轟發動機概念設計階段中獲得較大的總壓上限,益于后續的詳細設計乃至設計優化.

數據可用性聲明

支撐本研究的科學數據已在中國科學院科學數據銀行ScienceDB (science data bank)平臺公開發布,訪問地址為https://doi.org/10.57760/sciencedb.09411 或https://cstr.cn/31253.11.sciencedb.09411