激波內(nèi)部結(jié)構(gòu)的數(shù)值求解方法1)

朱清波 周文元 楊慶春 徐 旭

* (北京航空航天大學(xué)宇航學(xué)院,北京 102206)

? (上海空間推進(jìn)研究所,上海 201112)

引言

在氣體動(dòng)力學(xué)中,激波常被簡(jiǎn)化為零厚度的間斷面,經(jīng)過激波,流動(dòng)參數(shù)發(fā)生階躍,熵不可逆地增加,這對(duì)大部分情況是很好的近似.然而真實(shí)的宏觀流動(dòng)中不會(huì)出現(xiàn)數(shù)學(xué)意義上的不連續(xù),激波也不例外,從波前向波后狀態(tài)的過渡必然是連續(xù)的,而激波厚度則是一個(gè)有限值.圖1 展示了一個(gè)典型駐定正激波的內(nèi)部流動(dòng)參數(shù)變化曲線,其中Ma1和Ma2分別為波前和波后馬赫數(shù),δ 為基于最大速度梯度定義的激波厚度.

圖1 激波內(nèi)部結(jié)構(gòu)示意圖Fig.1 Schematic diagram of the internal structure of shock waves

研究激波內(nèi)部流動(dòng)參數(shù)變化過程的問題被稱為激波結(jié)構(gòu)問題,它不僅是一個(gè)重要的科學(xué)問題,還具有工程實(shí)用價(jià)值.在稀薄氣體動(dòng)力學(xué)[1]、分子動(dòng)理論[2]、非平衡態(tài)熱力學(xué)[3]和天體物理[4]等基礎(chǔ)科學(xué)領(lǐng)域中,激波結(jié)構(gòu)問題促進(jìn)了對(duì)激波、輸運(yùn)現(xiàn)象以及流體力學(xué)理論基礎(chǔ)的理解.在航空航天[5-6]、光學(xué)[7]以及核[8]等技術(shù)領(lǐng)域中,激波結(jié)構(gòu)的正確解析對(duì)解決一些工程問題至關(guān)重要.例如航天器再入[5-6]時(shí),高層大氣極其稀薄導(dǎo)致激波厚度較大,準(zhǔn)確模擬激波內(nèi)部結(jié)構(gòu)是外流場(chǎng)仿真的關(guān)鍵之一;又比如,激波會(huì)使光發(fā)生偏折,正確描述激波結(jié)構(gòu)有助于修正它對(duì)光學(xué)系統(tǒng) (風(fēng)洞試驗(yàn)的光學(xué)測(cè)量裝置、超聲速飛行器的光學(xué)觀瞄設(shè)備與機(jī)載激光武器等) 產(chǎn)生的不利影響[7].此外,駐定正激波是一個(gè)一維定常且邊界條件極其簡(jiǎn)單的強(qiáng)非平衡流動(dòng),這使其成為驗(yàn)證氣體動(dòng)力學(xué)模型及相關(guān)數(shù)值方法準(zhǔn)確性與可靠性的理想場(chǎng)景,再加上豐富的實(shí)驗(yàn)數(shù)據(jù)[9-10],激波結(jié)構(gòu)長(zhǎng)期被用作嚴(yán)苛而敏感的標(biāo)準(zhǔn)測(cè)試算例[11-14].

激波結(jié)構(gòu)的求解有解析和數(shù)值兩種方式.一般來說,包括激波結(jié)構(gòu)問題在內(nèi)的大部分流動(dòng)問題非常復(fù)雜,難以求得解析解.但Becker[15]發(fā)現(xiàn)當(dāng)氣體的Prandtl 數(shù)等于3/4 這個(gè)特殊值時(shí),激波內(nèi)部流動(dòng)所滿足的能量方程可以被簡(jiǎn)化,總焓沿流向保持不變,進(jìn)而獲得了第一個(gè)對(duì)任意強(qiáng)度激波有效的解析解.Becker 解隨后被不斷改進(jìn),從最初的只適用于輸運(yùn)系數(shù)為常數(shù)的氣體,到適用于硬球和Maxwell 分子模型氣體[16]、軟球分子模型氣體[17]和van der Waals 氣體[18]等.盡管適用范圍不斷擴(kuò)大,這些解析解對(duì)Prandtl 數(shù)的要求卻從未放寬.另一個(gè)被廣泛使用的解析解是Mott-Smith[19]提出的著名的雙峰分布函數(shù)解,然而它只是一定假設(shè)下的近似解,且從原理上看不能很好地描述弱激波.實(shí)際上,即使對(duì)強(qiáng)激波,Mott-Smith 解也不被實(shí)驗(yàn)和直接模擬Monte Carlo(DSMC) 計(jì)算的結(jié)果支持[10].總而言之,目前的解析方法仍存在較多局限性,只能解決一些特殊條件下的簡(jiǎn)單問題,而大部分激波結(jié)構(gòu)問題較為復(fù)雜,需借助數(shù)值方法求解.

隨著計(jì)算科學(xué)的發(fā)展,數(shù)值技術(shù)在流體力學(xué)中發(fā)揮著越來越重要的作用,激波結(jié)構(gòu)問題也受益于此.按所采用的數(shù)學(xué)物理模型的類型來劃分,激波結(jié)構(gòu)的數(shù)值模擬方法主要有3 種:

(1) 微觀方法,即基于還原論觀點(diǎn)、從第一性原理出發(fā)直接模擬分子運(yùn)動(dòng)和碰撞的粒子方法,主要包括以分子動(dòng)力學(xué)[20](MD) 為代表的確定論方法和以DSMC[21-22]為代表的概率方法;

(2) 介觀方法,求解基于速度分布函數(shù)描述的Boltzmann 方程[23-24],或其簡(jiǎn)化方程/模型[25],包括著名的BGK 模型方程[26]和離散速度模型[27-28](DVM) 等;

(3) 宏觀方法,求解基于宏觀量描述的連續(xù)介質(zhì)流體力學(xué)方程/模型,包括經(jīng)典和改進(jìn)的Navier-Stokes 方程[11,29-30]、以Burnett 方程為代表的高階流體力學(xué)方程[31-32]、Grad 矩方程及其變體[14,33]、廣義流體力學(xué)[34](generalized hydrodynamics) 方程、非線性耦合本構(gòu)關(guān)系[35](NCCR) 模型以及擴(kuò)展/廣延熱力學(xué)[3](extended thermodynamics) 模型等.

相對(duì)于Boltzmann 方程,控制氣體宏觀運(yùn)動(dòng)的流體力學(xué)方程是一種降階的描述,自由度更少,因而更簡(jiǎn)單.例如在Chapman-Enskog 理論[36]中,Navier-Stokes 方程和Burnett 方程分別是對(duì)Boltzmann 方程的一階和二階近似.因此,第3 類方法原則上應(yīng)歸入第2 類.但從介觀Boltzmann 方程到宏觀流體力學(xué)方程的粗化并不容易,兩者之間的關(guān)系在數(shù)學(xué)上也遠(yuǎn)非顯而易見 (詳見Hilbert 第6 問題[37]).更重要的是,流體力學(xué)方法基于與分布函數(shù)描述迥然不同的局部統(tǒng)計(jì)平均量 (分布函數(shù)的矩) 描述,體系相對(duì)獨(dú)立而內(nèi)容又極其豐富,故單獨(dú)列為一類.

前述3 類方法中,基于流體力學(xué)方程的數(shù)值模擬最受青睞,因?yàn)樗诰哂辛己镁鹊耐瑫r(shí)還有較高的計(jì)算效率,其宏觀描述也為人們樂于接受,因此相關(guān)算法得到高度發(fā)展.具體到激波結(jié)構(gòu)的仿真計(jì)算中,有限差分法常被使用,這類通用的計(jì)算流體力學(xué)技術(shù)十分成熟,此處不再贅述.

由于以下3 個(gè)原因,絕大多數(shù)激波結(jié)構(gòu)問題可歸結(jié)為一維定常正激波的結(jié)構(gòu)問題.

(1) 激波的典型厚度非常小,流體穿過激波的時(shí)間極短,一般僅需數(shù)次分子碰撞即可完成從波前到波后狀態(tài)的過渡,弛豫速度遠(yuǎn)快于其他宏觀非平衡流動(dòng)現(xiàn)象.因此,對(duì)于大部分激波結(jié)構(gòu)問題,運(yùn)動(dòng)隨時(shí)間的發(fā)展不重要,非定常效應(yīng)可以忽略.

(2) 平面激波流動(dòng)可以被視為法向的正激波流動(dòng)疊加切向的平行流動(dòng).因此,二維或三維平面激波的結(jié)構(gòu)問題可被簡(jiǎn)化為法向上的一維正激波結(jié)構(gòu)問題.

(3) 曲面激波波面的最小曲率半徑一般遠(yuǎn)大于激波厚度,所以曲率對(duì)激波內(nèi)部結(jié)構(gòu)的影響通常可以忽略,曲面激波的局部可被近似為平面激波,進(jìn)而分解為法向上的正激波和切向的平行流.

毫無疑問,一維定常正激波是檢驗(yàn)氣體動(dòng)力學(xué)模型 (尤其是稀薄氣體動(dòng)力學(xué)模型) 的理想算例: 極小的厚度意味著Knudsen 數(shù)較大,間斷分子效應(yīng)顯著;強(qiáng)耗散意味著遠(yuǎn)離熱力學(xué)平衡,非平衡效應(yīng)顯著;一維定常的特性和簡(jiǎn)單的邊界條件還降低了問題的復(fù)雜性.定常正激波的結(jié)構(gòu)問題,其本質(zhì)是求解一組流體力學(xué)常微分方程.對(duì)這類問題,直接數(shù)值積分比有限差分法更簡(jiǎn)單高效.然而對(duì)激波結(jié)構(gòu)應(yīng)用空間推進(jìn)的數(shù)值積分仍存在一些問題,例如沿流向推進(jìn)計(jì)算的發(fā)散問題,本文的目的是解決這些問題,并建立在流體力學(xué)框架內(nèi)數(shù)值求解激波結(jié)構(gòu)的一般程序.

由于關(guān)注的問題具有普遍性,本文將只討論最基礎(chǔ)的情況,即單組分簡(jiǎn)單氣體的情況,多組分氣體和等離子體的情況暫不考慮,以避免不必要的細(xì)節(jié)把問題復(fù)雜化.控制方程將采用簡(jiǎn)單的Navier-Stokes 方程,這不會(huì)導(dǎo)致本文的討論失去一般性,因?yàn)楹暧^連續(xù)的流體系統(tǒng)都具有Navier-Stokes 形式的守恒方程,區(qū)別僅在于用怎樣的本構(gòu)方程封閉它們,而這不影響本文的主要結(jié)論.

1 控制方程與邊界條件

一維氣體流動(dòng)的質(zhì)量、動(dòng)量和能量守恒方程分別可寫為

其中,t,x,ρ,V,p,u,ht,τ 和q分別為時(shí)間、流向坐標(biāo)、密度、速度、壓強(qiáng)、比內(nèi)能、比總焓、黏性應(yīng)力以及熱流密度.需要說明的是,為保持與氣體運(yùn)動(dòng)論領(lǐng)域的習(xí)慣一致,本文約定當(dāng) τ 表現(xiàn)為壓應(yīng)力時(shí)其符號(hào)為正,這與流體力學(xué)中法向應(yīng)力的定義相反.式(1)～式(3) 直接來源于三大守恒定律,也可從Boltzmann 方程的矩方程——Maxwell 輸運(yùn)方程導(dǎo)出,未對(duì) τ 和q作任何假設(shè),因此被所有連續(xù)介質(zhì)氣體動(dòng)力學(xué)模型的一維形式所遵守.

若采用Navier-Stokes 和Fourier 線性本構(gòu)關(guān)系,有

式中,T是溫度,μ 和 κ 分別為動(dòng)力黏度和導(dǎo)熱系數(shù).將式 (4) 代入式(1)～式(3) 即得到一維可壓Navier-Stokes 方程組.

考慮如圖1 所示的坐標(biāo)系固定在波面上的駐定正激波情況,由于流動(dòng)是定常的,時(shí)間偏導(dǎo)項(xiàng)為0,所有參數(shù)僅與位置x有關(guān),式(1)～式(3) 可簡(jiǎn)化為常微分方程,將所得常微分方程對(duì)x積分,得到一維定常正激波內(nèi)部流動(dòng)的控制方程

式中,Jm,JP和JE是積分常數(shù),不隨x改變.實(shí)際上它們分別是質(zhì)量、動(dòng)量和能量的通量,并且因?yàn)樵诓ㄇ安ê鬅o窮遠(yuǎn)處 τ 和q趨于0,根據(jù)式(5)～式(7)顯然有

下標(biāo)1 和2 分別表示上游和下游無窮遠(yuǎn)處的狀態(tài).

進(jìn)一步引入理想氣體狀態(tài)方程

其中R為氣體常數(shù).式(4)～式(7) 與式(11) 組成一個(gè)封閉的微分方程組,從中消去 τ,q,p以及 ρ 可得

該系統(tǒng)滿足以下漸近邊界條件

其中V2和T2可根據(jù)來流參數(shù)V1,T1以及正激波前后參數(shù)的關(guān)系求出.

2 打靶法

式 (12)～式(13) 構(gòu)成一個(gè)封閉的一階常微分方程組,沿x對(duì)其積分可獲得V和T的沿程分布.然而邊界條件 (14) 給在無窮遠(yuǎn)處,無法在數(shù)值積分中直接使用,人們很自然地想到將無限域截?cái)喑捎邢薜挠?jì)算域,再用打靶法[6,30,38]將邊值問題轉(zhuǎn)化為初值問題求解,其具體步驟如下.

(1) 選一略小于V1的速度值,將其對(duì)應(yīng)的位置作為積分的起點(diǎn),坐標(biāo)指定為x=0,該速度值記為V(0).

(2) 選一略大于T1的溫度值作為T(0) 的猜測(cè)值.

(3) 以V(0) 和T(0) 為初值,對(duì)式(12)～式(13) 構(gòu)成的系統(tǒng)進(jìn)行數(shù)值積分,積分沿著流動(dòng)的方向進(jìn)行,向下游推進(jìn)足夠遠(yuǎn)后截?cái)?

(4) 若第3 步積分出的V和T的曲線像圖1 給出的分布曲線那樣逐漸趨平,則結(jié)束計(jì)算并輸出結(jié)果;若積分過程中發(fā)散或出現(xiàn)參數(shù)明顯遠(yuǎn)離波后值的趨勢(shì),則中斷計(jì)算、修正T(0) 的值并回到第3 步.

第1 步的目的是對(duì)計(jì)算域的上游邊界進(jìn)行人工截?cái)?第3 步可采用各種數(shù)值積分算法,包括但不限于Runge-Kutta 法;第4 步的目的是對(duì)與V(0) 相對(duì)應(yīng)的初值T(0) 進(jìn)行迭代修正.不同文獻(xiàn)使用的算法在細(xì)節(jié)上可能有所差異,例如文獻(xiàn) [6,30,38] 直接求解的變量是p和 ρ,積分的起始點(diǎn)則選在p=(p1+p2)/2處,并從該點(diǎn)分別向上下游推進(jìn),這些文獻(xiàn)的方法與本節(jié)的方法沒有本質(zhì)區(qū)別.

2.1 打靶法的失效

用前述的打靶法對(duì)單原子氣體中Ma1=2 的正激波結(jié)構(gòu)進(jìn)行了求解,數(shù)值積分采用自適應(yīng)步長(zhǎng)的4 級(jí)Runge-Kutta 法,計(jì)算結(jié)果如圖2 所示.結(jié)果表明,如果計(jì)算程序輸入的參數(shù)組合經(jīng)過精細(xì)調(diào)整,打靶法能給出看似合理的解,然而這依賴于對(duì)T(0) 值和下游截?cái)辔恢脴O其謹(jǐn)慎的選擇和微調(diào),T(0) 稍有改變或計(jì)算域繼續(xù)向下游延伸就可能導(dǎo)致發(fā)散.具體到圖2 的算例,在大約x/λ1=12 (λ 表示分子平均自由程) 的位置之前,隨著計(jì)算的推進(jìn),各參數(shù)快速趨近于波后值,并在波后值附近保持了一段距離的“穩(wěn)定”,此時(shí)參數(shù)變化的趨勢(shì)以及參數(shù)分布曲線的形態(tài)是正常的,在該位置終止計(jì)算可以得到看似收斂的解.但如果繼續(xù)向下游積分,原本將要趨平的參數(shù)會(huì)快速偏離波后值,出現(xiàn)發(fā)散.

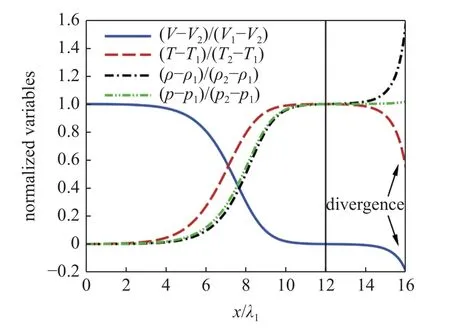
圖2 打靶法計(jì)算的單原子氣體激波結(jié)構(gòu) (Ma1=2)Fig.2 Profile of a Ma1=2 shock in a monoatomic gas calculated with the shooting method

合格的算法不應(yīng)過于依賴人工介入,然而在激波結(jié)構(gòu)問題中,打靶法很難像求解一般的兩點(diǎn)邊值問題那樣使用二分法、割線法之類的迭代方法自動(dòng)修正初值,因?yàn)榈? 步極其依賴人工判斷.此外,自動(dòng)修正T(0) 需要第3 步中有一個(gè)明確的截?cái)鄻?biāo)準(zhǔn),但實(shí)際上計(jì)算域的長(zhǎng)度很難確定,因?yàn)樵谟?jì)算中發(fā)現(xiàn),無論T(0) 如何接近其準(zhǔn)確值,只要向下游推進(jìn)足夠遠(yuǎn),發(fā)散總是不可避免;過短的計(jì)算域無法保證覆蓋整個(gè)激波結(jié)構(gòu),過長(zhǎng)的計(jì)算域則導(dǎo)致初值必須非常準(zhǔn)確才能保證收斂,因此對(duì)下游邊界的截?cái)嗪蚑(0)的迭代都依賴手動(dòng)操作.高度的敏感性暗示著不穩(wěn)定性的存在,需要在深入分析系統(tǒng)的動(dòng)力學(xué)性質(zhì)的基礎(chǔ)上提出改進(jìn)算法.

2.2 積分方向的重要性

激波內(nèi)任意位置氣體的狀態(tài)可以表示為相空間中的一個(gè)點(diǎn),那么激波壓縮過程可以表示為相空間中一條光滑軌線.分別記波前和波后狀態(tài)點(diǎn)為1 點(diǎn)和2 點(diǎn),求解激波結(jié)構(gòu)實(shí)際就是要找到一條連接1,2 兩點(diǎn)的積分曲線,將V-T相平面中這樣一條曲線叫做激波過程線 (即圖3 中的曲線S).已知上下游無窮遠(yuǎn)處速度和溫度梯度趨于0,即1,2 兩點(diǎn)使式 (12)～式(13) 的右側(cè)均為0,因此它們都是奇點(diǎn),激波過程線的斜率 dT/dV在這兩點(diǎn)處是 0/0 型未定式.

圖3 V-T 平面中的相軌跡Fig.3 Phase portrait in the V-T plane

約定x增加的方向/流動(dòng)方向/壓縮進(jìn)行的方向?yàn)榧げㄟ^程的正向.為了更直觀地了解系統(tǒng)的動(dòng)力學(xué)特性,根據(jù)式 (12)～式(13) 所確定的方向場(chǎng)/斜率場(chǎng),畫出V-T平面中的相軌跡圖,如圖3 所示,其中箭頭表示正向.相軌跡即圖中帶箭頭的實(shí)線,是隨著x的增加、相點(diǎn)的運(yùn)動(dòng)軌跡,每一條相軌跡都代表系統(tǒng)一個(gè)可能的解;相軌跡上每一點(diǎn)處的斜率與斜率場(chǎng)給定的一致,即相點(diǎn)的運(yùn)動(dòng)方向由方向場(chǎng)決定.相軌跡圖非常有用,它為微分方程建立了一種類似于流線圖的圖案,揭示了系統(tǒng)的定性性質(zhì),通過它可以對(duì)解的行為形成圖形化的認(rèn)識(shí).

從圖3 可以看出,1 點(diǎn)是不穩(wěn)定結(jié)點(diǎn),2 點(diǎn)是鞍點(diǎn),激波過程線S是從1 點(diǎn)發(fā)出并最終抵達(dá)2 點(diǎn)的異宿軌.在相平面中創(chuàng)建曲線M和N分別代表μ=0和 κ=0 情況下的激波過程線.在V-T相平面中,曲線M的方程可通過令式 (12) 右側(cè)中括號(hào)內(nèi)的項(xiàng)等于0 獲得;同理曲線N的方程也可通過令式 (13) 右側(cè)中括號(hào)內(nèi)的項(xiàng)等于0 獲得.由各自的曲線方程易知,M是拋物線;如果氣體是定比熱的,N也是拋物線.將M和N圍成的區(qū)域命名為L(zhǎng).文獻(xiàn) [39] 證明了 ρ-p圖中的激波過程線位于曲線M和N之間;類似地,很容易證明V-T圖中的激波過程線S也落在M和N之間,即區(qū)域L中.

如圖3 所示,從區(qū)域L內(nèi)任意一點(diǎn)出發(fā)進(jìn)行正向積分,除非該點(diǎn)嚴(yán)格位于所要求解的目標(biāo)軌線S上,否則相點(diǎn)會(huì)先靠近2 點(diǎn),但隨后又迅速遠(yuǎn)離,始終無法抵達(dá)2 點(diǎn),這也與圖2 算例發(fā)散的具體表現(xiàn)(流動(dòng)參數(shù)先趨近波后值,隨后又迅速偏離) 吻合.實(shí)際計(jì)算中,即使初值點(diǎn)剛好落在目標(biāo)軌線上,不可避免的舍入誤差也會(huì)導(dǎo)致積分曲線偏離目標(biāo)軌線,并被導(dǎo)出L區(qū)域.波后點(diǎn)是鞍點(diǎn),這是所有正向求解隨著數(shù)值積分向x=+∞ 推進(jìn)最終都會(huì)發(fā)散的根本原因.有理由認(rèn)為,所有包含正向推進(jìn)的激波結(jié)構(gòu)計(jì)算方法所獲得的“收斂”結(jié)果,都是在發(fā)散之前的“合適”位置強(qiáng)行終止計(jì)算所產(chǎn)生的假象,這種人為截?cái)嗉炔缓侠?也具有很大的隨意性.

3 逆向推進(jìn)計(jì)算方法

前已述及,正向推進(jìn)必然導(dǎo)致數(shù)值積分曲線偏離激波過程線、相點(diǎn)偏離2 點(diǎn).這個(gè)問題可用逆向推進(jìn)解決,即從區(qū)域L內(nèi)、2 點(diǎn)附近選擇一初值點(diǎn),從該點(diǎn)出發(fā)向上游積分至流動(dòng)參數(shù)幾乎不再變化為止.圖3 顯示逆向積分曲線必然匯聚于1 點(diǎn),所以該求解思路是可行的,但仍存在一個(gè)問題: 對(duì)初值不敏感固然是優(yōu)點(diǎn),卻也導(dǎo)致逆向求解無法與打靶法搭配使用,因?yàn)榇虬蟹康_定合適的初值,從而逼近精確解,而逆向求解會(huì)使初值誤差衰減、相點(diǎn)無限趨近于1 點(diǎn),無法為初值的修正提供反饋信息.因此需要一種新的初值確定方法.

3.1 基于L’H?pital 法則的初值確定方法

雖然2 點(diǎn)的參數(shù)無法直接作為初值使用,但如果已知激波過程線的終點(diǎn)斜率 (dT/dV)2,就能以較高的精度在2 點(diǎn)附近確定一初值點(diǎn) (V0,T0),其中V0的值由人為指定且略大于V2,T0可按Euler 格式給出

將式 (13) 和式 (12) 兩端分別相除,整理后得激波過程線在V-T圖中斜率的表達(dá)式

式 中JPm和JEm是常數(shù):JPm≡JP/Jm,JEm≡JE/Jm.注意理想氣體的比內(nèi)能u是且僅是溫度T的函數(shù),且du=cvdT,其中cv是定容比熱;μ 和 κ 一般也是溫度T的函數(shù).

2.2 節(jié)提到,1,2 兩點(diǎn)是奇點(diǎn),直接將波前或波后參數(shù)代入式 (16) 會(huì)使f/g成為 0/0 型未定式,給兩端點(diǎn)處激波過程線斜率的確定帶來困難,這個(gè)問題可用L’H?pital 法則解決.首先,激波過程線S位于曲線M和N之間,所以其端點(diǎn)斜率也介于M和N的端點(diǎn)斜率之間;又因?yàn)榍€M和N為或者近似為拋物線,它們的端點(diǎn)斜率為有限值,所以S的端點(diǎn)斜率存在且為有限值,進(jìn)而未定式f/g的極限也存在且為有限值,因此L’H?pital 法則適用.

將式 (16) 中的 ζ 乘到等號(hào)左邊,然后對(duì)等式兩端同時(shí)取極限——沿激波過程線向端點(diǎn)i(i=1,2)逼近,在這個(gè)過程中T可以視為V的函數(shù) (反之亦然).將f/g的分子分母同時(shí)對(duì)V求全導(dǎo),其極限的值保持不變

其中下標(biāo)V和T表示偏導(dǎo),fV=JPm-V,fT=cv,gV=2V-JPm,gT=R.值得一提的是,這里允許氣體是變比熱的,即不要求cv是常數(shù),它完全可以是T的函數(shù).

式 (20) 可整理成關(guān)于端點(diǎn)斜率 (dT/dV)i的一元二次方程

其具有一對(duì)相異實(shí)根

其中 γ 為比熱比,Pr為Prandtl 數(shù).不難看出這對(duì)根的符號(hào)相反.1 點(diǎn)是不穩(wěn)定結(jié)點(diǎn),有無數(shù)對(duì)積分曲線從該點(diǎn)發(fā)出,其中一對(duì)在1 點(diǎn)處的斜率取正根;包括激波過程線在內(nèi)的其他積分曲線在1 點(diǎn)處相切,斜率取負(fù)根.2 點(diǎn)是鞍點(diǎn),從該點(diǎn)發(fā)出和抵達(dá)該點(diǎn)的積分曲線各有一對(duì),兩個(gè)根分別為這兩對(duì)積分曲線在2 點(diǎn)處的斜率,其中負(fù)根是所需要的激波過程線的終點(diǎn)斜率.

3.2 一般求解程序

綜上,激波內(nèi)部結(jié)構(gòu)逆向求解的一般程序可總結(jié)為以下4 步:

(1) 根據(jù)波前參數(shù)計(jì)算出波后參數(shù),尤其是波后馬赫數(shù)Ma2、波后速度V2以及波后溫度T2;

(2) 將波后參數(shù)代入式 (22) 中負(fù)根的表達(dá)式,獲得激波過程線的終點(diǎn)斜率 (dT/dV)2;

(3) 選一略大于V2的速度值V0,將其與其他所需參數(shù)代入式 (15),計(jì)算出相應(yīng)的T0;

(4) 以 (V0,T0) 為初值點(diǎn),使用負(fù)步長(zhǎng) (即逆流向推進(jìn)) 對(duì)式(12)～式(13) 構(gòu)成的系統(tǒng)進(jìn)行數(shù)值積分;當(dāng)V與V1、T與T1的差值滿足精度要求時(shí)結(jié)束計(jì)算.

通過這4 步可獲得V和T的沿程分布,其他參數(shù)可基于它們進(jìn)一步計(jì)算獲得而無需參與數(shù)值積分,例如將V和T的值代入式(5) 和式(11) 可求出ρ和p的值.

為了在精度和效率之間取得最佳平衡,建議在激波結(jié)構(gòu)問題中使用變步長(zhǎng)的數(shù)值積分方法.這不僅是因?yàn)榧げê穸入S激波強(qiáng)度的變化很大 (從無限弱激波的無窮大厚度到強(qiáng)激波僅數(shù)倍分子平均自由程的厚度),還因?yàn)樗俣忍荻群蜏囟忍荻仍诩げ▋?nèi)部不同位置差異巨大.自適應(yīng)步長(zhǎng)可避免在參數(shù)變化劇烈的區(qū)域網(wǎng)格過疏或參數(shù)變化緩慢的地方網(wǎng)格過密.

3.3 算例驗(yàn)證

為驗(yàn)證逆向推進(jìn)法的有效性,對(duì)單原子氣體中Ma1=1.01～100的正激波進(jìn)行了求解,數(shù)值積分方法為步長(zhǎng)自適應(yīng)的4 級(jí)Runge-Kutta 法.不失一般性地,假設(shè)氣體是定比熱的,且其輸運(yùn)系數(shù)隨溫度的變化規(guī)律符合硬球分子模型的描述,即 μ 和κ 正比于T1/2.圖4 給出了代表性工況的沿程參數(shù)分布.

圖4 逆向推進(jìn)法計(jì)算的單原子氣體激波結(jié)構(gòu)Fig.4 Shock structures in a monatomic gas calculated with the backward marching method

圖4 中展示的流動(dòng)參數(shù)已經(jīng)過歸一化處理,x=0 的位置被統(tǒng)一規(guī)定在V=(V1+V2)/2 處,坐標(biāo)無量綱化所采用的分子平均自由程 λ 由硬球模型給定[1]

進(jìn)一步地,將打靶法 (shooting method,SM) 與逆向推進(jìn)法 (backward marching method,BMM) 計(jì)算的單原子氣體中Ma1=2 的正激波內(nèi)部的速度與溫度分布進(jìn)行了對(duì)比,如圖5 所示.

圖5 打靶法與逆向推進(jìn)法對(duì)激波結(jié)構(gòu)的計(jì)算結(jié)果的對(duì)比Fig.5 Comparison between the shock profiles calculated with the shooting method and the backward marching method

以上結(jié)果表明,逆向推進(jìn)法可以正確可靠地求解激波內(nèi)部流動(dòng)結(jié)構(gòu),明顯優(yōu)于打靶法.

4 結(jié)論

針對(duì)激波結(jié)構(gòu)問題,根據(jù)一維定常正激波控制方程的方向場(chǎng)畫出了激波內(nèi)部流動(dòng)的相軌跡圖,基于其拓?fù)浣Y(jié)構(gòu)分析了系統(tǒng)的動(dòng)力學(xué)性質(zhì),闡述了積分方向?qū)η蠼庠搯栴}的重要性,并指出在激波結(jié)構(gòu)問題中,采用正向推進(jìn)的傳統(tǒng)打靶法無法避免發(fā)散.為解決該問題,提出采用逆向推進(jìn)計(jì)算方法,并給出與之配合使用的初值確定方法.在非常寬的馬赫數(shù)范圍 (1.01～100) 內(nèi)測(cè)試了逆向推進(jìn)法,結(jié)果表明,該方法可以正確有效地求解激波結(jié)構(gòu)問題,且與傳統(tǒng)的打靶法相比,其具有以下優(yōu)勢(shì):

(1) 計(jì)算無條件收斂;

(2) 對(duì)數(shù)值計(jì)算中不可避免的初值誤差、舍入誤差等不敏感,且誤差隨著計(jì)算的進(jìn)行不斷降低;

(3) 無需對(duì)初值進(jìn)行迭代,積分一次即獲得最終解,計(jì)算量小.

應(yīng)當(dāng)指出,黏性應(yīng)力與熱流密度的表達(dá)式雖然會(huì)影響討論的定量細(xì)節(jié),但不會(huì)使激波系統(tǒng)內(nèi)在的定性性質(zhì)發(fā)生根本變化,因此本文的求解方法及主要結(jié)論的適用范圍不限于只具有線性本構(gòu)的經(jīng)典Navier-Stokes 方程.原則上,只要本構(gòu)關(guān)系不違背熱力學(xué)第二定律,即等效黏度和等效導(dǎo)熱系數(shù)在任意位置處都非負(fù),逆向推進(jìn)法可以向各種具有Navier-Stokes 形式守恒方程 (式(1)～式(3)) 的復(fù)雜流體系統(tǒng)推廣,如改進(jìn)的Navier-Stokes 方程、以Burnett 方程為代表的高階流體力學(xué)方程和Grad 矩方程等.對(duì)多原子氣體中考慮體積黏度或不透明氣體中考慮輻射傳熱的激波結(jié)構(gòu)問題,新方法亦適用.