關于絕對值和數軸的一個注

史寧中

關于絕對值和數軸的一個注

史寧中

（東北師范大學 數學與統計學院，吉林 長春 130024）

現行初中數學教材關于絕對值的內容，是通過線段長度或者距離定義絕對值，然后再論述有理數的絕對值性質，這樣的表述并不合適．絕對值概念源于復數大小的表達，然后用于向量長度的表達，因此，實數的和線段長度的絕對值表達都是特例，可以分別稱為絕對值的代數表達和幾何表達．兩種表達在形式上的一致性，構成了數形結合的理論基礎，成為初中數學的重要內容．建議：未來初中數學教材的編寫和教學，可以嘗試回歸絕對值的本原．

絕對值；數軸；復數；向量

至少對于數學教育而言，數形結合始于初中數學，是通過數軸和絕對值表述的．但仔細閱讀現行的教材可以發現，這些內容的表述不盡合理，不僅不能自圓其說，也沒有揭示數形結合的數學本質．正值《義務教育數學課程標準（2022年版）》實施之際，特寫此文供教材編寫者、教研員和中學數學教師參考，歡迎批評指正．

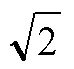
現在，關于絕對值概念的論述出現了矛盾：非負數的絕對值到底是線段長度呢？還是它本身所表達的數量的多少呢？因為在本質上，無論是正數還是負數都是對數量的抽象，數量相等、意義相反，而絕對值表達的正是相等的數量，因此才會有“相反數的絕對值相等”這樣的結論．事實上，這也是數學家定義絕對值的初衷．

因為在一般情況下，復數是無法比較大小的，于是德國數學家魏爾斯特拉斯于1841年發明了絕對值這個符號（參見：CAJORI F. A history of mathematical notations [M]. New York: Dover Publications, 1993: 123–124, 133．國內著作參見：徐品方，張紅．數學符號史[M]．北京：科學出版社，2006：269．），用以表示復數的大小：復數的實部與虛部平方和的開方．因此，對于實數的特殊情況，絕對值就是：非負數的絕對值是它本身，負數的絕對值是它的相反數．也就是說，任意實數的絕對值可以表示為

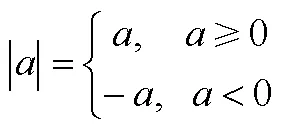
的形式．由此可見，最初定義的絕對值與數軸無關，可以稱為絕對值的代數表示．

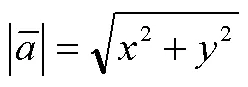
的形式．這恰好是數軸上的線段長度，可以稱為絕對值的幾何表示．

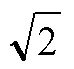
茍直線上之點，裂為前后兩段，前段各點均在后段各點之左，如是則必有一點，且僅有一點使此兩段之分裂得以產生．

是說，數軸上的點是連續的，基本特征是：任意一個點都可以把數軸上的點劃分為兩類，一類點在另一類點的左邊，這樣的劃分能并且只能產生一個點．類比數軸上的點，戴德金認為實數的連續性也具有這樣的特征：任何一個實數都對應一個劃分，可以把實數分為兩類，一類中的實數小于另一類中的實數，這樣的劃分能并且只能產生一個實數．借助連續性公理，戴德金最終定義了具有連續性的實數，使得極限的嚴謹定義與表達成為可能．

綜上所述，初中數學教材的內容最好既包括絕對值的幾何表示，也包括代數表示．數學教育應當讓學生知道，正是因為這兩種表示形式上的一致性，使得有理數與數軸上點的對應（小學數學的內容）升華到數量與距離的對應（初中數學的內容），幫助學生建立數形結合的直觀，感悟數學的本質．

A Note on Absolute Value and the Number Axis

SHI Ning-zhong

(School of Mathematics and Statistics, Northeast Normal University, Jilin Changchun 130024, China)

The content of absolute value in current middle school mathematics textbooks defines absolute value through segment length or distance, and then discusses the properties of absolute value for rational number, which is not an appropriate statement. The concept of absolute value originates from the expression of the magnitude of complex number, and later extends to the representation of vector lengths. Therefore, theabsolute value expressions of real numbers and segment lengths are both special cases, being termed algebraic and geometric expressions of absolute value, respectively. The formal consistency of these two expressions constitutes the theoretical foundation of the combination of numbers and shapes, becoming a pivotal aspect of middle school mathematics. This article suggests that the writing and teaching of future middle school mathematics textbooks should consider returning to the origin of absolute value.

absolute value; number axis; complex number; vector

G632

A

1004–9894（2023）05–0001–02

史寧中．關于絕對值和數軸的一個注[J]．數學教育學報，2023，32（5）：1-2．

2023–09–03

史寧中（1950—），男，江蘇南京人，教授，博士生導師，國家教材委員會數學專業委員會主任委員、中國教育學會學術委員會主任、高中數學課程標準修訂組組長、義務教育數學課程標準修訂組組長、CAP數學專家委員會主任，主要從事數理統計與數學教育研究．

[責任編校：周學智、陳漢君]