養殖網箱網綱和網衣水動力載荷研究

吳 皓,劉 強,范 為

(1 南方海洋科學與工程廣東省實驗室(湛江),廣東 湛江 524006;2 廣船國際有限公司,廣東 廣州 511400)

根據聯合國糧食和農業組織的數據統計,自20世紀80年代以來,水產養殖是過去40年來世界上增長最快的糧食生產方式,預計到2030年水產養殖將為人類提供超60%的魚類消費[1]。隨著水產養殖業不斷的投資升級,漁業養殖裝備從近海逐步走向深遠海,從傳統的養殖設施逐步向工業化漁業養殖裝備轉型升級。作為防止魚類逃逸的唯一屏障,漁網承擔著最為關鍵的角色[2]。

歷年來相關領域的學者和專家對網衣水動力進行了大量的理論和試驗研究。Xu等[3]闡述了3種網衣與流體相互作用的數值模擬方法,包括有限元法、計算流體力學(CFD)法以及有限元與CFD相結合的流固耦合法。有限元法涉及網衣的等效模型,包括三角單元模型、桿單元模型、質量彈簧模型以及集中質量模型[4-10]。CFD方法應用多孔介質模型模擬網衣,通過求解Navier-Stokes方程計算網衣水動力[11-14]。Cheng等[15]指出計算網衣水動力載荷的5種Morison模型和6種Screen模型。網衣Morison模型將網線和網結分別視為彼此獨立的圓柱形細長體和球體,網衣Screen模型則是將網衣看作是一系列子網片的集合。Magnus等[16]應用Morison模型和Screen模型對兩種典型的方形和圓形重力式網箱進行有限元計算,比較網箱在純流中的變形、養殖體積與拖曳力。曹宇等[17]應用Morison模型研究重力式網箱系統聯合浮式養殖平臺運動響應的受力分布及變形。苗玉基等[18]采用Screen模型模擬網衣在規則波作用下的波浪載荷,與水槽試驗結果吻合較好。

目前對網衣的研究大多關注柔性網箱網衣的受力和變形等,但關于網衣和綱繩耦合的研究還較少。深遠海養殖網箱一般由剛性框架和網綱網衣裝配而成的養殖網構成一個封閉的養殖空間。網綱一般由豎纖維繩或橫豎交錯布置的粗纖維繩連接到網箱周邊的剛性結構上,承擔著自身及網衣的載荷,能夠抵制網衣的過大變形從而有效維持養殖體積。

為研究此類網箱養殖網變形與網綱受力,提出一種結合Morison模型和Screen模型計算網綱和網衣水動力載荷以及網綱結構張力的有限元方法。該方法將網綱和網衣模擬成桿單元,通過建立網綱和網衣耦合的有限元模型,求解平衡內外力的控制微分方程組獲得耦合模型的張力和變形。通過研究網綱在純流及波流聯合作用下的張力和面法向偏移特性,為深遠海網箱工程的網綱網衣的選型與配合、強度校核及布置方案的優化等打下研究基礎。

1 網綱和網衣模型

本養殖裝備為可移動柱穩式養殖網箱,主要由浮箱、立柱、撐桿及養殖網等組成。養殖網由網衣和網綱構成,網衣目腳長度l為50 mm,網線直徑dw為3.5 mm,考慮海洋生物等附著的密實度Sn為0.176[19]。網綱直徑為22 mm,最小破斷力為3.88×103kN,動剛度為2.17×103kN/m。每面網衣均裝配在縱橫交錯分布的豎綱和橫綱上并與網綱縫合連接,初步方案的豎綱間距為1.3 m,橫綱間距為1.5 m。網衣和網綱的材質均為超高分子量聚乙烯纖維。圖1為網箱整網模型示意圖。

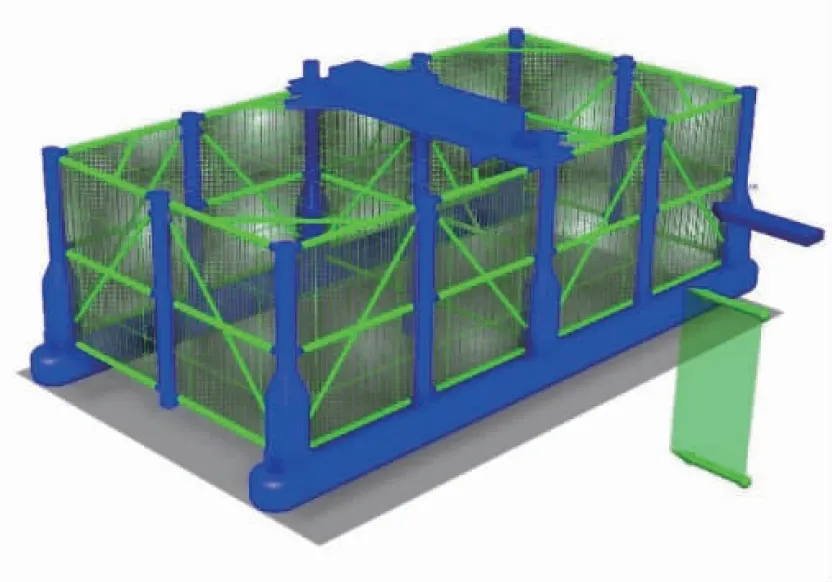
圖1 某可移動柱穩式養殖網箱的養殖網模型示意圖

2 計算方法

2.1 有限元模型

采用SIMA的RIFLEX非線性有限元求解程序對網綱和網衣相結合的耦合模型進行數值計算。耦合模型采用桿單元模擬網衣并基于Screen模型計算網衣水動力;采用Morison方程計算網綱水動力。從圖1可以看到,網箱由多面在結構尺寸等參數上相同的養殖網組成,取相鄰立柱間的養殖網為研究對象,構建養殖網網綱和網衣耦合的有限元模型。對象模型如圖2所示。

圖2 養殖網分析模型

固定邊界為左右兩邊的立柱和上中下的橫撐,中間的橫撐將養殖網分隔成上下獨立的養殖網A和B。模型中垂向和橫向的網綱等構件分別以“V”和“H”加編號予以表示。有限元模型應用桿單元對網綱和網衣進行等效模擬,并通過桿端節點共用的方式將網綱和網衣模型耦合,可進行時域耦合計算,見圖3。

圖3 養殖網網綱和網衣耦合的有限元模型

桿單元為連接兩端節點的線單元,可用于計算軸向拉伸變形,但不發生彎曲和扭轉變形[20]。其軸向張力為:

(1)

式中:N為單元軸向力;L為拉伸變形后的長度;L0為初始長度;E為彈性模量;A為橫截面積。

對網綱和網衣耦合的有限元模型,時域計算的非線性動態平衡微分方程組為:

(2)

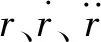
2.2 水動力模型

2.2.1 網衣水動力模型

Kristiansen等[4]將計算網衣受力的水動力模型分成兩類,分別是Morison模型和Screen模型。網衣水動力可以表述為下式。

(3)

式中:ρ為水密度;▽為網衣浸水體積;Anet為網衣投影面積;u為流體速度;v為結構速度;經驗水動力系數Ca和Cd分別為附加質量力系數和拖曳力系數,其取值取決于試驗數據,與庫卡數、雷諾數、網線粗糙度以及網衣密實度密切相關[4]。上述等式右邊多項式前3項依次為入射力(或稱Froud-Krylov力)、繞射力及輻射力,統稱為慣性力;最后一項為粘性力。大量試驗結果表明,網衣慣性力約為粘性力的dw/H倍(H為波高)[21]。例如,當dw=1 mm,H=1 m時,慣性力約為粘性力的0.1%。故網衣慣性力遠小于粘性力,計算中可忽略不計。

網衣水動力既取決于實際的流速,也取決于網衣自身的水動力特性。水動力特性與網衣材料(金屬或纖維)、網目形狀(方形或菱形)、網目大小、網線直徑、網線編織方法(捻線或編織線)以及網衣編織方法(無結或有結網)有關。光滑銅網在穩流中的阻力明顯低于粗糙的尼龍網[22]。同環境條件下有結網的阻力比無結網的阻力要高約10%[23]。大量試驗結果表明,網衣的水動力特性主要依賴于兩個無因次變量,密實度Sn和雷諾數Re[22-25]。其中理想方形網的水動力主要取決于Sn。

Sn是網衣凈投影面積與輪廓投影面積的比值。理想的無結方形網(見圖4)Sn計算公式為:

圖4 養殖網網衣示意圖

(4)

式中:dw為網線直徑,lD為相鄰網線中心距。

Re與網衣的網線直徑和流體速度有關。

(5)

式中:U為未受擾動的流體速度;v為流體運動粘性系數。網衣Re的典型范圍通常為(100,10 000)。

Screen Model模型將網衣分解為一系列子網片,每一網片的受力可分解為沿網片法向和切向的兩個分力或者水平拖曳力和垂向升力的兩個分力,見圖5。流體與網片相對速度Urel為:

圖5 養殖網網衣受力示意圖

Urel=γU∞+uw-us

(6)

式中:Urel為相對速度,U∞為流速,uw為水質點速度,us為結構速度。γ=1代表前方的網衣,γ=r代表后方的網衣,r為流速的折減系數。

網衣水動力FH為拖曳力FD和升力FL的兩個矢量分力之和。

(7)

(8)

式中:ρw為流體密度,At為網片面積;Urel為相對速度;Cd和Cl分別為拖曳力系數和升力系數;id和il分別表示拖曳力和升力的單位矢量。Cd和Cl由試驗得到,主要與Re、Sn及入射角θ有關。其中θ為波流入射方向與網片法向的夾角。本研究的Cd和Cl基于L?land提出的Screen模型計算,其適用密實度范圍為(0.13,0.35)[26]。

CD(Sn,θ)=0.04+(-0.04+0.33Sn+

(9)

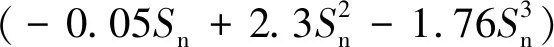
sin2θ

(10)

L?land公式并不包含雷諾數,Cd和Cl不隨雷諾數而變化。一般來說,Cd和Cl高度依賴于Sn,并且當Re范圍為(100,10 000)時,Re對網線阻力系數的變化幾無影響,可忽略[15]。Cd和Cl隨Sn的增加而增大,說明在其他條件相同的情況下,網衣Sn越大,Fh越大。L?land提出的Screen模型的Cd隨θ的增大而衰減,并遵循余弦函數曲線的規律。Cl的變化遵循正弦函數sin2θ曲線的變化規律。當θ為零時,升力為零;當θ較小時(θ<30°),升力相對于拖曳力是小量,后者起主導作用。

2.2.2 網綱水動力模型

網綱水動力的計算基于Morison模型[27]。網綱由豎綱和橫綱交錯布置,網目尺寸相對于網綱直徑要大得多,Sn對網綱阻力影響很小,所以適合采用Morison方程計算網綱水動力。

(11)

式中:dRope為網綱直徑;LRope為網綱長度;ARope為橫向截面面積;Cd和CA分別為拖曳力系數和附加質量力系數。在大多數情況下,拖曳力系數主要是Re的函數。式中的拖曳力項可分解為兩部分:垂向拖曳力Fn和軸向拖曳力Fτ,見圖6。

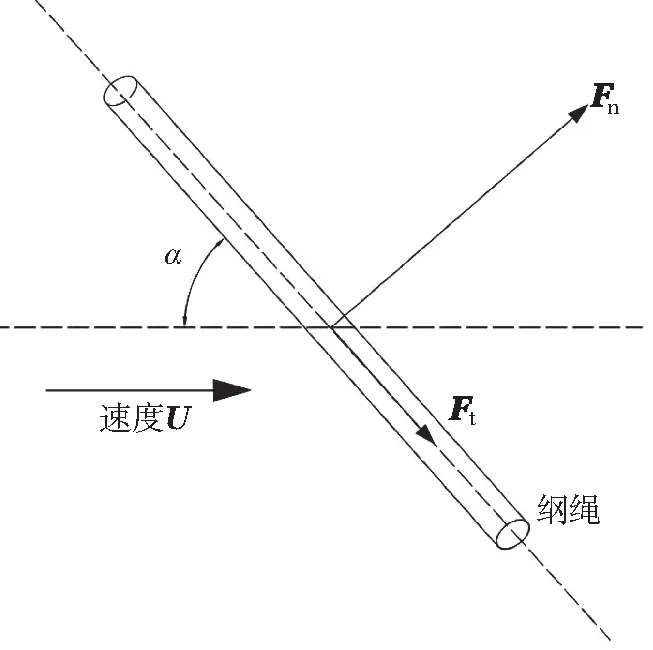
圖6 養殖網網綱受力示意圖

(12)

(13)

式中:un和uτ分別為垂向和軸向流體相對結構的速度矢量;Cn和Cτ為垂向和軸向拖曳力系數。一般來說,Cτ比Cn要小得多,因此忽略不計軸向拖曳力的模擬結果是可以接受的。

2.3 尾流

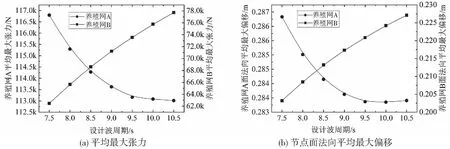
來流經過網衣后將產生尾流效應。由于流體的粘性作用將使尾流發生擾動,流速受到折減[28],下游網衣的受力也將有所減小,一般采用速度折減系數r(0

Udownstream=rUupstream

(14)

式中:Uupstream為來流速度,Udownstream為尾流速度。折減系數r一般為Re,Sn及θ的函數,在實踐中較常用的計算公式為r=1-0.46Cd,Cd為Screen模型中網衣的拖曳力系數。

3 結果與討論

3.1 純流條件下的張力與面法向偏移

網箱坐底吃水d為23.4 m,自存環境條件為:有義波高5 m,流速1.6 m/s。采用確定性的設計波方法,設計波波高H為有義波高的1.9倍,設計波周期范圍為7.5～10.5 s,Ursell數最大值約為21.9,適用Stokes 5階波波浪理論[29]。為研究本養殖網的網綱最大張力與面法向偏移,假定純流、波流的入射角為0°。

純流條件下當流速為1.6 m/s時,對養殖網A網綱單元的最大張力值進行統計,作垂線圖如圖7所示。

圖7 養殖網A在純流1.6 m/s下的最大張力響應統計圖

可以看到,豎綱和橫綱的最大張力都呈現中間高、兩邊低的走勢,與應用多孔介質模型研究的網衣整體呈現中間受力大的特性相同[30]。由于豎綱的長度要小于橫綱,相對伸長率大于橫綱,故從圖中可以看到豎綱的最大張力整體要大于橫綱。統計養殖網A和B網綱單元的最大張力和節點面法向最大偏移并取平均值作圖如圖8所示。

圖8 養殖網A和B隨流速的平均最大張力和節點面法向平均最大偏移

圖8a表明,隨著流速的增加,平均最大張力與面法向最大偏移弱非線性增大。該特性類同于Magnus等[16]指出網箱阻力隨流速的增加呈非線性增加的趨勢。圖8b表明,隨著流速增加,網綱承力逐漸增加,拉伸變形也逐漸增大,這與對柔性網衣變形的有關研究得出的隨流速增加而增大的特性一致[31]。由于養殖網A部分位于水面以上,圖中可以看到A的平均最大張力與面法向最大偏移整體稍低于B。

3.2 波流聯合作用下的張力與面法向偏移

取T=7.5 s的波流工況,統計養殖網A的網綱單元最大張力并作圖9。垂線圖表明豎綱和橫綱最大張力整體都呈現中間高,兩邊低的走勢。同一豎綱或橫綱網綱單元沿軸向的最大張力呈現末端高,中間低的走勢。由于養殖網A整體水深比B要淺,設計波波速更大,養殖網A網綱單元的最大張力統計值約為188 kN,比B大約88%,這種顯著性差異說明當養殖網B采用與A同規格的網綱時其間距可相對布置的更寬。Qu等[32]對柔性網箱的研究同樣表明水深的顯著作用,體積剩余率隨著水深增加而增加,單位體積的阻力變小。

圖9 養殖網A流速1.6 m/s、波幅4.75 m、周期為7.5 s的最大張力響應統計圖

通過箱線圖10對周期T=7.5～10.5 s下的網綱單元最大張力進行統計性分析發現,養殖網A網綱單元最大張力的統計最大值、中位值和均值隨著周期的增大呈現緩慢減小的趨勢。箱體寬度變化不大,說明整體網綱單元最大張力的波動程度相當。養殖網B的統計最小值、最大值、中位值和均值隨著周期的增大緩慢遞增,與A走勢相反。

圖10 養殖網在流速1.6 m/s、波幅4.75 m下的最大張力統計性分析

這種不同走勢的原因在于流速在不同水深處隨周期變化的差異性。

從圖11可以看到在自由液面附近,流速隨設計波周期增大而減小;不同周期的設計波流速均隨水深的增加而減小,但程度不同。周期越小,流速隨水深的增加衰減越快。養殖網B所處水深的流速隨周期增大而增加,故其最大張力隨著周期的增加而增加。總體上,在設計波周期范圍內的養殖網A網綱單元最大張力的統計最大值顯著大于B。

圖11 不同周期波速與水深的變化關系

圖12表明了養殖網A和B的網綱單元平均最大張力和面法向平均最大偏移隨設計波周期的變化。可以看到養殖網A的均值隨周期的遞增而向下凹;B則呈向上微凸的走勢。

圖12 養殖網A和B網綱單元平均最大張力和面法向平均最大偏移隨周期的變化

4 結論

提出一種結合計算Morison模型和Screen模型的有限元方法,網衣水動力的計算基于Screen模型,網綱水動力的計算基于Morison模型。通過建立網綱和網衣耦合的有限元模型,研究了有限元模型在純流、波流聯合作用下的張力與面法向偏移。對數值計算結果進行統計分析發現:純流條件下養殖網A和B的網綱單元最大張力和節點面法向最大偏移的統計最小值、最大值、中位值和均值均隨著流速的增加而遞增,均值隨流速的變化曲線呈弱非線性增加;波流聯合作用下養殖網A和B的所有網綱單元最大張力和節點面法向最大偏移的統計特征存在顯著差異,同等條件下A的網綱統計最大張力和平均最大張力均比B要大的多,水深的明顯作用說明B的網綱間距可相對A布置的更大一些。A的網綱平均最大張力和節點面法向平均最大偏移隨設計波周期的增加而非線性遞減,B則呈現弱非線性遞增的走勢。通過網衣網綱的耦合分析方法以及張力與偏移的特性分析,將指導網衣網綱的選型、裝配與布置設計得更加合理。例如,由2片獨立養殖網分成4塊甚至6塊等,可有效減小張力與偏移;水深相對更深的養殖網網綱間距可相對布置得更大;單片養殖網網綱可布置成從中間向兩邊由密向疏等等,這都將對方案設計階段的設計和優化具有重要的指導意義。