多圓柱繞流的數值模擬及力學分析

趙紅曉

（同濟大學航空航天與力學學院，上海 200092）

0 引言

圓柱的繞流現象在工程中廣泛存在，如管排［1-2］、橋墩［3-4］、電纜和高聳建筑［5］等結構周圍的流動問題。1940 年11 月7 日，美國華盛頓州塔克馬海峽大橋因風振致毀，事故原因正是空氣繞流形成的卡門渦街引起的橋梁共振。作為典型鈍體的一種，近代學者對圓柱繞流的研究一直沒有停息過。

1911 年，馮·卡門觀察到在一定條件下的定常來流繞過某些物體時，物體兩側會周期性地脫落出旋轉方向相反、并排列成有規則的雙列線渦，并對渦街的誘導速度、穩定性和阻力等做了分析［6］。Coutanceau等［7］揭示了圓柱后尾流形態和雷諾數之間的對應關系。Zdravkovich［8］研究了雙圓柱串列在流體流動速度很小時，不同的間距比L/D（圓柱間距與圓柱直徑之比）對兩柱間隙中的速度分布和下游柱尾流場中的速度分布具有明顯影響。Le 等［9］發現雙圓柱繞流在間距比L/D=2 時尾流產生的渦街迅速消失，間距比為4.5 時兩條尾流的形狀隨時間隨機發生變化，出現渦脫落方向相同、相反等4 種典型的尾流形狀。Yokoi等［10］研究了雙柱并列（非等直徑），間距比為0.25 ～1.5 之間時流體形態發生交替偏斜，間距比大于1.5時，兩柱后分別形成各自的渦脫落。張愛社等［11］利用有限元法對等邊三角形布置的等直徑3 圓柱繞流問題進行了研究，表明小圓柱的位置、大小、個數以及雷諾數變化等對主圓柱有影響。Kuo 等［12］研究了2 個并列小圓柱置入尾流區，可有效地抑制渦街的產生，并使主圓柱的升力系數降低了70% ～80%，壓力、阻力減小也很明顯。張洪軍等［13］研究了附屬小圓柱對并列雙圓柱尾流流場的影響。Muddada 等［14］研究了放置于主圓柱后的旋轉小圓柱可以有效地抑制渦街的生成。

由于流動的復雜性，目前以多圓柱群為對象的研究相對較少，工程情況中圓柱以圓柱群的形式出現的案例卻十分常見，本文選取不等直徑多圓柱群實驗裝置進行仿真研究。

1 數值模擬

1.1 控制方程

本文采用Fluent軟件進行數值模擬，選用Simplec算法（半隱式方法Semi-Implicit Method for Pressure Linked Equations）進行計算。本文研究中，低雷諾數下水的流動，可近似為不可壓縮流體，則二維連續性方程可簡化為：

動量方程為動量守恒定律在流體力學中的表示形式：

式中：u、v、w為3 個速度分量；p為壓強；ρ為流體密度；μ為流體動力黏度。

升力系數Cl和阻力系數Cd是流體力學中的無因次量，用來表示物體在流體中的升力和阻力大小

式中：Fl、Fd分別為物體受到的升力和阻力；v∞為無限遠場的來流速度；S為物體在來流方向上的投影面積。

雷諾數

式中，v、L分別為流場的特征速度和特征長度。雷諾數物理上表示慣性力和黏性力量級的比。

本文均設置左側邊界為速度入口，右側邊界為壓力出口，遠場壁面為對稱邊界條件，圓柱壁面采用無滑移壁面。流體介質為水，密度ρ=1000 kg/m3，動力黏度μ=1.0 ×10-3kg/（m·s）。

1.2 計算模型

多圓柱繞流研究實驗裝置如圖1 所示，以還原實驗裝置中的流動規律，劃分模型進行多組仿真計算。

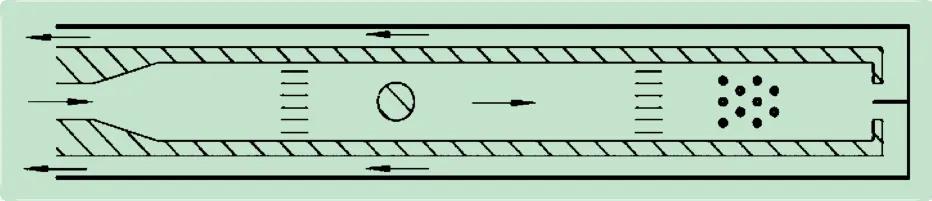
圖1 流態演示裝置斷面示意圖

為避免過于龐大的模型造成不必要的計算時間浪費，需對模型進行適當的簡化和劃分。

如圖2 所示，模型保留了實驗裝置中近壁面繞流和多圓柱群繞流的流域，并在入口和出口處做了適當的加長。與實驗室現象進行對比，觀察能否正確模擬實際流動，保留了實驗裝置中的柵格，多圓柱排列方式、尺寸和編號如圖3 所示。

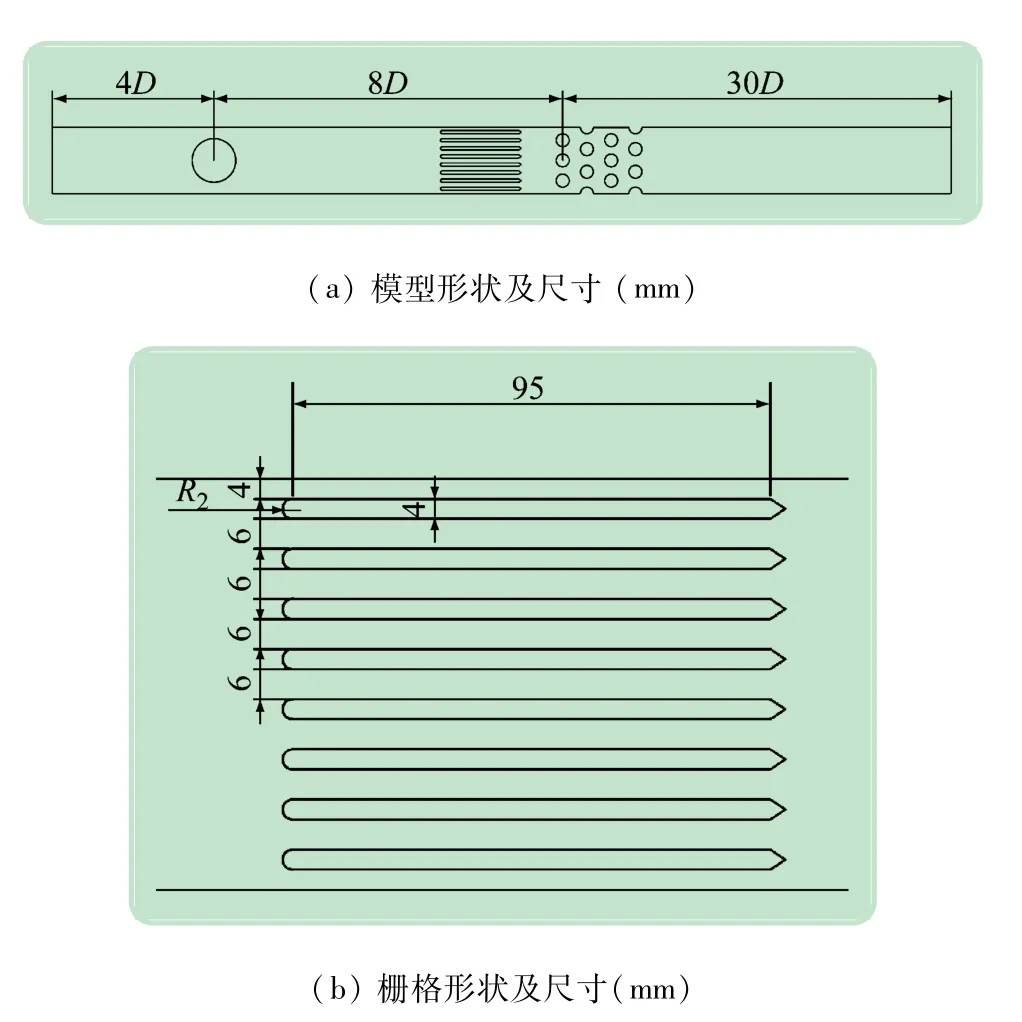
圖2 實驗裝置物理模型及尺寸

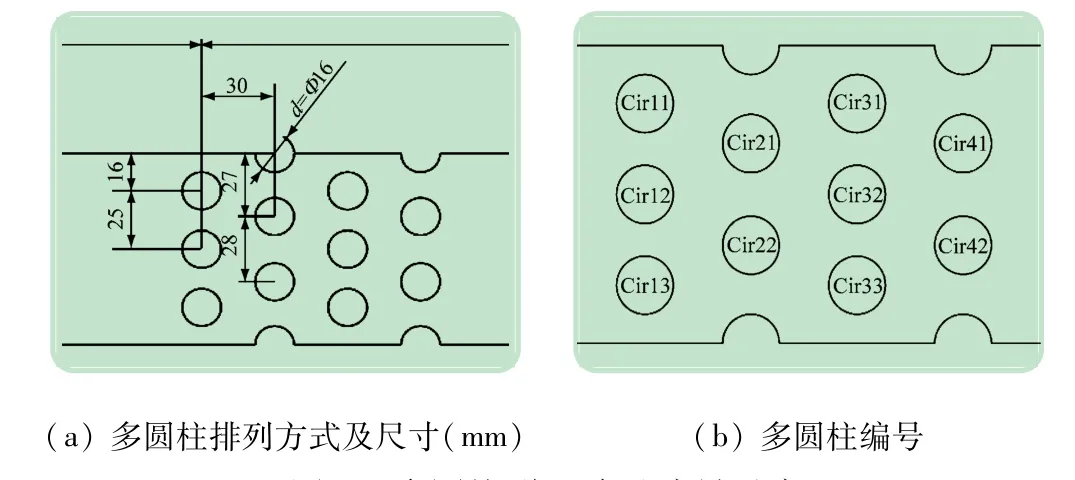
圖3 多圓柱群尺寸及編號示意

1.3 網格劃分及計算方法驗證

采用結構化網格的方法進行網格劃分，建立oblock與圓柱面以及柵格前緣、尾緣的圓角關聯，將其余邊與壁面和柵格長邊關聯，并在湍流情況中，運用式（7）估算第1 層網格到柱面的距離Δy進行相應加密。最終得到的網格具有較好的質量和長寬比，網格劃分如圖4 所示。

圖4 實驗裝置網格劃分

網格劃分與層流驗證模型時相同。為保證圓柱面上第1 層網格滿足y+≈1，估算確定第1 層網格到柱面的距離［15］

代入特征長度L=D=0.01 m，Re=3900，得到Δy=0.03 mm，加密后網格如圖5 所示。

圖5 圓柱周圍及局部網格加密圖

2 層流模型和紊流模型驗證

參考文獻［16］，使用相同的物理模型進行層流驗證。左側為速度入口，右側為壓力出口，遠場壁面為對稱邊界條件，圓柱壁面采用無滑移壁面。計算區域20D×25D，采用結構化網格，計算參數見表1，計算結果見表2。

表1 層流驗證模型仿真參數

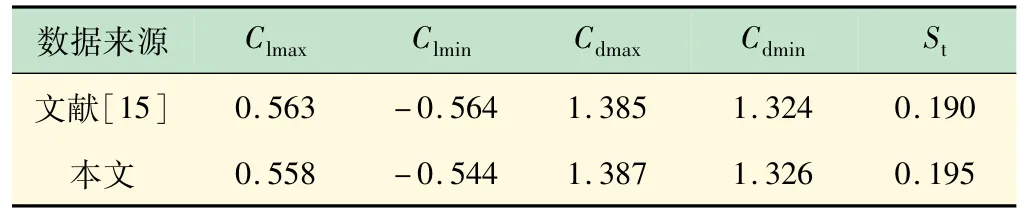
表2 層流模型驗證結果與文獻數據對比

由表2 可知，計算結果與文獻［15］基本一致，可使用層流模型對小雷諾數的情況進行模擬。

參考文獻［15］中使用相同的物理模型進行紊流驗證。左側為速度入口，右側為壓力出口，遠場壁面為對稱邊界條件，圓柱壁面采用無滑移壁面。計算區域20D×40D，靠近圓柱加密網格，采用結構化網格，計算參數見表3，計算結果見表4。

表3 湍流驗證模型仿真參數

表4 湍流模型驗證結果與文獻數據對比

計算結果與文獻［15］基本一致，可使用分離渦模型進行模擬。

3 仿真計算

分別采用以上驗證計算模型和劃分網格的方法分別對多圓柱繞流模型（見圖3（a））進行數值模擬，表5中雷諾數均為小圓柱雷諾數，參數設置見表5。

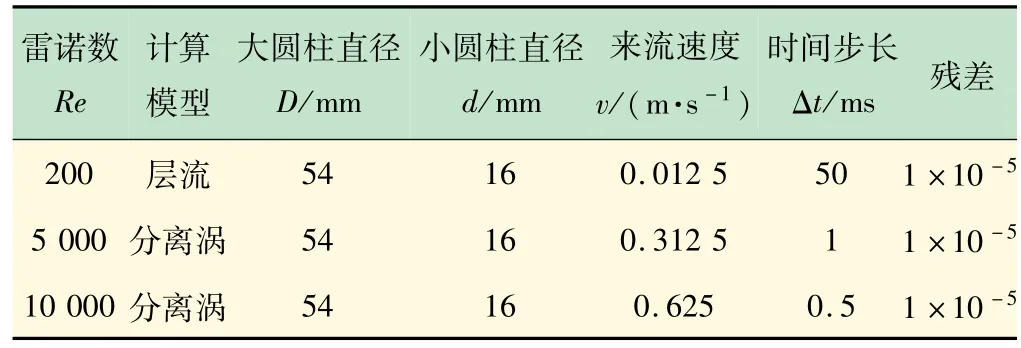
表5 實驗裝置中多圓柱繞流仿真參數

由速度云圖圖6（a）可見，在Re=200 時，以大圓柱的前緣為中心，水流在駐點受阻后，被迫向兩邊流動，在靠近圓柱尾部的邊界上，主流開始與圓柱體分離，邊界層分離后，在分離區的下游形成回流區，即為尾渦區。后流經柵格區域，在流經柵格的各狹縫中，由于截面積的減少，流動皆有一定的加速。流體流經多列小圓柱時，列與列之間的尾渦出現摻混而紊動更強烈，渦的長度由于受到限制變短。第4 列圓柱則直接在后方產交替脫落渦。

由圖6（b）速度云圖可見，當Re=5000 時，大圓柱尾渦出現明顯的兩列渦，且脫落形成長度明顯變短，渦街的寬度變窄，尾流呈復雜的湍流特征渦。小圓柱的第1 列圓柱限制了后面第2、3 列圓柱分離剪切層的卷起，使其不能產生強烈的旋渦脫落，第3、4 列圓柱的渦在后方混合，形成更為復雜的尾流。各圓柱后方仍有一定范圍的回流泡，旋渦脫落現象在下游第4 列圓柱后尾渦脫落成偏斜的尾流模式，隨著雷諾數的增大，第4 列后的紊動就越強烈。

當Re=10000 時，從圖6（c）的速度云圖可觀察到其流動與Re=5000 時十分相似，但紊動更強烈，尾流模式和圓柱受力不具有周期性，是由于尾渦區的長度和紊動強度與來流的雷諾數有關，雷諾數越大，紊動越強烈。

當Re=200 時，由圖7（a）、（b）可見，大圓柱受到最大阻力系數最大，小圓柱中第1 列（從左向右看）圓柱阻力次之，第3 列圓柱所受阻力略小于第1 列圓柱，位于中心線上的圓柱12、32 仍相比同列受到更大的阻力。第2 和第4 列圓柱所受阻力比第3 列略小，第4列圓柱所受阻力略大于第2 列。第4 列圓柱升阻力系數的振幅比前幾列大。

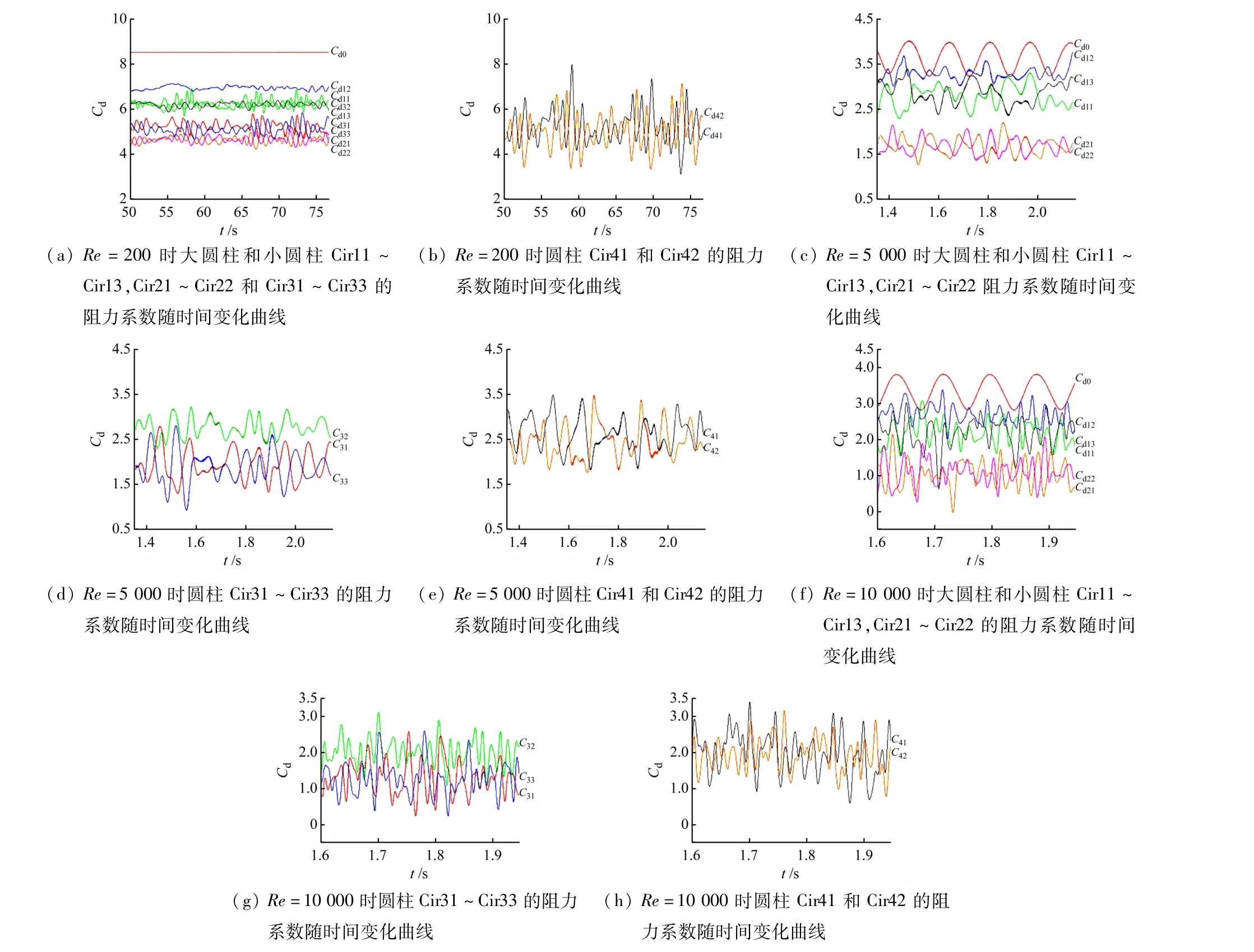
圖7 多圓柱繞流阻力系數隨時間變化曲線

當Re=5000 時，由圖7（c）、（d）和（e）可見，大圓柱的最大阻力系數仍是最大，但比Re=200 時小。圓柱12 阻力系數次之，第4 列圓柱的阻力系數比第3 列大，位于中心線上的圓柱12、32 仍相比同列其他圓柱受到更大的阻力，各圓柱的阻力系數均有一定幅度的振蕩，后方的圓柱較前方有更大的振蕩幅度。

當Re=10000 時，由圖7（c）、（d）和（e）可見，各圓柱的阻力系數均有一定幅度的下降和振蕩，后方的圓柱較前方有更大的振蕩幅度。同樣位于中心線上的圓柱12、32 仍相比同列受到更大的阻力。

由圖7 中不同雷諾數下的阻力系數可見，大圓柱的升力系隨著雷諾數的增加而降低，小圓柱的繞流阻力系數總體上也隨著雷諾數的增加而降低，隨著雷諾數的增加，流動由層流變為紊流，湍動更強烈，各阻力系數均隨時間產生微小振蕩，振幅逐列增加。

當Re=200 時，由圖8（a）～（d）可見，第4 列小圓柱升力系數大約在±4.5 這一范圍內振蕩，其次是圓柱31、33，圓柱11、13。圓柱21、22 升力系數在零上下振蕩，對稱軸上的大圓柱和小兩圓柱12、32 所受升力為零。第1、3 列和第2、4 列同側圓柱所受升力仍具反向性。

圖8 多圓柱繞流升力系數隨時間變化曲線

當Re=5000 時，由圖8（e）～（h）可見，升力系數的振蕩幅度也逐列增加，第4 列圓柱的升力系數振幅較大，最大值為其他圓柱的2 倍以上，第3 列升力系數次之，第1 列最小。不過前2 列圓柱的振蕩較小，除去中心線上的圓柱12、32，其他圓柱受力方向也沒發生改變，而大圓柱和小圓柱第4 列圓柱隨著尾流的復雜化，其升力系數開始較大幅度的振蕩，且方向會隨時間改變，說明紊動強度增加，能量損失更大。

當Re=10000 時，由圖8（i）～（l）可見，規律和雷諾數5000 時相似，升力系數的振蕩幅度較之雷諾數5000 時更大，流體紊動強度繼續增加。

對比Re=5000 時的速度云圖和實驗裝置的流動圖像（見圖9），可發現兩者較好符合，認為仿真結果與實際流動是很接近的，可用數值模擬的方法替代實驗裝置來演示紊流的流態。

圖9 實驗裝置流動圖像對比

4 結語

本文對實驗裝置簡化模型在3 種雷諾數下進行了數值計算和流態、阻力系數和升力系數分析，可知，多圓柱繞流在雷諾數Re=5000 時的速度云圖和實驗裝置的流動圖像符合，認為仿真結果與實際流動是很接近的，可采用模擬的方法去演示流體的紊動機理，為流體力學虛擬仿真開發提供有益的探索。