基于VGG-19 和卡爾曼預處理的WSNs測距方法*

劉超敏，胡玉平

（1.鄭州財經學院 信息工程學院，河南 鄭州 450000；2.廣東財經大學 信息學院，廣東 廣州 510320）

0 引 言

基于無線傳感器網絡（wireless sensor networks，WSNs）［1］的測距和定位技術在環境監測等領域得到了廣泛的應用。對于測距技術來說，針對無線傳感器包含的網絡節點間存在的距離進行檢測時使用最為普遍的方式為接收信號強度指示（received signal strength indication，RSSI）［2］。從WSNs測距技術的角度出發，其最核心的目的為針對未知節點所對應的信號完成傳輸過程，進一步轉移至錨點以及錨節點組。這些錨節點或遠程計算機根據錨節點接收到的無線信號強度，計算未知節點到錨節點組的距離［3，4］。當基于RSSI測距的未知節點進行定位時，距離測量的精度將直接影響節點位置計算的精度［5］。

傳統的測距方法包括對數正態陰影模型（log-normal shadowing model，LNSM）、LNSM 校準的自適應神經模糊推理系統以及反向傳播（back propagation，BP）神經網絡測距模型等［6，7］。基于LNSM 估計是在理想環境的假設基礎上進行的。由于最小二乘（least square，LS）法計算未知節點位置時的受測距誤差較大，文獻［8］提出一種改進花授粉算法的RSSI定位方法易受環境因素影響。文獻［9］使用LNSM進行原始估計，基于自適應［10］神經模糊推理系統的智能技術可提高距離估計的準確性，尤其在室內環境中減小了無線多徑損傷對信號質量的嚴重影響。基于BP神經網絡的測距模型是將RSSI值用作模型的輸入，將距離信息用作模型的輸出，并通過訓練當前環境中收集的數據來使模型適合當前環境中RSSI 與距離之間的關系［11］。文獻［12］提出了一種基于深度卷積神經網絡（deep convolutional neural network，DCNN）的測距模型，自動提取在不同地面環境中信號傳播的高級語義特征。文獻［13］基于BP神經網絡模型，引入蟻群優化（ant colony optimizaton，ACO）算法進行優化，尋找最優初始閾值和權值。文獻［14］提出了一種基于BP 神經網絡的RSSI 測距方法，有效減少了RSSI測距誤差。但過多的神經元會增加訓練時間，會使網絡的泛化能力和預測能力減弱，神經元太少會影響后續值與前體值的關系［15］。雖然BP神經網絡測距模型和自適應神經模糊推理系統可以很好地提取當前環境下的信號傳播特性，但由于不同環境中信號衰減特性不同［16］。

本文提出了一種基于視覺幾何組（visual geometry group，VGG）—19 和卡爾曼預處理的WSNs 測距方法，可以根據圖像數據和RSSI數據自動提取不同地面環境的信號傳播特性，在不同的地面環境中實現準確的距離估計。

1 VGG-19 網絡模型

1.1 VGG—19 的網絡拓撲結構

VGG—19網絡的拓撲結構如圖1所示［17］。其中一段卷積內含有的卷積層數目累計為2～3 個，同時卷積核對應的尺寸為3 ×3，步長為1。

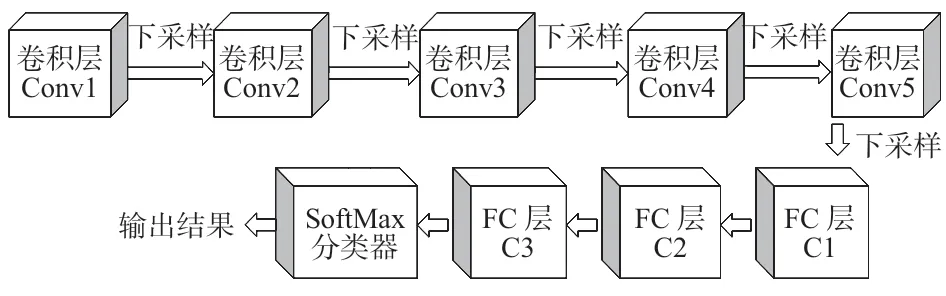
圖1 VGG-19 網絡的結構

網絡中的下采樣層采用最大池化（Maxpooling），激活函數采用修正線性單元（rectified linear unit，ReLU）。全連接（fully connected，FC）層的節點數依次是2048，2048，500。除此之外，VGG—19 網絡所對應的輸入圖像尺寸為224 ×224。

1.2 卷積層和激活函數

這里擬定網絡內部第l層的第j個特征圖表示如下

1.3 下采樣層和FC層

VGG—19網絡［19］內部的下采樣層選擇的是Maxpooling，數學形式如下

1.4 損失函數

使用均方誤差（mean square error，MSE）損失函數計算損失，L（θ）計算如下

式中 I（i）為輸入的圖像數據；R（i）為輸入的RSSI值；d（i）為測量獲得的距離值。通過最小化損失函數進行測距網絡的優化。

2 基于VGG-19 的WSNs測距模型

2.1 整體架構

所提模型的整體架構如圖2所示。

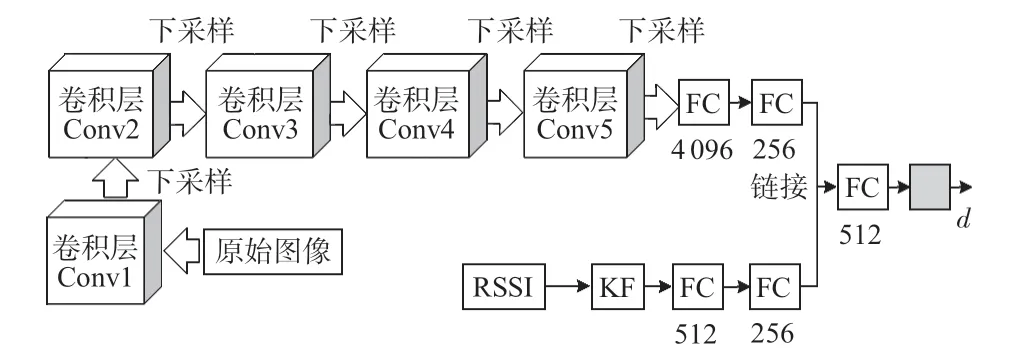
圖2 所提模型的整體架構

所提網絡模型有2 個輸入分支，其中一個分支的輸入是來自相機的固定尺寸，224 ×224 的地面圖像，該分支包含5 個卷積層，表示為Conv1～Conv5，5 個下采樣層（Maxpooling層）和3個FC 層。另一個分支的輸入是接收器獲得的RSSI值，該分支包含1 個KF器和3 個FC層。然后，將2個分支的輸出發送到FC層，基于這些輸出值，可以提取信號在不同環境中的傳播特性，最終輸出的是WSNs 中的距離估計。如果網絡中有太多層或隱藏的神經元，則模型的訓練時間將增加，但如果層數太少，則模型的訓練可能效果不佳。通過對樣本大小的分析和實際驗證，所提網絡模型的參數配置如表1所示，卷積層參數表示為“Conv（感受野大小）-（通道數）”。

表1 網絡模型的參數配置

所提網絡是一個端到端系統，可以自動提取不同地面環境的信號傳播特性。使用地面圖像數據和RSSI 數據作為網絡的輸入，通過網絡計算數據后，將獲得一個預測結果，即距離估計，它對應于在地面環境中接收到的RSSI值。通過將距離估計值與米尺的真實值進行比較，可以計算出每一層的BP誤差，并根據誤差調整每一層的參數，直到模型收斂為止。

2.2 基于KF的RSSI數據處理

通過圖3能夠得出，在完成KF處理的過程后，RSSI數據的波動性［20］出現了明顯的下降，其RSSI 值主要在［-60，-58］dBm范圍內波動，而原始數據在［-64，-56］dBm范圍內波動。由此，表明KF能夠有效優化以RSSI 為核心的測距算法所具有的穩定性以及精度。

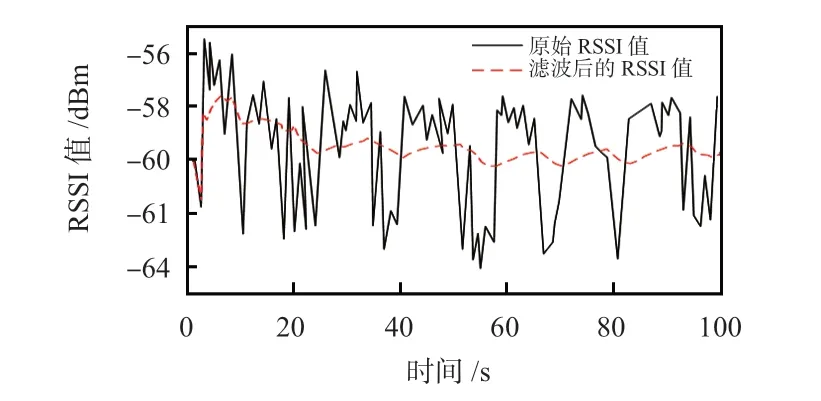
圖3 RSSI數據濾波前、后的效果

2.3 測距網絡優化

在普通地面環境下，收集了大量的地面圖像數據和RSSI測量數據，采用自適應矩估計和BP方法，其中引入了基于平方和平方根的指數加權平均梯度，并利用該值更新參數值［21］。測距網絡優化過程的偽代碼如下

參數含義：a：步長；β1，β2∈［0，1）：矩估計的指數衰減率；f（θ）：參數θ的隨機目標函數；

3 實驗結果與分析

實驗數據采集裝置由RGB攝像頭、儀表尺和無線模塊組成，由一臺計算機完成數據分析，并且裝置運行在2.4 GHz微波頻帶中，RSSI接收器的靈敏度為-97 dBm。動量衰減參數β1為一階矩，一般為0.9，β2為二階矩，一般取0.999，ε一般取10-7。

3.1 數據訓練

所提模型進行測距需要大量訓練數據，包括信號測量數據和圖像數據，使用RGB攝像頭和無線模塊在公共地面環境中收集這些數據，并且使用自適應矩估計梯度降級優化訓練VGG—19網絡。此外，實驗均在帶有Titan X GPU的Ubuntu 16.04 系統上進行，網絡訓練的學習速率為1 ×10-6，一階矩β1和二階矩β2的動量衰減參數分別為0.9和0.999。并且使用均方誤差作為損失函數來訓練和優化模型，直到網絡參數θt收斂。

3.2 誤差估計分析

實驗中，設置了4個場景，分別為理想環境、一般環境、復雜環境和遮擋環境。在所有測試場景中，對所提模型和其他模型計算進行距離估計對比，結果如圖4所示。

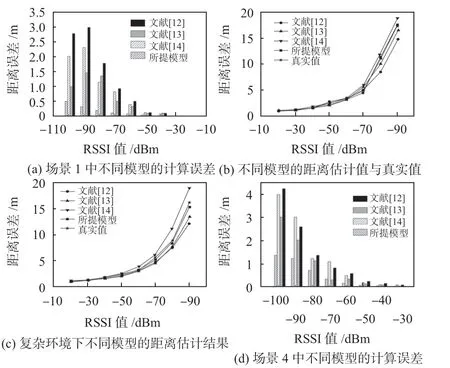
圖4 在4 個場景中不同模型距離估計對比

由圖4（a）可以看出，在理想環境下，隨著RSSI值的增大，距離誤差在不斷增大，但所提模型的距離估計誤差不超過0.5 m，優于其他對比模型。各種模型誤差最大不超過3 m，當RSSI值在-50 dBm以內，距離估計誤差接近0。由圖4（b）可以看出，相比于其他對比方法，一般環境下所提模型的距離估計值與真實值最為接近。尤其是當RSSI 值為-90 dBm 時，文獻［12］的估計值與真實值相差大約為3.5 m，而所提模型的估計值仍與真實值十分接近。由圖4（c）可以看出，場景變得復雜，相比于一般場景，當RSSI值為-90 dBm，所提模型的誤差接近1 m。文獻［14］利用BP神經網絡實現RSSI測距，以及文獻［12］利用DCNN 進行距離估計，兩者均使用單一模型，因此對距離的估計效果不佳，得到的估計值與真實值偏差較大，且抵抗外界干擾的能力較弱。而文獻［13］在BP 網絡的基礎上引入ACO 算法進行優化，估計效果有所提升。由圖4（d）可以看出，遮擋環境下當RSSI值為-20～-50 dBm時，各模型的距離估計誤差均比較小，并且所提模型的估計誤差小于0.1 m。當RSSI值衰減到-60 dBm時，誤差急劇增加，文獻［12］的估計誤差超過4 m。由此可見，遮擋這一因素對測距的精度影響很大，但相對而言，由于所提模型在VGG—19網絡中引入KF，并且進行訓練優化，其得到的距離值誤差較小。文獻［14］提出的BP神經網絡測距模型會產生過擬合現象，因此估計誤差較大。同樣的，文獻［13］在BP神經網絡中引入ACO算法，雖有一定的改善，但效果仍不理想。文獻［12］的DCNN 模型的估計值與實際測量值存在較大的誤差。

3.3 運行效率

由測距時間結果可以看出，所提模型的測距時間為34.92 ms，較文獻［12］的28.18 ms，效率有所降低，與文獻［14］的35.67 ms基本持平。但文獻［12，14］的測距精度不高。而文獻［13］綜合BP神經網絡和ACO算法，測距精度有所提高，但計算效率降低，為46.04 ms。所提模型在VGG—19網絡中引入KF，雖然損失了一定的測距效率，但保證了測距精度，因此整體性能最為理想。

4 結 論

本文提出了基于VGG—19和卡爾曼預處理的WSNs測距方法。在搭建的實驗平臺上，利用數據采集裝置進行實驗分析，結果表明：在4 種不同環境下，所提模型的距離估計誤差均小于其他模型，并且測距時間為34.92 ms，整體性能較為理想。