基于測地線流式核的隱空間多工況軟測量建模*

任 超，葉澤甫，程 蘭，喬鐵柱，閻高偉

（1.太原理工大學 電氣與動力工程學院，山西 太原 030024；2.山西格盟中美清潔能源研發中心有限公司，山西 太原 030000）

0 引 言

由于工業現場高溫高壓、強酸強堿、強干擾等惡劣環境，很難直接采用硬件傳感器監測關鍵質量變量。基于數據驅動的軟測量被研究應用于工業過程中難測參數的在線測量［1～3］。目前，應用領域較為廣泛的數據驅動建模方法有以偏最小二乘（partial least square，PLS）回歸為代表的回歸分析 方 法［4］；高 斯 過 程 回 歸［5，6］、支 持 向 量 機（support vector machine，SVM）［7，8］等基于統計學習發展起來的機器學習方法；以神經網絡為代表的機器學習方法［9，10］等。但是，實際工業生產過程為了滿足產品多樣化的需求，具有多個穩定工況；同時原料和生產環境的改變也會導致工況發生漂移，產生新的運行工況。在新工況缺乏標記樣本時，由于新工況過程數據和歷史工況數據不再服從同樣的概率分布，工況變化造成原有模型失配，對軟測量帶來不利影響。

遷移學習是指從數據標記量充足的源域中學習知識，將其遷移至數據標記量較少甚至沒有標簽的目標域，使得在目標域上取得良好的學習效果。文獻［11］利用源域和目標域數據的全局協方差結構，將2 個域的數據分別投影到對應子空間，學習一種子空間對齊（subspace alignment，SA）的映射函數實現域適應。文獻［12］提出一種聯合分布適配（joint distribution adaptation，JDA）方法，將源域和目標域的邊緣分布和條件分布進行適配，在源域有少量樣本的情況下進行迭代，提高了分類器精度。文獻［13］將測地線流式核引入過程監控，利用主成分分析（principal component analysis，PCA）獲取2 個域各自的差異信息后，在流形空間下進行遷移學習，有效提高了故障診斷的準確率。

由于遷移學習放寬了數據同分布假設，當新工況缺乏標記樣本無法建模時，利用無監督遷移學習，將歷史工況數據與未標記的新工況數據映射到同一空間，使用映射后的歷史工況數據建立模型，不需要從頭開始訓練模型，節約了時間成本。但利用測地線流式核（geodesic flow kernel，GFK）進行域適應時只關注了歷史工況和新工況的過程數據信息，在過程數據分布差異較大但標簽數據分布差異較小的多工況下建模表現良好，卻忽略了歷史工況的標簽信息，導致在標簽變量分布差異較大的多工況下模型會失準。

為提高模型在多工況過程下的適應性，本文首先通過GFK對新工況樣本和已標記的歷史工況樣本的過程變量進行域適應，減小工況過程變量數據分布差異，利用歷史工況的標簽變量和域適應后的數據獲取隱空間投影矩陣，對2個工況間遷移特征進行重構，最后利用支持向量回歸（support vector regression，SVR）模型實現多工況參數軟測量。

1 相關理論與算法

1.1 GFK

GFK［14］方法是指將2個域的子空間分別視為高維格拉斯曼流形空間上的兩點，選擇合適的子空間維度后，構建兩點間測地線，并計算GFK，實現由源域投影變換至目標域的過程。

在多工況運行過程中，假設采集到的歷史工況數據為XS，用二維矩陣形式表示為XS∈Rm×p，采集待測工況數據為XT，用二維矩陣表示為XT∈Rn×p，m 和n 分別為采集樣本數，p為樣本具有的相同特征數。工況遷移過程如下：

1）構建測地線

將歷史工況樣本XS當作源域，待測工況樣本XT當作目標域，利用PCA獲取兩個域的子空間XS，XT。根據兩點間的最短距離定義測地線函數?（t），令?（0）＝PS，?（1）＝PT。兩點間最短距離函數定義為

2）計算GFK

將歷史工況樣本遷移至待測工況，針對兩工況下的樣本點xi和xj，xi，xj∈R1×p，即表示測地線函數從?（0）遷移至?（1），GFK由兩樣本點在測地線函數上的無窮維投影的內積定義［14］

G作為半正定矩陣表述如下

式中 Λ為對角矩陣，Λ1i，Λ2i，Λ3i為對角元素，θi為PS和PT的主角。

1.2 基于PLS的隱空間特征提取

假設某一工況數據ZS有m個樣本，建模變量有p個輔助過程變量｛z1，z2，…，zp｝和q個主導過程變量｛y1，y2，…，yq｝，z，y∈Rm×1，其中，輔助變量矩陣Z ＝［z1，z2，…，zp］，主導變量矩陣Y ＝［y1，y2，…，yq］。利用PLS思想可以提取出既能有效反映工況輔助過程變量信息又能很好地解釋工況主導變量變化規律的潛在特征。根據PLS 原理最終獲取p×r維投影矩陣W ＝［w1，w2，…，wr］，r 為隱變量個數，wr為矩陣EFr-1FEr-1特征值對應的特征向量。E 和F分別為提取主成分過程中對Z和Y的殘差信息進行標準化處理的結果。

2 GFK遷移隱空間投影建模方法

SVM是由Vapnik 等人提出的一種可用于回歸預測以及解決各種分類問題的機器學習方法，數學原理和公式推導詳見文獻［15］。SVR算法具備優異的全局優化性能，在維數較高且具備復雜非線性特點的數據回歸預測應用中展現出了較好的泛化能力［16］。

對于多工況軟測量建模，運用GFK遷移域時將歷史工況作為源域，待測工況作為目標域。將遷移后的歷史工況數據利用PLS獲取投影矩陣W，利用W將域適應后的歷史工況和待測工況數據同時投影至PLS 隱空間，最后利用SVR對PLS隱空間下的重構數據進行建模。本文提出GFK遷移隱空間投影（GFK latent space projection SVR，GFK-LSPSVR）建模方法，圖1為所提建模方法示意。利用SVR建模流程具體如下：

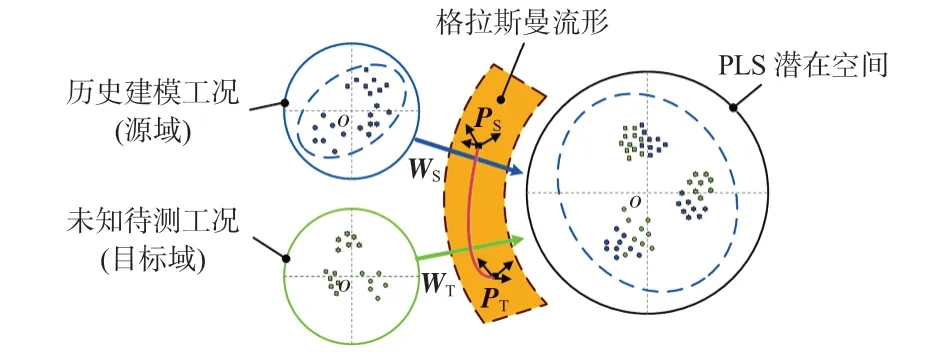
圖1 GFK遷移隱空間投影算法示意

算法1GFK遷移隱空間投影建模流程

輸入：歷史工況a 建模樣本Xa，歷史工況a 數據標簽Ya，待測工況b建模樣本Xb。

輸出：待測工況b數據標簽Yb。

1）利用PCA將Xa、Xb投影到流形空間得Pa、Pb，根據式（1）構建測地線，并根據式（3）求得投影核G，進一步代入式（4）得到域適應后的數據Za、Zb；

2）利用PLS對域適應變換后的Za、Ya計算投影矩陣W；

3）根據W將Za映射到低維隱空間Ta＝ZaW，將Zb映射到同一低維隱空間Tb＝ZbW；

4）基于Ta，Ya建立SVR 預測模型，將Tb代入SVR 模型得到Yb。

3 TE過程仿真研究

3.1 TE仿真設置

本文采用TE 仿真實驗平臺進行多工況軟測量實驗。通過改變反應器壓力和液位來模擬3 種不同工況條件，具體參數設置如表1 所示。選擇15 個過程變量作為被監控變量［17］。對于每一種工況，分別采集1 000個樣本。

表1 TE3 種工況參數設置

將3種工況中的其中一種工況作為歷史數據集，預測另外2種工況下的反應物A，C濃度值。為說明本文GFKLSP-SVR方法的有效性，將其預測結果與SVR，GFK（GFKSVR）遷移回歸以及常用于跨工況遷移軟測量建模的聯合分布適配（joint distribution adaptation SVR，JDA-SVR）遷移回歸，子空間對齊（subspace alignment SVR，SA-SVR）遷移回歸結果進行對比。本文實驗采用均方根誤差（root mean square error，RMSE）指標定量分析不同建模方法下的反應物濃度預測結果，如表2所示。

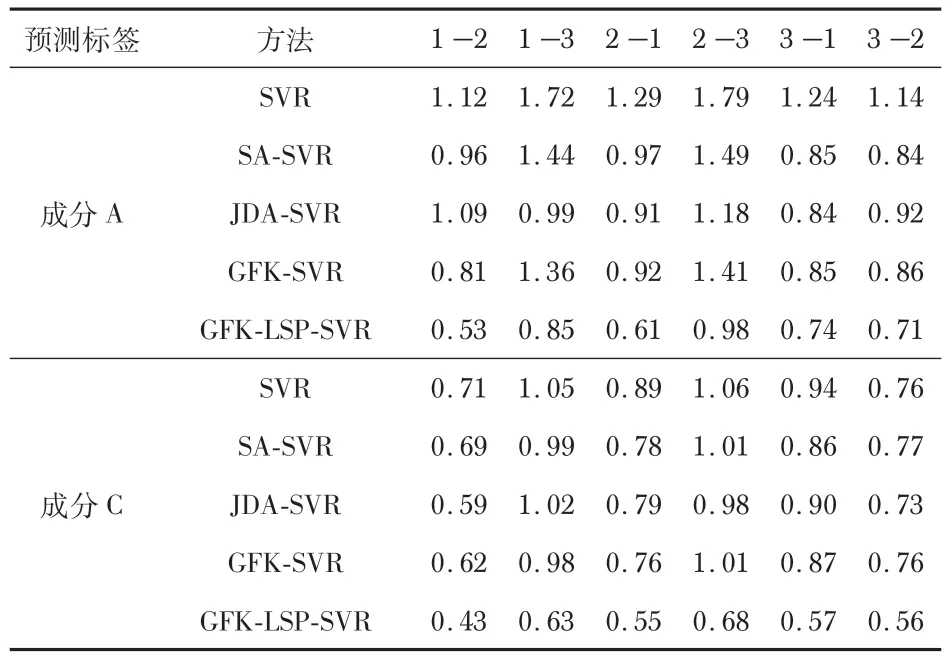
表2 各建模方法軟測量均方根誤差對比結果

圖2分別給出了上述5種建模方法對不同工況下反應物A濃度的預測值，其中橫軸n表示樣本數。

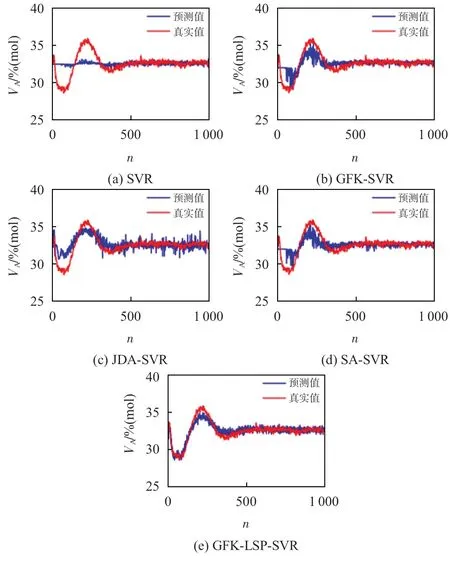
圖2 工況二作為歷史工況對工況一成分A濃度預測

3.2 實驗結果與分析

結合表2和圖2可知，針對非線性工況過程，基于SVR的軟測量模型可以較好地預測穩定趨勢下的工況標簽。但當工況發生改變，尤其工況初期對預測工況前400 個樣本進行標簽估計時，過程變量的均值和方差隨時間變化，其概率分布變化較為明顯，SVR軟測量模型失準；引入遷移學習策略后，JDA-SVR、SA-SVR 方法提取各工況間的方差信息進行域適應，通過適配或對齊工況分布差異信息來提取可遷移特征進行建模。GFK-SVR方法在流形空間下解決域遷移的問題，有效減小了工況過程變量數據分布差異，3 種方法都在一定程度上提高了軟測量精度。本文所提GFKLSP-SVR方法在流形空間域適應基礎上進一步利用工況標簽分布信息重構隱空間特征，提高了建模特征對預測標簽分布信息的表述能力，有效提升了軟測量模型預測精度。主成分分析提取工況一和工況二樣本的主成分，圖3（a）～（c）分別表示兩工況原始樣本、遷移樣本、隱空間遷移樣本的前三維空間表述。由圖中信息可知，兩工況原始數據的空間分布差異較為明顯；引入GFK 框架，在流形空間上充分考慮了工況樣本高維非線性數據的結構特點進行域適應，減小了過程變量分布差異；隱空間投影進一步結合工況數據的差異信息和標簽分布信息重構特征，數據分布更加趨于一致。

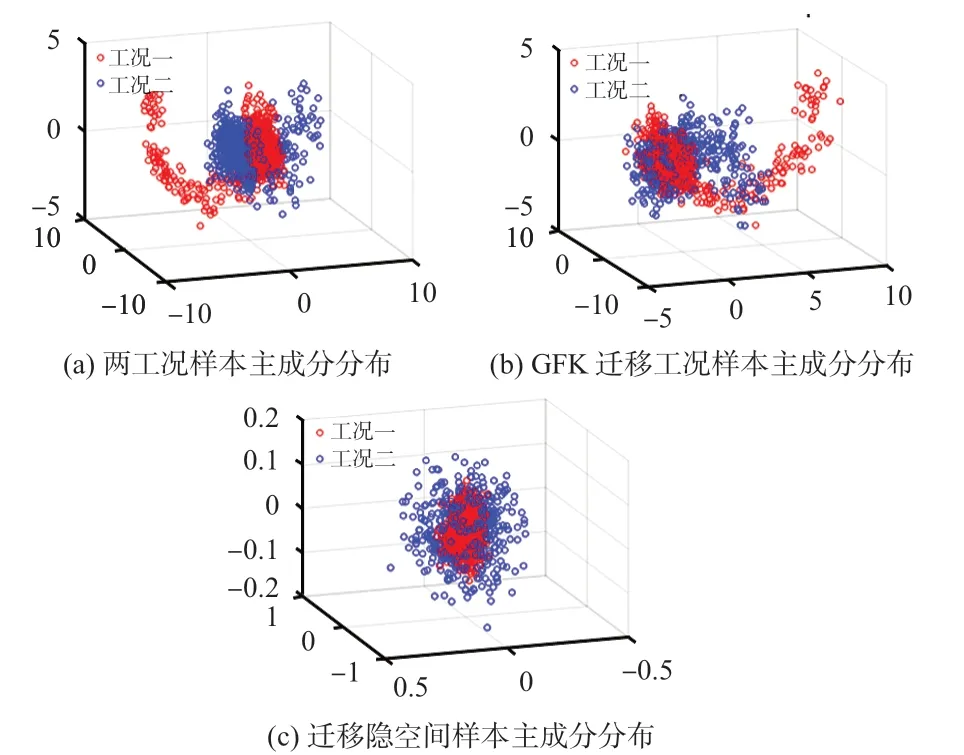
圖3 數據經過域適應以及潛在空間投影的分布示意

4 結 論

針對由于工況數據分布差異而無法有效提升新工況下軟測量模型精度問題，本文在引入GFK減小工況過程變量分布差異的基礎上，利用已有工況的標簽變量信息將域適應特征投影至隱空間后建模。TE 仿真軟測量實驗結果表明，隱空間下的重構特征更加充分利用了多工況數據分布信息，提高了建模精度。