復合多層順傾巖質(zhì)邊坡最優(yōu)錨固角研究

冼 進 業(yè),陳 建 林,李 長 冬,3,冼 樹 興,王 妍

(1.中國地質(zhì)大學 工程學院,湖北 武漢 430074; 2.中國電建集團華東勘測設計研究院有限公司,浙江 杭州 311100; 3.中國地質(zhì)大學 湖北巴東地質(zhì)災害國家野外科學觀測研究站,湖北 武漢 430074)

0 引 言

復合多層順傾巖質(zhì)邊坡是自然界中常見的邊坡類型,在開挖、加載等作用下,往往容易沿軟弱面發(fā)生失穩(wěn)破壞。這類邊坡的整體穩(wěn)定性差,影響交通工程和居民生命財產(chǎn)安全[1-2],開展此類邊坡的加固研究具有非常重要的意義。錨固支護技術作為治理巖質(zhì)邊坡的有效方法之一,具有經(jīng)濟、高效、效果優(yōu)良等優(yōu)點,在滑坡治理、邊坡支護及隧道工程等領域中得到廣泛應用[3-4]。錨固參數(shù)是影響錨桿錨固效果的重要因素之一,因此開展錨固參數(shù)的優(yōu)化研究尤為重要。

王俊石[5]對預應力錨桿的作用機理進行研究,確定了錨固角是優(yōu)化的關鍵因子,并提出了最優(yōu)化錨固角的確定與應用方法。熊文林等[6]研究了坡面與滑面傾角對最優(yōu)錨固角計算的影響,認為原有的規(guī)范推薦計算方法是坡面與滑面傾角相同時的特例,并提出了確定最優(yōu)錨固角的新方法。張發(fā)明等[7]基于優(yōu)化與決策理論,分析了影響錨固支護設計的因素,建立起錨固支護設計的決策支持系統(tǒng)。封金財[8]從錨桿自由段與錨固段的長度關系入手分析,推導出單位長度錨桿提供最大抗滑力時的錨固角計算公式。王朝陽等[9]考慮土體中間主應力影響,基于統(tǒng)一強度理論利用最優(yōu)錨固長度與錨固角的關系曲線,提出了確定錨桿最優(yōu)錨固長度與錨固角的方法。劉駿等[10]運用UDEC模擬了不同錨固參數(shù)下錨桿對邊坡加固效果的影響,結果表明錨固角對錨桿的錨固效果影響最大。

上述研究為錨固工程設計提供了重要的研究基礎,但當前錨固系統(tǒng)設計往往將加固段巖層視為均質(zhì)巖層[11],然而,巖體在成巖過程中,由于沉積環(huán)境的變化導致物質(zhì)組成、粒徑、礦物結構等差異,巖層往往具有分層性和互層性[12-13],這種地層結構在自然或人工邊坡中普遍存在,因此均質(zhì)地層錨固支護模型有一定的條件限制。

鑒于此,本文采用統(tǒng)一強度理論,推導出復合多層巖體錨桿極限抗拔力公式,并提出復合多層順傾巖質(zhì)邊坡的最優(yōu)錨固角模型與最優(yōu)錨桿長度的確定方法。同時,將本文方法運用到三峽庫區(qū)巴東縣一公路邊坡工程中,將其與規(guī)范法及傳統(tǒng)庫倫理論計算的錨桿長度進行對比研究。

1 理論背景

俞茂宏[14]提出的統(tǒng)一強度理論能夠靈活地適應各類材料的特點,并能考慮中間主應力效應,而目前常用的理論往往忽略中間主應力對材料破壞的影響[15]。因此,對于應力狀態(tài)復雜的邊坡巖體而言,統(tǒng)一強度理論更能真實地反映巖體的應力狀態(tài),巖土體的應力表達式如下[16]:

(1)

(2)

式中:c0為巖土體材料黏聚力,kPa;φ0為內(nèi)摩擦角,(°);b為中間主剪應力對材料破壞的影響系數(shù),對于確定的巖土體而言,0≤b≤1,為了方便計算,本文設b=1。

俞茂宏等[17]和Lee等[18]增加了中間主應力影響系數(shù)m,對統(tǒng)一強度理論進一步推導,求得了中間主應力與最大、最小主應力的關系式為σ2=m(σ1+σ3)/2,0≤m≤1。文獻[19]研究表明,對于平面應變問題,在塑性區(qū)內(nèi)m趨近于1。唐仁華等假定m=1,結合莫爾-庫倫理論推導出了統(tǒng)一強度理論下抗剪強度參數(shù)與莫爾-庫倫理論抗剪強度參數(shù)的變換公式[20]:

(3)

式中:ct和φt分別為統(tǒng)一強度理論下巖土材料的黏聚力和內(nèi)摩擦角。

2 概化模型

如前所述,在自然界中含軟弱夾層的復合多層順傾巖質(zhì)邊坡普遍存在,其巖體強度不具備連續(xù)性,容易沿軟弱面發(fā)生破壞[21-22],因此亟需開展此類邊坡的錨固支護研究。本文根據(jù)該類邊坡的特點,參考文獻資料[1,23-25],概化出復合多層順傾巖質(zhì)邊坡錨桿加固模型,如圖1所示。

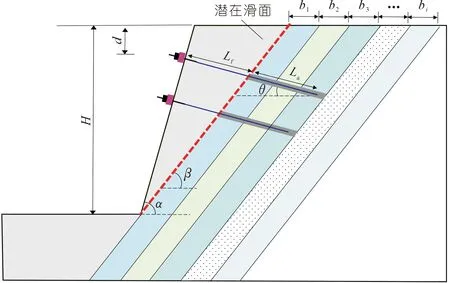
注:bi為第i層圍巖出露長度

圖1中:α、β、θ分別為邊坡坡角、巖層傾角和錨固角;H為坡高;d為加固點到坡頂?shù)拇怪本嚯x;Lf和La分別為錨桿自由段和錨固段長度。

2.1 復合多層巖體錨桿極限抗拔力計算

錨桿的作用機理復雜,導致錨固系統(tǒng)的失效模式多樣。國內(nèi)外學者通過原位試驗與力學理論研究了錨桿的破壞形式及其破裂面形態(tài)[26-29]。鄧宗偉等[29]根據(jù)前人試驗統(tǒng)計認為錨桿以復合型破壞為主,即錨桿淺部伴隨錐形或圓弧形破壞,在破裂面以下的桿體發(fā)生滑移破壞,此類破壞形式為拉拔型破壞,錨桿的承載能力取決于其極限抗拔力,此外其研究還表明錐形破壞部分提供的抗拔力很小。因此,錨桿極限抗拔力是由注漿體與圍巖間接觸面強度參數(shù)及圍巖壓力決定的。

本文以全長粘結型錨桿為對象,根據(jù)錨桿錨固段與圍巖的作用方式及破壞特點,假設錨固段在各巖層剪應力均勻分布,當錨固體發(fā)生滑移破壞時,其受力條件如圖2所示。在文獻[20]的基礎上,考慮注漿體與各巖層的接觸面強度參數(shù)差異,在復合多層巖體條件下錨桿極限抗拔力表述為

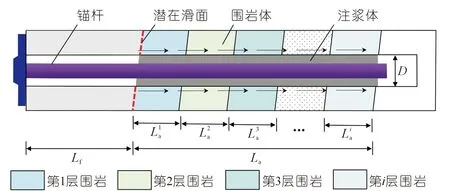
圖2 復合多層巖體錨桿作用方式

(4)

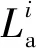
(5)

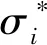
(6)

2.2 復合多層順傾巖質(zhì)邊坡錨桿錨固段長度計算

根據(jù)圖1的地質(zhì)模型對其進行極限平衡分析。滑體受到沿層面向下的推力,同時受到由巖層間的摩擦和黏聚作用形成的抗滑力,在錨桿的支護作用下,邊坡的穩(wěn)定性系數(shù)計算公式如下[30]:

Tsin(θ+β)tanφ]

(7)

式中:L為滑面長度,L=H/sinβ;c、φ為滑面的黏聚力與內(nèi)摩擦角;G為滑體重量,G=γ0H2sin(α-β)/(2sinβsinα)。對公式(7)進一步推導,在邊坡穩(wěn)定性系數(shù)確定情況下錨桿群所需提供的錨固力計算公式為

(8)

當錨固力T由全部錨桿提供時,設錨桿布置n排,其水平間距為a,在考慮一定安全儲備情況下,則單根錨桿所需的錨固力為

(9)

式中:K為錨桿安全系數(shù)。

在無外部觸發(fā)因素的影響下,復合多層順傾巖質(zhì)邊坡的單根錨桿錨固段長度可用式(10)計算:

(10)

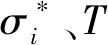
3 復合多層巖質(zhì)邊坡最優(yōu)錨固角模型

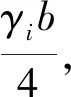
(11)

式(11)中自由段Lf是關于錨固角θ變化的函數(shù),因此需要確定其表達式。在加固點位置確定時,當錨桿與巖層面垂直時自由段長度達到最小值,設此時的自由段長度為Lmin,對于其他情況下的自由段長度可表示如下:

(12)

由式(8)、(9)得單根錨桿所需要的錨固力,聯(lián)立式(11)、(12)得單根錨桿的錨固段長度公式:

(13)

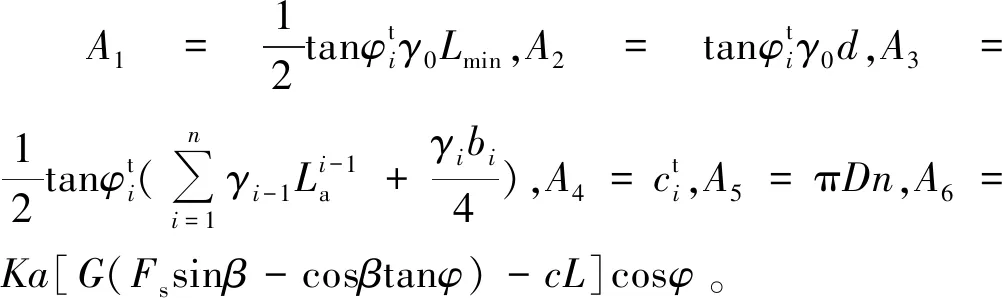
由式(13)得到單根錨桿的錨固段長度公式,但錨桿總長是由自由段長度與錨固段長度共同決定的,聯(lián)立式(12)、(13)得到錨桿總長L總的表達式:

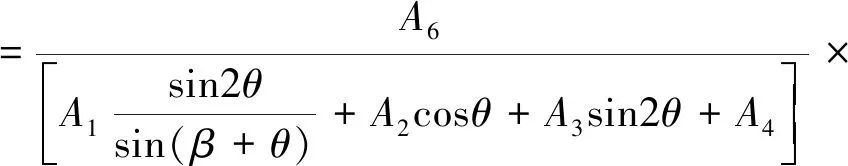
(14)

錨桿單位長度提供的抗滑力增量為

(15)

式中:Pt=Ni[sin(β+θ)tanφ+cos(β+θ)],J(θ)是關于錨固角θ變化的函數(shù),存在θ0使其達到最大值,當達到最大值時,單位長度錨桿提供的抗滑力增量最大,可認為θ0為最優(yōu)錨固角[8]。

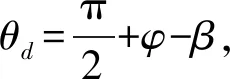
(16)

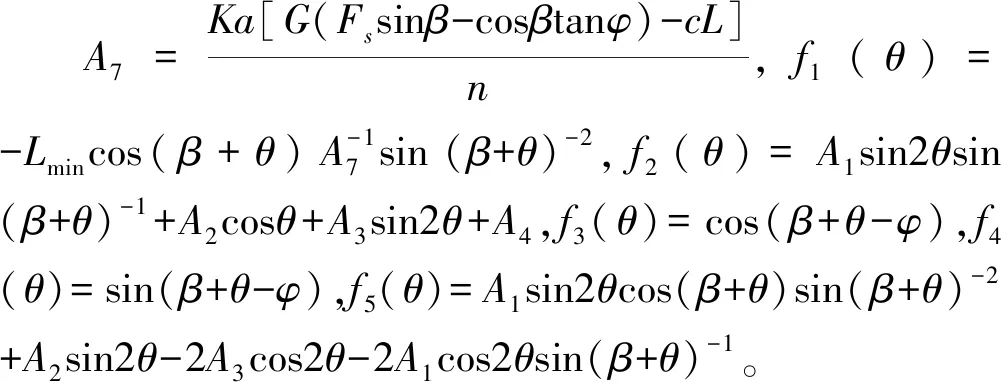
要求取F(θ)在錨固角施工區(qū)間內(nèi)的最小值,即要判斷F(θ)在區(qū)間端點和求導函數(shù)異號零點處的大小關系。由于最優(yōu)錨固角模型F′(θ)形式復雜,直接求取異號零點精確值的難度大,而在傳統(tǒng)的錨固支護工程中一般以整數(shù)角度施工,故可通過二分法對上述F′(θ)函數(shù)的異號零點所在區(qū)間端點進行逼近,進而得到函數(shù)異號零點的近似值。式(16)中A1、A2、A3、A4與錨固微元體所在的巖層有關,故需要對不同巖層中的最優(yōu)錨固角進行遞歸運算,以確定最優(yōu)錨固角所在的區(qū)間范圍。

4 工程案例分析

4.1 邊坡案例介紹

擬研究的公路邊坡位于三峽庫區(qū)湖北省巴東縣,邊坡概化圖如圖3所示。其地層巖性為三疊系中統(tǒng)巴東組中風化灰?guī)r與強風化泥質(zhì)灰?guī)r互層[30],巖層順傾坡,巖層傾角22°,體高約28 m,邊坡坡角為38°。根據(jù)文獻[30-31],各巖體的參數(shù)如表1所列。經(jīng)極限平衡法分析,灰?guī)r與泥質(zhì)灰?guī)r的接觸面被確定為最危險潛在滑面,滑面傾角22°,在未進行支護下邊坡穩(wěn)定性系數(shù)為1.091。規(guī)范規(guī)定當邊坡穩(wěn)定性系數(shù)Fs小于1.3時[32],需要對其進行支護。由于公路邊坡危害大、威脅公共安全,因此以一級邊坡對其進行錨固設計[33]。對邊坡進行支護,擬定支護后邊坡穩(wěn)定性系數(shù)Fs為1.4,錨桿安全系數(shù)K為2.2,錨桿布置6排,水平間距為2.8 m,鉆孔直徑D為110 mm,首個加固點位置距坡頂垂直距離6 m,錨桿支護設計方案見圖3。

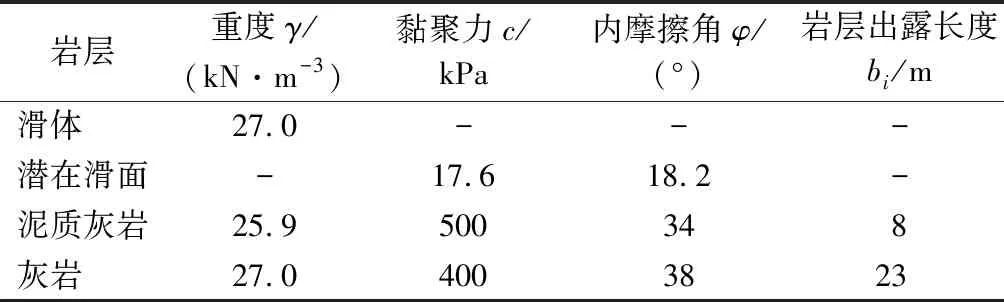
表1 公路邊坡物理力學參數(shù)

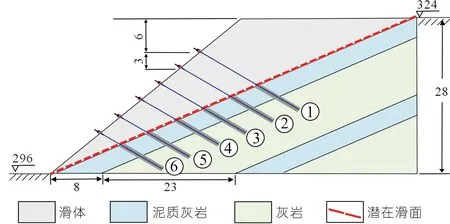
圖3 邊坡錨固工程模型概化(尺寸單位:m)

4.2 最優(yōu)錨固角與最優(yōu)錨桿長度

以圖3編號①錨桿為例,介紹利用最優(yōu)錨固角模型求取最優(yōu)錨固角的詳細過程。考慮該案例各巖層厚度與錨桿所需的錨固力,假設微元體分別處于第一層泥質(zhì)灰?guī)r和第二層灰?guī)r(i=1,2),據(jù)文獻[34]擬定錨桿注漿體與灰?guī)r、泥質(zhì)灰?guī)r界面的黏聚力分別為329,308 kPa,摩擦角34.21°,32.91°,代入式(15)中,經(jīng)二分法計算零點θ0分別為34.5°和37.2°。函數(shù)F′(θ)零點分布如圖4所示。

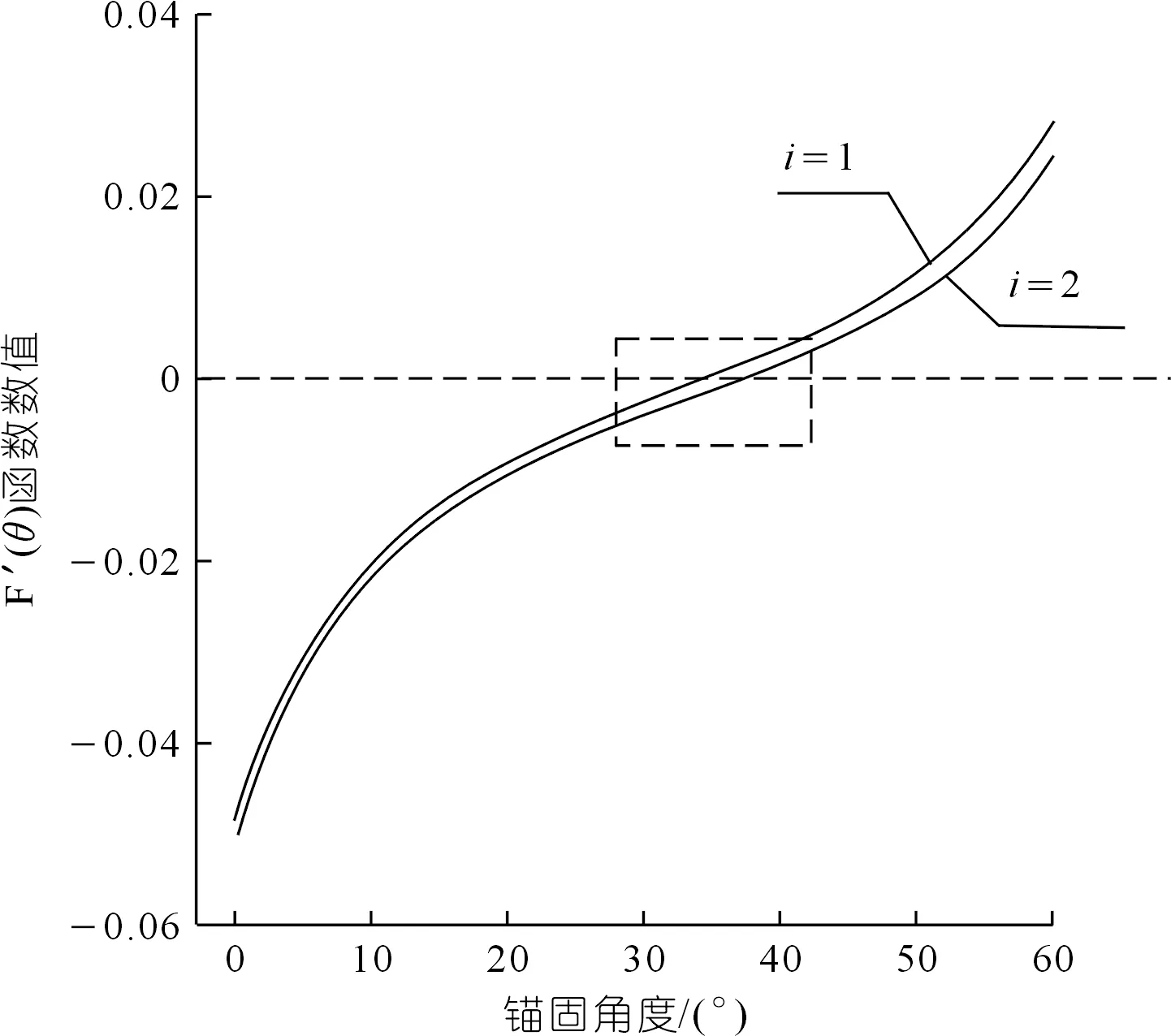
圖4 最優(yōu)錨固角模型F′(θ)函數(shù)零點分布

對二分法計算結果分析認為最優(yōu)錨固角在34°～37°內(nèi),為了進一步確定最優(yōu)錨固角,分別以該范圍內(nèi)錨固角布置錨桿,各錨固角邊坡單位寬度全部錨桿總長度分布見表2。

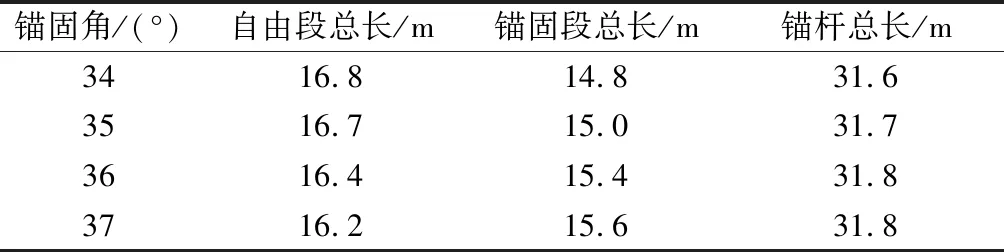
表2 各錨固角邊坡單位寬度全部錨桿總長度分布

由表2可知,在錨固角度34°～37°范圍內(nèi),單位寬度全部錨桿總長度范圍在31.6～31.8 m之間,各角度間單寬錨桿總長差距較小,總長最大值與最小值僅差0.6%,其中,當錨固角度為34°時,單寬錨桿總長度最小,且符合規(guī)范推薦的錨固角范圍(10°～35°)[32],因此,本文以34°作為最優(yōu)錨固角,并以該角度布置錨桿,各編號錨桿長度分布如圖5所示。

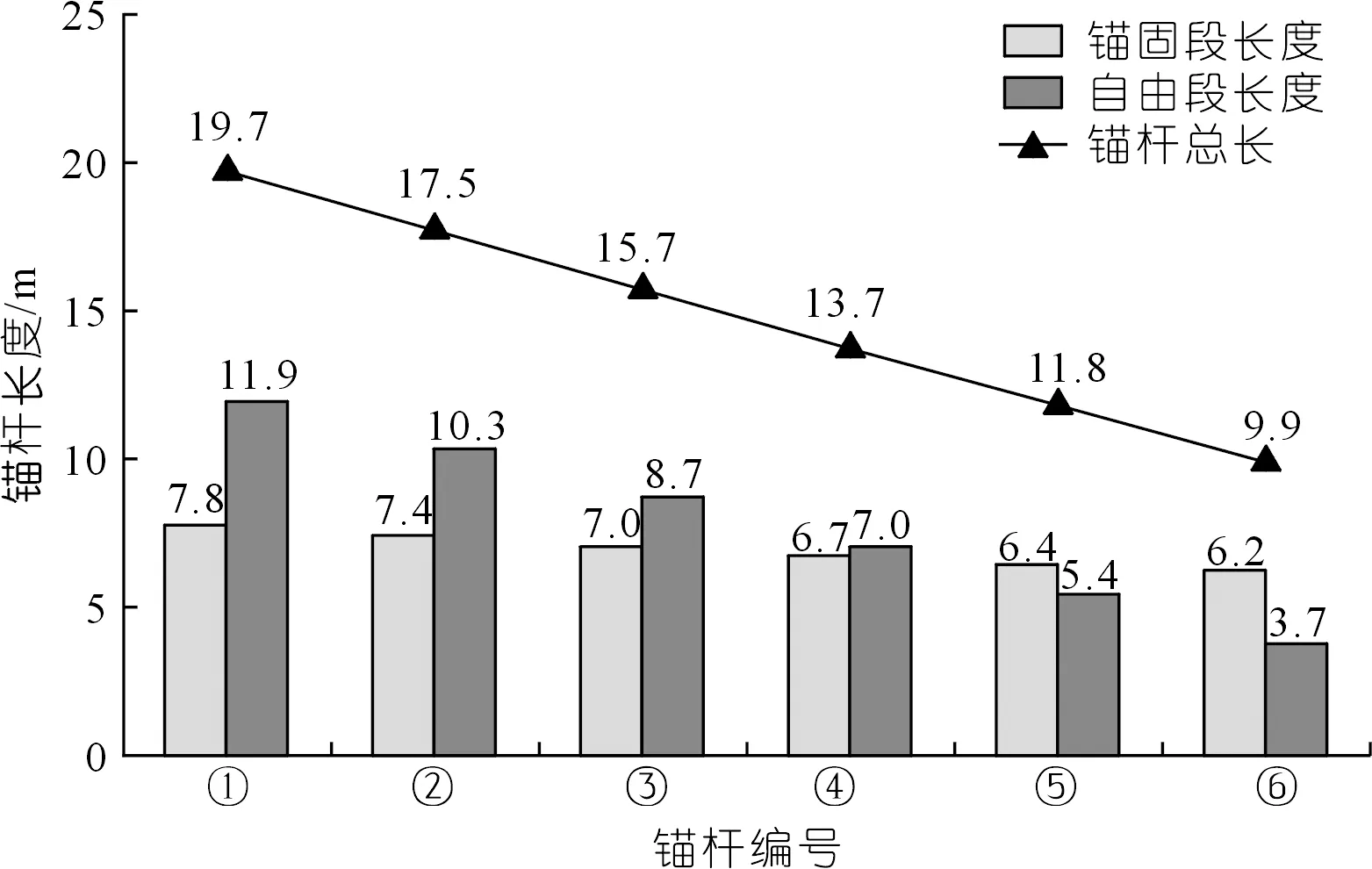
圖5 錨固角34°下各錨桿長度分布

4.3 最優(yōu)錨固角度模型驗證

為了驗證最優(yōu)錨固角度模型的正確性,通過均勻試驗方案對本文所提方法進行驗證。在保證條件相同的情況下,現(xiàn)取錨固角θ分別為10°,15°,20°,25°,30°,35°,40°等7種工況對案例邊坡錨桿長度進行計算,邊坡單位寬度全部錨桿總長計算結果如圖6(a)所示。

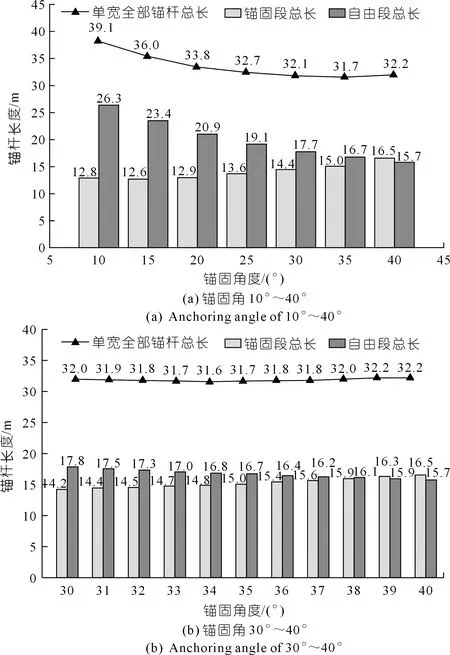
圖6 錨固角度與單位寬度全部錨桿總長度關系

由圖6(a)可知,對錨固段而言,當錨固角在10°～20°范圍內(nèi),錨固段總長變化幅度較小,在15°～40°范圍內(nèi),錨固段總長呈上升趨勢。對單寬全部錨桿總長而言,當錨固角在10°～35°范圍內(nèi),錨桿總長隨錨固角的增大而減少,在35°～40°范圍則呈相反趨勢。在30°～40°范圍內(nèi)錨桿總長差距較小,35°時錨桿總長達到局部最小值,由此可見最優(yōu)錨固角在30°～40°范圍內(nèi)。

圖6(b)顯示了錨固角30°～40°范圍內(nèi)錨桿長度的變化情況,在該范圍內(nèi)單寬錨桿總長變化趨勢平緩,當錨固角為34°時,錨桿總長達到最小值,可確定34°為最優(yōu)錨固角,與本文最優(yōu)錨固角模型方法求取結果一致。

4.4 與規(guī)范及傳統(tǒng)理論方法對比

為了驗證本文方法的適用性,利用規(guī)范法及傳統(tǒng)摩爾-庫侖理論對該公路邊坡進行錨固支護設計,錨桿加固點位置、錨桿排數(shù)、錨桿安全系數(shù)及支護后邊坡穩(wěn)定系數(shù)與上文設定一致,對比單位寬度所需的錨桿總長。

4.4.1與規(guī)范推薦方法計算的錨桿長度對比

根據(jù)規(guī)范,在確定錨桿所需錨固力后,錨固段長度可用式(17)表示[33]:

(17)

式中:La為注漿體與巖層的錨固長度,m;Ni為單根錨桿提供的錨固力,kN;fmg為注漿體與巖層間的黏結強度,kPa;D為鉆孔直徑,mm;ψ為錨固段長度與對巖層極限黏結強度的影響系數(shù)。

采用規(guī)范推薦錨固角對公路邊坡進行支護,規(guī)范推薦錨固角如式(18)所示[33]:

(18)

將該公路邊坡的參數(shù)及潛在滑面參數(shù)代入式(18),計算得到最優(yōu)錨固角為32°。該邊坡以強風化泥質(zhì)灰?guī)r及中風化灰?guī)r為主,根據(jù)巖層性質(zhì)按文獻[35],擬定注漿體與強風化泥質(zhì)灰?guī)r粘結強度fmg為400 kPa,與中風化灰?guī)r黏結強度fmg為1 000 kPa,ψ按規(guī)范建議值取0.8,計算得該公路邊坡單位寬度所需的錨桿總長為35.6 m。比較可知,文本理論方法計算邊坡單寬所需錨桿總長(31.6 m)比規(guī)范法計算所得錨桿總長減少11.2%。

4.4.2與傳統(tǒng)莫爾-庫倫理論計算的錨桿長度對比

基于傳統(tǒng)莫爾-庫倫理論,確定錨桿所需的錨固力后,在不考慮中間主應力下,錨桿穿越復合多層巖層時錨固段長度可按式(19)計算:

(19)

在不考慮中間主應力下,將注漿體與巖體接觸面的傳統(tǒng)強度參數(shù)黏聚力與摩擦角(見4.2節(jié))代入式(16)中,求得最優(yōu)錨固角為33°,計算得該公路邊坡單位寬度所需的錨桿總長為34.7 m。對比發(fā)現(xiàn),基于統(tǒng)一強度理論的計算結果(31.6 m)相比于傳統(tǒng)庫倫-理論計算所得的錨桿總長減少8.9%。

5 討 論

文獻[9]采用統(tǒng)一強度理論,通過最優(yōu)錨固長度與錨固角的關系,提出了考慮中間主應力的錨桿最優(yōu)錨固長度與錨固角的確定方法。為了體現(xiàn)本文最優(yōu)錨固角模型計算方法與該方法的差異,利用文獻[9]方法對案例邊坡進行支護設計,各參數(shù)與4.1節(jié)設定一致,求得單位寬度全部錨桿最優(yōu)錨固長度與錨固角的關系如圖7所示。單寬全部錨桿最優(yōu)錨固總長取曲線最小值12.6 m,對應最優(yōu)錨固角為15°,單位寬度全部錨桿總長為36 m,多于本文計算方法13.9%。該方法通過錨桿最優(yōu)錨固段長度確定錨固角,但錨桿總長是由錨固段和自由段共同決定的。本文計算方法則是通過錨桿單位長度提供的抗滑力增量確定最優(yōu)錨固角,綜合考慮了自由段和錨固段的變化情況,使最優(yōu)錨固角的確定更具全局性。

6 結 論

(1) 基于統(tǒng)一強度理論,由錨桿的失效模式及其作用方式,推導出在復合多層巖體中錨桿的極限抗拔力計算公式。根據(jù)錨固段微元體與所在巖層的單位長度抗力比,提出了復合多層順傾巖質(zhì)邊坡最優(yōu)錨固角模型。最優(yōu)錨固角與微元體所處巖層有關,可依據(jù)錨固段穿越巖層數(shù)量對最優(yōu)錨固角度范圍進行精確限定,對比其錨桿長度確定最優(yōu)錨固角度。

(2) 將本文所提方法應用于三峽庫區(qū)巴東縣一公路中風化灰?guī)r與強風化泥質(zhì)灰?guī)r互層巖質(zhì)邊坡工程。計算表明在最優(yōu)錨固角模型限定范圍內(nèi),34°單位寬度錨桿總長最小(31.6 m),各錨固角間單寬全部錨桿總長差距較小(31.6～31.8 m),最大值與最小值相差僅為0.6%。通過均勻?qū)嶒灧桨笇Ρ疚乃岱椒ㄇ蟮玫淖顑?yōu)錨固角度進行了驗證,結果表明與本文方法計算結果一致。

(3) 在相同的邊坡穩(wěn)定性系數(shù)下,利用本文方法對案例邊坡進行支護設計,計算所得單位寬度全部錨桿所需總長(31.6 m)相比于規(guī)范推薦方法計算結果(35.6 m)減少11.2%,相比于傳統(tǒng)莫爾-庫倫理論計算結果(34.7 m)減少8.9%,優(yōu)化顯著。

研究結果可為類似的復合多層順傾巖質(zhì)邊坡的錨固支護設計提供一定的借鑒與參考。