杭州灣海域橋梁承臺水平方向波浪荷載研究

董 偉 良,邵 杰,2,黃 世 昌,閆 杰 超

(1.浙江省水利河口研究院(浙江省海洋規劃設計研究院),浙江 杭州 310020; 2.河海大學 港口海岸與近海工程學院,江蘇 南京 210098; 3.中鐵大橋勘測設計院集團有限公司,湖北 武漢 430101)

0 引 言

中國跨海橋梁的橋墩一般采用大型沉井或高樁承臺結構,沉井結構相對簡單,計算方法較多,而由樁基、承臺和墩身組成的高樁承臺結構,水平方向波浪荷載計算十分復雜。樁基和墩身平面結構尺寸相對較小,水平方向波浪荷載直接采用Morison公式就可較準確地計算出來,中、美、英規范均采用該方法[1]。因承臺平面尺寸相對較大,小尺度結構物受力計算方法已不適用,且承臺會產生波浪散射,干擾入射波浪場,繼而影響承臺受力,使得承臺受力分析變得復雜許多。

目前常采用波浪繞射理論計算大尺寸結構物波浪荷載,美國《海上移動鉆井平臺建造和入級規范》、英國《海工建筑物》、德國《勞式規范和準則》、日本《港灣設計技術標準及編制說明》和中國《港口與航道水文規范》等均如此,但現有規范尚無明確的承臺水平方向波浪荷載計算公式,一般采用橋墩波流力數值計算或通過物理模型試驗進行研究[2-6]。為此,許多學者也進行了相關研究,李劍等[7]分析了Morison方程、繞射理論和CFD不同方法計算承臺波浪荷載的差異。張胡等[8]以線性波浪繞射理論為基礎,建立了大尺度結構波浪荷載三維數學模型,研究了大尺度結構波浪荷載。鄧莎莎等[9]基于繞射理論研究了大尺度橋墩波浪荷載計算方法。孫冰等[10]通過物理實驗與數值模擬的對比,分析了樁基承臺結構在計算波浪荷載時的計算方法。徐博等[11]通過建立波浪與高樁承臺相互作用三維數值模型,研究了承臺波浪荷載時程特性、承臺周圍流場以及凈空對水平方向波浪荷載的影響規律。

由于承臺在波浪作用下的受力分析缺乏相關規范和簡易快速計算方法,在實際應用過程中缺乏科學指導,因此對跨海橋梁承臺水平方向波浪荷載進行研究十分必要。基于此,本文以杭州灣海域波浪條件和跨海橋梁承臺結構尺寸為參考,采用矩形概化承臺進行承臺波浪荷載數值模擬,并在此基礎上給出了承臺水平方向波浪荷載計算方法,繼而探討了承臺形狀和流速對波浪荷載的影響。

1 杭州灣波浪條件

杭州灣地理形狀為喇叭形,灣內水深從南向北總體上由淺變深,其中分布有不少島嶼,北部有深槽,灣內波浪受地形和灣口舟山群島影響而變得復雜。杭州灣附近波浪測站主要有嵊山站、大戢山站、灘滸站、乍浦站、外游山站等,具體位置見圖1。根據茹榮忠等[12]實測結果可知,大戢山站實測最大波高為7 m左右,灘滸站實測最大波高為4 m左右,大游山實測最大波高為5 m左右,乍浦站實測最大波高為6 m左右。

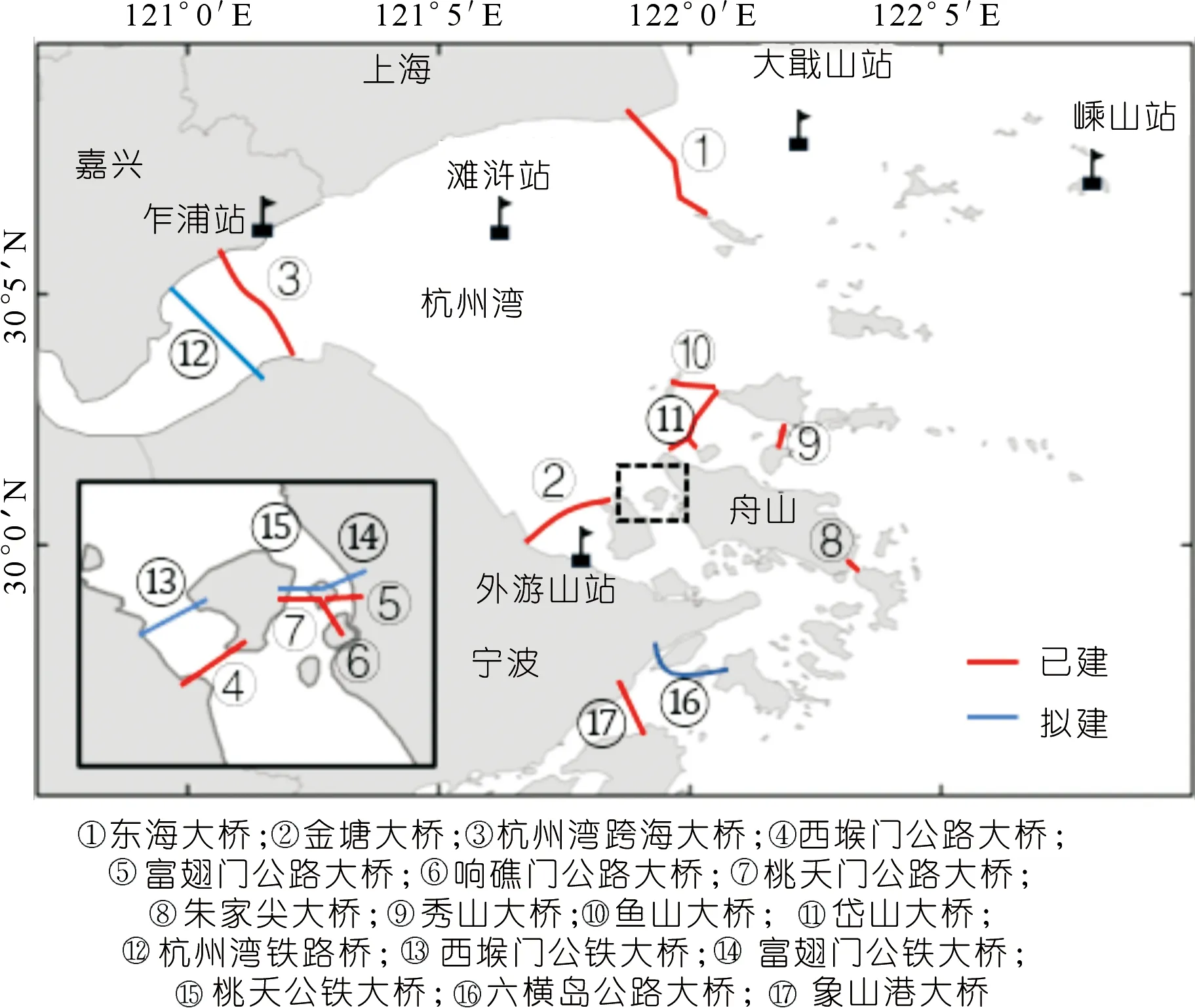
圖1 杭州灣海域波浪站和跨海橋梁分布

杭州灣波浪整體以風浪為主,其中部、東北部和東部的波浪較北部及西北部的大,舟山群島東部海域受風浪和涌浪同時作用,波浪周期比杭州灣內大,其中嵊山站、大戢山站、灘滸站、乍浦站年、外游山站年最大波周期分別為19,8,6,8 s左右。自然資源部第二海洋研究所分別于2009～2010年對杭州灣中部、2014～2015年對舟山島東北部海域臺風浪進行實地測量,研究發現杭州灣內譜峰周期范圍為2～13 s,舟山群島東北海域譜峰周期基本在4～14 s[13-14]。

2 杭州灣橋梁概況

環杭州灣地區位于中國經濟發達的長三角,周邊有上海、杭州、寧波等大都市,以及寧波舟山港、上海洋山深水港這兩個億噸大港,對跨海橋梁有著巨大需求。如圖1所示,近年來杭州灣、舟山群島海域已建設了諸多跨海橋梁,如東海大橋、金塘大橋、杭州灣跨海大橋、秀山大橋、魚山大橋、岱山大橋,近期還將建設多座跨海大橋,如杭州灣鐵路橋、西堠門公鐵兩用大橋、六橫大橋等,未來還將規劃實施滬甬及滬舟甬跨海大通道等,使得該區域形成具有一定規模的跨海橋梁群。

圖2為杭州灣海域部分跨海橋梁通航孔主墩、輔助墩、過渡墩等主要橋墩的承臺尺寸(部分含防撞設施)。從圖中可知,通航孔承臺橫橋向長度基本在20～80 m,順橋向長度基本在15～55 m。

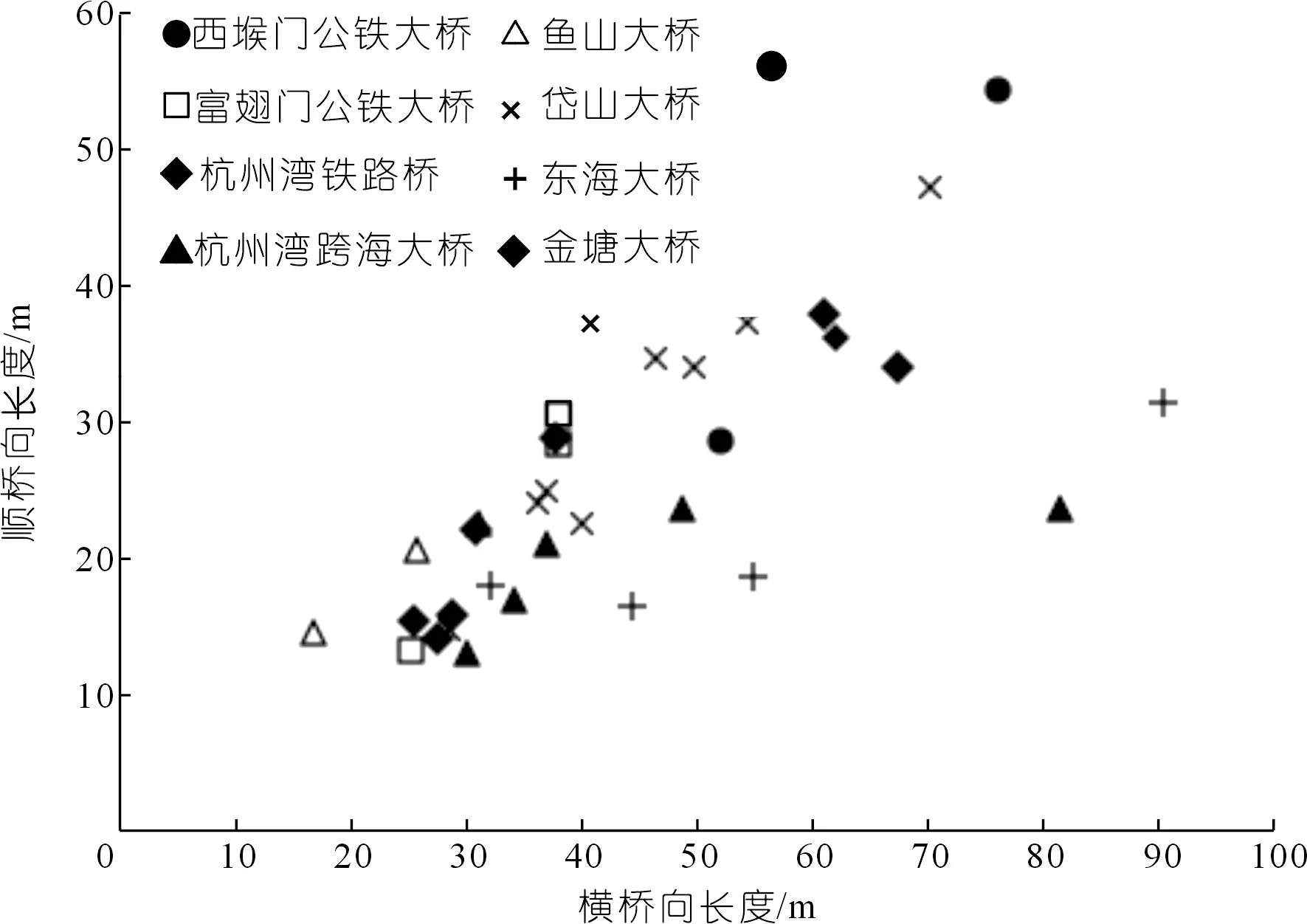
圖2 杭州灣海域主要跨海橋梁承臺尺寸

3 研究方法

3.1 承臺水平方向波浪荷載數值計算

通過FLUENT軟件平臺建立橋梁承臺水平方向波浪荷載數值水槽模型,模型計算結果和跨海大橋橋墩波流力物理模型試驗結果吻合良好[15]。

由于杭州灣海域橋梁承臺形式多種多樣,為方便研究,采用矩形承臺結構來統一概化承臺形狀,在計算過程中承臺長度l1(沿波浪傳播方向)選取20,40 m和80 m,承臺寬度l2=40 m(垂直波浪傳播方向)保持不變,承臺頂、底高程統一取6 m和-2 m,海底高程取為-20 m。

根據杭州灣海域波浪條件,考慮到平常和極端波況,波高H選擇2,3,4 m和5 m共4種,波浪周期T選擇8,10,12 s和14 s共4種來進行橋梁承臺水平方向波浪荷載研究。

3.2 承臺水平方向波浪荷載計算公式

假定波浪是不可壓縮的理想流體,流場中存在速度勢。如果入射波為波高足夠小的線性波,并且墩柱結構物上的波浪力可采用線性理論,此時波浪繞射問題為線性繞射問題。

由于圓柱的線性波繞射問題有解析解,在公式推導過程中一般考慮圓形截面,根據MacCamy-Fuchs繞射理論進行推導,則作用在某深度圓柱截面上的單位長度水平荷載F為

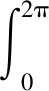
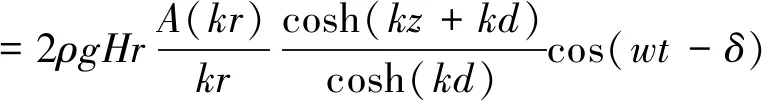
(1)

式中:ρ為水體密度;g為重力加速度;H為波長;r為圓柱半徑;k為波數;z為圓柱截面相對水面所在位置;d為水深;t為時間;w為圓頻率;δ為初始相位。

式(1)中第一個r表示圓形承臺阻水長度,則矩形承臺中第一個r可用矩形承臺寬度l2的一半進行替換;A(kr)/kr表示圓形承臺半徑和波長的關系,則矩形承臺中此處r可用矩形承臺長度l1的一半進行替換。然后在承臺高度范圍內,沿垂向積分求得承臺水平方向波浪荷載最大值為

(2)

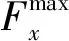
4 計算結果分析

4.1 承臺水平方向波浪荷載系數確定

將不同淹沒度、波高、周期、承臺長度等條件下的承臺水平荷載計算值[15]按式(2)反算得出的A(kb)/kb繪制于圖3中。從圖中可以看出A(kb)/kb隨kb增大而先增后減,當kb為1～1.5時存在最大值。根據數值計算結果,擬合出A(kb)/kb的變化關系式為

(3)

式中:α為系數,此處取α=3.0;β為A(kb)/kb取最大值時kb的值,此處取1.2。從圖3中可以看出,當kb為0.3～3時,式(3)計算值和數值計算結果吻合較好,可基本反映A(kb)/kb隨承臺相對長度kb的變化關系。

圖4為Nojiri[16]、Tanizawa[17]和 Koo[18]等的研究成果和式(2)計算結果的對比,從圖中可以看出式(2)計算結果和前人研究成果基本一致。為方便起見,將式(2)改寫成和Morison方程中水平荷載慣性項同樣的形式,得到慣性力系數CM為

(4)

4.2 形狀對承臺水平方向波浪荷載影響

選用直徑為40 m的圓形承臺和長寬均為40 m的矩形承臺作為研究對象。圖5是通過數值水槽計算圓、矩形承臺水平方向波浪荷載反算得到的A(kb)/kb隨kb變化規律,其中,波高H=2 m,波周期T為8,10,12 s和14 s。從圖中可以看出矩形承臺A(kb)/kb值大于圓形承臺。由于矩形承臺存在棱角,在波動場中波浪更容易產生渦及渦脫落現象,圓形承臺幾乎不產生渦及渦脫落現象,矩形承臺對波浪的阻擋作用更為明顯,繼而矩形承臺水平荷載更大。

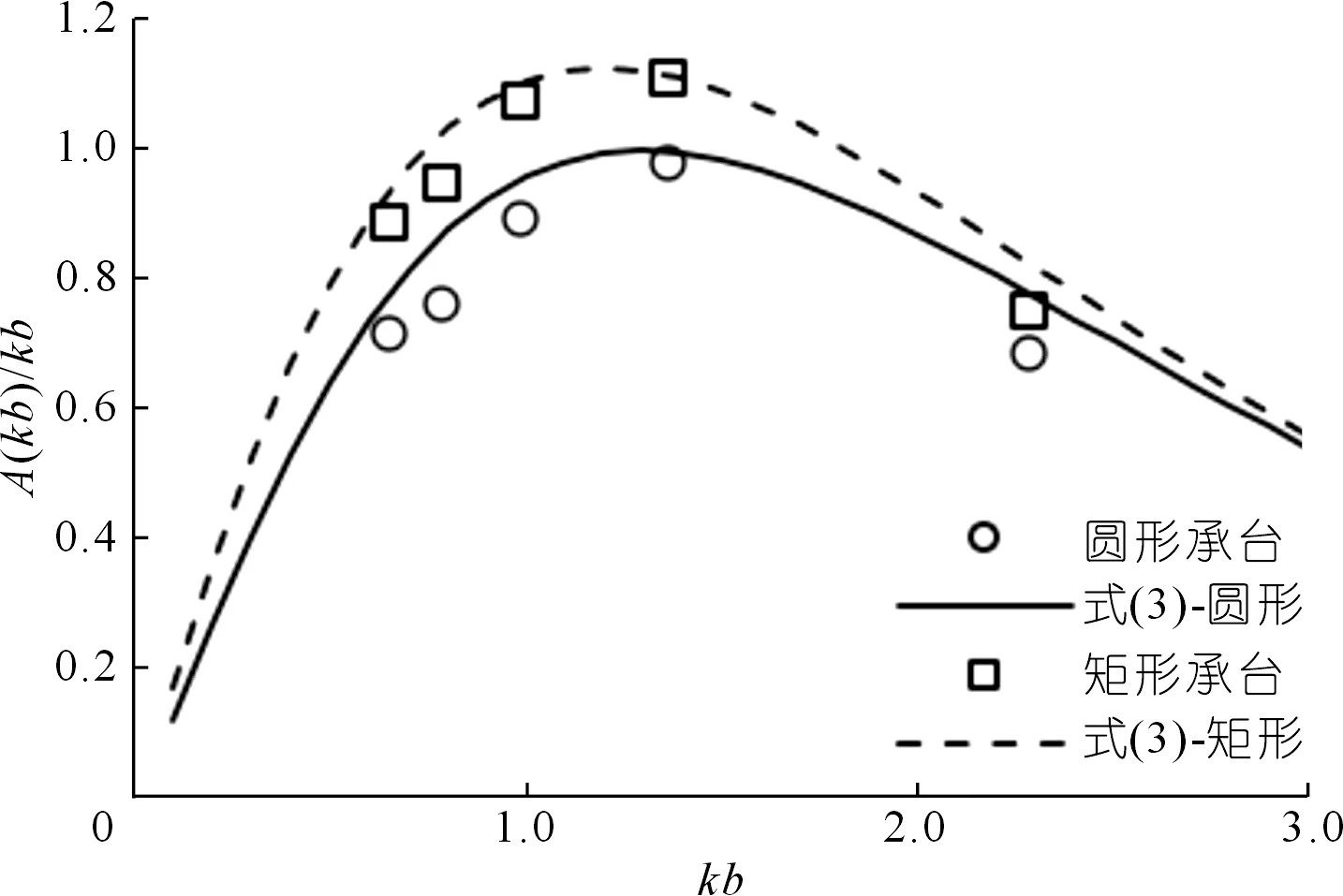
圖5 矩、圓形承臺A(kb)/kb隨kb變化規律

研究發現,當式(3)中α=2.6、β=1.3,圓形承臺數值計算的水平方向波浪荷載和式(2)計算結果基本一致。同時,采用Garrett[19]研究成果和式(2)計算結果進行對比驗證,如圖6所示,式(2)計算結果和Garrett研究成果吻合較好,差異基本在±15%以內。

根據Froude-Krylov理論,計算出圓形承臺和矩形承臺水平荷載比值K為

(5)

假定矩形承臺和圓形承臺波浪繞射系數相同,則圓形承臺和矩形承臺水平荷載比值K為

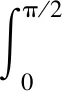
(6)

將比值K隨kb變化關系繪制于圖7,從圖中可以看出,式(3)、式(6)和數值計算結果均表明,在本文研究范圍內,隨著kb增加,比值K逐漸減小。當kb為0.5～1.5時,式(3)和式(6)計算結果均與數值計算結果基本接近,比值K基本在1.15～1.25之間;隨著kb增加,式(6)計算的K值減小較快,與數值計算結果差異較大,但式(3)計算結果與數值計算結果基本一致。

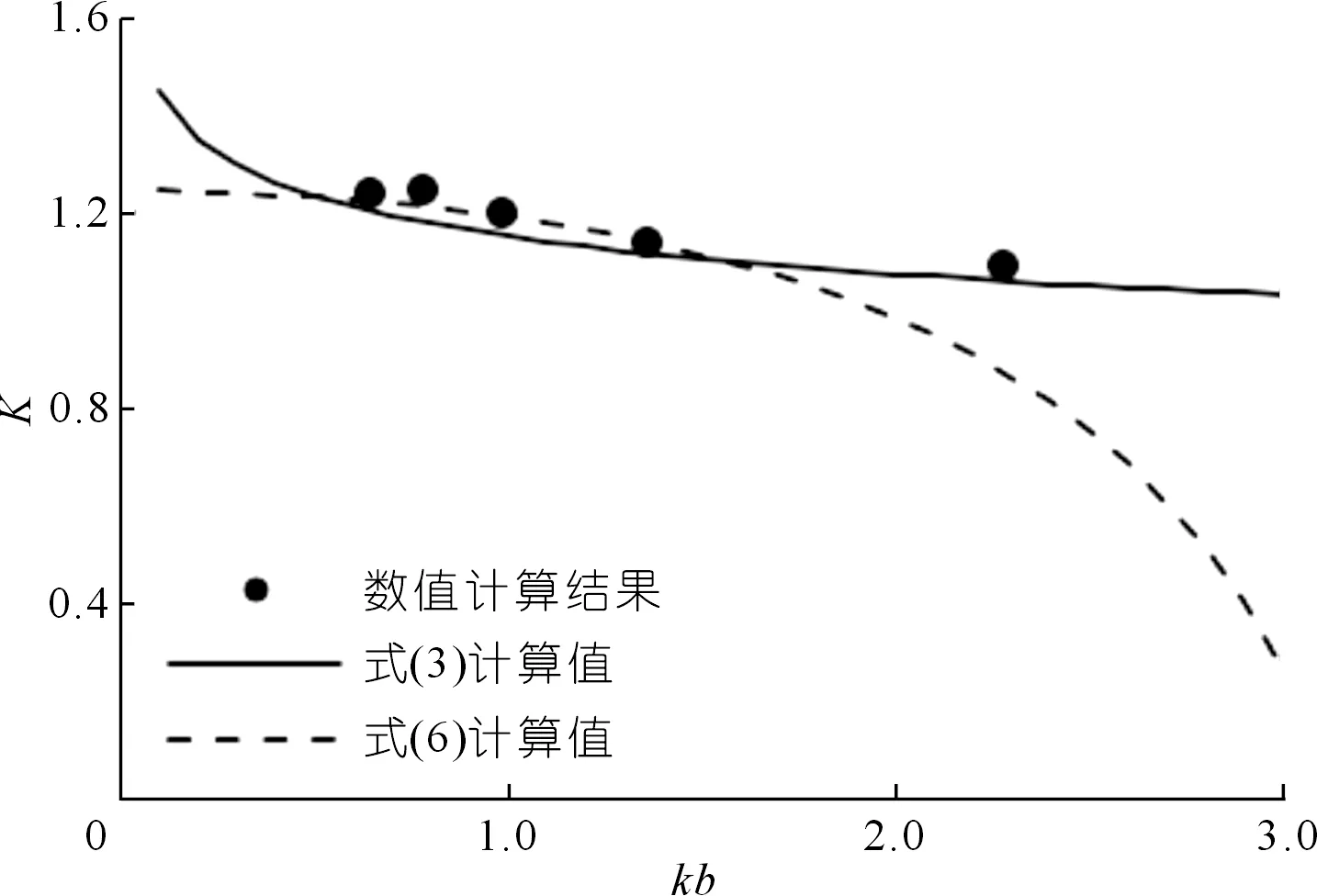
圖7 矩形承臺和圓形承臺水平方向波浪荷載比值

4.3 流速對承臺水平方向波浪荷載影響

波高H=2 m時,將不同流速(U為0,1,2,3 m/s)和周期條件下的矩形承臺水平方向波浪荷載及其對應的A(kb)/kb值繪制于圖8中。從圖中可以看出,隨著流速的增加承臺水平荷載也在增加,不同流速下A(kb)/kb隨kb變化規律和無流速時類似,均先增后減,通過修改式(3)中α和β值,式(3)也將適用。由于流速增加后波長變長,kb值減小,所以A(kb)/kb最大值對應的kb值有所減小。

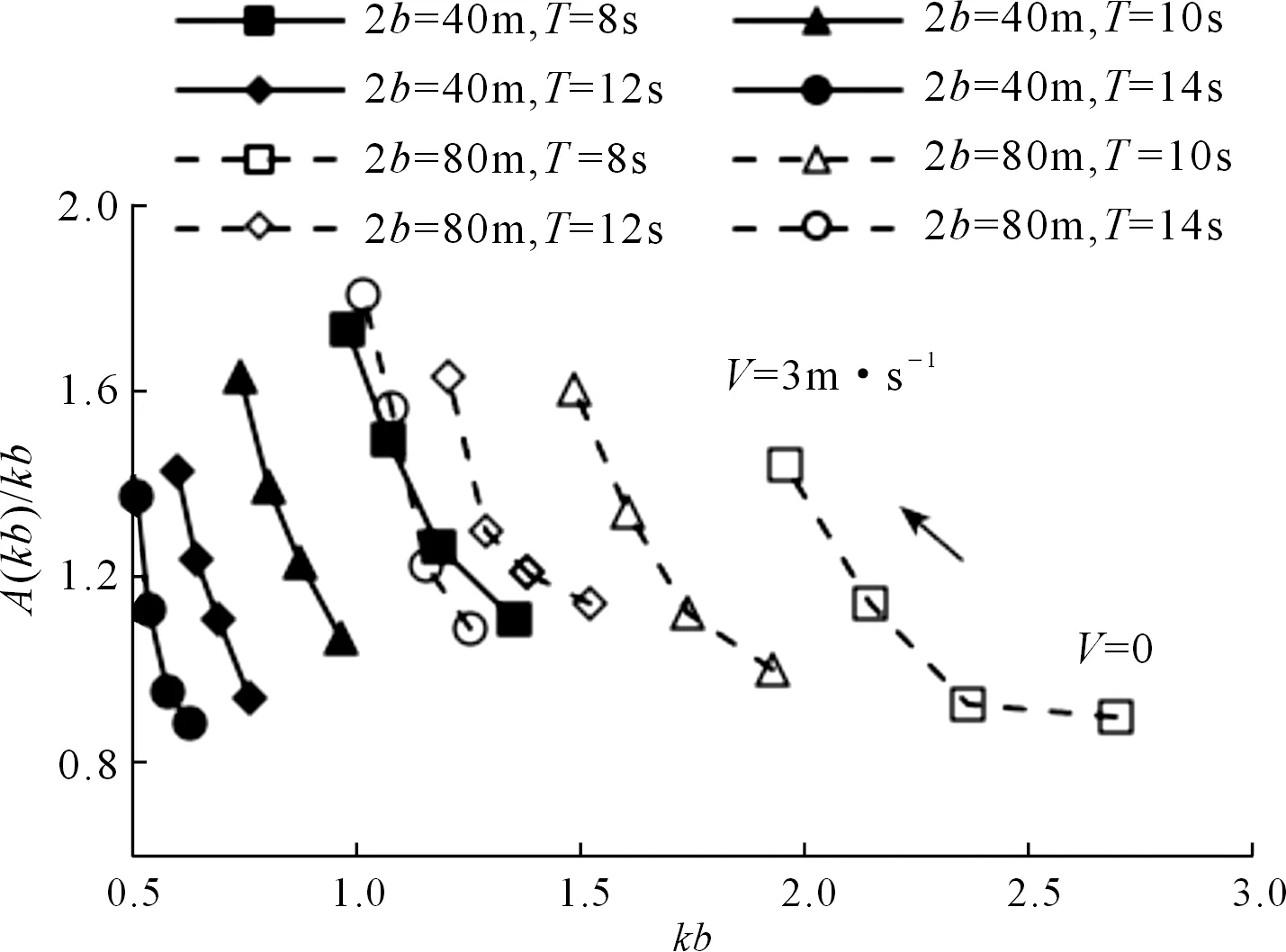
圖8 不同流速下A(kb)/kb隨kb的變化規律

5 結 論

(1) 參考杭州灣海域波浪特性和跨海橋梁承臺結構尺寸特征,建立了橋墩承臺數值波浪水槽模型,并根據波浪繞射理論,提出了考慮多因素的承臺水平方向波浪荷載計算方法,該方法能夠快速方便地計算出承臺水平方向最大波浪荷載。

(2) 由于矩形承臺對波浪阻礙作用大于圓形承臺,矩形承臺水平方向波浪荷載大于圓形承臺,當kb為0.5～1.5時,矩形承臺水平方向波浪荷載基本是圓形承臺的1.15～1.25倍,通過修改式(3)中α和β值后,計算方法同樣適用于不同形狀承臺水平方向波浪荷載計算。

(3) 承臺水平方向波浪荷載基本隨著流速增加逐漸增大,承臺水平方向波浪荷載隨kb的變化規律與純波情況相近,流速增加導致承臺相對長度kb變小,最大水平方向波浪荷載對應的kb值也減小。