基于Sentinel-2的川西高原植被葉片含水量反演

謝 兵,楊 武 年,楊 鑫,王 芳

(1.四川司法警官職業學院,四川 德陽 618000; 2.成都理工大學 地球科學學院,四川 成都 610059; 3.內江師范學院 地理與資源科學學院,四川 內江 641000)

0 引 言

葉片含水量的多少是植被長勢好壞的重要參考因素,也是植被蒸騰和固碳的主要因素,在植被生長過程中起到重要作用,進而對生態環境也有著重要的影響。對植被葉片水含量的廣泛監測,可以為植被生長狀況提供及時的科學評判,保證植被的良好生長。植被葉片含水量的多少對森林火災預防和減弱也有著重要的作用,植被葉片水含量越多植被燃燒的速度會越慢,植被著火點的溫度也會越高,有助于延緩森林火災和火勢蔓延,為及時撲滅火災贏得寶貴的時間[1]。

對于植被葉片含水量的測量或估算的傳統方法,往往都是將研究區劃分為眾多小區域,通過實地調查采樣和插值的方法得到整個研究區植被葉片含水量。衛星遙感可以大范圍、快速和多譜段地進行遙測,獲取大量地面上有效信息[2-3],具有高效、無損、低成本、覆蓋范圍廣等特點。通過遙感技術獲取植被葉片含水量主要有以下2種方法。

一是采用相應的輻射傳輸模型通過輸入不同的葉片結構參數、生化組分含量信息、入射光線最大入射角等定量反演植被冠層含水量。阿布都瓦斯提·吾拉木等[4]根據葉片和冠層輻射傳輸模型Prospect模型、Lillesaeter模型、Sail H模型、大氣傳輸6S模型構建了一種新植被指數SPSI(短波紅外垂直失水指數)來估算植被冠層含水量,并與野外實際測量的冠層含水量比較,研究發現兩者結果較為接近,新植被指數能很好地估算冠層含水量。程曉娟等[5]依據物理PROSAIL模型分析了對小麥冠層水分敏感的波段,利用這些敏感波段構建了一種新的植被水分指數,發現這種新植被指數對冬小麥冠層水分含量估算精度很高。

二是基于統計分析方法監測植被水分。Zhang等[6]利用了10個與水分相關的植被指數來估算冠層含水量(CWC)和冠層平均葉片等效水厚度(EWT),發現綠葉綠素指數、紅邊葉綠素指數、紅邊歸一化比值對CWC和EWT最為敏感。張海威等[7]通過分析8種植被指數與植被葉片含水量之間的相關關系,發現MSI和GVMI植被指數與植被葉片相對含水量的非線性三次擬合函數精度最高,GVMI指數反演的誤差最小。李玉霞等[8]基于光譜指數法建立植被含水量之間的關系模型,發現光譜指數法反演精度較高。

Sentinel-2衛星搭載的多光譜成像儀有13個光譜波段,其特有的植被紅邊波段在植被參數反演中有著重要作用,且與其他波段相關系數較低,提高了影像的光譜信息量,為影像分類提供了更多的光譜特征。本文基于Sentinel-2,提取6種植被指數,利用野外實測的60個樣本數據計算的葉片含水量數據,建立植被葉片含水量與植被指數之間的關系模型,并進行驗證,得到川西高原研究區植被葉片含水量分布結果,該結果對于四川地區的生態環境評價有著重要意義。

1 研究區概況與數據

1.1 研究區概況

松潘縣位于川西高原東北角,境內有大片森林覆蓋,適合作為研究區分析研究植被水含量。研究區主要包含松潘縣燕云鄉、紅扎鄉、小姓鄉、大姓鄉、安宏鄉、青云鄉、牟尼鄉等鄉鎮,總面積約1 000 km2,研究區內有兩條大的河流——熱務曲河和岷江,兩條河流匯聚于鎮江關鄉,年平均氣溫5.7 ℃,年均降水量720 mm,屬川西北高原氣候[9],研究區地理位置見圖1。

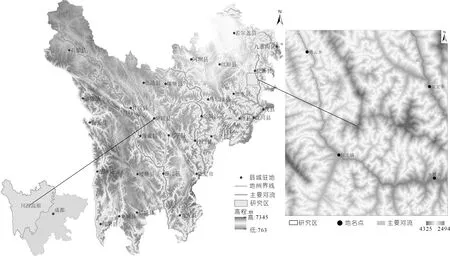
圖1 研究區位置

1.2 數 據

1.2.1葉片含水量測定

通過2018年8月進行的野外實地調查,在研究區內大致均勻設置60個樣方(見圖2)。主要記錄每個樣方的經緯度信息、高程、采集樹葉樣本。每個樣方內按照植被頂、中、底3層各采集10片樹葉現場采用經過校準的幸運JA303P型號電子分析天平稱其鮮重,采集的樹葉裝入紙袋中[10],采用葉面積測量儀測量樹葉面積。室內葉片樣品在70 ℃烘干24 h以上,直至恒重后再采用華志HZY-A400型號電子分析天平稱重葉片干重,按照公式(1)計算葉片含水量(以葉片等效水厚度表示)。

注:底圖為2018年8月Sentinel-2衛星影像,R:Band 8,G:Band 3,B:Band 2假彩色合成。

(1)

式中:EWTleaf表示葉片含水量,g/cm2;Wfresh表示新鮮葉片的重量;Wdry表示烘干后葉片的重量;A表示葉片的面積。

1.2.2遙感數據處理

Sentinel-2數據由于傳感器平臺在運行過程中的復雜情況,以及受到地球大氣情況、地表高程起伏狀態的影響,傳感器記錄的值往往與目標輻射亮度或地表反射率存在著偏差,需要通過數據預處理消除這些誤差[11]。經遙感數據預處理得到Sentinel-2地表反射率數據產品(見圖3)。

2 模型與方法

2.1 植被指數

植被指數常用來估算植被相關信息,常見的植被指數有NDVI、NDWI、TVI、FVC等,由于Sentinel-2數據是唯一一個在紅邊范圍含有3個波段的數據[12-14],增加了紅邊歸一化植被指數NDVI705,選取的植被指數見表1。

表1 Sentinel-2數據的植被指數計算公式

2.2 方 法

根據植被指數與葉片含水量的關系建立相應數學模型,方法包括:多元逐步回歸、隨機森林、BP神經網絡[15]。

2.2.1多元逐步回歸

多元逐步線性回歸是從所有變量中考慮與植被葉片含水量決定系數最大、均方根誤差最小的變量,直至所選取的模型效果最好的變量即為最優的變量。

多元回歸方程是假設有多個植被指數作為自變量x1,x2,x3…xn,它們與植被葉片含水量y之間存在如下關系:

y=a0+a1x1+a2x2+…+anxn

(2)

式中:a0為常數項,a1,a2,a3,…,an為待求回歸系數。

2.2.2隨機森林

隨機森林(Random Forest)是一種集成學習(Ensemble Learning)方法,通過集成多個決策樹來完成預測和分類任務。它結合了決策樹的特點和隨機性,具有較強的預測能力和穩定性。

設定不同葉子數和樹數,通過比較回歸得到的各種葉子大小和樹的數量的均方誤差來尋找最佳葉子大小和樹的數量(見圖4),從圖4中可以看出,葉子數為5、樹的數量為450時,誤差最小且穩定,利用該參數進行植被指數的重要性分析,重要性由大到小依次為FVC、NDVI705、NDVI、NDWI1,NDWI2、TVI。

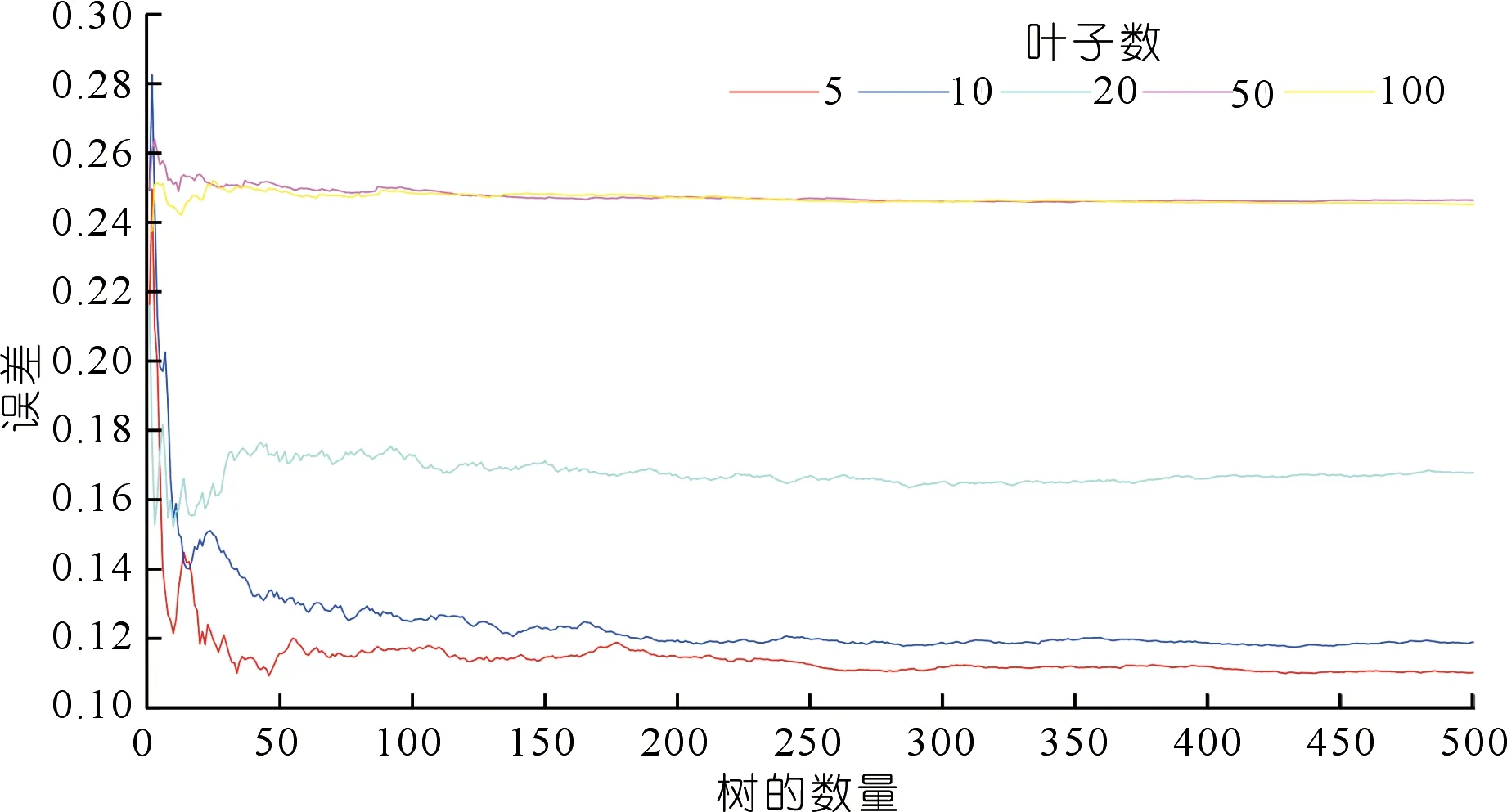
圖4 葉子數、樹數與誤差

2.2.3BP神經網絡方法

BP神經網絡能夠很好的處理輸入與輸出數據,主要由輸入層、隱藏層、輸出層3部分組成,輸入層與隱藏層和隱藏層與輸出層通過權重、函數進行連接,輸出層在隱含層的基礎上確定輸入變量和激活函數輸出,當與目標存在誤差的情況下,經輸出值與期望值比較,當誤差大于設定值時,則誤差反向傳播,通過逐層修改神經元的權值,減少誤差,如此循環直到輸出的結果符合精度要求為止。

神經網絡隱含層的第i個節點的輸入變量neti為

(3)

隱含層的第i個節點的輸出變量為

yi=f(neti)

(4)

式中:f為激活函數,f(x)=1/(1+e-x),xj為隱含層第j個節點的輸入參數,wij為隱含層的第i個節點到輸入層的第j個節點之間的神經網絡權值函數。bi為閾值參數[16]。

隱含層神經元個數采用如下經驗公式確定:

(5)

式中:m為輸入層個數,n為輸出層個數。計算出本模型的隱藏層神經元個數為5。

2.3 精度評價方法

采用十折交叉驗證法的均方根誤差RMSE、平均絕對誤差百分比MAPE檢驗模型的精度,公式為

(6)

(7)

3 植被葉片含水量反演

3.1 因子相關性分析

采用的植被指數有6種,需要分析他們之間的自相關性,避免數據冗余,論文采用Pearson相關系數來確定植被指數之間的相關性[18](見表2)。統計學認為系數值的范圍在0～0.19之間為極低相關,0.20～0.39之間為低度相關,0.40～0.69為中度相關,0.70～0.89為高度相關,0.90～1.00為極高相關。

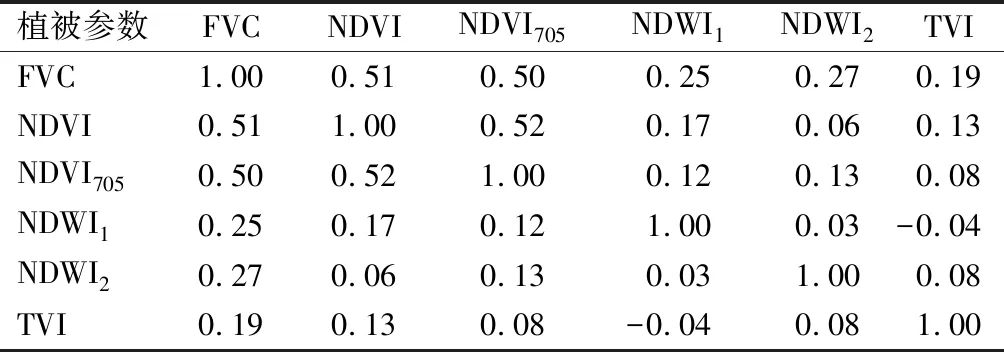
表2 植被參數之間相關系數

從表2可以看出,最大相關性為NDVI與NDVI705,Pearson相關系數為0.52;最小為TVI與NDWI1,Pearson相關系數為-0.04。只有NDVI與FVC、NDVI705與FVC、NDVI705與NDVI的Pearson相關系數處在中度相關,其他全部在極低度相關和低度相關,綜合分析,6種植被指數均可作為模型輸入數據。

3.2 植被葉片含水量反演模型與驗證

論文基于多元逐步回歸、隨機森林、BP神經網絡方法建立植被指數與植被葉片含水量遙感估算模型,并采用精度評價方法對3種模型加以驗證。根據十折交叉驗證方法,將60個樣本數據平均分成10份,其中9份用于訓練,1份用于測試。論文采用MATLAB軟件處理,運用crossvalind函數進行十折劃分,通過循環訓練計算10折交叉驗證的平均均方根誤差RMSE和平均絕對誤差百分比MAPE,結果見表3。

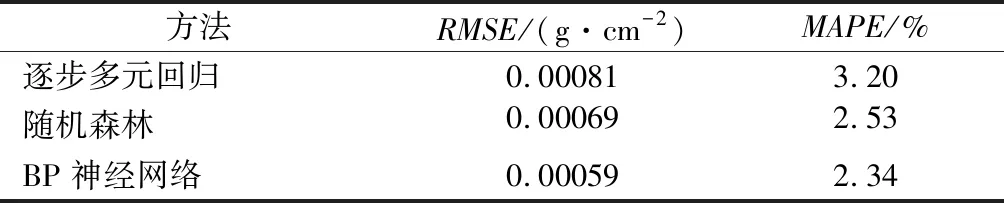
表3 十折交叉驗證法結果

從表3中可以看出,BP神經網絡在均方根誤差和平均絕對誤差百分比上均小于隨機森林算法和逐步多元回歸算法,分別為0.000 59 g/cm2和2.34%,可以認為3種方法中BP神經網絡模型反演植被葉片含水量效果最好。

3.3 植被葉片含水量反演結果

由于BP神經網絡模型在訓練數據和驗證數據集上精度最高,論文采用MATLAB軟件將Sentinel-2提取的FVC、NDVI、NDVI705、NDWI1、NDWI2、TVI植被指數作為輸入數據,運用已訓練好的BP神經網絡模型反演研究區植被葉片含水量,結果如圖5所示。

圖5 研究區植被葉片含水量分布

與圖1比較,可以看出河流段、城鎮村莊處呈現紅色,植被區域呈現綠色和黃色,河流、城鎮區域植被葉片含水量低,與實際情況一致。

4 結 論

本次研究從Sentinel-2影像和研究區實測葉片含水量為數據源,分析了Sentinel-2影像FVC、NDVI、NDVI705、NDWI1、NDWI2、TVI 6種植被指數,并對6種植被指數的相關性進行分析,通過多元逐步回歸方法、隨機森林方法與BP神經網絡模型,實現對川西高原植被葉片含水量的定量反演。結果表明:

(1) 基于因子相關分析,6種植被參數之間的自相關性低,均可以作為模型輸入參數。

(2) 采用隨機森林算法通過對葉片含水量與植被指數進行重要性分析,重要性由大到小依次為FVC、NDVI705、NDV1、NDWI1,NDWI2、TVI。

(3) 通過十折交叉驗證方法對3個模型進行評價可知,BP神經網絡均方根誤差和平均絕對誤差百分比最小,分別為0.000 59 g/cm2和2.34%,表明BP神經網絡模型優于逐步多元回歸模型和隨機森林模型。