高拱壩澆筑條帶協同的纜機群智能配置模型

趙春菊，閆楷文，劉 全，王 放，周華維

（1. 三峽大學水利與環境學院，湖北 宜昌 443002； 2. 三峽大學湖北省水電工程施工與管理重點實驗室，湖北 宜昌 443002；3. 湖北工業大學土木建筑與環境學院，湖北 武漢 430072； 4. 武漢大學水利水電學院，湖北 武漢 430072）

0 引 言

混凝土拱壩超載能力強、安全性高，適于高山峽谷水資源開發［1-3］。纜索式起重機具有起重量大、覆蓋范圍廣、機動性好等特點，可以橫跨峽谷和河流等復雜地形，適用于高拱壩的混凝土澆筑［4，5］。為了高效施工，往往配置多臺纜機組成纜機群澆筑大壩，小灣、溪洛渡、白鶴灘等拱壩的纜機臺數均達到4 臺以上［6-9］。

為了提高纜機群澆筑效率，通常利用多臺纜機同時澆筑多個澆筑倉。此時，不同澆筑倉的混凝土運距不同，各臺纜機的控制寬度不同，導致纜機之間吊運效率各異，進而造成澆筑循環時間和坯層覆蓋時間差異，難以保證澆筑條帶協同上升。加上纜機群共享軌道、塔架寬度和安全距離等因素的限制，纜機之間無法重疊和跨越，澆筑循環時間的差異可能會降低纜機的利用率，不利于纜機群發揮最大效能。因此，在多對多的纜機-澆筑倉優化配置問題中，期望各臺纜機控制區域內的混凝土覆蓋時間大致均衡，實現澆筑條帶的協同上升和纜機群同步移位，對于提高施工效率意義重大。

近年來，已有眾多國內外學者對拱壩澆筑中纜機配置優化的問題進行研究。王仁超等［10］構建了考慮空間沖突的纜機配置模型，為優化混凝土澆筑方案提供了依據。郭曉峰［11］從兩倉聯合澆筑的角度，根據優化目標，界定約束條件，提出纜機配置方案優選方法。王樹強等［12］基于纜機群高低線協同控制系統，優化了纜機群調度配置。黃建文等［13］根據高拱壩施工數據分析結果及排隊模型計算得到相關參數并建立目標模型，同時聯合纜機群安全運行的邊界方程取得最優的纜機配置。楊忠加等［14］基于高拱壩壩體生長特征與纜機配置之間的關系，優化了澆筑方案，提高了纜機的利用率。張志豪等［15］基于實時監控系統，通過定點下料的施工方法對纜機吊運混凝土的配置進行優化。在上述已有研究中對纜機優化配置在纜機之間作業干擾與聯合、纜機施工數據分析結果、基于拱壩壩體生長特征以及倉面定點下料等方面取得成果，對于提高纜機群的安全高效運行具有重要意義。然而，在已有的研究中尚未考慮各臺纜機的負載和澆筑循環時間差異對纜機群整體的施工效率的影響，因此有必要對纜機群的工作配置進行優化。

纜機群同時服務于多個澆筑倉時，單個澆筑倉又劃分多個澆筑條帶，按條帶配置纜機和倉面的平倉機、振搗機進行下料、平倉及振搗配套作業。顯然，纜機群與澆筑倉的匹配屬于典型的多對多動態組合問題。針對組合優化問題通常可以運用傳統算法進行求解，如0-x 算法［16］、線性規劃［17］、非線性規劃［18］、NSGA-II［19］、貪心算法［20］等算法。與普通的組合優化問題相比，纜機機動性強、服務組合方式靈活，僅從纜機和澆筑倉的層面進行澆筑組合遍歷，組合規律難以提取，屬于NP-Hard 在線裝箱難題［21］，且其解空間容量十分巨大，直接求取必然面對“維數災”，求解和優化非常困難。因此，復雜條件下考慮吊運負荷均衡的多纜機對多澆筑倉組合優化問題需要進一步研究。為此，本文提出一種“微匹配”的方法，將纜機覆蓋范圍與澆筑倉重疊的區域即澆筑條帶進行微分化處理，在澆筑倉的微分條帶內，纜機和條帶之間可簡化為一對一的關系，在此基礎上建立求解模型。

綜上所述，本文研究并提出了一種纜機群智能配置模型，以實現各纜機循環時間、負載比較均衡的優化目標。該模型首先對各纜機覆蓋范圍與澆筑倉重疊的區域進行澆筑條帶劃分，然后對澆筑條帶進行微分化，通過微條帶與微匹配建立纜機微條帶一對一的匹配關系，并且根據澆筑匹配中的邊界、約束條件和優化目標建立微匹配的積分表達實現纜機群與澆筑條帶組合的優化。結合白鶴灘工程的纜機優化配置方案驗證了本模型的可靠性和有效性

1 澆筑匹配模型

大壩澆筑過程可以看作是由纜機對澆筑倉服務逐步推動系統狀態變遷的過程。當配置不同澆筑方案時，系統所占用的入倉資源（如纜機數量）不同，消耗的澆筑時間不同，服務的倉位不同，得到的壩體澆筑面貌也不同。因此，澆筑方案優化是大壩施工過程優化的核心。

實現澆筑方案優化需要先求解可選澆筑方案集，再根據優化目標從中選擇執行方案。

設：可選澆筑方案PM即是入倉資源與澆筑倉之間的匹配關系，在本文中特指多臺纜機與多澆筑倉的組合關系。可用纜機集{CC}和擬澆倉位集{Blk}的組合表示，如式（1）：

式中：CC參與澆筑的纜機；Blk為澆筑倉位。

某時刻四臺纜機{CC1，CC2，CC3，CC4}澆筑兩個倉位{Blk0，Blkk}以及所劃分澆筑條帶集合{Rng1，Rng2，Rng3，Rng4}的澆筑匹配如圖1 所示。可見，澆筑匹配PM可用澆筑矩陣表示，矩陣中的匹配元記為pm，表示具體的纜機與澆筑倉的匹配，如圖2所示。

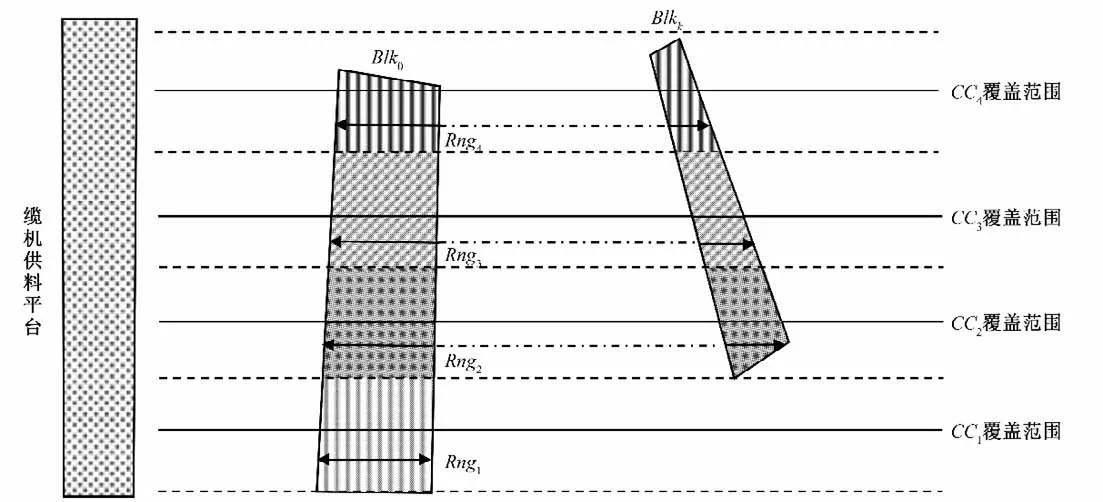
圖1 某CC和Blk的澆筑匹配示意圖Fig.1 Match of pouring diagram of a CC and Blk

圖2 某CC與Blk的匹配矩陣Fig.2 The matching matrix of some a CC and Blk

2 纜機智能配置模型

2.1 澆筑倉微條帶

某一時刻存在澆筑匹配PM，PM.Blk為該匹配中的澆筑倉，根據平移式纜機覆蓋的特點，將澆筑倉的纜機覆蓋范圍微分化為澆筑倉微條帶PM.Str，如圖3。

圖3 澆筑倉位及微條帶示意圖Fig.3 Schematic diagram of pouring blocks and micro strip

2.2 基于微匹配的澆筑組合優化流程

在圖3 中纜機覆蓋的澆筑倉面劃分的條帶進行微分化，可建立澆筑組合優化的微匹配積分表達，對澆筑倉存在式（2）的積分：

式中：dl為垂直于平移式纜機方向的長度微元。

將纜機和條帶多對多關系，通過微條帶和微匹配轉換為一對一關系，以便在微匹配層面處理澆筑組合優化問題，解法步驟見圖4。

圖4 微匹配的澆筑組合優化流程Fig.4 Micro match of pouring configuration optimization process

不失一般性，針對從澆倉位集Blk中提取倉位Blki，纜機集CC 中可選出某纜機CCm，根據其澆筑覆蓋條帶范圍CCm.Rng可得到CCm針對Blki內的一個條帶狀澆筑控制區域CCm.Blki.Rng，該纜機與該條帶即為一對一服務關系。但是，由于纜機的覆蓋條帶范圍受到眾多條件限制，難以統一。為便于處理均衡性等優化目標，將條帶范圍微分化，從微條帶Blki.Str積分的角度反映纜機的覆蓋關系。則澆筑微匹配組合可表達為式（3）：

2.3 澆筑匹配問題的基本施工約束

根據纜機澆筑作業規則，對于任一匹配組合存在施工邊界約束：

（1）纜機下覆的澆筑倉坯層層間覆蓋要求。根據各纜機覆蓋范圍內的面積、澆筑厚度和混凝土初凝時間，各纜機的澆筑強度需要滿足層間覆蓋需求。

（2）纜機群對澆筑區域的覆蓋完備性。在各澆筑倉上的所有微條帶必須保證在纜機群的覆蓋范圍內。

2.4 優化目標

纜機對澆筑倉的澆筑組合優化目標為：纜機群協同完成澆筑的時間短，各纜機間負載盡量均衡。

（1）纜機群澆筑的總澆筑強度最大。纜機對微條帶的澆筑覆蓋強度隨距離增大而減小，即纜機的循環時間會增長。為了盡快完成澆筑任務，總體上希望纜機群澆筑的總強度最大，循環時間優化目標的表達見式（4）。

式中：pmmCC為纜機m的匹配組合，pmmCC.Pwr為纜機m匹配組合中的總澆筑強度。

（2）纜機間的負載均衡。對各纜機而言，希望纜機間負載均衡，方便纜機間協調。負載均衡的優化目標表達見式（5）。

式中：var{pmmCC.Pwr}為纜機m匹配組合總澆筑強度的負載方差。

2.5 智能配置

在常態混凝土拱壩澆筑過程中，受河谷形狀、相鄰高差、壩身結構、澆筑資源等多因素影響，各壩段交錯上升，澆筑倉的約束狀態隨之動態變化。當某一倉的澆筑作業開始或結束時，纜機資源的閑/忙狀態也隨之轉變。因此，在進行纜機澆筑作業匹配規劃時，可利用的纜機工作臺數與可澆筑倉的數量和空間分布關系隨時間動態變化。本模型在空間中對纜機群下覆面積進行空間微分/積分，動態匹配纜機與澆筑倉，在微觀上優化纜機與微條帶之間的組合關系；在宏觀上，實現纜機負載的均衡和纜機群高強度澆筑，充分利用纜機群的運輸能力來完成澆筑任務。通過建立的微匹配模型，拱壩仿真系統通過遍歷調整微匹配與纜機之間的組合關系來自適應動態變化的條件，利用迭代優化均衡纜機—微匹配—澆筑倉組合關系，均衡纜機之間負載，優化纜機群澆筑的總強度，實現纜機群智能配置。

3 案例研究

白鶴灘工程采用雙層布置的7 臺（4+3）平移式纜機澆筑。某時刻擬同時澆筑7、13、15 號壩段倉位如圖5。倉位基本信息如表1。針對7 臺纜機對3 個澆筑倉的組合優化問題。利用本文提出的纜機智能配置模型，可解算得到7、13、15 號壩段倉位及澆筑纜機群間的組合匹配關系，如圖5所示。

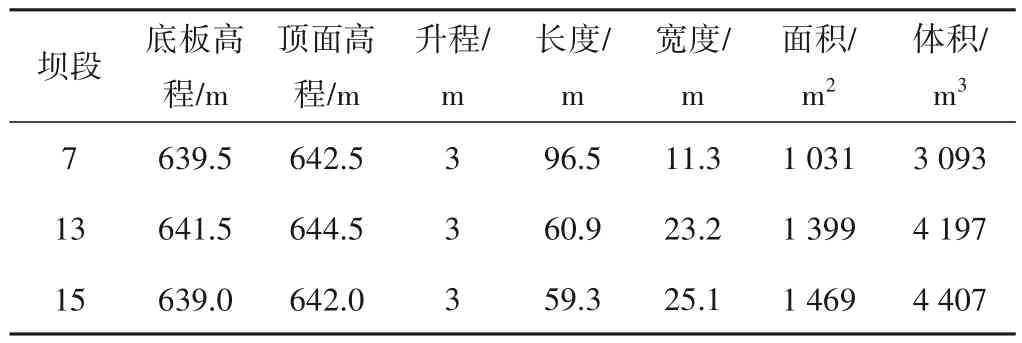
表1 案例壩段倉位基本信息Tab.1 bBsic specifications of dam blocks

圖5 壩段倉位空間位置及纜機集基本信息Fig.5 Spatial position of dam blocks and basic information of cable cranes

案例的覆蓋澆筑組合矩陣見圖6，基于纜機群智能調配模型解算得到各纜機覆蓋澆筑條帶的澆筑強度如圖7，各纜機覆蓋的澆筑倉面積如圖8。

圖6 案例的覆蓋澆筑組合矩陣Fig.6 The coverage pouring configuration matrix of the case

圖7 纜機壩段倉位對應澆筑強度Fig.7 The position of the cable dam blocks corresponds to the pouring strength

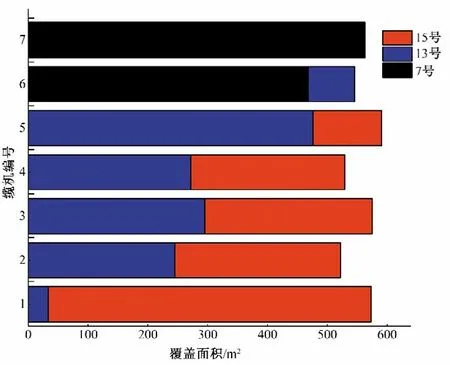
圖8 纜機壩段倉位對應覆蓋面積Fig.8 Corresponding coverage area of cable crane dam section

由圖7、圖8 可知，根據澆筑強度與覆蓋面積可以得到纜機的作業時間。纜機1～7 號對其覆蓋的面積下澆筑強度基本接近，經過計算1～7 號纜機的平均澆筑強度為69.9 m3/h。進而可以計算得到1-7號纜機基于平均澆筑強度偏差，如表2所示。

表2 各纜機的作業時間和強度偏差Tab.2 Cycle time and strength deviation of each cable crane

由表2可知，各纜機的作業時間基本均衡，說明各纜機覆蓋的面積與其所覆蓋的澆筑條帶范圍內的澆筑強度基本保持均衡，即保證了澆筑條帶的協同上升。1、3、5、7 號纜機同為下層纜機且澆筑強度偏差均為5.1%，2，4，6 號纜機同為上層纜機且澆筑強度偏差均為-6.8%，1、3、5、7 號纜機與2，4，6 號纜機分屬不同的平臺，且分配的條帶尺寸也稍有差異，故澆筑強度偏差不同，但是同平臺的纜機負載均衡，且上下平臺的偏差量基本接近，可以實現纜機群的同步移位，提高澆筑效率和保證施工安全。

綜上所述，本模型對纜機群的調配實現了循環時間和負載的優化目標。在倉面條帶范圍內，各纜機可以實現協同上升、同步移位。實例證明本文模型具有良好的穩定性和實用性，對纜機群和澆筑倉進行了較好的配置。

4 結 論

考慮澆筑條帶間纜機協同澆筑和上升，建立纜機群澆筑的智能調配模型，并運用在白鶴灘拱壩澆筑仿真中，得到以下結論。

（1）提出基于微匹配的澆筑組合優化模型。通過引入微匹配將纜機和澆筑倉條帶之間多對多關系轉換為纜機和微條帶之間的一對一關系；進而建立基于微匹配的澆筑組合的積分式，表達纜機群總強度和負載均衡的優化目標，構建了纜機群澆筑的智能配置模型，利用迭代優化求解。

（2）本文建立的纜機群和倉位澆筑組合優化模型，在白鶴灘等工程的澆筑施工仿真中運用取得了良好的優化效果。對可變數量的纜機同時澆筑多個澆筑倉的復雜情況，具有較好的求解適應性和穩定性。在拱壩施工數字孿生系統中，可預測拱壩澆筑歷時，并可作為纜機群澆筑活動的數值分析核心。