豐富體驗，把握本質，培養量感
——以“認識面積單位”教學為例

江蘇省無錫市新吳區泰伯實驗小學 毛 蓉

新課標把“量感”作為核心素養的主要表現之一，指出量感主要是指對事物的可測量屬性及大小關系的直觀感受。如何在小學階段培養學生的量感呢？本文以“認識面積單位”的教學為例，談談培養學生量感的一些策略。

一、構建生活場景，豐富感知

生活情境是培養學生量感的重要場所，教師可有意識地構建生活場景，滲透“量”的知識，喚醒學生的感知，幫助學生理解概念、記錄感受、培養對“量”的直覺。如在“認識面積單位”的學習中，教師就可以構建多樣化的學習場景，讓學生在豐富的表象中，鍛煉量感的眼光。首先，創設豐富的實物場景。為了讓“1平方厘米、1平方分米、1平方米”這些面積單位可看、可感、可估、可測，教師可準備豐富的實物與圖片，如邊長為1厘米的方格圖、棱長為1分米的禮物盒、邊長為1米的學習園地等。教師也可以在著裝上精心準備，配備的襯衣紐扣等都是大約1平方厘米大小的正方形，這些與標準單位接近的實物隨處可見，讓學生隨時參照、比較、記憶，幫助學生建立概念，培養學生用量感的眼光觀察身邊的事物。其次，準備充分的教具、學具。生活場景中的實物大多是非標準單位，為了形成更加精準的感知覺，教師還要做好充分的教具和學具準備，即提供精準的面積單位，如1平方厘米和1平方分米的紙片、四把米尺等，通過標準單位與實物相比較，引導學生不斷修正自身的認識，鍛煉敏銳的量感思維。

二、創設真實情境，體會創造

量感培養的重點不在于在已知測量單位后進行測量，而是讓學生能夠識別出量的屬性，并“創造”或選擇合適的度量單位進行量化。可見，讓學生經歷度量單位的產生過程非常重要。在“認識面積單位”的教學中，教師創設真實情境，通過三次比較面積大小，引出統一度量單位的需求，激發學生自主創造面積單位。

【設計片段1】

1.直觀比較

比較下面兩個長方形面積的大小。（見圖1）

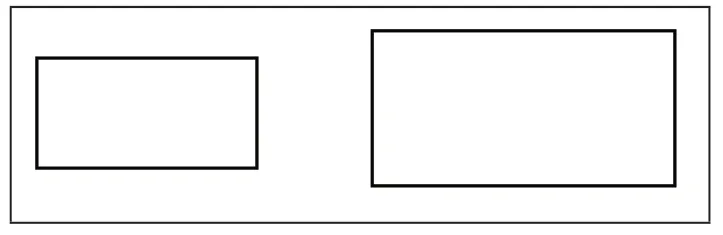
圖1

說明：通過觀察，我們能一眼看出兩個長方形的大小。

2.“小方格”比較

怎樣比較下面兩個長方形面積的大小呢？（見圖2）

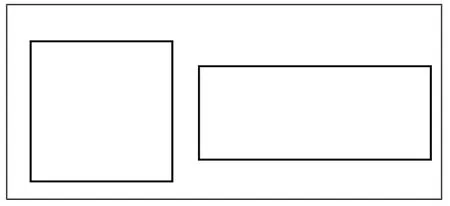
圖2

引導：當采用觀察法、重疊法無法比較時，怎么辦？說明：可以放在方格紙上比一比。

3.激活統一度量單位需求

情境：還有兩個長方形藏起來了，聽聽它們是怎么說的吧。

播放錄音：1號長方形有16個小方格那么大，2號長方形有36個小方格那么大。猜猜看，誰的面積大？（見圖3）

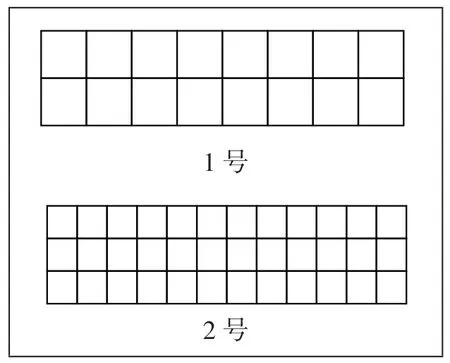
圖3

引導：通過重疊，我們發現這兩個長方形的面積是相等的。為什么方格數不同，面積卻相等呢？

說明：用大小不同的方格去測量面積，難以得到正確的答案，我們需要統一方格的大小。這個統一規定的方格大小，就是面積單位。

4.創造面積單位

師：數學上會用邊長為多少的方格作為面積單位呢？

生：邊長1厘米的方格、邊長1分米的方格、邊長1米的方格等。

在上面的環節，教師創設情境，引導學生經歷多樣化的比較過程，從直觀的觀察法、重疊法，到產生“小方格”需求的非標準單位比較，再在比較結果與猜測沖突中，產生統一小方格大小的需求，創造出面積的標準度量單位。學生在真實情境中經歷多次選擇合適方法的度量比較，積累豐富的“度量”經驗，有利于建立標準單位的表象。

三、設計具身活動，強化體驗

對小學生而言，不與其主觀經驗產生聯系的知識，幾乎無法使其產生真正意義上的學習。教師在教學活動中要通過不同的形式，調動學生多種感官，讓學生主動參與其中，在動手操作、動腦思考中獲得對“量”的感受。如在“認識面積單位”的教學中，教師可設計以下環節。

【設計片段2】

1.找一找。數學上規定，邊長為1厘米的小方格就作為測量面積的一個單位。你能從學具框中找到它嗎？

2.畫一畫。你會在紙上試著畫出1平方厘米嗎？準備怎么畫？

3.記一記。把1平方厘米拿在手中看一看，閉上眼睛想一想1平方厘米有多大。

4.舉一舉。生活中哪些物體的面是1平方厘米呢？

5.估一估。這個長方形的面積是多少平方厘米？（見圖4）

圖4

你是怎樣估的？驗證一下。

出示圖5：

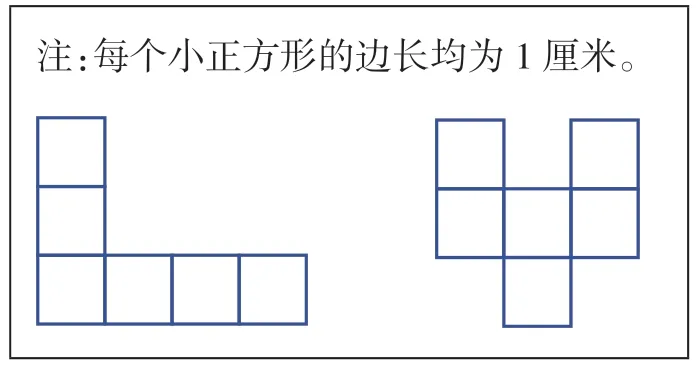
圖5

這兩個圖形的面積是多少？為什么它們的面積都是6平方厘米？

說明：看來只要包含幾個1平方厘米，就是幾平方厘米。

感官體驗是形成量感的基礎。在上面的環節，教師設計了大量的體驗活動，引導學生在觀察、觸摸、比較、估計等活動中經歷概念的形成過程，增強對“量”的敏感性，并逐步形成判斷推理的直覺。尤其在“估一估”環節，學生借助頭腦中建立的度量單位測量長方形的面積，在用的過程中加深了對面積單位的理解，在比較圖形面積的過程中，進一步體驗面積的本質，即面積單位的累加。

四、加強對比聯系，自主建構

比較是概念理解的重要策略。量感的發展需要對不同知識進行比較，在思辨、聯系、拓展中突出數學本質，系統建立知識結構。在“認識面積單位”的學習中，教師可加強兩方面的比較。

一是縱向對比。認識“平方厘米”“平方分米”“平方米”三個單位后，教師設計這樣一個環節：“你能把三個面積單位按大小排排隊嗎？”根據學生的回答，教師有意識地把三個面積單位重疊在一起，通過三個單位大小的直觀對比，加深量感的體驗。接著，教師進一步追問：“看著這三個面積單位，你有怎樣的猜想？有更大的面積單位嗎？”這一問題把學生的思維引向縱深處。學生通過知識遷移，自然地想到“平方毫米”“平方千米”等單位。在“排排隊”“猜一猜”等活動中，教師幫助學生把散點的知識串聯成知識的鏈條，在對比聯系中加深理解，在方法遷移中學會學習。

二是橫向對比。教師利用課件動態呈現點動成線、線動成面的過程，讓學生感悟點、線、面之間的關系。接著，教師出示1厘米和1平方厘米，啟發學生思考：“這兩個單位中都有厘米，它們有什么不同？又有什么聯系？”在對比中，學生清晰“1厘米”是長度單位，用來測量線段的長度，而“1平方厘米”是面積單位，用來表示面積大小。同時也感悟到兩個單位盡管不同，但面積單位的大小離不開長度單位的刻畫，它們在測量時都是通過單位的累加完成的，在數學本質上又有著相同之處。

縱橫對比，讓學生對概念的理解更加清晰。在多次比較中，學生整體建構知識網絡，發展量感素養。

五、開展主題實踐，深化拓展

量感的建立是一個從意識萌芽到相關知識學習，再到相關技能應用的過程。學生只有運用對“量”的理解，觀察生活，并通過推理、想象、比較，對生活中的“量”進行合理表達，才能內化為自己的能力和素養，真正做到心中有量、腦中有感。在“認識面積單位”的學習中，教師可設計主題實踐活動，讓學生在更加開放動態的時空中，獲得量感的新體驗。

（一）教室中的測量

1.量一量課桌面的面積。我們已經認識了“平方厘米”“平方分米”“平方米”三個面積單位，如果要測量課桌面的大小，選擇哪個單位比較合適？可以怎樣測量呢？同桌合作量一量。

學生活動后，交流不同的測量方法。

（1）滿鋪：用1平方分米的小正方形逐一鋪滿桌面，一共需要24個，所以，課桌面的面積是24平方分米。

（2）不滿鋪：只需要沿著長擺一排，需要6個，再沿著寬擺一擺，可以擺4個，說明有這樣的4行，這樣就可以算出一共有24個了。（見圖6）

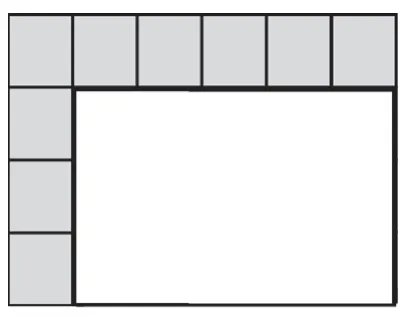
圖6

（3）直尺測量：我們用直尺就可以測量出來，先量出課桌的長有6分米，說明如果用1平方分米去擺，可以擺6個；再量出課桌寬是4分米，說明可以擺4排，最后用6×4=24就可以算出一共需要24個1平方分米，所以，課桌面的面積是24平方分米。

2.量一量教室地面的面積。測量教室地面的大小用哪個單位比較合適？你準備怎樣測量？

在經過課桌面的測量與交流后，學生一致認為不需要用1平方米的單位面積去測量，只需要量一量教室的長、寬，就能算出教室的面積。

測量是發展學生量感的重要載體。豐富的測量活動，有助于學生由感性的量感上升至理性的量感。在上述課桌面的測量過程中，學生由滿鋪測量，到不滿鋪測量，再到直尺測量，思維經過依賴經驗、化簡方法、抽象推理的過程，強化了量感的體驗，并為后續圖形面積公式的推導積累了經驗。

（二）眼力大比拼

1.估計圖中不規則圖形的面積是多少平方厘米？你是怎樣估計的？圖中正方形的面積呢？你又是怎樣想的？（見圖7）

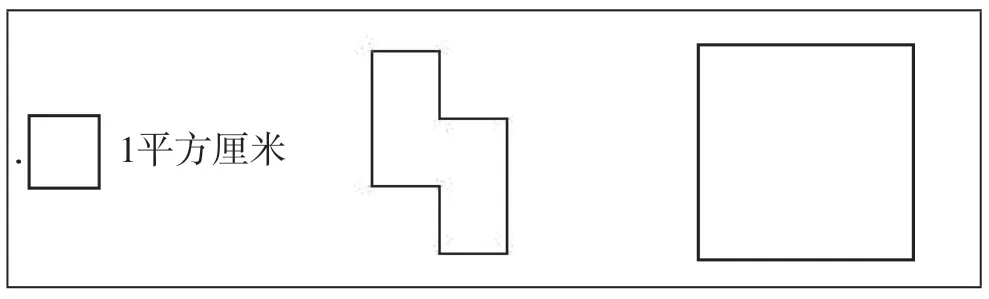
圖7

2.你能估計出一張撲克牌的大小嗎？你又是怎樣估計的？

3.你能估計出數學課本封面的大小嗎？比一比，看誰的眼光最準。

估測可以說是一種輸出表達，借助內在建立的標準，衡量比較具體的量的大小。學生在比較、表達、修正中，強化量感的認知，進一步體驗量的有限可加性。上面的活動層層推進，以1平方厘米為基準，估測不規則圖形和正方形的面積，在此基礎上估測一張撲克牌的大小，讓學生在一次次用數學的眼光觀察生活中，進一步精準“量”的感受。同時，教師有意識地滲透估測的方法，幫助學生建立不規則圖形與正方形、正方形與撲克牌、撲克牌與數學課本的聯系，引導學生通過疊加、推算，建立較大的量感參照值，從而進行更加合理準確的估測。

總之，學生量感的發展是一個不斷積累的過程。教師要把握“量”的本質，構建“量”的場景，組織豐富的“量”的活動，引導學生積累“量”的體驗，豐盈“量”的感知，真正讓量感從學生心底生長出來。