零序電流互感器配大電阻的配電網單相接地故障檢測
劉健,劉海,楊曉西,張志華
(1.西安科技大學 電氣與控制工程學院,西安 710054; 2.陜西省電力科學研究院,西安 710100)
0 引 言
單相接地故障是配電網中最常見的故障,在中性點非有效接地配電網單相接地故障檢測、選線和定位方面已經取得了大量研究成果[1-6]。
零序電流互感器(零序TA)是實現單相接地故障檢測的重要部件,其性能直接影響到故障處理效果。電力行業標準DL/T 866-2015《電流互感器和電壓互感器選擇及計算規程》對TA的參數選型及計算做出了規定。文獻[7-8]分析了保護用TA穩態和暫態傳變特性。文獻[9]討論了溫度對電子式TA和電磁式TA的影響。文獻[10]研究了開口式電流互感器的耐直流性能。文獻[11]研究了TA的建模方法。文獻[12]設計了實驗對零序電流過濾器的特性進行了分析。
已有成果均圍繞TA二次側阻抗較小的工況進行研究,而罕見針對TA二次側配置大負載電阻的情況下TA的特性及其應用的研究報道。實際工作中,經常在國外進口的智能開關的零序TA二次側觀察到有并聯較大負載電阻的現象,作者認為這種接法有應用于單相接地故障檢測的可能性,但是未見任何說明和解釋。
在單相接地故障處理中,檢測精度并非最終目的,識別出接地故障發生在區內還是區外,從而正確地選線和跳閘才是最終目的所在。零序TA二次側并聯較大電阻雖然有可能降低了其精度,但是卻可以放大二次側信號,尤其是在高阻接地導致一次側零序電流較小時,還有可能使其故障特征更加明顯,為單相接地檢測提供方便。另外,這種做法可以省去二次側電流互感器,使檢測電路更加簡單。
探討零序TA二次側配置大負載電阻時的特性,并以電力系統中占比超過70%的中性點不接地配電網為例,探討零序TA二次側配置大負載電阻的單相接地故障檢測方法的應用可行性。
1 零序電流互感器配大負載電阻時的特性
1.1 等效電路
零序TA等效電路如圖1所示,將一次側參數等效至二次側,一般情況下一次側繞組電阻和漏抗較小,折算至二次側時可忽略不計。圖中I0為零序TA一次零序電流;Is為二次電流;Im為勵磁電流;Kn為額定變比;Es為二次感應電勢;U2為負載電壓;Zm為勵磁阻抗;Z2為二次繞組阻抗;R為負載電阻。
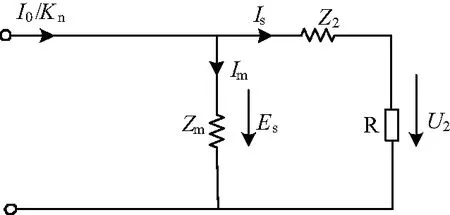
圖1 零序TA等效電路
零序TA基本變換式為:
I0/Kn=Is+Im
(1)
零序TA比值誤差εi為:
(2)
將式(1)兩邊同乘以R,聯立式(2),有:
(3)
式中Kn=N1/N2,N1和N2為一次和二次繞組匝數;I0、Is和Im均為均方根值。
當零序TA誤差較小時,其比值誤差εi和相角誤差δ的表達式可近似表示為:
sin(φ+θ0)×100%
(4)
cos(φ+θ0)×3440
(5)
式中μ為鐵芯磁導率;l為鐵芯平均磁路長度;Ac為鐵芯有效截面積;φ為二次回路阻抗角;θ0為損耗角;f為電源頻率。
通過式(4)和式(5)可知,當I0不變,R增大時,εi和δ增大,即鐵芯中勵磁電流增大,因此Es和U2增大,且由式(3)可知U2增大(1+εi)R倍。當R+Z2>>Zb,R>>Z2時,U2≈Es,φ≈0,Es與Is同相位。Zb為零序TA額定負載阻抗值。給出了此時TA向量圖,如圖2所示,Φ為鐵芯磁通。
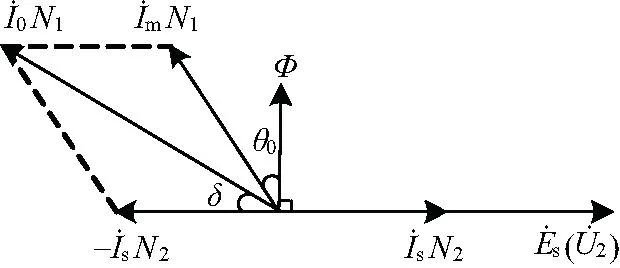
圖2 零序TA配大負載電阻向量圖
隨著負載電阻R的增大,零序TA的鐵芯會發生飽和現象,即鐵芯磁通飽和,U2不再變化。TA飽和后式(1)~式(3)依然成立,而式(4)和式(5)為零序TA誤差較小時的近似計算公式,因此式(4)和式(5)失效,此時εi需用式(3)計算,而δ則需通過實驗進行測量。
由于TA飽和后依然滿足電磁感應原理,因此,有:
(6)
其中:
B=μ(H+M)
(7)
Hl=N1im
(8)
聯立式(7)和式(8),有:
(9)
式中B為磁通密度;H為磁場強度;M為磁化強度;es為二次感應電勢瞬時值。由式(6)可知制約es的因素,即制約u2的因素,主要有Ac、N2和B;由式(9)可知B隨l減小而增大。因此在相同的使用條件下,二次繞組匝數更多、鐵芯有效截面積更大以及鐵芯平均磁路長度更小的零序TA,輸出的二次電壓信號更大。
為進一步研究增大R對零序TA傳變特性的影響,分析零序TA輸出特性,因此建立零序TA仿真模型,進行仿真分析。
1.2 仿真分析
基于Jiles-Atherton理論[13-14],對零序TA穩態傳變特性進行仿真。根據工程實際的典型值,TA取額定變比為150/5 A,額定二次容量Se為2 VA,二次繞組電阻為0.01 Ω,二次漏抗為0.02 mH。
考慮到發生高阻接地故障時故障電流只有幾百毫安,中性點不接地系統電容電流一般小于10 A,因此在仿真分析中,I0的取值范圍為0.5 A ~10 A。圖3給出了I0分別為0.5 A和10 A時,U2-R仿真曲線。
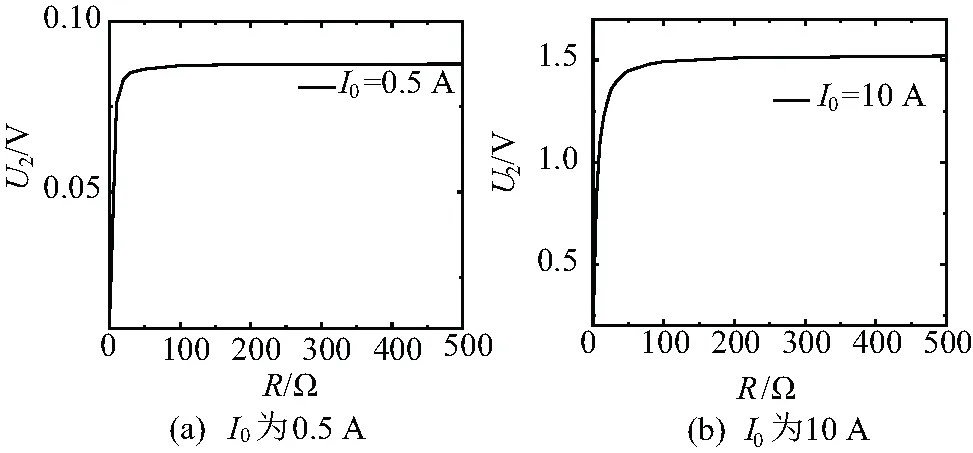
圖3 U2-R仿真曲線
由圖3可知,隨著R增大,U2逐漸增大,當R達到一定值后,U2呈飽和趨勢不再顯著增大。當I0為0.5 A,R約為50 Ω時,U2呈飽和趨勢;當I0為10 A,在R約為100 Ω時,U2呈飽和趨勢。為使得I0在0.5 A~10 A時,U2輸出值始終保持最大,TA二次側所配大電阻R的阻值應大于100 Ω。
為進一步分析不同R時,零序TA輸出特性,分別對R為1 Ω、12 Ω、122 Ω和200 Ω的情況進行仿真。圖4給出了I0小于20 A時,不同R對應的U2-I0仿真曲線。
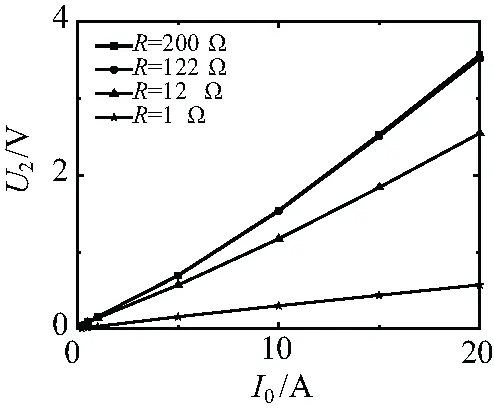
圖4 U2-I0仿真曲線
由圖4可知,隨著R增大曲線斜率也在增大,表明增大R使得零序TA的響應更加靈敏。但是隨著R的增大,曲線的非線性程度也逐漸增大,且122 Ω以上時對斜率的增大程度逐漸減弱,因此推薦采用100 Ω~122 Ω。
1.3 實驗驗證
以工程中常用的LXK-φ120型零序TA為例,搭建如圖5所示的零序TA輸出特性測試平臺進行實驗研究。被測零序TA變比為150/5 A,額定容量為2 VA,準確等級為5P10;電源為ONLLY系列微機型繼電保護測試系統,其每相輸出電流有效值為0~40 A。
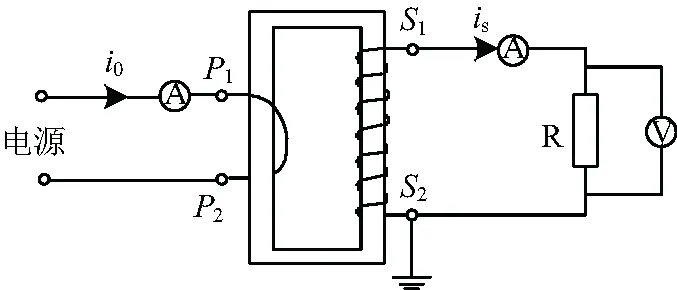
圖5 零序TA輸出特性測試實驗電路
實驗主要步驟:分別取R為1 Ω、12 Ω、122 Ω和200 Ω進行試驗,將一次電流從零開始緩慢增加至20 A,記錄對應的U2波形。圖6給出了不同I0和R時,U2的實測波形圖。
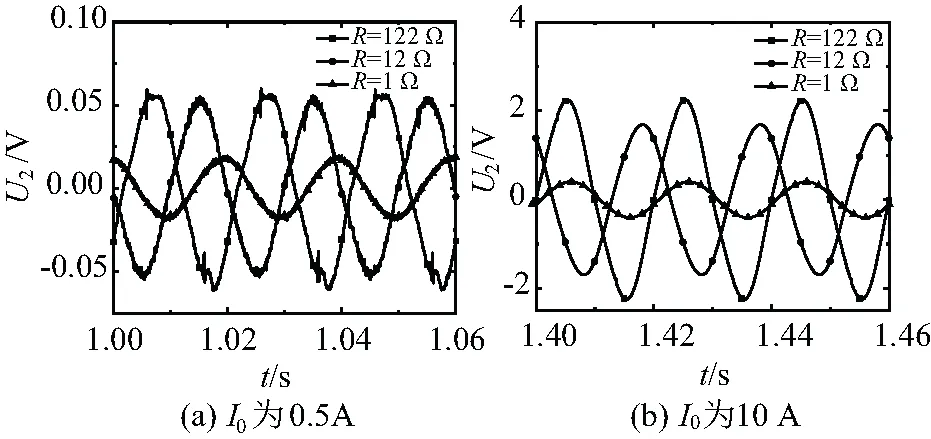
圖6 實驗過程中U2的波形
圖7為I0<20 A時,U2的均方根值與I0的關系的實驗結果。
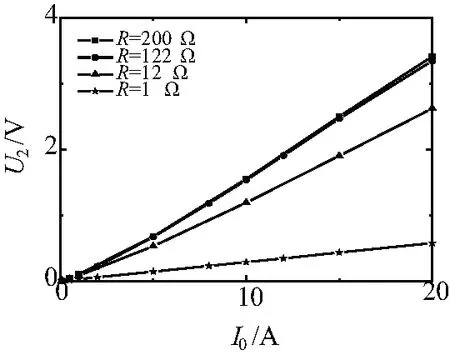
圖7 U2-I0實驗曲線
由圖7和圖4對比分析可知,仿真結果與實驗結果吻合。通過FFT對實驗數據進行處理,定量分析計算不同I0和R時,U2、實際功率S、εi以及δ的值,其中S=Is2(R+Z2),δ為負載電壓U2基波相位與I0相位之差。計算結果如表1所示。
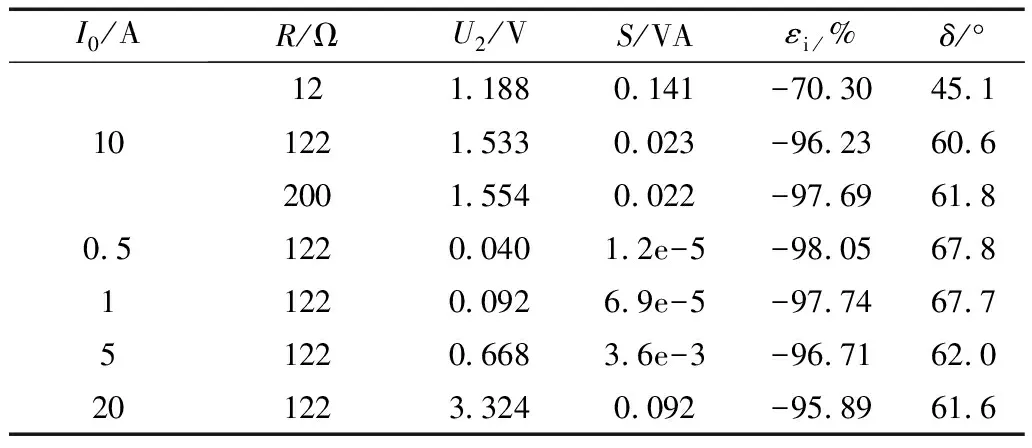
表1 零序TA實驗參數
通過表1可知,當I0不變時,隨著R增大,εi、δ和U2均增大,實際功率S減小。當R不變時,隨著I0增大,εi和δ均在一定范圍內變化,且其值遠大于額定誤差限值,但誤差的相對變化量較小,其中εimax-εimin=2.06%,δmax-δmin=7.2°。若在實際應用時需要提高比差和角差的精度,可通過查表的方式進行修正。對于文中的應用方式而言,上述比差和角差已經能夠滿足要求,因此不需要修正。
2 單相接地檢測
2.1 基本方法
由第1節可以看出,零序TA配大負載電阻時,盡管在一次電流較大時二次波形會有一些畸變,并且U2與I0成非線性關系,但是U2與I0仍是單調關系,因此仍可以根據二次側電壓U2反映一次側零序電流的大小,從而進行單相接地檢測。
由第1節還可以看出,當一次零序電流I0較小時U2與I0成近似線性關系,并且U2也比較大從而便于檢測,這就為零序電流較小的高阻接地的檢測提供了方便。
為了能夠有效地進行單相接地檢測,負載電阻R的參數很關鍵,在中性點不接地系統中可能遇到的最大零序電流時(一般小于20 A),其設計原則需同時滿足下列條件:
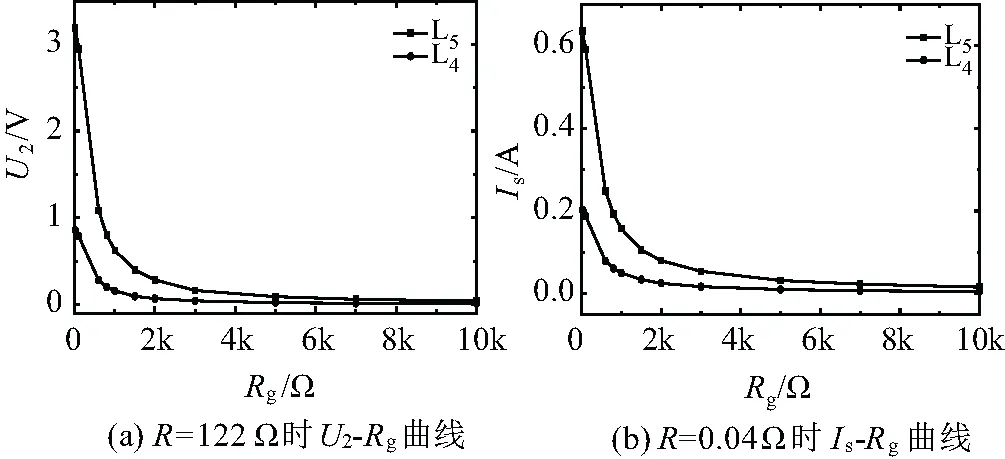
(1)U2 (2)流過R的功率PR 例如,對于1.3節例子中的150/5 A零序電流互感器的情形,R>100 Ω時均可滿足要求。 圖8(a)為一個基于零序TA配大電阻的用戶側分界開關單相接地保護裝置(WT)的構成,當U2大于閾值電壓UREF時,比較器輸出置位,驅動跳閘繼電器動作。圖8(b)為該裝置的布置示意圖。圖8中CB為變電站出線開關,F為線路分段開關。 圖8 單相接地保護裝置原理圖 由于用戶10 kV線路很短,一般不會超過0.5 km,而架空線每km電容電流小于0.03 A(電纜線路電容電流根據芯線截面不同,最大為1.8 A/km)[15],也即用戶線路自身電容電流不超過0.015 A(電纜線路為0.9 A),因此,可將該分界開關的一次側動作零序電流整定為1 A,超過這個值則反映一定是用戶內部發生了單相接地,對應的接地過渡電阻為5.5 kΩ。對于150/5 A的零序TA,一次側1 A對應的二次電流值僅為33.3 mA,但是配負載電阻大于100 Ω時,對應的U2大于90 mV,也即UREF可取為90 mV,且不需要配置二次TA。根據第1節的論述,隨著R的進一步增大,曲線的非線性程度也逐漸增大,且122 Ω以上時對斜率的增大程度逐漸減弱,因此推薦采用100 Ω~122 Ω。 圖9為一個基于零序TA配大電阻的單相接地選線裝置示意圖。零序TA采集各條出線零序電流信號,通過負載電阻R將U2信號輸送至選線裝置進行處理,判斷故障出線。 圖9 單相接地選線裝置原理圖 在MATLAB/Simulink中建立中性點不接地配電網仿真模型。仿真模型如圖10所示。 圖10 仿真模型 圖10中,變壓器為110 kV/10 kV,采用Y/Δ接線方式,額定容量為20 MVA。系統包含3條架空線路(L1、L3和L5),2條純電纜線路(L2和L4),單相接地故障發生在線路5(L5)8 km處。各線路參數如表2所示。 表2 仿真模型線路參數 文獻[16-18]在不同場景下經過反復實測接地電阻的結果顯示,接地電阻最小為18.84 Ω,最大為幾MΩ。在仿真時設置接地過渡電阻范圍為20 Ω~10 000 Ω。 圖11給出了各線路穩態零序電流(I0)與接地過渡電阻(Rg)的關系曲線。 圖11 各線路零序電流與接地過渡電阻的關系曲線仿真結果 由圖11可知,在Rg為20 Ω~10 000 Ω時,故障線路I0為0.488 A ~19.1 A。根據第1節的論述,隨著R的進一步增大,曲線的非線性程度也逐漸增大,且122 Ω以上時對斜率的增大程度逐漸減弱,因此推薦采用100 Ω~122 Ω。以R為122 Ω為例,對零序TA的單相接地檢測能力進行仿真驗證,并與R為0.04 Ω的情況進行對比。 圖12給出了Rg為20 Ω~10 000 Ω,R為122 Ω和0.04 Ω時,U2與Rg的關系曲線以及Is與Rg的關系曲線。 圖12 線路零序TA輸出信號對比曲線 由圖12(a)可知,當Rg為20 Ω~10 000 Ω時,在L5中零序TA二次電壓有效值U2-R122為0.039 V~3.185 V,兩條線路零序TA二次信號差值ΔU2=U2-L5-U2-L4為0.031 V~2.328 V。 由圖12(b)可知,當Rg為20 Ω~10 000 Ω時,在L5中零序TA二次電流有效值Is-R0.04為0.016 A~0.635 A,兩條線路零序TA二次信號差值ΔIs=Is-L5-Is-L4為0.011 A~0.432 A。 為了對比傳統零序電流檢測方法和文中論述的零序TA配大電阻檢測方法在單相接地選線時的效果,定義R=0.04 Ω時單相接地所在饋線與正常饋線零序TA二次側電流之差的相對值KI為: (10) 定義R=122 Ω時單相接地所在饋線與正常饋線零序TA二次側電壓之差的相對值KU2為: (11) 根據仿真結果,可以做出KI和KU2與Rg關系曲線,如圖13所示。 圖13 KI和KU2與Rg關系曲線 由圖13可見,在單相接地選線應用中,論述的檢測方法比傳統零序電流檢測方法的故障特征更明顯,對高阻接地的情形改進效果明顯。 對于中性點不接地配電網,零序電流互感器配適當的大負載電阻,可以直接利用其二次側電壓實現用戶側單相接地保護和變電站單相接地選線,而不需要配置二次電流互感器,使裝置構成更加簡單。 在單相接地選線應用中,零序電流互感器配適當的大負載電阻并檢測二次側電壓的方法比傳統零序電流檢測方法的故障特征更顯著,尤其是對于高阻接地的情形改進效果更為明顯。2.2 用戶側分界開關單相接地保護裝置
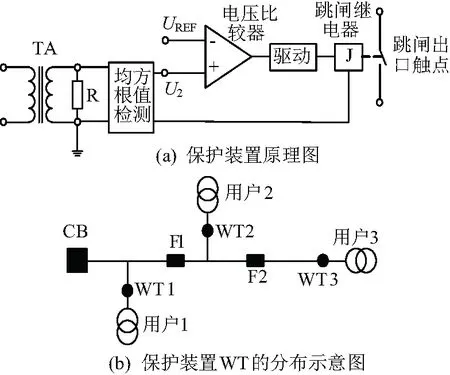
2.3 單相接地選線裝置
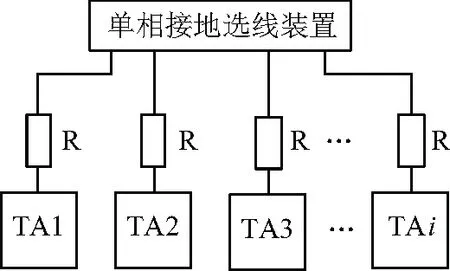
3 單相接地檢測性能仿真驗證

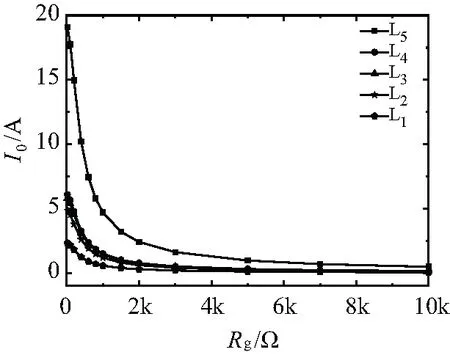
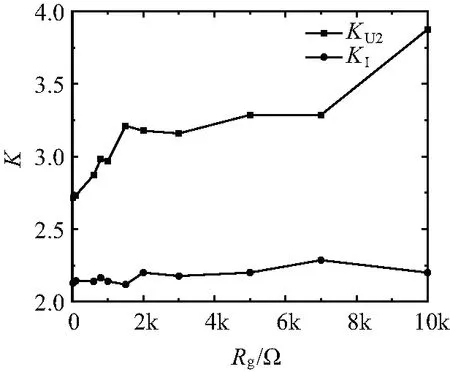
4 結束語

