晶向對鋁合金構件微動疲勞初始起裂的影響研究

王 建, 阮星源

(西南科技大學 土木工程與建筑學院, 四川 綿陽 621010)

微動疲勞是在材料疲勞和接觸部位微動磨損協同作用下,構件接觸界面附近發生的漸進損傷及開裂過程。微動疲勞現象廣泛存在于航空工業領域內各種機械構件中,加速結構構件接觸表面及淺表層裂紋的萌生與擴展,進而將造成發動機渦輪葉片榫頭斷裂、機身蒙皮脫落等事故,是復雜應力環境中長期服役的民用航空飛行器災難性事故的主要原因[1]。由于微動疲勞構件的相對位移幅度很小(微米級)、造成裂紋萌生及斷裂的循環次數很大(1萬次以上的高周疲勞)、裂紋發生的位置很隱秘,且裂紋發生后,難以采取有效措施抑制其繼續發展,因而微動疲勞又被視作難以處置的“工業癌癥”[2]。

超高強鋁合金AA7075作為一種航空鋁材,廣泛用于飛機的機身、機翼等各個部件中,并以鉚釘、螺栓、薄板等形式存在[3]。在航空飛行過程中,鋁合金板材和構件將面臨著微動疲勞導致的結構性能劣化和斷裂失事風險[4]。微動疲勞可分為初始起裂和裂紋擴展直至斷裂兩個階段;而初始起裂部位的辨識及裂紋萌生壽命的預測,在鋁合金微動疲勞研究中,具有重要的現實意義和迫切的實際需求。

微動疲勞影響因素可分為接觸狀態(接觸幾何形態、表面狀態及受力狀態等)、環境因素(溫度、濕度及環境介質等)和材料特性(材料成分、結構及宏細觀力學特性等)等三個方面[5]。在不改變接觸狀態和環境因素等條件下,材料特性作為微動疲勞的唯一可控因素,引起了國內外相關研究者的廣泛關注。研究者發現,可以通過不同的材料加工方法及表面處理技術改進接觸構件表層材料的性狀以提高其微動疲勞抗力[6],進而要求確立微動疲勞與材料細觀織構之間的關系,以更好地進行抗微動疲勞設計。而在材料加工與設計領域,對于材料細觀織構對構件微動疲勞性能的影響研究尚在探索中。Minaii 等[7]利用晶體塑性有限元研究了晶粒尺寸和規則參數等細觀結構特征參數對初始起裂壽命及起裂部位的影響。 McCarthy等[8]利用晶體塑性有限元研究了晶向對316LSS不銹鋼構件微動疲勞導致的磨損、塑性形變及應力狀態的影響。國內相關研究方面,包括田紅亮等[9],關海達等[10]和劉麗艷等[11]分別利用室內試驗、數值計算對結構部件微動部疲勞、磨損特性及機制所做的探索工作。當前,尚未見晶向對鋁合金構件微動疲勞影響的相關報道。

本文擬利用晶體塑性有限元模擬鋁合金試件在循環荷載作用下的微動疲勞過程,探討晶向對鋁合金晶體試樣初始起裂部位及裂紋萌生壽命的影響情況。文章主體內容分布于1～3章:第1章為微動疲勞模型設計;第2章為晶體塑性有限元模擬方法介紹及材料參數選擇,加載方式及荷載選擇,以及接觸模型驗證等;第3章為晶向對晶體試樣彈模及屈服強度的影響、晶向對初始起裂部位及裂紋萌生壽命的影響分析。

1 微動疲勞模型

服役期間交變荷載作用下飛機機身鉚釘-平板結構單個搭接接頭可簡化為圖1所示的微動疲勞計算模型,這也是常見的單夾具微動疲勞試驗的代表。平板接頭所受的橫向遠程振動荷載由同步、同相加載的軸向循環應力σA和軸向反作用應力σR分別施加于試樣兩側。

在微動墊模型上部邊界施加法向荷載P, 并采用多點約束(MPC),以模擬鉚釘的平穩擠壓作用。在微動疲勞工況下,微動墊-試樣接觸保持部分滑動狀態[12],即試樣頂部所受的切向作用力Q滿足條件Q滿足條件Q<μP,μ為摩擦因數,Q可表示為σA和σR的函數

(1)

式中,As為試樣的橫截面積。

為克服單元尺寸差異過大對數值計算所造成的困難,以實施微動疲勞宏-細觀耦合多尺度計算,我們采用了全局模型-子模型耦合的方法計算交變荷載作用下試樣晶粒內部的彈塑性響應。計算模型尺寸依據Vazquez 等[13]室內微動疲勞試驗模型尺寸取值。全局模型中試樣長度和寬度分別為 30 mm 和 5 mm。 微動墊接觸面圓弧部分半徑為 100 mm。除了圓弧部分外,微動墊模型的寬度和高度都被截斷為 20 mm,以滿足圣維南原理中關于邊界效應的消除原則。選擇三節點線性平面應變三角形單元 CPE3對微動墊和試樣進行網格劃分。為了解決試樣尺寸、接觸半寬尺寸的受限問題,我們在晶體塑性有限元微動疲勞模擬中對試樣采用了子模型-全局模型耦合技術,如圖1所示。子模型與微動墊毗鄰,其尺寸為10 mm × 2.5 mm。子模型由NEPER軟件[14]隨機生成741顆直徑為150 μm的晶粒。晶粒同樣由CPE3單元剖分,單元長度設為50 μm,其單元總數為9 968個。以每一時步全局模型-子模型界面處全局模型位移計算結果Ux和Uy作為子模型左右側和底部動力邊界條件;子模型與上方微動墊的接觸特性及加載方式均與全局模型一致。在子模型所在區域范圍內,試樣全局模型單元長度為0.1 mm;在子模型所在區域范圍外,試樣全局模型單元長度逐漸由0.1 mm增加到左、右邊界處的0.2 mm。微動墊模型單元長度由接觸面上的0.05 mm逐漸過渡到頂面的0.5 mm。試樣模型和微動墊模型分別劃分了23 800個和39 682個CPE3單元。微動墊和試樣這兩個組件的材料均為Al 7075-T651 合金。對于彈性接觸而言,試樣和微動墊的力學參數均設置為楊氏模量E= 71 GPa 和泊松比ν= 0.33。就接觸設置而言,微動墊的圓弧表面定義為接觸副的主表面,而試樣上表面定義為從表面。 采用拉格朗日乘子摩擦公式描述接觸區域的切向行為,根據試驗測試結果,其摩擦因數μ=0.72。 此外,對于幾何特性而言,平面外表面厚度設置為 7 mm。

2 晶體塑性有限元方法

2.1 晶體塑性公式

晶體塑性有限元法可以模擬循環荷載作用下晶粒內部滑移帶錯動所引發的微觀塑性變形,因而可用于模擬微動疲勞現象。本文選用了Marin 等[15]開發的解釋彈性和塑性變形的晶體彈黏塑性本構模型,并利用 Armstrong-Frederick 運動硬化規則對其進行了修改,以適應循環背應力(backstress)的作用。該本構模型假設晶體滑移是塑性變形的唯一機制,而忽略其他機制,例如孿晶、晶界滑動和擴散。 單晶的彈塑性變形梯度F可以乘法分解為彈性分量Fe和塑性分量Fp,彈性變形梯度Fe也可以分解為對稱彈性拉伸張量Ve和正交旋轉張量Re,即彈塑性變形梯度F可以表示為如下形式

F=FeFp=VeReFp

(2)

塑性速度梯度Lp定義為所有滑移系上的剪應變速率之和[16],即

(3)

第α個滑移系上的剪切應變率用式(4)所示的經驗冪律方程流動法則[17-18]計算

(4)

(5)

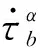
2.2 材料特性和晶向參數校正

為了與微動疲勞模型一致,本文擬采用二維代表性體積單元(2D RVE)進行參數識別和校正。2D RVE具有兩個基本假設:平面應變條件和二維尺度。Vuppala 等[20]通過研究發現,平面應變假設對織構演變幾乎沒有影響。此外,2D模型的部分缺陷可通過增加晶粒數量克服[21];并且2D模型計算結果也可映射到3D模型[22]。

本文所選用的AA7075晶體本構關系所需參數源于先前工作基礎[23]。晶體織構直接基于電子背散射試驗(electron back scatter diffraction, EBSD)試驗結果,而結晶本構方程的參數通過反分析識別。 彈性材料 C11、C12 和 C44 采用 Hosford試驗結果[24]。主要參數如表1 所示。

表1 AA7075材料晶體本構模型參數Tab.1 Calibrated parameters of the crystalline constitutive law for AA7075

除了晶粒形態外,晶體各向異性的其他主要來源是織構或晶向。晶粒初始織構通過電子背散射衍射(EBSD)測試獲得,并導入到晶體塑性有限元模型中。如圖2所示,本文選取了AA7075材料試驗擬合晶向(簡稱試驗晶向),隨機分布晶向(簡稱隨機晶向)和隨機偏轉±10°的(111)晶向(簡稱(111)晶向)進行對比分析。其中,試驗擬合晶向是對Li等[25]電子背散射測試(EBSD)結果的擬合。

(a) 電子背散射測試結果

(b) 試驗擬合晶向

(c) 隨機晶向

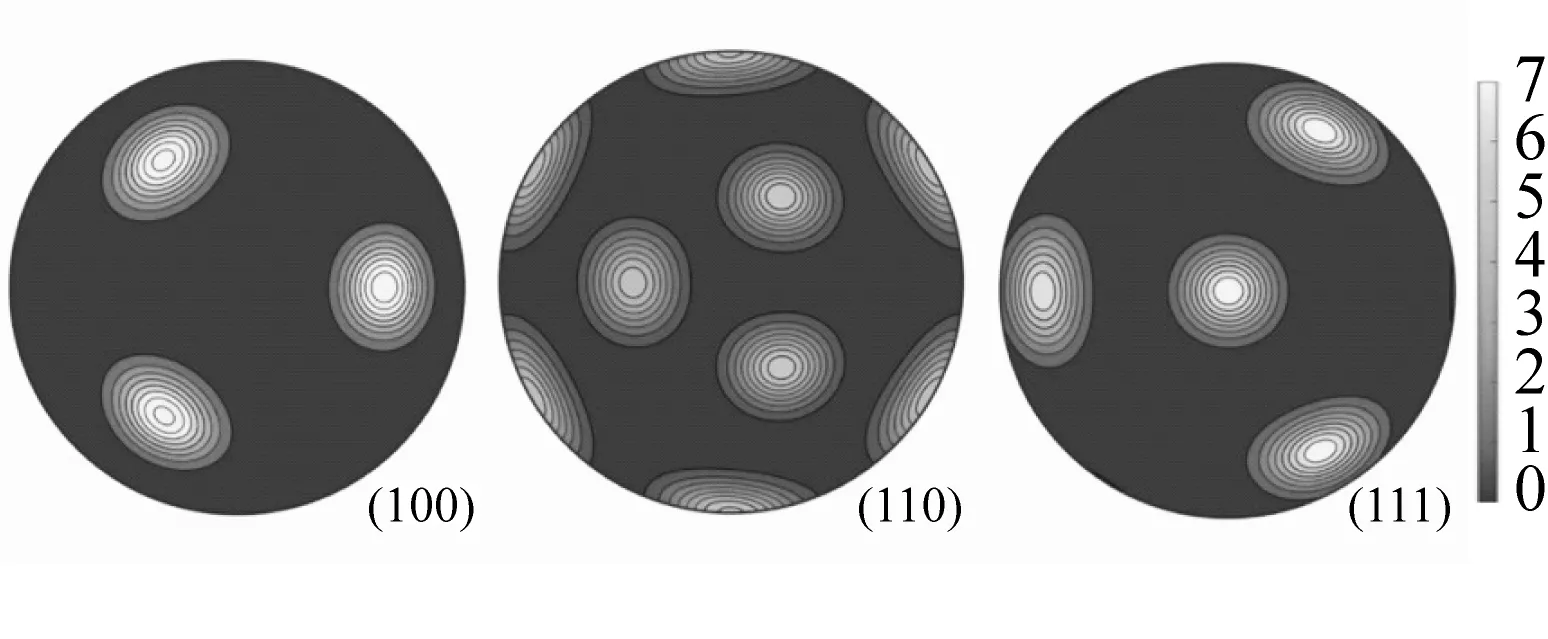
(d) (111)晶向圖2 AA7075晶體織構赤平極射投影圖Fig.2 Pole figures of AA7075

2.3 模型驗證

根據Hertz彈性接觸理論[26],微動墊-試樣接觸面的歸一化接觸應力如式(6)所示

(6)

式中:p0為接觸表面的最大應力;a為接觸半寬。

本文所用的二維模型微動墊-試樣相互接觸與圓柱體與半平面之間的接觸等效。根據Nowell等[27]的研究成果,圓柱體與半平面接觸面上的歸一化剪切牽引力如式(7)所示

(7)

式中:c為黏著區的接觸半寬。c由式(8)所示

(8)

e為黏著區中心與接觸中心之間的偏移量,可由式(9)所示

(9)

圖3為微動墊-試樣模型接觸界面處歸一化接觸壓力和歸一化剪切牽引力的解析解和 FEM 解之間的比較。Nowell等[27]研究發現,當試樣的半寬大于或等于接觸半寬的10倍時,則數值模型滿足Hertz解的假設條件;當試樣半寬與接觸半寬之比等于3時[28],數值計算結果與解析解之間的偏差高達20%。盡管本文試樣模型的寬度不滿足完全彈性半無限空間假設,但歸一化接觸壓力和歸一化剪切牽引力的解析解和數值解之間吻合得很好,表明本文所采用的模型獲得了很好的驗證。

(a) 歸一化接觸壓力

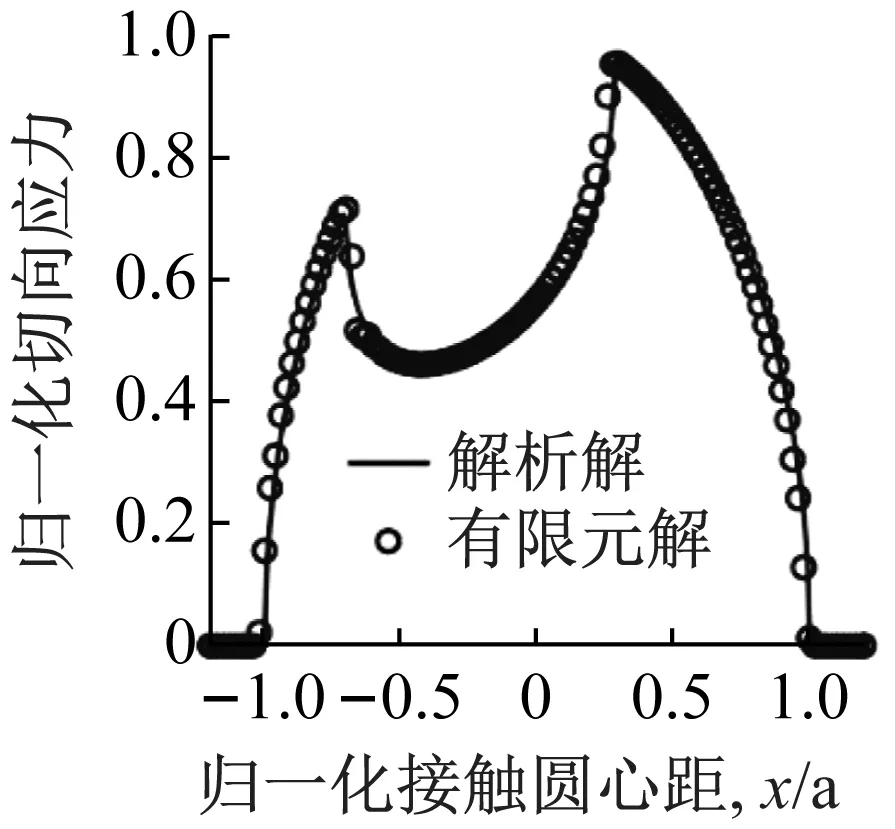
(b) 歸一化剪切牽引力圖3 解析解與有限元數值解的比較Fig.3 Comparison of analytical and FEM solutions

2.4 加載方式

根據時序關系,微動疲勞模擬過程可分為兩個不同的階段:初始加載階段和微動循環加載階段,如圖4所示。在初始加載階段(即圖4中的時步0),逐漸將法向荷載P施加到設定值,使微動墊和試樣之間建立穩定的接觸關系,隨后在保持P值恒定。在微動循環加載階段,在試樣端部同步施加相位差為0的軸向體積應力σA和軸向反作用應力σR。循環荷載加載過程中,軸向應力比(最小軸向應力與最大軸向應力之比)和切向載荷比(最小Q與最大Q之比)均等于-1。為了將這些加載預設值準確發送到 Abaqus求解器,每個循環劃分為四個階段:加載階段(如時步1)、卸載階段(如時步2)、反向加載階段(如時步3)和反向卸載階段(如時步4)。為與微動疲勞試驗一致,循環加載頻率設置為 10 Hz。

圖4 軸向應力σA和軸向反力σR相位差為0時的一個完整循環的加載次序Fig.4 Loading sequence of one complete cycle for 0° phase difference between σA and σR

在本文的計算中,我們模擬了300個循環次數的微動疲勞作用,加載參數設定值如表2所示。

表2 微動疲勞模擬加載工況Tab.2 Loading conditions selected for fretting fatigue simulation

3 晶體塑性有限元方法

3.1 晶向對晶體彈模及屈服強度的影響

不同晶向試樣單軸拉伸應力應變模擬曲線如圖5所示。其中,試驗晶向試樣,隨機晶向試樣和(111)晶向試樣的赤平極射投影圖分別見圖2(b)～(d)。單軸拉伸試樣采用圖1中的子模型尺寸,單軸拉伸速率與微動疲勞模擬中循環荷載軸向加載速率相同,即應變率均為0.001 s-1。

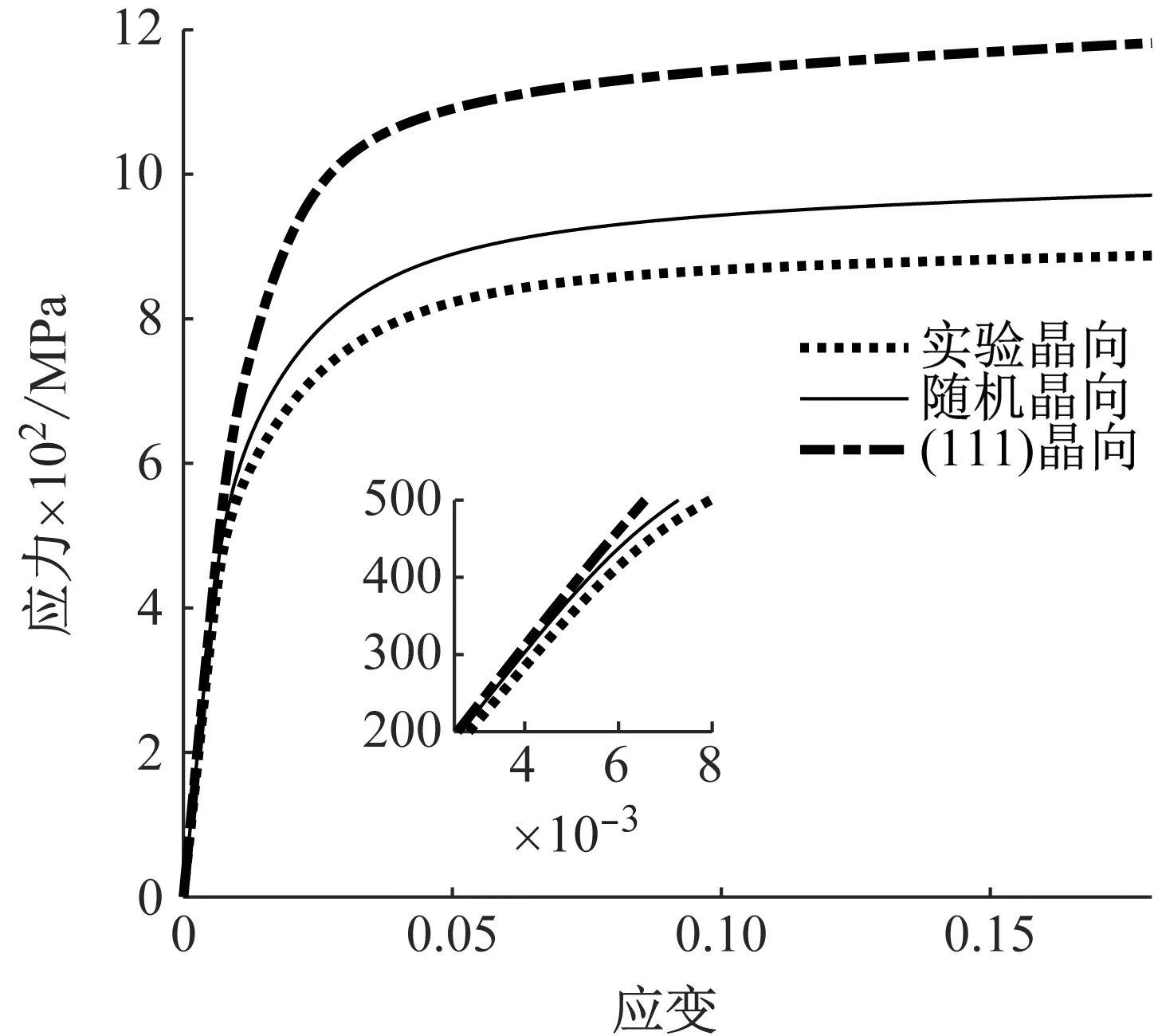
圖5 單軸拉伸條件下晶體試樣應力應變曲線Fig.5 Stress-strain simulation curves of specimens with different crystallographic orientations under uniaxial tension

在彈性域內,試驗晶向單軸拉伸模擬所得的彈性模量為69.4 GPa, 與Boller等[29]的試驗結果71 GPa相差僅約2%; (111)晶向試樣的彈性模量最大,為77.5 GPa; 隨機晶向試樣的彈性模量居中,為76.4 GPa。此外,試驗晶向試樣屈服強度和硬化強度均最小; (111) 晶向試樣的屈服強度大于隨機晶向試樣,而其硬化強度低于隨機晶向試樣。由此可見,(111) 晶向試樣的宏觀彈模及屈服強度最大,隨機晶向試樣次之,而試驗晶向試樣最小。

3.2 晶向對微動疲勞初始起裂部位的影響

300次微動疲勞循環加載后,試驗晶向, 隨機晶向和 (111) 晶向這三種晶向試樣等效塑性應變云圖,如圖6所示。三種晶向的接觸面初始起裂部位均發生于接觸后緣附近的E1714單元或與E1714單元相鄰的E5993單元內部。由此可見,晶向分布對接觸面初始起裂部位影響不大。

(a) 試驗晶向

(b) 隨機晶向

(c) (111)晶向圖6 300次循環加載后微動疲勞等效塑性應變極值點位置Fig.6 The location of fretting fatigue PEEQ extreme point after 300 cyclic loadings

三種晶向試樣內部均存在多個等效塑性應變(equivalent plastic strain, PEEQ)極值所對應的初始起裂熱點。PEEQ越大的單元,其所在的部位越可能開裂。因此,可以通過不同晶向試樣的等效塑性應變分布云圖預判微動疲勞初始起裂點位置[30]。不同晶向試樣內部微動疲勞初始起裂點位置識別如下:試驗晶向試樣的初始起裂點位于微動墊-試樣接觸中線附近,接觸面以下1.28 mm的E2608單元處;隨機晶向試樣的初始起裂點位于接觸面以下1.41 mm的E1495單元處;(111) 晶向試樣的初始起裂點位于接觸面以下1.56 mm的E1837單元處。結合不同晶向試樣的宏觀屈服強度可知,試樣彈模及屈服強度越大,其初始起裂部位越深。就PEEQ分布形態而言,三種晶向試樣均表現出不同程度的各向異性。試驗晶向試樣PEEQ云圖呈傾斜條帶狀分布,(111) 晶向試樣PEEQ云圖呈絮狀分布,而隨機晶向試樣PEEQ云圖介于條帶狀與絮狀分布之間。可以預見,PEEQ分布形態將影響到裂縫發軔及擴展特征。由此可見,不同晶向試樣,其亞表面裂縫發軔位置及擴展特征均有所不同。

3.3 晶向對塑性應變能密度及微動疲勞裂紋萌生壽命的影響

晶系滑移過程中所耗散的能量可用塑性應變能密度(PSED)?衡量[31],其單次循環作用過程中所有滑移系所耗散的能量可由式(10)所計算

?=∮cσ:dεp=∑∮ταdγα

(10)

式中:σ為有效應力,εp為晶系滑移產生的累積塑性應變;τα和γα分別為作用于滑移系α的剪應力和塑性剪應變。根據以往計算發現,單個循環的塑性應變能密度與其累積值成正比關系;且在循環加載過程中,單次循環作用所耗散的塑性應變能會隨著加載的進展發生細微的變化,因此,本文僅考慮累積塑性應變能密度時程曲線的分布特征。

此外,初始起裂壽命N與?之間的關系可由式(11)表示

(12)

式中,f(x)為能量吸收系數、最小工程可檢裂紋長度、平均位錯間距,以及彈性模量、泊松比等參數的函數。由此可見,塑性應變能密度與初始起裂壽命成反比關系。

不同晶向試樣接觸面和試樣內部初始起裂點的總累積塑性應變能密度時程曲線(plastic strain energy density, PSED),如圖7所示。對于接觸面初始起裂部位和模型內部初始起裂部位而言,試驗晶向試樣的PSED曲線斜率及所對應的單次循環塑性應變能密度最大,(111)晶向試樣的PSED曲線斜率及所對應的單次循環塑性應變能密度最小,因此,試驗晶向試樣的初始起裂壽命最小,(111) 晶向試樣的初始起裂壽命最大,隨機晶向試樣的初始起裂壽命居中。此外,對于同一種晶向試樣,其接觸面初始起裂部位PSED均小于模型內部初始起裂點PSED,表明在當前采用的荷載和接觸條件下,模型內部更易于起裂。綜上所述,晶體試樣彈模和屈服強度越大,其微動疲勞初始起裂壽命越大,即試樣初始起裂壽命與材料強度成正相關關系。

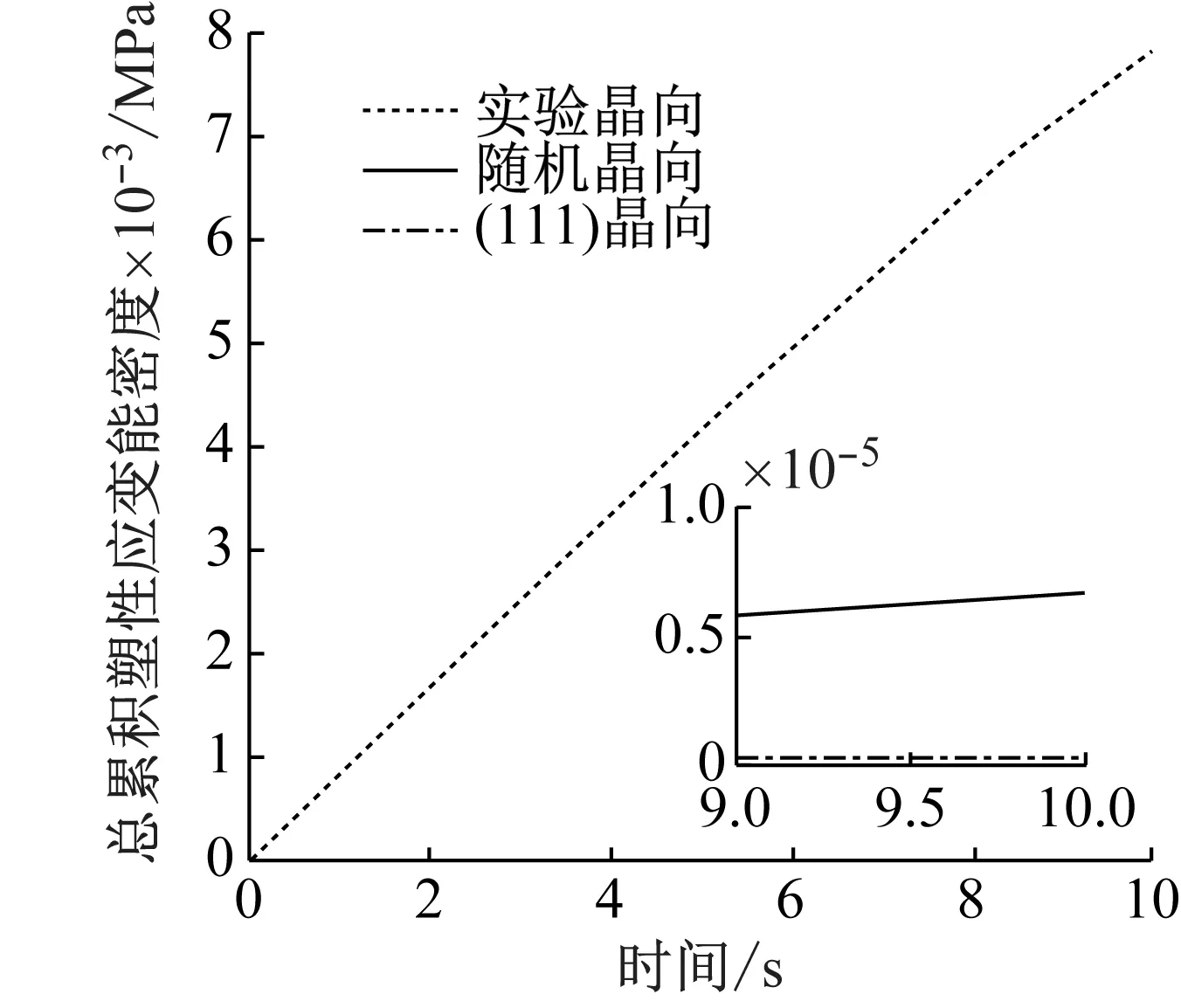
(a) 接觸面初始起裂點

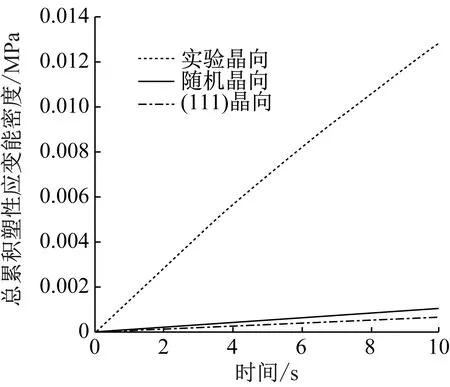
(b) 內部初期起裂點圖7 晶向試樣累積塑性應變能密度時程曲線Fig.7 Time history of accumulated plastic strain energy density

4 結 論

(1) 晶向分布將對晶體材料的彈性模量和屈服及硬化強度造成明顯影響。(111)晶向試樣的彈性模量最大和強度最大,隨機晶向試樣的彈性模量和強度居中,而一般試驗晶向試樣的彈性模量和強度均最小。

(2) 晶向分布對微動疲勞接觸面起裂部位的影響不明顯,而對亞表面起裂部位影響比較顯著。(111)晶向試樣的亞表面初始起裂點最深,隨機晶向試樣次之,而一般試驗晶向試樣的亞表面初始起裂部位最淺。

(3) 晶向分布對微動疲勞初始起裂壽命的影響比較明顯。(111) 晶向試樣的初始起裂壽命最大,隨機晶向試樣的初始起裂壽命居中,而試驗晶向試樣的初始起裂壽命最小。

上述結論表明,晶向分布這一細觀織構影響了晶體材料宏觀尺度的彈性強度特征和塑性變形特征,并對金屬構件微動疲勞初始起裂壽命、亞表面裂縫發軔位置及擴展特征均造成了影響。利用材料加工方法改變金屬晶體試樣淺表層的晶向分布狀態,將可以抑制微動疲勞裂縫的發軔及擴展。