引入動態分化和鄰域誘導機制的雙蟻群優化算法

禹博文　游曉明　劉升

摘 要：為提高傳統蟻群算法在解決旅行商問題時的優化效果，提出了一種引入動態分化和鄰域誘導機制的雙蟻群優化算法。該算法首先引入混沌隨機策略，在算法初始化階段改變原始的貪心策略，使初始信息素混沌分布，以保持種群的多樣性，從而提高解的精度；其次，將蟻群分為孤立蟻群與正常蟻群，兩組螞蟻分別在當前最優路徑與離群路徑附近搜索；在種群間采取誘導機制，正常蟻負責搜索最優路徑，孤立蟻混沌隨機釋放信息素，將正常蟻群誘導至新的路徑鄰域，從而有效地平衡收斂速度與解的多樣性之間的矛盾。通過對不同規模的旅行商問題仿真結果的比較，驗證了所提算法的有效性。

關鍵詞：旅行商問題； 蟻群優化； 動態分化策略； 混沌隨機； 誘導策略

中圖分類號：TP18 文獻標志碼：A 文章編號：1001-3695（2023）10-018-3000-07

doi：10.19734/j.issn.1001-3695.2023.02.0060

Dual-ant colony optimization algorithm with dynamic differentiation and neighborhood induction mechanism

Yu Bowena， You Xiaominga， Liu Shengb

（a.School of Electronic & Electrical Engineering， b.School of Management， Shanghai University of Engineering Science， Shanghai 201620， China）

Abstract：In order to improve the optimization effect of traditional ant colony algorithm in solving traveling salesman problem， this paper developed a dual-ant colony optimization algorithm with dynamic differentiation and neighborhood induction mechanism. Firstly， the algorithm introduced chaotic random strategy， and changed the original greedy strategy in the initialization stage of the algorithm to chaotic distribute the initial pheromone， so as to maintain the diversity of the population and improve the accuracy of the solution. Secondly， the algorithm divided the isolated ants in the ant colony into isolated ant colony and normal ant colony， and the two groups of ants searched around the current optimal path and the outlier path respectively. It adopted the induction mechanism among the populations. Normal ants were responsible for searching the optimal path， and isolated ants released pheromones randomly in chaos to induce the normal ant colony to a new path， thus effectively balancing the contradiction between the convergence rate and the diversity of solutions. The simulation results of different scale TSP show the effectiveness of the proposed algorithm.

Key words：traveling salesman problem; ant colony optimization; dynamic differentiation strategy; chaos random; induction strategy

0 引言

旅行商問題是一種組合優化問題，其目的是給定一組城市的坐標，求出遍歷所有坐標并返回起始位置的一條最短路徑。旅行商問題是一種NP難問題，在運籌學與計算機科學中具有非常重要的地位。目前有許多算法被提出用于解決TSP問題，如模擬退火（simulated annealing，SA）、遺傳算法（genetic algorithm，GA）、螞蟻算法（ant system，AS）［1］等。其中螞蟻算法在TSP上有較好的效果。

螞蟻算法是意大利學者Dorigo提出的一種啟發式全局搜索算法，通過模仿自然界中螞蟻釋放信息素尋路的過程實現路徑搜索。蟻群算法具有分部性、隨機性、動態性等優良性能，并且具有很好的可移植性［2］，能被應用在不同種類的問題上。目前被廣泛應用于車間調度［3］、路徑規劃［4］、路由問題［5］和求解旅行商問題［6］上。傳統螞蟻算法存在一定的局限性。例如蟻群算法在搜索初期缺乏信息素，延遲了算法的收斂速度。在算法的中后期，由于信息素大量積累在部分路徑，導致固定路徑的選擇概率過高，容易使算法陷入局部最優，影響解的質量。于是Dorigo等人[7]在螞蟻算法的基礎上提出了蟻群算法（ant colony system，ACS）提出了全局信息素更新，加快了求解TSP時的速度。Stutzle等人［8］在2000年又提出最大—最小蟻群算法（max-min ant system，MMAS），設置了每條路徑上的信息素上下限，提高了解的質量。

針對算法收斂速度慢的問題，許多學者在蟻群算法的基礎上作出了改進。文獻［9］引入了信息熵理論，通過計算信息熵判斷蟻群的離散度，根據系統的離散程度調整算法參數提高解的性能。但是在前期信息熵濃度較低時，不能很好拓展解的多樣性容易導致在前期陷入局部最優。文獻［10］利用貪心算法求解蟻群算法的初始解，然后計算初始解的次優解，對次優解也給予一定的信息素獎勵，加快了解的收斂速度。同時在算法后期引入變異操作，選取當前最優路徑附近的路徑進行加權。然而，根據貪心算法計算得出的最優解與次優解有可能與真實最優解距離較遠，有可能在算法的初期陷入局部最優。在算法容易陷入局部最優解的問題上也有許多改進算法被提出，文獻［11］融合狼群算法的分級策略，依據解的大小將蟻群分為不同等級的螞蟻，并根據不同螞蟻的地位分配不同的權重，使精英螞蟻能夠分泌更多的信息素，對蟻群起指導作用。文獻［12］在結合精英蟻群機制的基礎上加入了頭狼算法，即對每一個螞蟻加入搜索半徑，精英蟻選擇搜索半徑內的任意一個節點進行跳變。同時在陷入局部最優后對局部最優節點的信息素進行稀釋，達到跳出局部最優的目的。但精英策略在搜索時搜索速度較慢，經常導致算法的運行時間過長。文獻［13］在精英策略的基礎上增加了自適應分組策略，各個組螞蟻的數目能夠動態調整并在組間增加了學習策略，但自適應分組只是將螞蟻分為數量不同的組，并沒有對每組螞蟻進行分工。文獻［14］將3opt搜索算法與改進蟻群算法相結合，利用3opt算法的近鄰搜索能力拓展搜索空間，在保證搜索速度的同時提高了算法的局部搜索能力。文獻［15］提出一種刺激響應機制，根據不同任務設置響應閾值，按照不同任務刺激的大小對螞蟻進行分工，當任務刺激超過某只螞蟻的響應閾值后將該螞蟻分配至對應任務，同時引入正負反饋調節機制，根據種群多樣性利用正負反饋調節螞蟻數量，平衡了收斂速度與全局搜索能力，但以上幾種算法面對大規模TSP時往往效果不好，收斂速度慢，且容易陷入局部最優解。

針對上述蟻群算法搜索速度慢，在大規模問題上解的精度不高等問題，本文通過加入以下策略提出一種引入動態分化和鄰域誘導機制的雙蟻群優化算法（ICACO）。在搜索的前期引入混沌隨機策略［16］，使地圖中的信息素和螞蟻的位置進行混沌隨機更新，取代傳統蟻群算法初始化時的貪心策略［10］，在搜索前期使信息素隨機地散布在各條路徑上以增加解的多樣性；其次，提出一種孤立分化機制，首先，根據信息素、路徑長度構建歸一化模型，按照信息素的分離度使蟻群分為正常種群和分化種群，正常種群沿當前信息素最大的路徑探索，孤立種群沿新路徑進行搜索，并在新路徑上混沌更新信息素值，一旦發現更優路徑即釋放更多的信息素于更優路徑上并將正常種群引導至新的路徑。實驗結果表明，本文算法相比于原始算法提高了收斂速度和解的質量，在大規模TSP上表現更好。

1 相關工作

1.1 蟻群算法（ACS）

蟻群算法是一種模擬自然界蟻群覓食行為的啟發式算法。螞蟻在覓食過程中會留下信息素，其他螞蟻在前進時會更大概率選擇信息素濃度較高的路徑。相同時間內在較短路徑上積累的信息素變多，蟻群便找到最短路徑，在旅行商問題上有很好的表現。蟻群算法相對于最初的螞蟻算法（AS）增加了信息素的局部揮發。即每只螞蟻走過一段路徑后，其留下的信息素就會立即揮發一部分，而非全體螞蟻走過后信息素的全局揮發。其更新規則為

其中：τ（i，j）為節點i到j之間的信息素；ρ是信息素的局部揮發率；Δτ（i，j）為節點i與j之間的信息素增量；釋放信息素后，螞蟻按照式（2）選擇下一個節點。

其中：pkij表示螞蟻k從節點i到j的概率；τij（t）表示節點i到j之間t時刻的信息素總量；η表示節點i到j之間距離的倒數;β為權重因子，代表啟發信息對路徑選擇的影響程度，β越大則啟發信息對路徑選擇的影響程度越大；allowedk表示螞蟻k還未走過的節點。所有螞蟻遍歷過一次后進行信息素的全局更新，對所有路徑上的信息素進行更新，更新方式如式（5）所示。

其中：α為全局信息素揮發系數，代表上一次迭代后信息素的殘留比例；Q為信息素更新權重;dbest為全局最短路徑；ACS在全局信息素更新時只留下全局最優螞蟻的信息素。并且隨著迭代次數的增加，最優路徑上的信息素不斷累加，會導致算法陷入局部最優。

1.2 動態分級的改良螞蟻算法

為了解決傳統蟻群算法收斂速度慢的問題，文獻［9］提出一種動態分級的螞蟻算法，按照分級因子將螞蟻分為四個等級，根據等級的高低為螞蟻劃分不同的信息素更新權重，等級高的螞蟻可以釋放更多的信息素，同時又給予等級低的螞蟻一定的信息素釋放量以增加算法的多樣性。定義分級因子為

其中：di為螞蟻遍歷所有節點走過的路徑長度;dmin為當前最短路徑。各個等級的螞蟻數量隨迭代次數調整，其信息素更新方式與式（5）相同，不同之處在于信息素增量Δτ（i，j），定義為

其中：Q1、Q2、Q3為各個等級能釋放的信息素總量，處于第一等級的螞蟻釋放信息素最多，依次遞減，處于最后一級的螞蟻禁止釋放信息素；n1、n2、n3為各個等級螞蟻的數量。通過各個等級螞蟻數量的不斷調整最終達到算法的平衡。

1.3 Logistic混沌隨機

混沌隨機是一種利用混沌映射產生隨機數的策略，具有非周期、不收斂的特性，其中應用較為廣泛的為Logistic映射，其表達式為

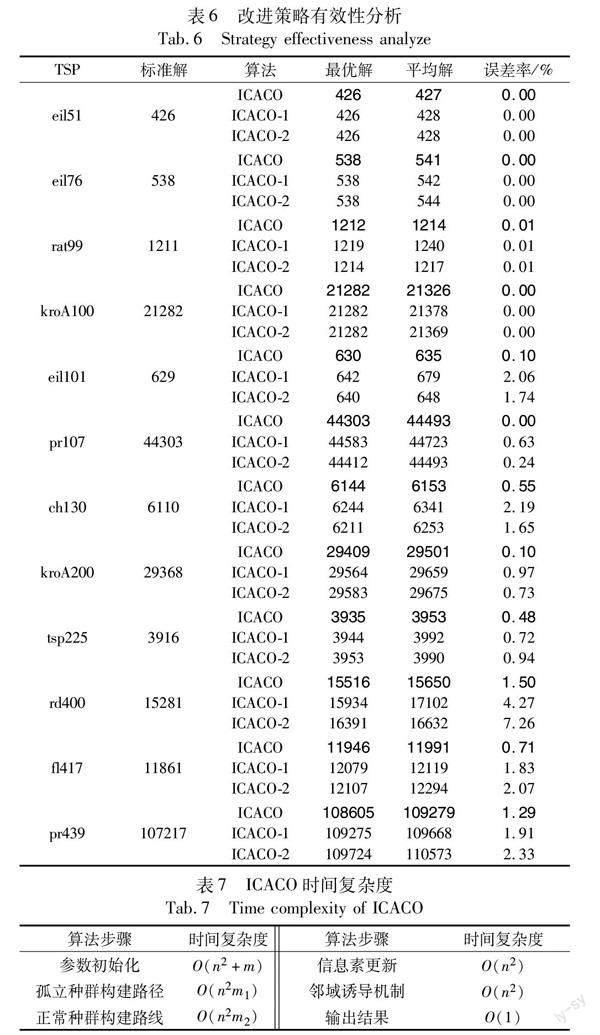
其中：xn+1、xn為混沌序列值;k為混沌因子。混沌序列的作用在于產生一列非線性、不可預測的隨機數，這些數字在k取3.569

2 引入動態分化和鄰域誘導機制的雙蟻群優化算法

2.1 算法的混沌初始化

在蟻群算法的初期，地圖上沒有信息素，導致算法前期搜索速度慢，同時由于只能利用距離信息初始化算法，導致算法前期易陷入局部最優［8］。并且由于傳統產生隨機數的策略為偽隨機策略，在大規模TSP時不利于種群的搜索多樣性。所以在蟻群搜索的前期，在各個城市路徑上混沌更新信息素量，使系統前期各個路徑上散布隨機量的信息素，避免蟻群盲目搜索，增加系統的收斂速度。同時，由于混沌更新的不可預測性與隨機性，避免了傳統蟻群算法根據貪心算法初始化導致的部分路徑完全不會被搜索到，增加了系統解的多樣性避免前期陷入局部最優。算法具體更新方式如下：

其中：i為當前迭代次數；當算法第一次迭代時，各個城市間的距離信息作為初始化信息素τ0加上混沌序列產生的隨機信息素信息，其中q為混沌調節因子，用于調節系統初始化時的混沌程度，q越大則系統信息素初始化時會更隨機。式中c為Logistic混沌參數，c的值越大則混沌程度越大，產生出的隨機數更隨機，n為總城市數，b為控制因子；當迭代次數小于n/b定義為初始化階段，在初始化階段系統信息素更新采用混沌更新方式，保證信息素廣泛散播。

2.2 孤立分化策略

2.2.1 孤立策略

傳統蟻群搜索的過程存在一定的盲目性，每只螞蟻都只在信息素濃度最高的路徑上搜索，這導致算法只聚焦于搜索最優解而忽視了其他路徑，其他路徑有可能蘊涵著真正的最優解。在大規模TSP問題中該問題尤其突出。在所有螞蟻遍歷完各城市后，會得到此次遍歷路線的總長度，每一只螞蟻得到的路線和總長度不同。在算法后期，大多數螞蟻會選擇相同的路線，部分螞蟻會選擇新的路線，即使新路線的路徑長度大于次優路線長度，這些新路線中可能包含全局最優路徑的一部分，本節利用孤立種群策略挑選出走新路線的種群形成孤立種群，然后將信息素與其他個體不同的路線片段提取并加強該路徑上的信息素，提高算法的路徑選擇能力。

孤立種群判定：

在系統經過一定次數迭代后，將對原始種群進行動態分化，迭代次數如式（11）所示。

其中：T1為左閾值，T2為右閾值；Lx是第x只螞蟻走過的路徑長度，Ly是第y只螞蟻走過的路徑長度；m為螞蟻總數。將所有螞蟻走過的路徑按路徑長短從小到大排列，走過路徑超過左右閾值的個體被認定為孤立個體。

2.2.2 分化策略

當孤立種群確定后，螞蟻將分為正常種群和孤立種群，正常種群仍然按照原始路徑搜索，孤立種群按照式（16）進行信息素更新，孤立種群在新路徑的周圍搜索，擴大了解的范圍。當發現比當前最優路徑更短的路徑時，蟻群將釋放更多的信息素在更優路徑上。孤立種群在最優路徑的周圍利用Logistic混沌釋放隨機量的信息素，直到更優路徑的產生，并將蟻群引導到新的位置。孤立種群信息素更新方式為

誘導機制：

在對原始蟻群進行分化后，孤立種群將按照式（16）釋放信息素。為了更好地擴大搜索空間，本文提出一種誘導機制，當孤立種群找到更優路徑后，將原始路徑上的信息素清空，加強孤立種群所釋放出的信息素濃度并將其擴散，將原始種群引導至孤立種群所發現的新路徑周圍，施行誘導機制后信息素分布如圖4所示。在種群分化后，首先將孤立種群所走過的路線進行one-hot編碼［17］，然后與原始路徑上的信息素相乘，使信息素矩陣只保留孤立種群所留下的信息素，如圖5所示。誘導公式如式（17）所示。

其中：τ為所有路線上的信息素;Li為按照one-hot編碼后孤立種群走過的路徑矩陣，即將每一步中孤立種群選擇的路徑置1，未選擇的路徑置0，使孤立種群釋放的信息素擴散至鄰域，將蟻群引入新的路徑。

2.3 算法流程

a）初始化算法各參數：最大迭代次數imax、各個種群螞蟻數量m，與α、β、ρ、c等參數，讀入城市位置數據。

b）利用混沌序列產生隨機數量的信息素分配到各條路徑，再利用混沌序列產生每只螞蟻起始位置。

c）每只螞蟻按照位置更新公式進行搜索，找到一條完整路徑。記錄當前迭代最短路徑長度。

d）計算路徑不變代數是否超過閾值G，若超過則啟動孤立分化，選擇出孤立種群。

e）分化后的孤立種群按照新的信息素更新方式釋放信息素。

f）孤立種群找到更優路徑時按照誘導機制將原始種群誘導至新的路徑搜索。

g）判斷是否達到結束條件，若未達到則返回步驟b）否則結束算法并記錄結果。

算法流程如圖6所示。

3 實驗結果

為了驗證和分析本文算法的有效性，選取TSPLIB中幾個典型問題進行仿真測試與傳統蟻群算法ACS、ACS+3opt進行比較，并與其他同類算法進行比較。在小規模和大規模問題上分別選取不同的算法進行對比，以驗證算法在面對大規模問題時的有效性。同時針對算法的收斂速度，將算法與基本蟻群算法（ACS）和ACS+3opt算法在三種不同規模的TSP上進行比較，對比本文算法與其他算法的收斂速度與結果。

3.1 實驗環境設置

本文實驗環境為：Windows 10操作系統，利用MATLAB 2018a進行仿真。為了驗證算法在各個規模TSP問題中的有效性，選擇分別與傳統蟻群算法ACS與ACS+3opt算法進行不同規模的TSP進行測試。同時選擇與目前最新的改進型蟻群算法文獻［9，10，18，19］進行對比，分析比較本文算法的改進。實驗中算法參數設置如表1所示。

3.2 與傳統算法對比結果

首先設置與ACS和ACS+3opt算法進行對比。將各個算法運行10次，比較每種算法在求解TSP時的最優解、平均解、最小誤差百分比與收斂時間。其中平均值向下取整，最小誤差百分比保留兩位小數，設置最大迭代次數為5 000，收斂時間為算法開始到最終收斂所用時間，以秒為單位。結果如表2所示。

通過對比可以看出本文算法在應對小規模問題時有很好的表現，在各個算例中均能找到最優解或與最優解之間最小誤差小于1%，并且可以看出實驗結果的平均解與最優解之間誤差較小，證明了算法的穩定性。在Eil51、Eil76等小規模問題上，ACS、ACS+3opt與ICACO均能找到最優路徑，但ICACO平均解的質量優于ACS、ACS+3opt。通過在更大規模旅行商問題上與基本蟻群算法的對比可以看出，隨著旅行商問題的規模增大，ACS、ACS+3opt的精度有所下降，而本文算法保持了很好的精度，最優解仍然保持在1%以內的精度，算法的最優解與平均解均優于ACS和ACS+3opt算法。在算法的收斂時間對比上，在小規模TSP問題eil51、eil76、rat99上ACS與ACS+3opt算法的收斂速度快于ICACO，隨著TSP的規模不斷增大到100以上時，由于動態分化策略能夠有效地加快收斂速度ICACO的收斂速度逐漸超過ACO與ACO+3opt，并且隨著問題規模的增大，ICACO的收斂速度也越來越高于ACO、ACO+3opt，這是由于隨著問題規模的增大ACO與ACO+3opt不可避免地陷入局部最優，導致算法的尋優能力不足，難以找到更優解，而ICACO由于存在鄰域誘導機制，可以幫助種群在大規模問題上更好地拓展解空間避免陷入局部最優。

3.3 與最新改進算法對比結果

為了保證實驗的客觀性，將ICACO與目前最新的改進算法在TSP上進行對比，對比結果如表3所示。表中“-”表示該文未做該實驗。由表3可以看出在與當今最新的算法比較時，本文算法仍然有很好的表現。在大中小規模的TSP問題中本文算法最優結果均優于其他算法，在各個問題中均能保證誤差在1%左右，隨著TSP問題的規模逐漸增大，許多算法已經無法找到結果并且平均解很差。本文算法在處理大規模問題時使用了孤立分化機制，大規模問題中各個算法往往難以避免陷入局部最優，本文算法通過加入誘導機制，在種群陷入局部最優后可以跳出局部最優，增加解的多樣性，提高解的質量從而找到更優解。其中部分實驗路徑結果如圖7所示。

3.4 與其他多種群蟻群算法對比

為了體現本文算法的有效性，本文選擇了其他多種群蟻群算法進行對比分析。其中文獻［13］為自適應分組蟻群算法，根據迭代情況將種群分為不同大小的種群，文獻［15］將螞蟻分為常規螞蟻和拓展螞蟻，分別負責搜索效率與搜索廣度。

通過表4可以看出，在各個小于100規模的TSP上本文算法性能都優于對比算法，在ch130數據集上最優路徑文獻［15］算法優于本文算法但本文算法的平均解優于文獻［15］算法。從表4可以看出， 由于文獻［13］算法只將螞蟻進行分組而未對其進行不同分工，導致算法解的精度不足，而ICACO將螞蟻動態分組，調整不同種群螞蟻的數量的同時設置不同的搜索路線和信息素釋放方式，保證兩種螞蟻相互合作，在加快算法收斂速度的同時提高解的質量。文獻［15］算法雖然將螞蟻進行不同分工，但并沒有提出跳出局部最優的機制，在算法后期容易陷入局部最優，降低解的精度，而ICACO通過鄰域誘導機制，在孤立蟻發現更優路線后將種群誘導至新路線附近，加強對新路線的搜索，在算法后期能夠很好地提高解的精度。

表4顯示了對比結果，缺失的數據用“-”代替。

3.5 算法性能分析

3.5.1 算法多樣性分析

為了證明本文算法增加解的多樣性的有效性，通過對比算法在處理TSP問題時每一代路徑的長度，對算法的多樣性進行分析。實驗結果如圖8所示。

通過對比算法在運行TSP時每一代路徑長度與總路徑長度可以看出，算法在陷入局部最優時，利用孤立分化策略增加解的多樣性，隨著算法后期不可避免地陷入停滯，孤立個體數也在不斷增大，算法的解空間也在逐漸增大，最終在算法4 500次迭代后找到了優化解，保證了算法在搜索后期能夠跳出局部最優找到更優解。

3.5.2 算法收斂性分析

為了比較算法在收斂速度上的提高，選擇在rand400、eil51兩個規模的TSP上與ACS、ACS+3opt算法進行實時收斂過程對比，為保證實驗準確性選擇相同數量的螞蟻數，在小規模問題的測試中將迭代次數設為5 000次，將大規模問題的最大迭代次數設為2 000次。實驗結果如圖9所示。

通過對比三種算法在大小兩個規模上的運行結果，可以看出本文算法在搜索初期就能很快收斂，最優路徑快速迭代，算法不斷找到更優解且具有較好的搜索能力。在大規模問題rd400上可以更明顯地看出，ACS、ACS+3opt算法在搜索初期就陷入了局部最優，而本文算法在搜索初期采用混沌初始化策略，有效避免了算法在初期陷入早熟。同時在搜索的后期可以看出ACS算法在迭代到一定次數以后便無法找到更優路徑，過早陷入局部最優使得在大規模問題時無能為力。而ACS+3opt算法仍不能避免算法在初期就陷入早熟，算法初期的多樣性較差，而在算法后期雖然有一定的跳出局部最優解的能力，但由于搜索能力不足同樣導致算法陷入局部最優。本文算法在每次迭代初始化時采用混沌隨機機制使搜索能力得到加強，同時引入孤立分化機制使迭代后期最優路徑長度仍能不斷下降，找到更優路徑，有較強的跳出局部最優能力使得算法面對大規模問題時有較強的魯棒性。通過對比三種算法的收斂結果，可以看出本文算法很好地平衡了收斂速度與精度，初期搜索結果快速下降，大大加快了搜索速度，同時后期可以有效地跳出局部最優提高解的精度。

3.5.3 改進策略有效性分析

為分析改進算法中各個策略的有效性，設置算法ICACO-1、ICACO-2與ICACO算法進行對比實驗，對每個改進策略進行有效性分析。對比算法使用策略如表5所示。通過在不同數據集上進行對比實驗，將結果總結在表6中。其中ICACO-1只使用鄰域誘導機制，不對螞蟻進行分化，所有螞蟻都設置為正常種群，當有螞蟻找到更優路徑后就會將所有螞蟻引至新路徑。ICACO-2只使用動態分化策略，將螞蟻分化為正常蟻與孤立蟻，不使用鄰域誘導策略進行信息素矩陣更新。

由表6可以看出，在小規模問題eil51、eil76、kroA100上ICACO、ICACO-1、ICACO-2均能找到最優解，而當數據集規模增大，ICACO-2在eil101、pr107、ch130數據集上的表現優于ICACO-1，表明將種群動態分化為正常蟻與孤立蟻能夠有效地拓展搜索范圍，使算法在搜索階段具有很好的性能。當數據集規模提升到400以上時算法容易陷入局部最優，而ICACO-1在kroA200、rd400、fl417、pr439數據集上的表現優于ICACO-2，表明鄰域誘導機制在大規模問題上能夠有效幫助算法避免陷入局部最優。而同時使用動態分化機制和鄰域誘導策略的ICACO由于孤立蟻的存在，在解的精度上比單獨使用正常蟻進行搜索的ICACO-1提高了50%左右。實驗結果ICACO在各個數據集上的表現都比單獨使用一種策略的算法優秀，表明動態分化機制和鄰域誘導策略能夠很好地幫助算法提高搜索能力。

3.5.4 算法復雜度分析

表7中n為節點數;m為螞蟻總數;m1為孤立螞蟻數;m2為正常種群個數;i為最大迭代次數。通過表7可知，ICACO的時間復雜度為O（i×n2×m），由此可以看出動態分化機制和鄰域誘導機制沒有額外增加算法的時間復雜度。

4 結束語

本文分析了現有蟻群算法與幾種改進蟻群算法，針對其不足之處提出了一種引入動態分化和鄰域誘導機制的雙蟻群優化算法。該算法首先將螞蟻位置和路徑上的信息素進行混沌隨機，加快了算法的搜索速度；其次通過孤立分化策略將螞蟻分為原始種群和孤立種群，提高了解的多樣性。實驗結果表明本文算法在TSP求解上效果良好，尤其針對大規模TSP時也具有很好的表現，但在更大規模的TSP上仍存在收斂速度慢等問題。下一步的研究方向是利用多種群博弈策略解決更大規模TSP。

參考文獻：

[1]Dorigo M， Maniezzo V， Colorni A. Ant system： optimization by a co-lony of cooperating agents［J］.IEEE Trans on Systems， Man， and Cybernetics， Part B，1996，26（1）：29-41.

［2]張宏宏，甘旭升，李雙峰，等.復雜低空環境下考慮區域風險評估的無人機航路規劃［J］.儀器儀表學報，2021，42（1）：257-266.（Zhang Honghong， Gan Xusheng， Li Shuangfeng， et al. UAV route planning considering regional risk assessment under complex low altitude environment［J］.Chinese Journal of Scientific Instrument，2021，42（1）：257-266.）

［3]李燚，唐倩，劉聯超，等.基于改進蟻群算法的汽車混流裝配調度模型求解［J］.中國機械工程，2021，32（9）：1126-1133.（Li Yan， Tang Qian， Liu Lianchao， et al. An improved ACO algorithm for automobile mixed-flow assembly scheduling problems［J］.China Mechanical Engineering，2021，32（9）：1126-1133.）

［4]包漢，祝海濤，劉迪.基于±3σ正態概率區間分族遺傳蟻群算法的移動機器人路徑規劃研究［J］.控制與決策，2021，36（12）：2861-2870.（Bao Han， Zhu Haitao， Liu Di. Path planning of a mobile robot based on ±3σ normal probability interval population division using the genetic ant-colony algorithm［J］.Control and Decision，2021，36（12）：2861-2870.）

［5]孫明杰，周林，于云龍，等.無人機自組網中基于蟻群優化的多態感知路由算法［J］.系統工程與電子技術，2021，43（9）：2562-2572.（Sun Mingjie， Zhou Lin， Yu Yunlong， et al. Ant colony optimization based polymorphism-aware routing algorithm for Ad hoc UAV network［J］.System Engineering and Electronics，2021，43（9）：2562-2572.）

［6]Pan Han， You Xiaoming， Liu Sheng， et al. Pearson correlation coefficient-based pheromone refactoring mechanism for multi-colony ant colony optimization［J］.Applied Intelligence，2020，51（2）：1-23.

［7]Dorigo M， Gambardella L M. Ant colony system： a cooperative lear-ning approach to the traveling salesman problem［J］.IEEE Trans on Evolutionary Computation，1997，1（1）：53-66.

［8]Stutzle T， Hoos H H. Max-min ant system［J］.Future Generation Computer Systems，2000，16（8）：889-914.

［9]陳佳，游曉明，劉升，等.結合信息熵的多種群博弈蟻群算法［J］.計算機工程與應用，2019，55（16）：170-178.（Chen Jia， You Xiao-ming， Liu Sheng， et al. Entropy-game based multi-population ant colony optimization［J］.Computer Engineering and Applications，2019，55（16）：170-178.）

［10]陳穎杰，高茂庭.基于信息素初始分配和動態更新的蟻群算法［J］.計算機工程與應用，2022，58（2）：95-101.（Chen Yingjie， Gao Maoting. Pheromone initialization and dynamic update based ant colony algorithm［J］.Computer Engineering and Applications，2022，58（2）：95-101.）

［11]陳佳，游曉明，劉升，等.動態分級的改良螞蟻算法及其應用研究［J］.計算機應用研究，2019，36（2）：380-384.（Chen Jia， You Xiao-ming， Liu Sheng， et al. Research on dynamic hierarchical ant optimization algorithm and its application［J］.Application Research of Computers，2019，36（2）：380-384.）

［12]張毅，權浩，文家富.基于獨狼蟻群混合算法的移動機器人路徑規劃［J］.華中科技大學學報：自然科學版，2020，48（1）：127-132.（Zhang Yi， Quan Hao， Wen Jiafu. Mobile robot path planning based on the wolf ant colony hybrid algorithm［J］.Huazhong University of Science & Technology：Natural Science Edition，2020，48（1）：127-132.）

［13]卜冠南，劉建華，姜磊，等.一種自適應分組的蟻群算法［J］.計算機工程與應用，2021，57（6）：67-73.（Bu Guannan， Liu Jianhua， Jiang Lei， et al. An ant colony algorithm with adaptive grouping［J］.Computer Engineering and Applications，2021，57（6）：67-73.）

［14]Gülcü瘙塁， Mahi M， BaykanK， et al. A parallel cooperative hybrid method based on ant colony optimization and 3-opt algorithm for solving traveling salesman problem［J］.Soft Computing，2018，22（5）：1669-1685.

［15]馮振輝，肖人彬.基于混合反饋機制的擴展蟻群算法［J］.控制與決策，2022，37（12）：3160-3170.（Feng Zhenhui， Xiao Renbin. Extended ant colony algorithm based on mixed feedback mechanism［J］.Control and Decision，2022，37（12）：3160-3170.）

［16]馬小陸，袁書生，王兵，等.均勻分布Logistic混沌序列的RRT路徑規劃算法研究［J］.機械科學與技術，2022，41（4）：610-618.（Ma Xiaolu， Yuan Shusheng， Wang Bing， et al. Research on RRT path planning algorithm for uniformly distributed Logistic chaotic sequence［J］.Mechanical Science and Technology for Aerospace Engineering，2022，41（4）：610-618.）

［17]梁杰，陳嘉豪，張雪芹，等.基于獨熱編碼和卷積神經網絡的異常檢測［J］.清華大學學報：自然科學版，2019，59（7）：523-529.（Liang Jie， Chen Jiahao， Zhang Xueqin， et al. One-hot encoding and convolutional neural network based anomaly detection［J］.Journal of Tsinghua University：Science and Technology Edition，2019，59（7）：523-529.）

［18]Tuani A F， Keedwell E， Collett M. Heterogenous adaptive ant colony optimization with 3-opt local search for the travelling salesman pro-blem［J］.Applied Soft Computing，2020，97（PB）：106720.

［19]Huang Yao， Shen Xiaoning， You Xuan. A discrete shuffled frog-leaping algorithm based on heuristic information for traveling salesman problem［J］.Applied Soft Computing，2021.102：107085.

收稿日期：2023-02-28；修回日期：2023-04-17

基金項目：國家自然科學基金資助項目（61673258，61075115）；上海市自然科學基金資助項目（19ZR1421600）

作者簡介：禹博文（1997-），男，河南鄭州人，碩士研究生，主要研究方向為智能算法、機器學習、人工智能；游曉明（1963-），女（通信作者），江蘇興化人，教授，碩導，博士，主要研究方向為群智能系統、分布式并行處理、進化算法（yxm6301@163.com）；劉升（1966-），男，湖北大冶人，教授，碩導，博士，主要研究方向為量子啟發式進化算法、分布式并行處理、進化算法.