坡度對爆炸沖擊波傳播影響的試驗研究?

陳 君 姬建榮 康 昊 李毅卓 葉希洋

西安近代化學(xué)研究所（陜西西安，710065）

0 引言

爆炸沖擊波對目標(biāo)的毀傷程度不僅與彈藥自身的威力有關(guān)，也與爆炸時的作用環(huán)境密切相關(guān)。 對于無限空氣介質(zhì)，爆炸沖擊波理論已有成熟的經(jīng)驗公式[1]。 而對于密閉或半密閉有限空間的沖擊波傳播理論，許多學(xué)者正在開展研究。

李秀地等[2]通過數(shù)值模擬開展長坑道中化學(xué)爆炸沖擊波壓力的傳播規(guī)律研究。 張玉磊等[3]通過試驗研究半密閉環(huán)境下方形坑道內(nèi)爆炸沖擊波的傳播規(guī)律。 趙新穎等[4]通過仿真和試驗的方法研究密閉環(huán)境下溫壓炸藥爆炸沖擊波在爆炸堡內(nèi)的傳播規(guī)律。 楊亞東等[5]通過建立長方體密閉結(jié)構(gòu)內(nèi)爆炸沖擊波傳播和疊加分析模型研究內(nèi)爆炸沖擊波的分布特性。

可以看到，學(xué)者們主要通過仿真和試驗等途徑進行了半密閉、密閉環(huán)境的爆炸沖擊波傳播規(guī)律研究。 野外實戰(zhàn)中，場景地面多為起伏不平的山地。研究爆炸沖擊波實戰(zhàn)地形下的傳播規(guī)律對野外實戰(zhàn)防護和毀傷評估具有現(xiàn)實意義。 唐建曾[6]通過激波管研究了坡地對沖擊波傳播規(guī)律的影響。 而對于野外坡地對沖擊波傳播影響研究國外未見報道。

本文中，在試驗場構(gòu)建不同坡度的斜坡地形，在斜坡上布設(shè)超壓測點，獲取不同坡度的斜坡地面測點處的沖擊波超壓，研究斜坡地形對沖擊波傳播的影響，為實戰(zhàn)防護和毀傷評估提供技術(shù)支持。

1 試驗

1.1 試驗布局

在試驗場構(gòu)建了相同寬度、不同坡度的斜坡地形。 坡度θ分別為0°（平整地面）、 ±10°、 ±20°、 ±30°。 在距坡頭2.50 m 處的硬質(zhì)水平地面布設(shè)梯恩梯（TNT）球形藥作為爆炸源。 在距爆炸源行程距離L為2.05、2.35、2.65、2.95、3.25、3.75、4.25、4.75、5.25、5.75、6.75 m 處布設(shè)11 個超壓測點，獲取斜坡各處的沖擊波超壓p。

試驗布局如圖1 所示。

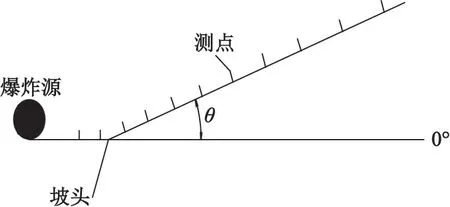
圖1 試驗布局示意圖Fig.1 Test layout

1.2 爆炸源

爆炸源為TNT 壓制而成的球形裸藥。 在球形爆炸源中心開孔，采用15 g 的JH14（炸藥型號）作為傳爆藥，用微型導(dǎo)爆索起爆球形TNT。 球形爆炸源的密度為（1.58 ±0.02） g/cm3，藥量為（5.00 ±0.08） kg。 為了避免爆炸過程中地面炸坑能量消耗對試驗結(jié)果的影響，試驗前將球形TNT 爆炸源放置在與地面平齊的Q235 鋼板（20 mm 厚）上起爆。

爆炸源結(jié)構(gòu)及布設(shè)如圖2 所示。

圖2 爆炸源結(jié)構(gòu)及布設(shè)圖Fig.2 Structure and layout of the explosion source

1.3 超壓測試系統(tǒng)

超壓測試系統(tǒng)由壁面沖擊波超壓傳感器、低噪聲信號線、ICP 信號調(diào)理器、數(shù)據(jù)采集器等組成。 壁面沖擊波超壓傳感器的感應(yīng)面與斜坡面平齊，即與水平面的角度與坡度相同。 傳感器型號為113B26，美國PCB 公司，量程3.5 MPa。 數(shù)據(jù)采樣頻率設(shè)置為1 MHz，系統(tǒng)帶寬大于100 kHz。

2 結(jié)果與分析

2.1 坡度對超壓峰值的影響

同工況進行了多發(fā)試驗，對試驗數(shù)據(jù)求平均值。圖3 為坡頭前2 個、坡頭后3 個測點處的超壓峰值對比曲線。

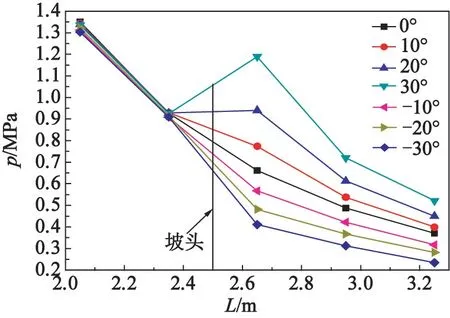
圖3 不同測點處的超壓峰值對比Fig.3 Comparison of the peak overpressure at different measuring points

由圖3 可以看出:在坡頭之前，不同工況時，2個測點的超壓峰值相差不大；在坡頭之后，上坡超壓峰值相比平地時明顯增大，且隨坡度的增大而增大；下坡超壓峰值相比平地時明顯減小，且隨坡度絕對值的增大而減小。 隨著坡度的變化，超壓峰值在坡頭區(qū)域發(fā)生明顯變化。

圖4 為斜坡上各測點處的超壓峰值對比。

圖4 斜坡上各測點的超壓峰值隨行程的變化Fig.4 Variation of peak overpressure at different measuring points on the slope with distance

由圖4 可以看出:在上坡（θ＝10°、20°、30°）情況下，斜坡上測點的超壓峰值都會增大，且峰值會隨著坡度的增加而增加，隨著行程的增大而減小；相反，在下坡（θ＝-10°、-20°、-30°）情況下，超壓峰值會隨著下坡角度絕對值的增加而減小，隨著行程的增大而減小。 這一結(jié)論與文獻[6]的結(jié)果一致。文獻[6]中，利用激波管在不同的迎坡角下獲取的大量數(shù)據(jù)表明了激波沿地形變化的一般規(guī)律:沖擊波遇到迎坡時，坡面超壓增大；遇到負(fù)坡時，超壓峰值減小。 杜紅棉等[7]提出，當(dāng)空氣中傳播的沖擊波遇到剛性壁面時，質(zhì)點速度驟然變?yōu)榱悖诿嫣庂|(zhì)點不斷聚集，使壓力增加。 趙新穎等[4]認(rèn)為，沖擊波在有限空間遇到固體壁面會形成反射，在特定位置會出現(xiàn)聚焦現(xiàn)象，使沖擊波超壓峰值增加。 與本文的結(jié)論一致。 綜上，同類型、同質(zhì)量的炸藥觸地爆炸，由于坡度地形的影響，壓力峰值與坡度有關(guān)。

為了研究斜坡地形時沖擊波超壓峰值增大或減小的程度，將斜坡測點的超壓峰值與相同行程處測點的平地超壓峰值作比值，獲得超壓峰值比。 超壓峰值比隨行程的變化曲線，如圖5 所示。

圖5 超壓峰值比隨行程的變化Fig.5 Variation of peak overpressure ratio with distance

由圖5 可以看出:上坡時，超壓峰值比（超壓增大程度）隨上坡坡度的增大而增大，也就是上坡坡度越大，超壓峰值增大程度越大。 上坡時，超壓峰值比呈現(xiàn)為振蕩變化趨勢:先增大，后減小，再增大，最后趨于平穩(wěn)。 下坡時，超壓峰值比隨下坡坡度絕對值的增大而減小。 下坡時，超壓峰值比同樣表現(xiàn)為振蕩變化趨勢:先減小，再增大，再減小，最后趨于平穩(wěn)。 這可能是沖擊波遇到斜坡后空氣域突變或放射等因素所致。

文獻[6]中，通過激波管試驗數(shù)據(jù)獲得了斜坡處超壓峰值的經(jīng)驗公式。

上坡經(jīng)驗公式:

式中:△pθ為斜坡處超壓峰值；η＋為增壓系數(shù)（超壓比）；△p為入射壓，0.01 MPa≤△p≤0.60 MPa。θ為坡度；A、B分別為系數(shù)。

下坡經(jīng)驗公式:

式中:η_為減壓系數(shù)。

由式（1）～式（4）可以看出，增壓系數(shù)（超壓比）是隨坡度變化的二次函數(shù)。 式（5）～式（6）表明，減壓系數(shù)在0°≤θ≤20°時只與坡度相關(guān)，且是隨坡度變換的指數(shù)衰減函數(shù)；在20° ＜θ≤90°時，是只與坡度相關(guān)的二次函數(shù)。

文獻[6]中的經(jīng)驗公式與圖5 中的曲線變化趨勢有差異。 用20°上坡試驗數(shù)據(jù)驗證發(fā)現(xiàn)，式（1）～式（4）獲得的增壓系數(shù)整體偏大，偏差范圍16%～80%。 用-20°下坡試驗數(shù)據(jù)驗證發(fā)現(xiàn)，式（5）～式（6）獲得的減壓系數(shù)多數(shù)偏小，偏差在-25%～7%之間。 -30°下坡試驗數(shù)據(jù)驗證結(jié)果同樣偏小，偏差在-22%～-8%之間。 這可能與試驗條件相關(guān)。

爆炸沖擊波傳播的研究更多關(guān)注的是對比距離、坡度和斜坡超壓之間的關(guān)系。 根據(jù)試驗數(shù)據(jù)，擬合了對比距離、坡度θ與增（減）壓系數(shù)η的關(guān)系，三維結(jié)果如圖6 所示。

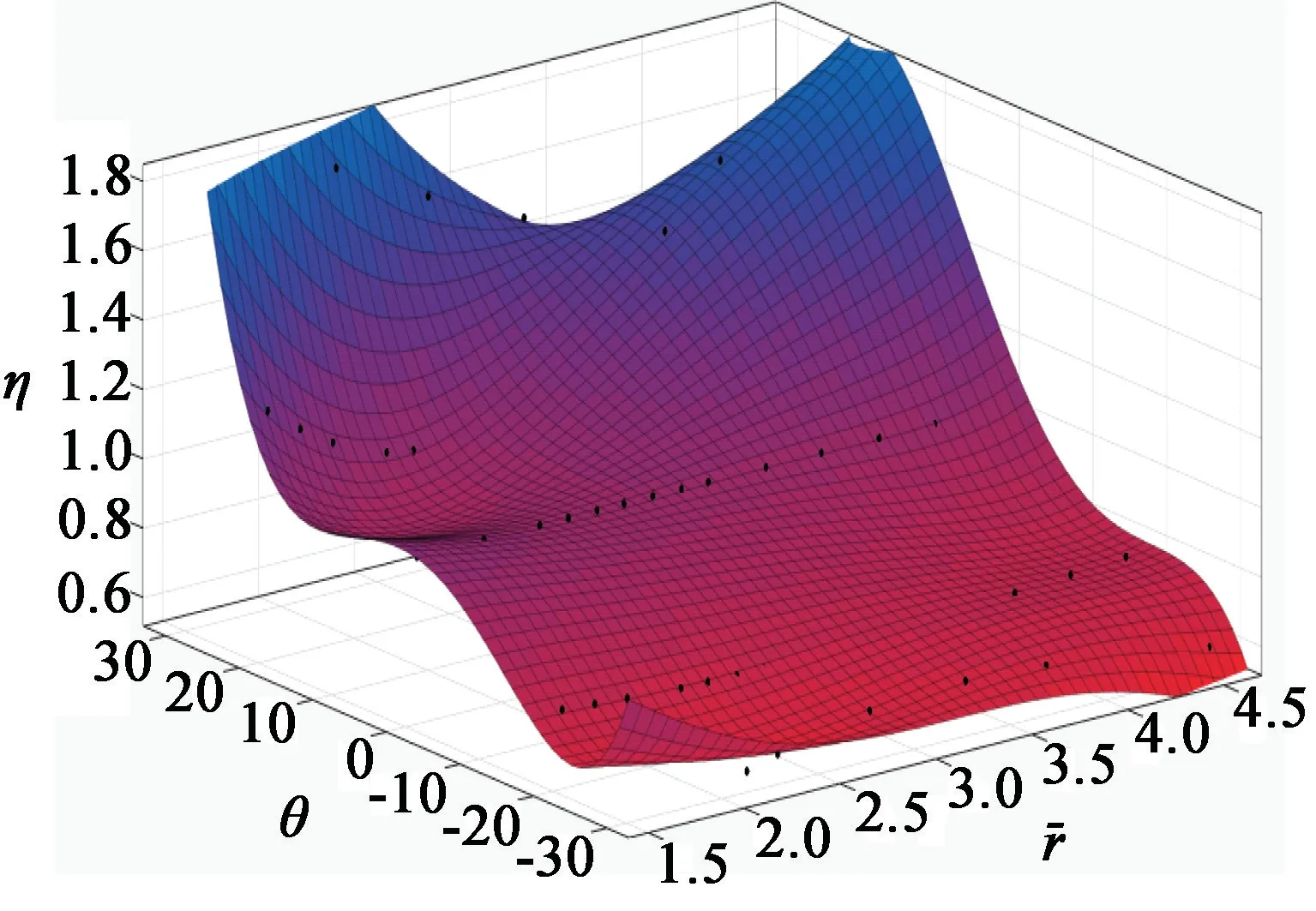
圖6 增（減）壓系數(shù)與對比距離和坡度的關(guān)系Fig.6 Relationship between η andor θ

式中:η（，θ）為增（減）壓系數(shù)；為對比距離；θ為斜坡坡度。

式（7）為增（減）壓系數(shù)與對比距離和坡度的關(guān)系，擬合結(jié)果與試驗結(jié)果偏差-6.08%～7.29%。

2.2 坡度對超壓峰值到達時間的影響

圖7 為坡頭前2 個測點、坡頭后1 個測點處超壓峰值到達時間的對比曲線。 由圖7 可以看出:沖擊波遇到斜坡前，超壓峰值到達時間與通過平地時相比變化不大；上坡后，超壓峰值到達時間減小；下坡后，超壓峰值到達時間增大。

圖7 不同測點處超壓峰值到達時間的對比Fig.7 Comparison of the arrival time of peak overpressure at different measuring points

圖8 為斜坡上各測點超壓峰值到達時間的對比。 由圖8 可以看出:上坡時，超壓峰值到達時間隨坡度的增大而減小，隨著行程的增大而增大，行程越大，區(qū)分越明顯；下坡時，超壓峰值達到時間隨著坡度絕對值的增大而增大，隨著行程的增大而增大，行程越大，區(qū)分越明顯。 通過試驗數(shù)據(jù)，對不同坡度時超壓峰值到達的時間比的均值進行擬合，得到了αθ與θ的近似關(guān)系:

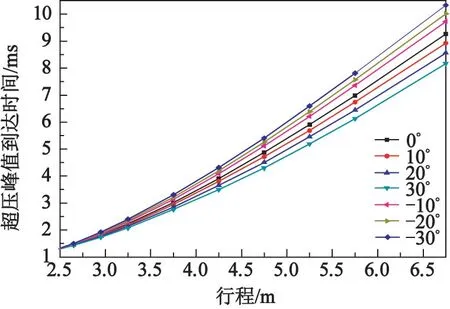
圖8 斜坡上各測點超壓峰值到達時間的對比Fig.8 Comparison of the arrival time of peak overpressure at different measuring points on the slope

式中:tθ為坡度為θ時超壓峰值的到達時間；t0為坡度為0°時超壓峰值的到達時間；αθ為超壓峰值到達的時間比；θ為斜坡坡度。

2.3 坡度對超壓脈寬的影響

圖9 為平地和20°、-20°斜坡相應(yīng)行程測點處的超壓脈寬的對比。 從圖9 中可以看出，相比平地，上坡時超壓脈寬變小，下坡時超壓脈寬增大。 脈寬的變化整體表現(xiàn)為振蕩趨勢。

圖9 不同坡度時各測點處的脈寬Fig.9 Pulse width at different measuring points at different slopes

2.4 坡度對超壓沖量的影響

圖10 給出了平整地形和20°、-20°坡度斜坡時相應(yīng)測點處沖量大小的比較。 從圖10 中可以看出，坡頭前、后上坡時沖量增大，下坡時沖量減小。 沖擊波過坡頭后，沖量同樣表現(xiàn)為上坡增大、下坡減小的趨勢，沖量變化呈振蕩趨勢。

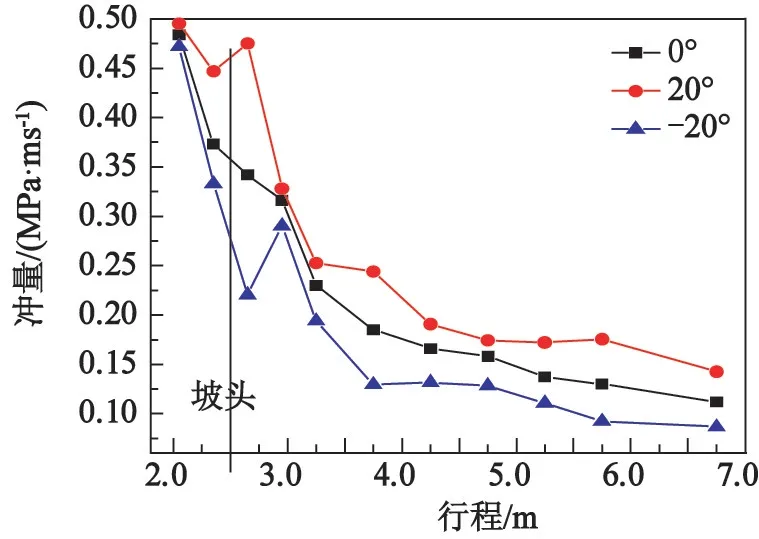
圖10 不同坡度時各測點處的沖量Fig.10 Impulse at different measuring points at different slopes

3 結(jié)論

1）在坡頭之前的斜坡平整段處，沖擊波超壓峰值、超壓峰值到達時間與平地時的數(shù)據(jù)相當(dāng)。

2）從坡頭前測點開始，上坡超壓沖量增大，且隨坡度增大而增大；下坡超壓沖量減小，且隨坡度絕對值的增大而減小。

3）上坡時，超壓峰值和沖量比平地時的數(shù)據(jù)增大，超壓峰值和沖量隨坡度的增大而增大，超壓峰值和沖量的增大程度呈現(xiàn)振蕩變化趨勢；下坡時，超壓峰值和沖量比平地時的數(shù)據(jù)減小，超壓峰值和沖量隨下坡坡度絕對值的增大而減小，超壓峰值和沖量的減小程度呈現(xiàn)振蕩變化趨勢。

4）上坡時，超壓峰值到達時間比平地時的數(shù)據(jù)減小，超壓峰值到達時間隨上坡坡度增大而減小；下坡時，峰值到達時間比平地時的數(shù)據(jù)增大，超壓峰值到達時間隨下坡坡度絕對值的增大而增大。

5）超壓脈寬上坡時減小，下坡時增大。

6）得出不同坡度地形時沖擊波超壓峰值、超壓峰值到達時間與平整地面時相應(yīng)值的關(guān)系式；在本文給出的條件范圍內(nèi)，可用于工程實際計算。