基于UKF的六維力傳感器重力補償算法研究

李非凡,羅楊宇,曹志勇,李 翔,程 光

(1.北京聯合大學 城市軌道交通與物流學院,北京 100101;2.中國科學院自動化研究所,北京 100190;3.北京聯合大學 前沿智能技術研究院,北京 100101)

0 引言

隨著科學技術的發展,傳感器技術已經廣泛應用于機器人、航空航天、制造業、醫療設備等領域。在工業生產和科學研究中,力傳感器發揮著關鍵作用,特別是在人機交互領域中,精確測量物體的力和扭矩是確保人機交互系統精準控制和操作的關鍵[1]。在力控制、力反饋中,精確的力測量可以確保人機交互系統的安全性和可靠性,并且可以提高人機交互系統的操作精度和效率[2]。在人機交互系統中,為了實時監測機器人末端工具所受的力,通常在末端工具與機器人之間安裝六維力傳感器,可實時測量工具所受的三維力和力矩。隨著機器人的不斷運動,位姿信息不斷改變,受末端工具的重力影響,傳感零位值不斷變化,導致傳感器測量上產生一定偏差,降低了測量精度,進而影響機器人的操作。因此,有必要對機器人運動中的六維力傳感器進行重力補償與校正,使傳感器在機器人運動過程中也能檢測出末端工具實際所受的外力大小,從而使系統能夠更加精密地完成操作任務。六維力傳感器具有高靈敏度和高精度,對環境中的干擾和噪聲非常敏感[3]。因此,在處理六維力傳感器數據時,還需要采用一些有效的濾波和校準技術,以便最大限度地減小測量誤差和噪聲。

常用的六維力傳感器重力補償和校正算法包括線性回歸、最小二乘法、小波變換、神經網絡和粒子群優化等方法[4]。其中,利用線性回歸和最小二乘法計算傳感器的偏移量和靈敏度系數來進行重力補償和校正的方法具有計算簡單、易于實現等優點。小波變換方法將傳感器測量值分解為多個頻段,并分別進行重力補償和校正,從而有效地消除了高頻噪聲的影響[5]。神經網絡和粒子群優化方法可以根據傳感器的測量值和理論模型,通過自適應學習和優化來進行重力補償和校正,因此,具有較好的準確性和魯棒性。

這些算法在處理六維力傳感器的重力補償和校正時仍然存在不足之處。例如:算法的精度和準確性容易受到環境和傳感器位置的影響[6];部分算法需要進行多次試驗和復雜的參數調節,時間成本較高;部分算法對非線性和復雜的傳感器模型的處理能力有限,需要進一步研究和優化[7]。為解決上述問題,本文使用 UKF 算法處理六維力傳感器數據,以實現對六維力傳感器數據的高精度估計。

1 UKF 原理與算法設計

1.1 UKF 原理

UKF 是一種基于卡爾曼濾波器的無模型參數濾波器,可以用于估算非線性系統的狀態和參數。UKF算法是利用UT變換獲取Sigma點集合,這些Sigma點通過非線性系統進行傳播,以獲得一組新的預測Sigma點,再將預測的Sigma點通過觀測模型傳遞,以獲得一組預測測量。這組預測測量可以用來計算卡爾曼增益并更新狀態的均值和協方差矩陣,從而更新狀態估計[8]。通過非線性函數傳遞,將非線性函數線性化問題轉換成系統狀態量概率密度分布的近似,然后基于Kalman算法框架進行濾波。相較于傳統的卡爾曼濾波器,UKF 不需要對非線性系統進行線性化處理,能夠更好地處理非線性系統和噪聲,具有更好的魯棒性和準確性[9]。

1.2 UKF 算法設計流程

UKF 處理六維力傳感器數據的過程與一般的 UKF 處理過程類似,主要包括以下步驟:

1)狀態變量的選取:確定狀態向量,包括估計需要的物理量,即六維力數據。

2)建立狀態轉移函數:建立狀態轉移函數,將當前狀態向量映射到下一時刻的狀態向量。

3)建立測量函數:根據傳感器的測量原理,建立測量函數,將狀態向量映射到測量向量。

4)噪聲模型:確定噪聲模型,包括過程噪聲和測量噪聲,通常假設為高斯分布。

5)初始狀態的設定:根據實際情況,設定初始狀態向量和協方差矩陣。

6)Sigma 點的生成:根據當前狀態向量和協方差矩陣,生成Sigma點集合。Sigma點的數量通常為2n+1個,其中n是狀態向量的維數。

7)Sigma 點的傳播:根據狀態轉移函數,將 Sigma 點集合進行狀態轉移,得到預測的Sigma點集合。這些點的傳播過程采用無跡變換,以保持Sigma點的高斯分布特性。

8)預測狀態向量和協方差矩陣:從預測Sigma點集合中,計算預測狀態向量和協方差矩陣。

9)預測測量向量和協方差矩陣:將預測狀態向量和協方差矩陣通過測量函數得到預測測量向量和協方差矩陣。

10)狀態預測:使用當前狀態的均值和協方差矩陣生成一組Sigma點,通過非線性系統進行傳播,得到一組新的預測Sigma點,從預測的Sigma點計算出預測的狀態均值和協方差矩陣。

11)測量預測:將預測的Sigma點通過觀測模型傳遞,得到一組預測測量。這組預測測量可以用來計算卡爾曼增益。

12)計算卡爾曼增益:卡爾曼增益將預測的狀態估計與實際觀測進行比較。UKF使用基于預測狀態的均值和協方差矩陣、測量的均值和協方差矩陣以及預測測量的協方差矩陣計算卡爾曼增益。

13)更新狀態估計:通過卡爾曼增益和測量值來更新狀態的均值和協方差矩陣,將產生一個新的狀態估計值,該值可用于下一次迭代的預測步驟[10]。

2 基于六維力傳感器的 UKF 算法設計

2.1 設置參數

2.1.1設置狀態向量x

狀態向量x包含了末端受力工具(機械手)在X、Y、Z3個方向上的位置、受力、力矩等信息,表示為

x=[fx,fy,fz,mx,my,mz]T。

(1)

其中,fx,fy,fz表示機器人在X、Y和Z軸上的受力,mx,my,mz表示機器人圍繞X、Y和Z軸的力矩。

在 UKF 算法中,狀態向量x的更新是通過對x進行預測和校正來實現的。預測階段通過系統動態方程對x進行預測,校正階段通過測量方程對預測值進行校正。

2.1.2設置狀態噪聲Q

狀態噪聲Q表示系統動態方程中的噪聲,它可以通過狀態轉移矩陣G和通常假設為零均值的高斯白噪聲QwGT計算得到:

Q=GQwGT。

(2)

其中,G是狀態轉移矩陣。Q是噪聲方差矩陣。QwGT通常假設為零均值的高斯白噪聲,即:

Qw～N(0,Qw)。

(3)

其中,Qw是噪聲方差。

2.1.3設置測量噪聲R

測量噪聲R表示測量方程中的噪聲,它可以通過測量轉移矩陣G和測量方差R0計算得到:

R=GR0GT。

(4)

其中,G是測量轉移矩陣,R0是測量方差矩陣。

2.1.4設置無跡變換參數α,β,κ

UKF 算法中的無跡變換(Unscented Transformation)將高斯分布的均值和協方差轉換為一組樣本點,用于對非線性函數進行逼近[11]。

無跡變換需要設置3個參數:α,β,κ。其中,α控制樣本點離均值的距離,β用于處理高斯分布的不確定度,κ用于調整樣本點的權重。六維力傳感器UKF的算法取值為:α=0.001,β=2,κ=0。

2.2 預測階段

預測階段通過狀態轉移方程對狀態向量x進行預測,得到預測狀態向量xk|k-1和預測協方差矩陣Pk|k-1:

xk|k-1=f(xk|k-1),

(5)

(6)

其中,f是狀態轉移方程,Qk-1是狀態噪聲協方差矩陣。

2.3 校正階段

校正階段通過測量方程對預測狀態向量xk|k-1進行校正,得到校正狀態向量xk|k和校正協方差矩陣Pk|k:

yk=h(xk-1|k-1),

(7)

xk|k=xk|k-1+Kk(yk-h(xk|k-1)),

Pk|k=(I-KkHk)Pk|k-1。

其中,yk是測量向量,h是測量方程,Sk是測量殘差的協方差,Rk是測量噪聲協方差矩陣,Hk是測量轉移矩陣。

在 UKF 算法中,根據預測狀態向量xk|k-1和預測協方差矩陣Pk|k-1,可以通過無跡變換計算一組樣本點,然后根據這些樣本點和權重系數計算校正狀態向量xk|k和校正協方差矩陣Pk|k。

根據預測狀態向量xk|k-1和預測協方差矩陣Pk|k-1,計算一組無跡變換的樣本點:

(8)

(9)

接下來計算預測測量向量yk|k-1和預測測量協方差矩陣Pyy,k|k-1:

(10)

(11)

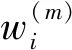
最后,計算校正增益Kk、校正狀態向量xk|k-1和校正協方差矩陣Pk|k:

xk|k=xk|k-1+Kk(yk-yk|k-1),

(12)

(13)

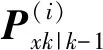
3 實驗過程

本實驗采用六維力傳感器KWR 75,采樣頻率為 1 000 Hz,該傳感器具有高靈敏度和高穩定性,能夠實時采集目標物體在6個自由度方向上的受力信息。實驗裝置如圖 1 所示,機械臂采用睿爾曼RM-65六自由度機械臂,末端工具采用因時仿人機械手。六維力傳感器通過法蘭安裝在機械臂與機械手之間,通過傳感器測量機械手與外界物體接觸的力和力矩,利用 Visual Studio Python語言實時接收數據并代入UKF算法中,導出實驗數據并繪制數據曲線圖。實驗通過采集末端機械手動態空載下六維力傳感器的測量數據,利用 UKF 算法對數據進行處理,驗證 UKF 算法的準確性和魯棒性。

實驗過程中,在末端工具不接觸外力與外界的環境下,對機械臂進行加速度和角速度激勵,記錄測量到的六維力的值[12]。圖 2～7 為力反饋的原始數據,橫軸為時間,單位為s,縱軸為力或力矩,單位為 N 或 N·m 。其中,圖2表示物體在X方向上的力,圖 3 表示物體在Y方向上的力,圖 4 表示物體在Z方向上的力,圖 5 表示物體在X方向上的力矩,圖 6 表示物體在Y方向上的力矩,圖7表示物體在Z方向上的力矩。

在未對力反饋數據做任何處理時,由于末端機械手重力的影響,在空載情況下,即在末端機械手不與外界物體接觸的情況下,六維力傳感器傳輸的力反饋數據不為 0,誤差較大,誤差范圍在 0～6 N之間。其中,X方向上力的誤差范圍在0～3 N之間,Y方向上力的誤差范圍在 0～2 N之間,Z方向上力的誤差范圍在0～6 N之間,X方向上力矩的誤差范圍在 0～1 N·m之間,Y方向上力矩的誤差范圍在 0～1 N·m之間,Z方向上力矩的誤差范圍在 0～1 N·m之間。

在上述實驗過程中,輸出同一時刻經UKF算法補償后的六維力傳感器數據,實驗結果如圖8～13所示。其中,圖8表示傳感器在X方向上所受的力,圖9表示傳感器在Y方向上所受的力,圖10表示傳感器在Z方向上所受的力,圖11表示傳感器在X方向上的力矩,圖12表示傳感器在Y方向上的力矩,圖13表示傳感器在Z方向上的力矩。

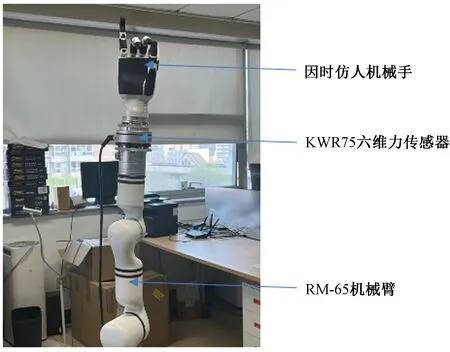
圖1 實驗裝置圖

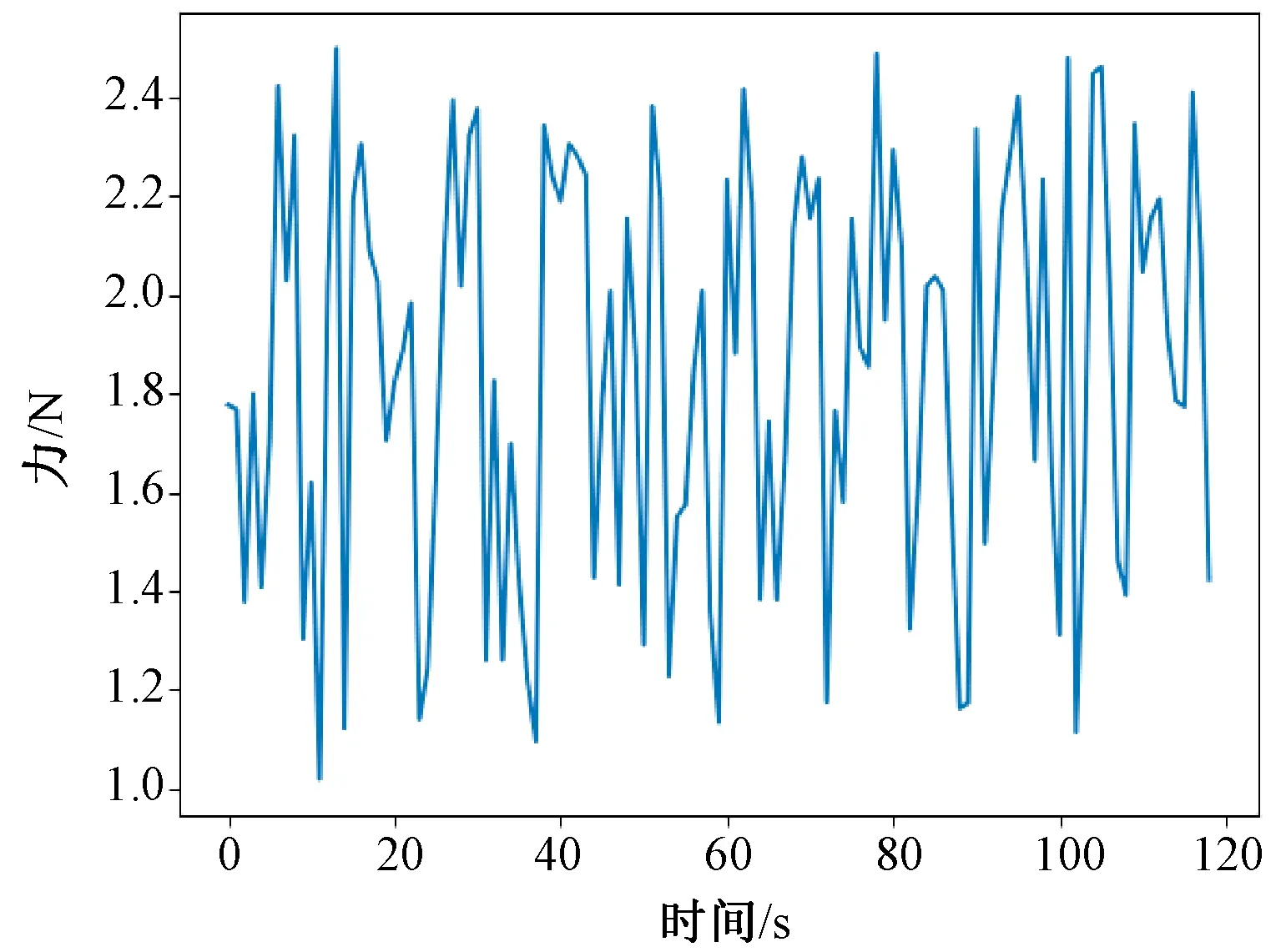
圖2 X軸力

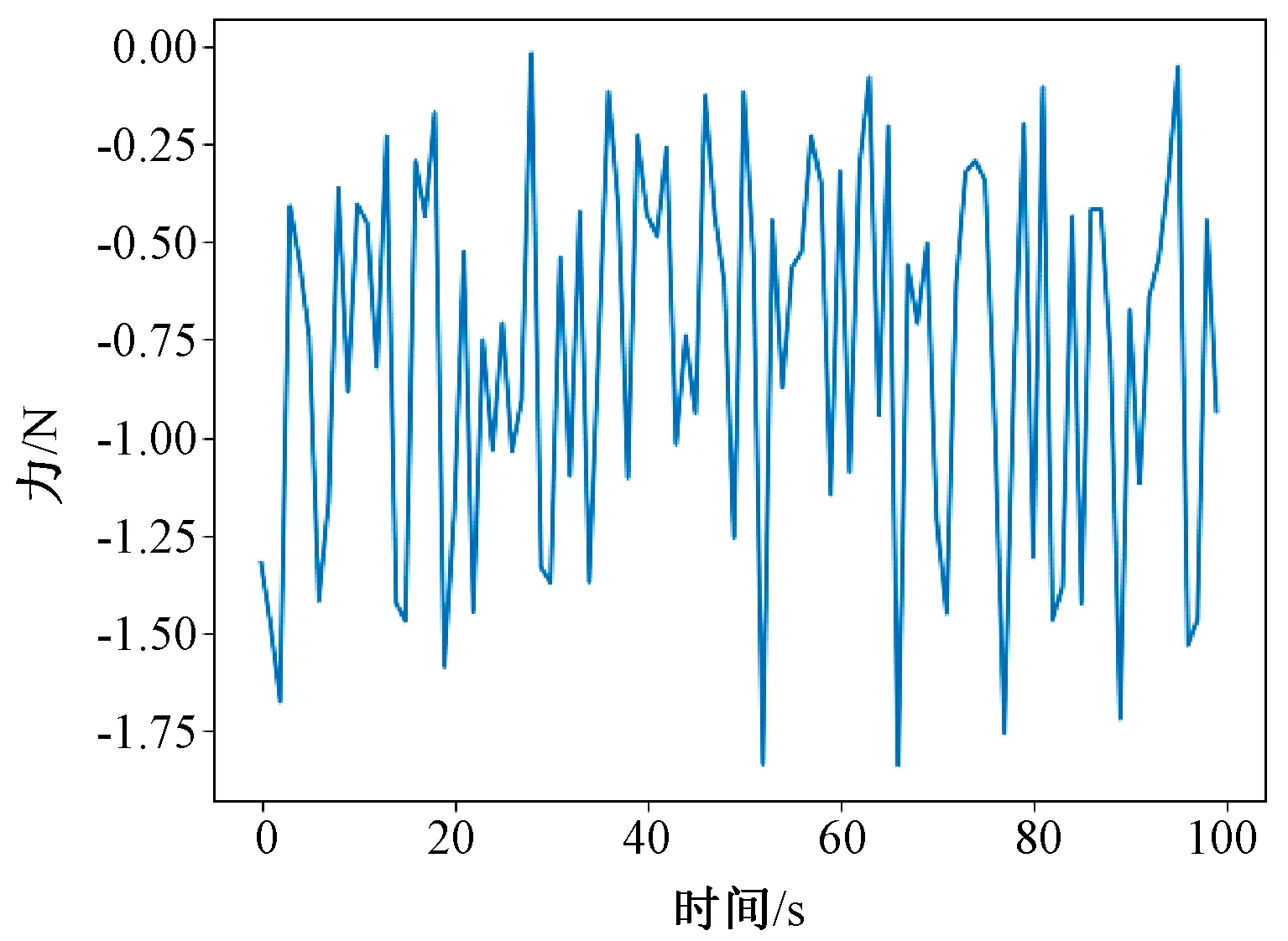
圖3 Y軸力

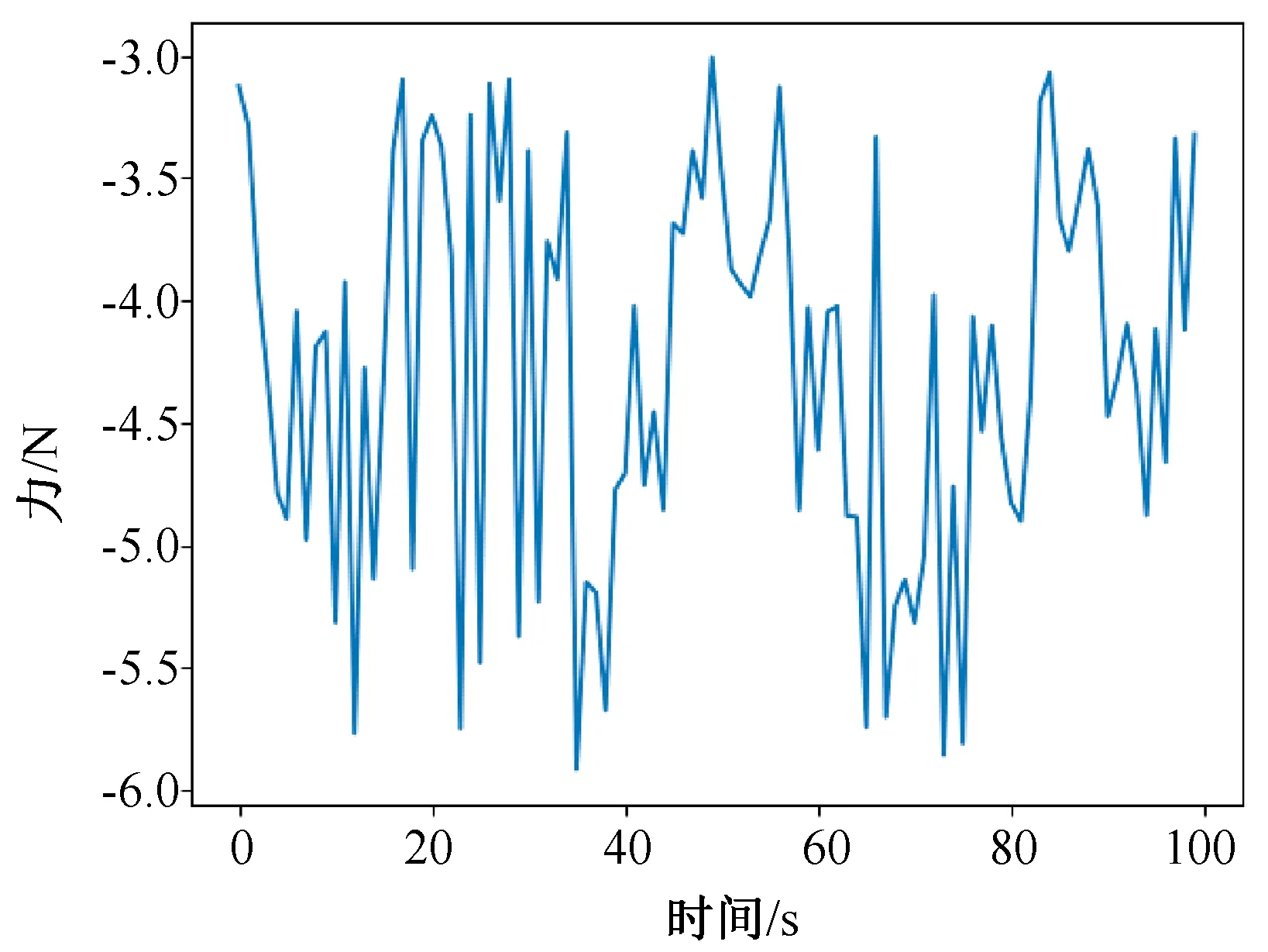
圖4 Z軸力

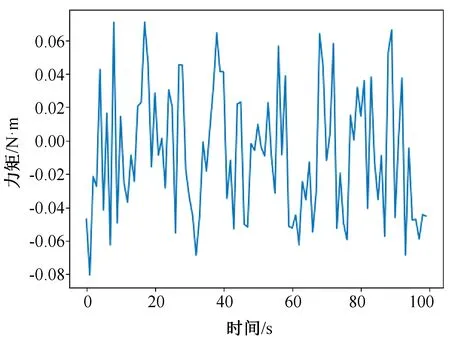
圖5 X軸力矩

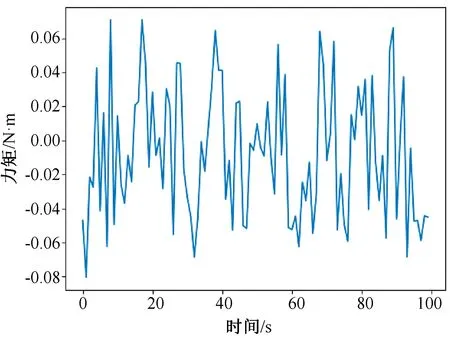
圖6 Y軸力矩

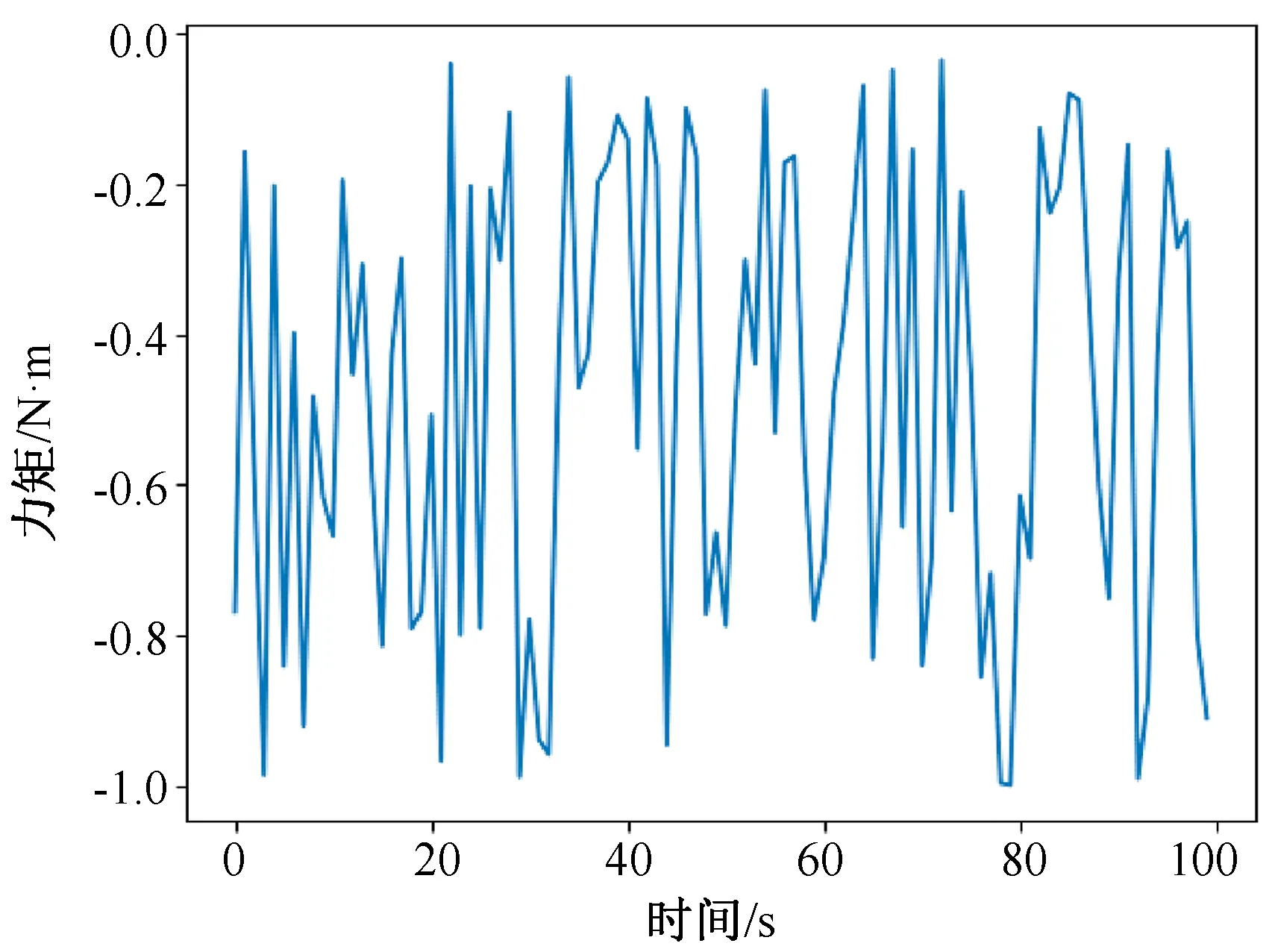
圖7 Z軸力矩

圖8 X軸受力

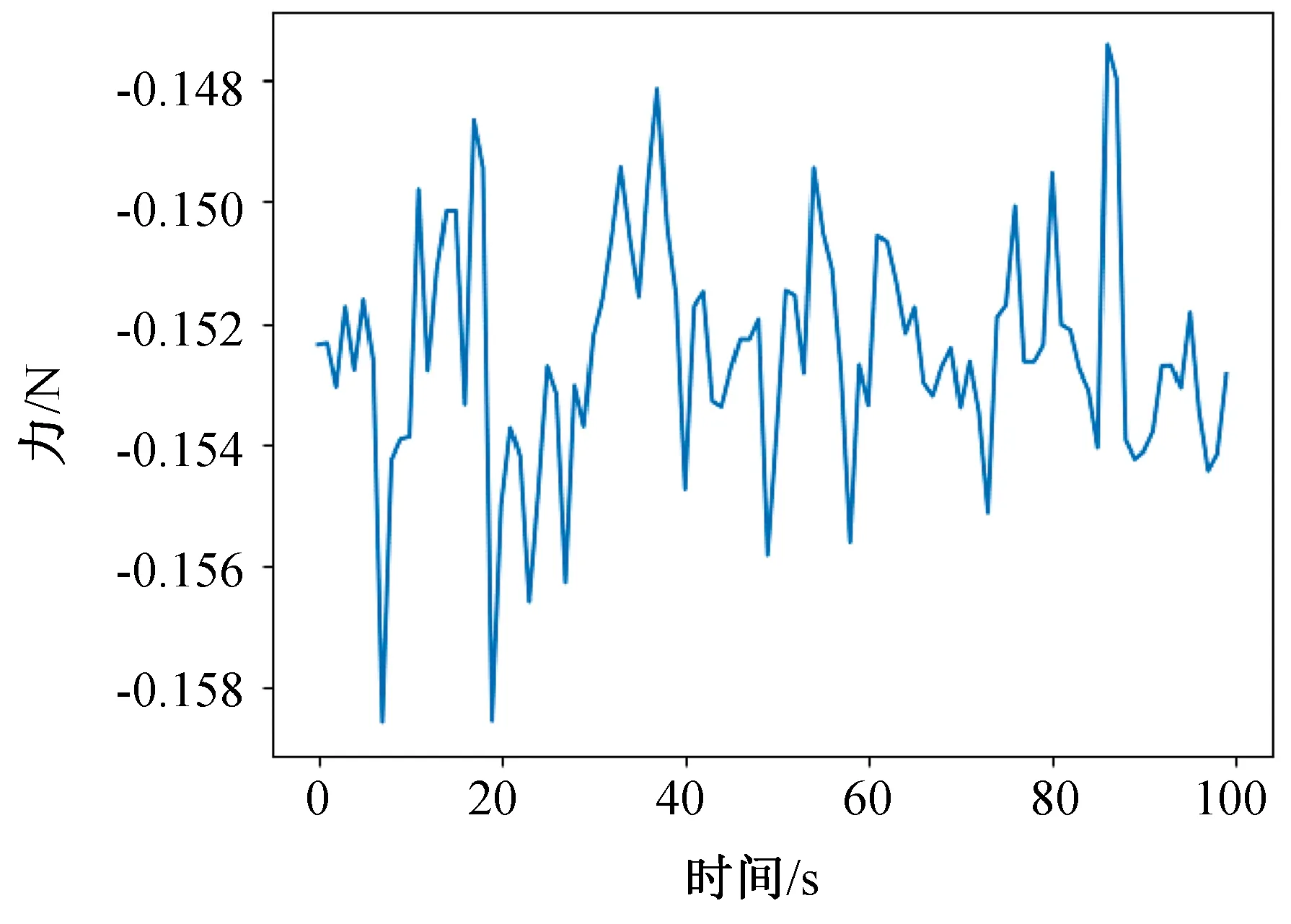
圖9 Y軸受力

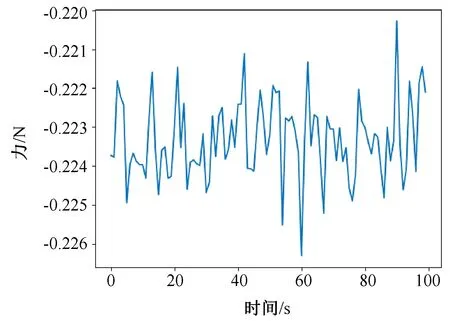
圖10 Z軸受力

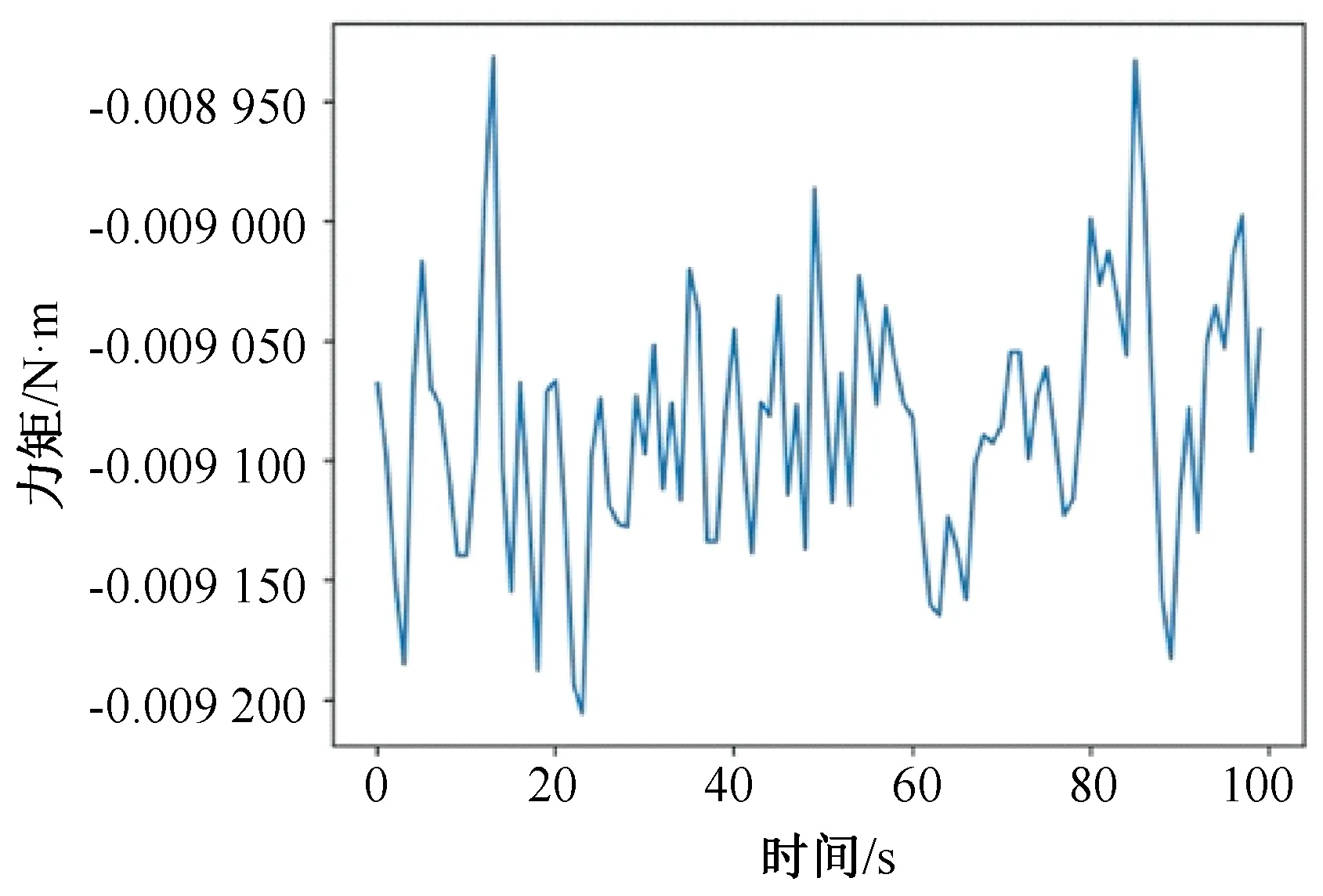
圖11 X軸力矩

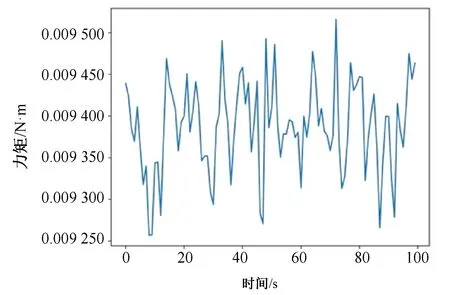
圖12 Y軸力矩

圖13 Z軸力矩

從圖 8～13 中可以看出,利用 UKF 算法補償處理后得到的力反饋數據的結果誤差更小,接近于 0,誤差范圍在 0～0.175 N 之間,其中X方向上力的誤差范圍在0～0.162 N 之間,Y方向上力的誤差范圍在0～0.160 N 之間,Z方向上力的誤差范圍在0～0.227 N 之間,X方向上力矩的誤差范圍在0～0.010 N·m之間,Y方向上力矩的誤差范圍在0～0.010 N·m 之間,Z方向上力矩的誤差范圍在0～0.039 N·m之間。

從圖 2～13 中可以看出:利用 UKF 算法處理后的數據結果偏差更小、更穩定。這表明 UKF 算法在處理六維力傳感器數據時具有更高的精度和更好的魯棒性,可以有效提高數據的準確性和可靠性。

4 結論

本文針對由機器人末端工具帶來的重力影響導致六維力傳感器數據不準確的問題,提出利用UKF算法對數據進行補償處理。本文通過實驗驗證說明使用 UKF 算法處理后的力反饋數據誤差更小、更平滑,偏差更小、更穩定。這表明UKF算法在處理六維力傳感器數據時,能夠有效提高數據的準確性和可靠性。本文通過實驗驗證了 UKF 算法在處理六維力傳感器數據時的優越性。在未來研究中,我們可以進一步探索 UKF 算法在其他機器人中的應用,例如,機器人的姿態估計、軌跡跟蹤等領域。同時,我們也可以探索使用其他更為先進的算法對六維力傳感器數據進行處理和應用,以期進一步提高機器人系統的性能和精度。