軸向運動分數階粘彈性梁的動力學模型及振動問題研究

殷凱琳,歐志英

(蘭州理工大學理學院,蘭州 730050)

0 引言

粘彈性梁理論對土木工程及阻尼技術具有重要的指導意義。粘彈性材料是在外力作用下,彈性與黏性兩種變形機制同時存在的材料。材料的粘彈性性質依賴于時間、溫度、負荷、加載速率及應變幅值等條件。許多固態(tài)新物質、新材料的力學特性超出了彈性范疇,使得粘彈性理論的出現與發(fā)展成為必然。粘彈性材料憑借彈性、黏性及減震等特性已逐漸應用于工程及航空航天領域。在載荷及環(huán)境影響下,其表現出隨時間變化的粘彈性響應。常保平[1]在線性粘彈性范圍內研究了粘彈性梁的動力特性。張建文等[2]考慮了具有介質阻尼及非線性粘彈性本構關系的梁方程,由此得到在一定的條件下所給偏微分方程等價于—常微分方程組的初值問題。Chen等[3]研究了以軸向脈沖速度運動的粘彈性光束橫向振動的主要參數共振及粘彈性軸向運動梁的非線性動力學行為。艾智勇等[4]采用分數階Merchant模型研究飽和地基的流變固結,并在此基礎上探討分數階次與地基成層性對梁與粘彈性飽和地基共同作用的影響。

本研究著重將粘性系數引入分數階微分方程的階數,基于Euler-Bernoulli梁理論建立了粘彈性梁在位移應變條件下的分數階動力學模型。相比整數階模型,分數階動力學方程的運用范圍更廣。采用同倫攝動法求解分數階微分方程,通過數值結果分析了材料粘性系數、阻尼比及固有頻率對梁模型振動的影響。

1 基礎知識

近年來,分數階微分方程(FDE)已被廣泛研究并應用于諸多學科(如物理、化學、數學、工程等),其中最常見的是以下兩種形式:Riemann-Liouville型定義采用微分-積分形式避免了極限求解。在粘彈性材料研究中引入Caputo型微分,現實實際問題建模過程中廣泛應用Caputo型定義。

定義1:Riemann-Liouville型[5]

(1)

性質1:線性性質

(2)

此性質可通過簡單的代數運算證明,并對所有其他類型的定義也成立。

性質2:由定義

(3)

交換積分次序得

(4)

定義2:Caputo型

(5)

其性質類似Riemann-Liouville型。

2 問題模型

梁理論是一個簡化線性彈性理論,用于計算梁受力與變形特征,是梁得以運用于工程力學、經典梁力學的基石。梁理論基本建立了有關經典梁模型的全套理論體系,是后續(xù)一切梁分析的核心。結合梁理論考慮如圖1所示的粘彈性梁模型,具有均勻軸向運動、密度ρ、截面積A、慣性矩I及初始張力P0的粘彈性梁在外部激勵F(x,t)的作用下沿棱以軸向傳輸速度v(t)移動,棱的兩端相隔距離L。僅考慮橫向位移u(x,t)描述的彎曲振動,其中t是時間坐標,x是軸向坐標。

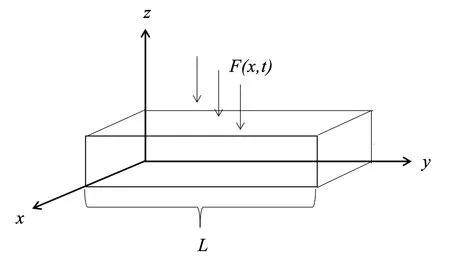
圖1 軸向運動的粘彈性梁模型Fig.1 Viscoelastic beam model with axial motion

Euler-Bernoulli梁方程是一個關于工程力學、經典梁力學的重要方程,其內容描述了梁的位移與載荷的關系:

(6)

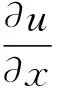
通過分析梁的動力學方程、牛頓第二定律及歐拉-伯努利假設,忽略慣性矩與剪切變形,可以得到梁的動力學控制方程。結合本構方程、動力學方程及邊界條件的無量綱變換,對非線性動力學模型進行簡化。假設粘彈性材料服從分數開爾文-沃特模型,故材料的本構方程[6]可以寫成:

(7)

其中,φ(x,z,t)是法向應力,ω(x,z,t)是軸向應變,E0(x)是梁材料的楊氏模量,E1(x)是剪切模量,α是黏度系數。

在固體力學中,彎曲力矩是指當外力或力矩施加到結構元件上時,在結構元件中引起的反作用力導致元件彎曲。為了平衡,外力或外力產生的力矩必須由內部荷載引起耦合平衡,其中產生的內部耦合稱為彎矩,因此彎矩是當外力或力矩施加到元件上時在結構元件中引起的反應,也是對應施加外力合成的內力偶分量。任何截面上的彎矩-應力關系由以下公式確定:

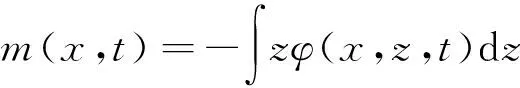
(8)

根據牛頓第二定律和歐拉-伯努利假設,忽略慣性矩與剪切變形,得到梁的動力學控制方程:

(9)

3 定解問題的求解

對于無限制的小變形效應,可以將位移關系表示為:

(10)

梁的彎矩:

(11)

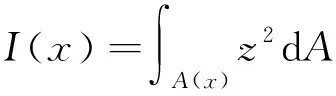
(12)

這里參數ρ、A、v、E0、I、E1、P0、φ是常量。

近年來,同倫攝動法(HPM)被廣泛應用于求解分數階微分振動、異常擴散、非線性波動、阻尼控制等問題,其主要思想是根據已知方程構造同倫函數。以下面的方程式為例:

L(u)+N(u)=f(r),r∈Ω

(13)

其中,L是線性算子,N是非線性算子,f是已知的解析函數,Ω為r所符范圍。建立以下同倫格式:

H(v,p)=(1-p)[L(v)-L(u0)]+p[L(v)+N(v)-f(r)]=0

(14)

或簡化為:

H(v,p)=L(v)-L(u0)+pL(u0)+p[N(v)-f(r)]=0

(15)

其中,p∈[0,1]中的是一個隱含參數。假設上述方程的解具有以下形式:

v=v0+pv1+p2v2+…

(16)

當p接近1時,可獲得以下結果:

(17)

這是原方程的解。

將同倫攝動方法應用于非線性問題[7],可獲得解析近似解。本研究使用一種新的改進同倫攝動方法[8]來解決問題。將方程式(12)改寫為:

(18)

構造同倫函數:

(19)

根據該方程在相應載荷條件下的解,用數值結果說明基于USD控制方程粘彈性梁的響應。此處考慮簡支梁,f(x)表示為:

(20)

可將其看作是單自由度理想梁的力分布,通過截斷無限階來進行數值計算。參考文獻[9]中的模型,假定在USD控制方程中E1/m=2ηw3/2、w2=E0I/ρA。

這里ρA=1、L=π、m=1、v=0.2、P0=0.6、φA=0.8,其中η是阻尼比,w是固有頻率。

設定條件中固有頻率w=5 rad/s,阻尼比η=0.5與α=0.5,繪制梁的橫向運動如圖2所示。

圖2 USD控制方程的單位階躍響應Fig.2 Unit step response of USD control equation

結果表明,粘彈性梁在初始時刻先開始振蕩,逐漸趨于靜態(tài)平衡位置。為了比較不同分數階α對梁振動的影響,分析了局部階躍響應。

為了進一步驗證分數階α對USD模型中粘彈性梁振動的影響,取參數α=0.4、0.5、0.6、0.7,繪制u(x,t)隨x與t變化的圖像。

圖3顯示,當時間坐標固定,粘彈性梁沿軸向坐標的振動隨著α的增加而減小。當軸向坐標固定,粘彈性梁沿時間坐標的振動隨著時間增加慢慢趨于靜態(tài)平衡狀態(tài),且α越小,其接近平衡的速度越快。在USD控制方程中固定分數階的條件下,分析阻尼比與固有頻率對軸向運動粘彈性梁振動的影響,展示當阻尼比不同時,粘彈性梁在USD模型下的振動變化。

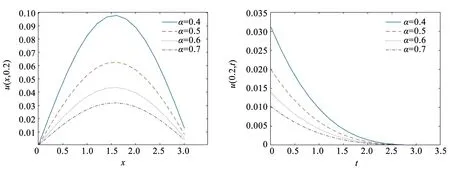
圖3 USD-α對梁振動的影響Fig.3 Influence of USD-α on beam vibration

圖4顯示,當時間坐標固定,阻尼比越小,粘彈性梁的振動越大。當軸向坐標固定,阻尼比越小,梁的振動趨于平衡靜態(tài)位置的速度越快。以下展示當固有頻率w取不同值時,粘彈性梁在USD模型下的振動變化。

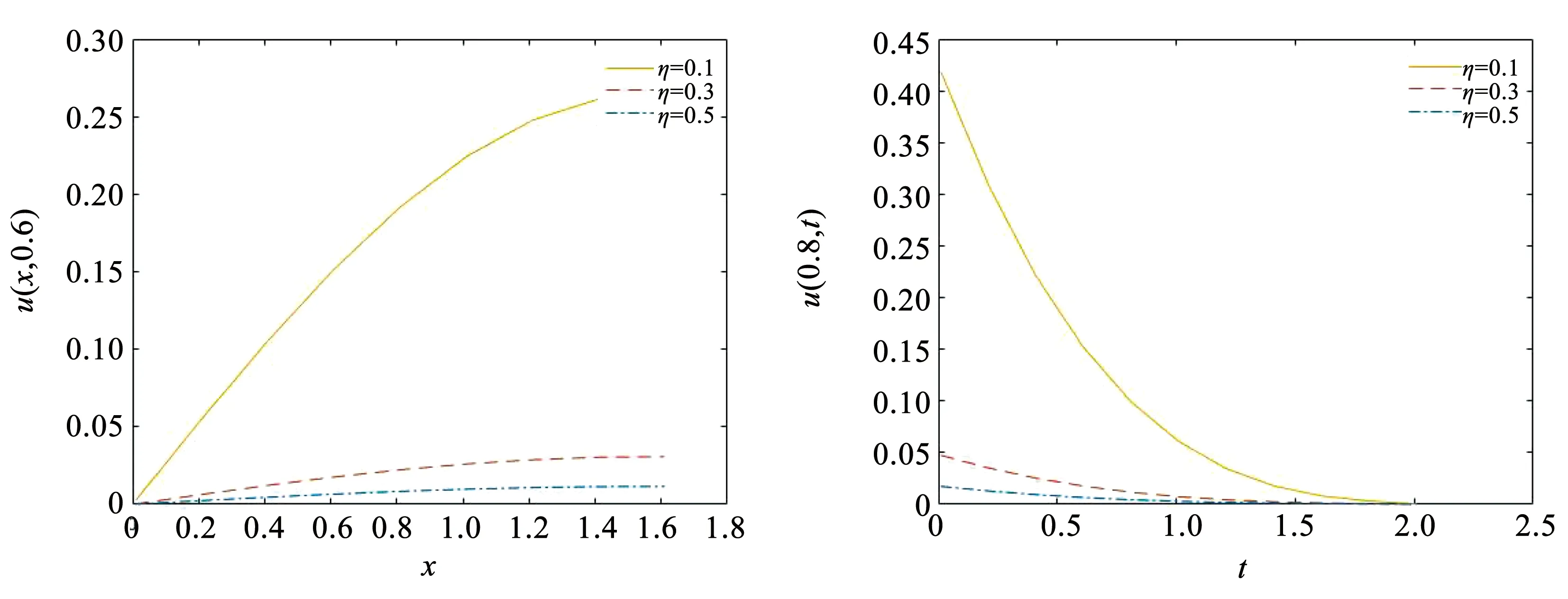
圖4 USD-η對梁振動的影響Fig.4 Influence of USD-η on beam vibration

圖5顯示,當時間坐標固定,固有頻率越大,粘彈性梁隨軸向坐標變化的振動越大。當軸向坐標固定,在x=1.4前,固有頻率越高,梁的振動越快趨于平衡靜態(tài)位置。在x=1.4后,固有頻率越低,梁的振動越快趨于平衡靜態(tài)位置。根據算例分析可得到USD模型中梁振動隨各參量的變化,如表1所示。

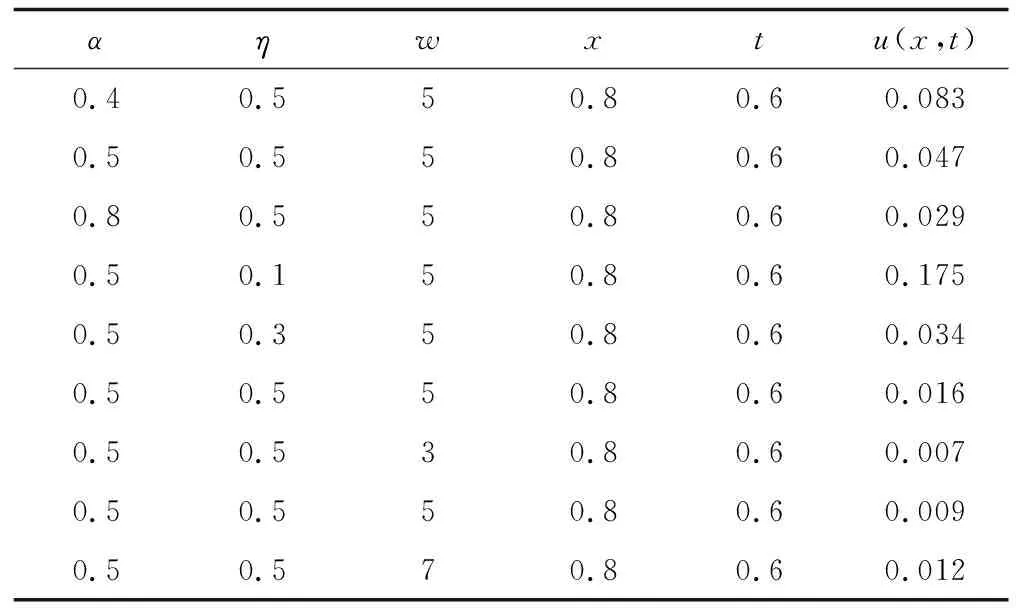
表1 各參數與USD模型的關系Tab.1 Relationship between various parameters and the USD model

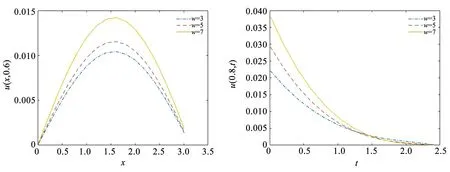
圖5 USD-w對梁振動的影響Fig.5 Influence of USD-w on beam vibration

對于階躍響應函數的作用,軸向運動的粘彈性梁經歷了非常不同的過程,先在靜態(tài)平衡位置附近振蕩,緩慢地趨于零位移。也可以相應地對脈沖響應函數進行分析,通過改變系數值來總結結果與變量之間的關系。

4 結論

基于Euler-Bernoulli梁理論建立了分數階型USD粘彈性梁模型,通過數值模擬對其響應進行分析。結果表明,分數階、阻尼比及固有頻率對梁的橫向位移的振動有不同的影響。改進同倫攝動法可用來求解具有任意階數的分數微分的線性微分方程,其可以描述分數階粘彈性梁的結構,從而得到簡支梁在受階躍與脈沖兩種負載情況下的無窮求和表達式的解。從數值結果比較可得出分數階變化對USD模型影響最大,阻尼比變化及固定頻率變化對模型影響較小。本研究考慮的應用模型是粘彈性梁,其方法也可參考適用于其他類型的梁模型系統(tǒng)。