北斗系統橋梁變形監測和預警研究

郝 龍,邵 慧,姜 丹

（中交第一公路勘察設計研究院有限公司,陜西 西安 710065）

0 引言

近二十年來，隨著我國經濟和交通的發展，建設的橋梁數量越來越多，截至目前已達到約100萬座。橋梁在各種外荷載和自身作用下會發生變形，這種現象對于特大型橋梁尤為明顯[1]。特大型橋梁在風荷載作用下會產生風－車－橋耦合共振，如廣東虎門大橋豎向彎曲振動，這種振動會引起橋梁發生較大的變形，變形超過允許值后極易發生橋梁安全事故。因此，對特大型橋梁開展健康監測并建立安全預警系統極為重要[2-3]。

隨著北斗技術的發展，其高精度自動化監測系統已經在橋梁結構中開始應用。包龍生等[4]對北斗系統的周跳現象進行了分析，在傳統算法的基礎上，提出一種改進的Turbo Edit算法，可以明顯提高北斗系統測量的精度，滿足高精度變形監測。余加勇等[5]對全球導航衛星系統的橋梁健康監測方法研究進展進行了綜述，詳細介紹了GNSS在橋梁健康監測中的研究現狀、熱點方向、發展機遇和挑戰，最后指出了各種導航系統橋梁健康監測面臨的關鍵問題。楊長風等[6]對北斗系統的國際化發展進行了研究，分析了北斗系統應用國際化的優勢、機遇和挑戰，明確了北斗系統的發展目標。靳明等[7]以鄭州黃河大橋為工程背景，建立了橋梁健康監測系統并對其進行了預警設計，實時監測橋梁結構在運營階段的安全狀況。

橋梁健康監測系統對數據進行采集和保存后，應根據收集到的數據對橋梁的損傷和安全狀況進行評估，建立預警機制，以確保橋梁安全地運營[8]。該文首先介紹了北斗衛星系統的組成和橋梁變形監測算法，然后建立了橋梁結構安全預警系統，以期對橋梁健康監測提供參考。

1 北斗橋梁變形監測

1.1 變形監測系統組成

基于北斗高精度技術的橋梁監測系統由數據傳輸子系統、基準站、監測站和變形監測平臺幾部分組成。北斗橋梁變形監測原理如圖1所示。

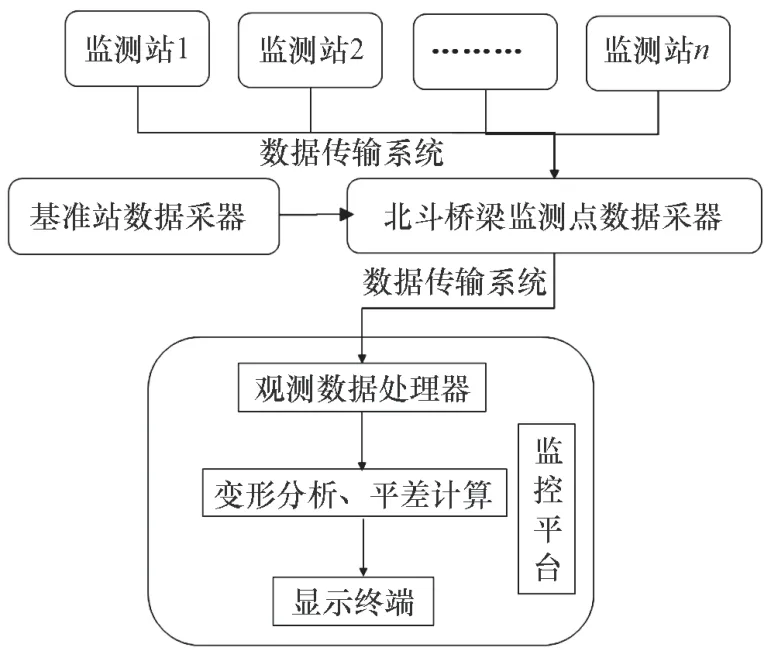
圖1 北斗橋梁變形監測原理示意圖

基準站的作用為接收北斗衛星傳來的信號，并將接收到的數據和自身坐標經過修正后通過數據傳輸系統傳遞給監測站。監測站的作用為同時接收北斗衛星和基準站傳來的信息，然后將采集到的兩者之間的信息進行相對差分處理，得到監測站相對于基準站的變形數據，并將該數據傳輸給變形監測平臺。變形監測平臺的作用為接收各個監測站傳來的數據，然后通過北斗解算軟件對數據進行處理，橋梁的變形狀態通過圖、表等方式直觀地顯示出來，進行實時監測供用戶查看。

1.2 監測算法

載波相位法是北斗衛星系統采用的常見高精度定位方法。采用該方法進行定位時，需要快速精確地確定其整周模糊度。假設地面接收器a和b同時接收衛星1和2傳遞來的信號，則載波相位的數量計算公式如下：

式中，φ——使用載波相位的數量；λ——衛星信號的波長；r——北斗衛星與接收器之間的距離；N——載波相位整數的模糊度；ε——接收器接收載波相位信號時的測量噪聲。

通常衛星到地面接收器之間的信號傳播可視為平行傳播，g可表示為基準站到衛星之間的方向向量，h可表示為基準站到監測站之間的方向向量，則基準站和監測站到衛星1的距離計算公式如下：

式中，h的值為[δx,δy,δz]T；g1的值為

同樣，基準站和監測站到衛星2的距離計算公式如下：

式中，h的值為[δx,δy,δz]T；g2的值為

將式（2）和（3）代入式（1）可得：

在時間t時，基準站和監測站同時測得衛星數量為n+1時，在觀測結果中有n個雙差觀測值，將其中一個作為參考值，則有n組載波相位方程，其公式如下：

式中，Pt——t時間時載波相位向量組；At——k×3階系數矩陣；h——基準站與監測站之間的方向向量；N——整周模糊度的n維向量；εt——噪聲誤差組成的n維向量。

基準站和監測站連續觀測m個周期時，由式（4）和（5）可推出通用方程：

式中，P——觀測值的mn×1維向量；A——位置系數的mn×3維向量；B——整周模糊度的mn×n維向量；ε——噪聲誤差組成的mn×1維向量。

北斗系統整周模糊度使用初始解和測量方程得到的誤差來確定其實際范圍，其計算公式如下：

進行高精度定位時，需解算基準站和監測站之間的方向向量h和模糊度的整周數N，使用最小二乘法對式（7）進行求解，得到最小目標函數：

式中，R3——三維空間矩陣；Zn——n為整數空間矩陣。

式（8）為求解含有整數參數的約束問題，應用最小二乘法求最優解，式（8）可分解如下：

應用最小二乘法求解h和N時，首先忽略N為整數的約束條件，求得N的范圍，則式（6）可以計為下式：

結合式（8），可以求出基準站與監測站之間的方向向量h，其計算公式如下：

將求得的h代入式（9）可得：

由式（11）和式（12）分別求得的h和N值為模糊度的浮點解。該解與協方差矩陣之間的關系如下式：

在整周模糊度參數已經求解出的前提下，式（13）的值比式（11）的值會更加精確。應用上式求得整周模糊度的范圍和協方差矩陣后，使用最小二乘法重復求解方程，得出所有解的最小值即可得到載波相位的整周模糊度N，目標函數方程計算公式如下：

該公式可記為下式：

使用北斗衛星系統進行實時監測時，由于各種外在因素影響，很難達到理想條件，即協方差矩陣不一定為對角矩陣，此時應用最小二乘法求解就會降低速度。LAMBDA算法應用最小二乘法的平差法使用浮點解求出最小的模糊度按照N1到Nn的順序求解最小值，由于整周模糊度的相互關聯性，求出N1到Ni-1的值后即可得到Ni的值的限定范圍，從而求解出Nn。因此應用LAMBDA算法比最小二乘法更有優勢。

在已知X值后求解Y值，則估值的平均值如下式所示：

式中，mY——最小二乘估計Y的平均值；σYX——Y和X的協方差。

根據式（17），整周模糊度的目標函數如下：

2 北斗橋梁變形監測預警系統

北斗高精度自動化橋梁變形監測系統應對監測數據做出快速化響應，超限時能夠及時預警，使得大型橋梁結構的運營安全能夠得到保障。預警系統包括預警指標、預警閾值和預警流程三個方面，其中預警指標的建立應依靠監測系統的實時監測數據，預警閾值可以依據國家規范、理論公式和區域數據統計建立，最后根據預警指標與預警閾值比對結果設定相應的預警流程。

2.1 預警指標

大型橋梁結構的預警系統應選用對橋梁結構安全有重要影響的指標作為其預警指標，該類指標可以通過北斗橋梁監測系統實時獲取。大型橋梁預警指標主要有主梁撓度變形、主梁水平變形、橋塔變形、固有頻率變化和纜索變形等。

主梁撓度變形作為橋梁線形方面的預警指標，其數值可以通過布設在主梁跨中、1/4截面和3/4截面的監測點獲取。主梁水平變形分為縱向位移和橫向位移，縱向位移會影響伸縮縫和梁端阻尼器的工作狀態、橫向變形會影響支座的工作狀態，該類指標可以通過布置在梁端的監測點獲取。橋塔變形主要有水平位移、塔體傾斜等，該類型的變形可通過布設在橋梁主塔頂部的監測點獲取。橋梁的固有頻率變化可作為全橋整體振動特性方面的預警指標，其值可以通過橋梁振動監測數據獲取。纜索變形包括主纜和斜拉索的變形，纜索變形可作為橋梁整體受力方面的預警指標，其值可以通過布設在纜索上的監測點獲取。

2.2 預警閾值

預警閾值的設置關系到監測系統能否及時發現結構受力異常并發出預警信號。預警系統設置三級預警，各級預警閾值Δ1m、Δ2m和Δ3m用戶根據橋梁各結構在不利荷載作用下的響應值進行設置，通過實時監測值Δ0與預警閾值Δm進行對比劃分出預警等級。

2.2.1 正常狀態（綠色）

正常狀態下，監測值與預警閾值之間應滿足以下關系：

正常狀態下，監測值均小于一級預警閾值，橋梁結構處于安全運營狀況，無安全隱患。

2.2.2 一級預警（黃色）

一級預警狀態下，監測值與預警閾值之間應滿足以下關系：

一級預警狀態下，北斗技術橋梁監測系統發現影響橋梁結構安全運行的隱患，變形值異于正常值，系統會自動增加監測頻率，同時，做出黃色預警并通過各種方式反饋給用戶。

2.2.3 二級預警（橙色）

二級預警狀態下，監測值與預警閾值之間應滿足以下關系：

二級預警狀態下，北斗技術橋梁監測系統發現某項或某幾項值超過二級預警閾值，影響結構安全，系統做出橙色預警反饋給用戶。用戶應對結構構件進行檢查和受力分析。

2.2.4 三級預警（紅色）

三級預警狀態下，監測值與預警閾值之間應滿足以下關系：

三級預警狀態下，北斗技術橋梁監測系統發現某項或某幾項值超過三級預警閾值，發現嚴重危及橋梁結構的異常荷載，用戶需對橋梁結構進行全方面評估。

2.3 預警流程

大型橋梁結構是一個復雜的系統，眾多的預警指標如果不加以處理，直接用監測值去評價橋梁的健康狀態是很難的。因此應采用綜合指標預警策略作為橋梁結構的預警方式。利用層次分析法可以對多個預警指標進行權重分配，然后對各層指標進行評分。預警流程如圖2所示。

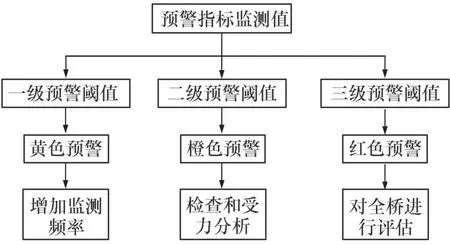
圖2 三級預警流程

3 結語

基于北斗高精度自動化監測系統已經在橋梁結構中應用并有了新的發展，但是該技術在實際應用時受到諸多因素的影響，使其功能并不能很好地發揮出來，因此需要不斷地進行研究，以提高其監測水平。該文介紹了北斗衛星系統組成、監測算法和預警系統，以期為北斗高精度技術的大型橋梁健康監測提供借鑒。