基于權系數法的功率和載荷協同控制策略

張良,何山,2*

(1.新疆大學電氣工程學院,烏魯木齊 830047; 2.可再生能源發電與并網控制教育部工程研究中心,烏魯木齊 830047)

隨著風輪直徑的不斷增大,風輪不平衡載荷引起的風機折損失效成為風電機組運維成本的重要來源[1-2],因此,利用獨立變槳技術在穩定因風速的湍流特性、風切變和塔影效應引起的輸出功率波動的同時減小不平衡載荷,延長風機使用壽命成為當今風力發電技術的主要突破口[3]。

目前,國內外對獨立變槳控制策略已有一些研究。文獻[4]為抑制不平衡載荷,建立風機運動數學模型,提出一種基于模型預測控制(model predictive control,MPC)的獨立變槳控制策略。文獻[5-6]分別將反饋神經網絡(back propagation,BP)和徑向基函數(radial basis functions,RBF)神經網絡和與比例、積分和微分(proportional integral derivative,PID)控制器相結合,優化PI參數,在穩定輸出功率減小變槳頻率的同時對降低俯仰載荷和偏航載荷也有顯著效果。文獻[7-8]在卡爾曼坐標變換的基礎上提出線性二次高斯函數(linear quadratic regulator,LQG)控制器實現了載荷的最優控制。文獻[9]采用模糊PID提高風機變槳系統的抗干擾能力,穩定了輸出功率。文獻[10]在統一變槳控制的基礎上將頭腦風暴算法優化的PID控制器與根據槳葉方位角反饋的權系數獨立變槳控制相結合,在穩定功率的同時一定程度上降低了不平衡載荷。文獻[11]在統一變槳的基礎上將輸出功率三倍頻信號疊加到權系數上顯著減小了功率波動。文獻[12]將支持向量機與權系數分配的獨立變槳相結合,在穩定功率的同時一定程度上降低不平衡載荷。文獻[13]在權系數獨立變槳的基礎上引入自適應控制,在穩定輸出功率從的同時一定程度上緩解了不平衡載荷。上述研究方法雖各具特點,但總體分為兩種控制路線:一類是以槳葉載荷作為反饋設計獨立變槳控制器,該方法雖在一定程度上穩定輸出功率,但其主要目的是降低風輪面上的不平衡載荷,以期延長風機使用壽命;另一類以輸出功率或者風輪轉速作為反饋設計統一變槳距控制器,再以槳葉不同方位角設計權系數并進行獨立變槳,由于設計權系數時槳葉上的風速采用的是等效風速,且不平衡載荷處受風切變和塔影效應影響外還收其他因素影響。因此,權系數法相較于降低不平衡載荷,其在穩定功率方面更顯著。總之,上述控制路線均存在側重,未能考慮在穩定功率的同時降低不平衡載荷。

聚焦于穩定輸出功率和抑制不平衡載荷兩個方面,結合方位角反饋和載荷反饋的優點,提出一種基于權系數法的功率和載荷協同控制的獨立變槳協同控制策略。為穩定功率,采用遺傳算法優化的PID(genetic algorithm optimized PID controller,GA-PID)作為主控制器,并以風輪實時轉速與額定轉速的偏差作為控制器的輸入;在載荷控制方面,根據方位角反饋得到各槳葉的動態權系數,并在此基礎上設計載荷反饋模糊PID控制器,得到各槳葉載荷影響下的槳距角微調量。通過MATLAB/Simulink和FAST進行聯合仿真,驗證了該方案在穩定功率和抑制不平衡載荷方面均具有顯著效果。

1 風機理論模型

1.1 風機功率捕獲原理

根據貝茲(Betz)理論,氣流通過風輪掃掠面流速降低形成壓降,從而使風輪獲得動能,推動風輪轉動。其具體捕獲動能的計算公式為

(1)

式(1)中:s為風輪掃掠面積;ρ為空氣密度;v為通過風輪面的氣體流速;β為槳距角;λ為葉尖速比,λ=ωR/v,其中w為葉素處相對風速,R為槳葉長度;CP為風機葉輪的風能捕獲系數,而在高風速區域,其表達式為

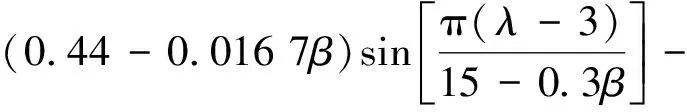
0.001 84(λ-3)β

(2)

則風能捕獲系數CP隨槳距角變化如圖1所示,通過式(1)和圖1可知,控制槳距角即可改變風輪的能量捕獲系數,從而實現穩定功率的目的。

圖1 風能捕獲系數特性曲線

1.2 葉根氣動載荷分析

對風機槳葉進行氣動載荷分析通常采用葉素理論。以距離葉根r處的葉素為例,其氣流速度三角形和受力如圖2所示。

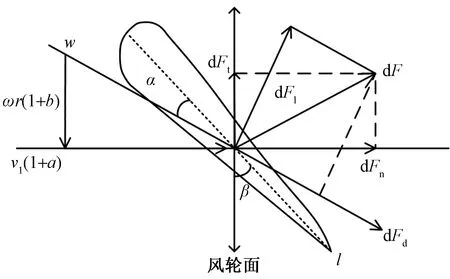
α為葉素攻角;β為槳距角;ω為槳葉轉動角速度;v1為來流風速;a和b分別為軸向誘導因子和切向誘導因子;l為距離葉根處r的槳葉剖面弦長;dF為合成風速w在葉素處產生的力,其既能分解葉素處的法向力dFn和切向力dFt,又能分解為葉素處的升力dFl和阻力dFd

槳葉葉根處的擺振力矩Mx和揮舞力矩My計算公式分別為

(3)

(4)

式中:r0為輪轂半徑;R為槳葉長度;w和φ分別為葉素處相對風速和入流角;Cl和Cd分別為葉素處對應攻角的升力系數和阻力系數。

由葉素理論可知葉根彎矩的大小取決于入流角,而入流角φ=α+β,因此通過調節槳距角β即可調節入流角的大小,從而能實現對葉根彎矩進行控制。

2 協同變槳控制原理

以穩定輸出功率、抑制槳葉揮舞力矩和降低風輪不平衡載荷為目的,結合權系數獨立變槳和載荷反饋獨立變槳的優點,提出基于權系數法的功率和載荷協同控制策略,以遺傳算法優化的PID作為主控制器,以方位角反饋的權系數法穩定輸出功率的同時初步抑制風輪不平衡載荷,在此基礎上增加載荷反饋的模糊PID控制環節對槳距角修正,以此抑制載荷。其控制框圖如圖3所示。

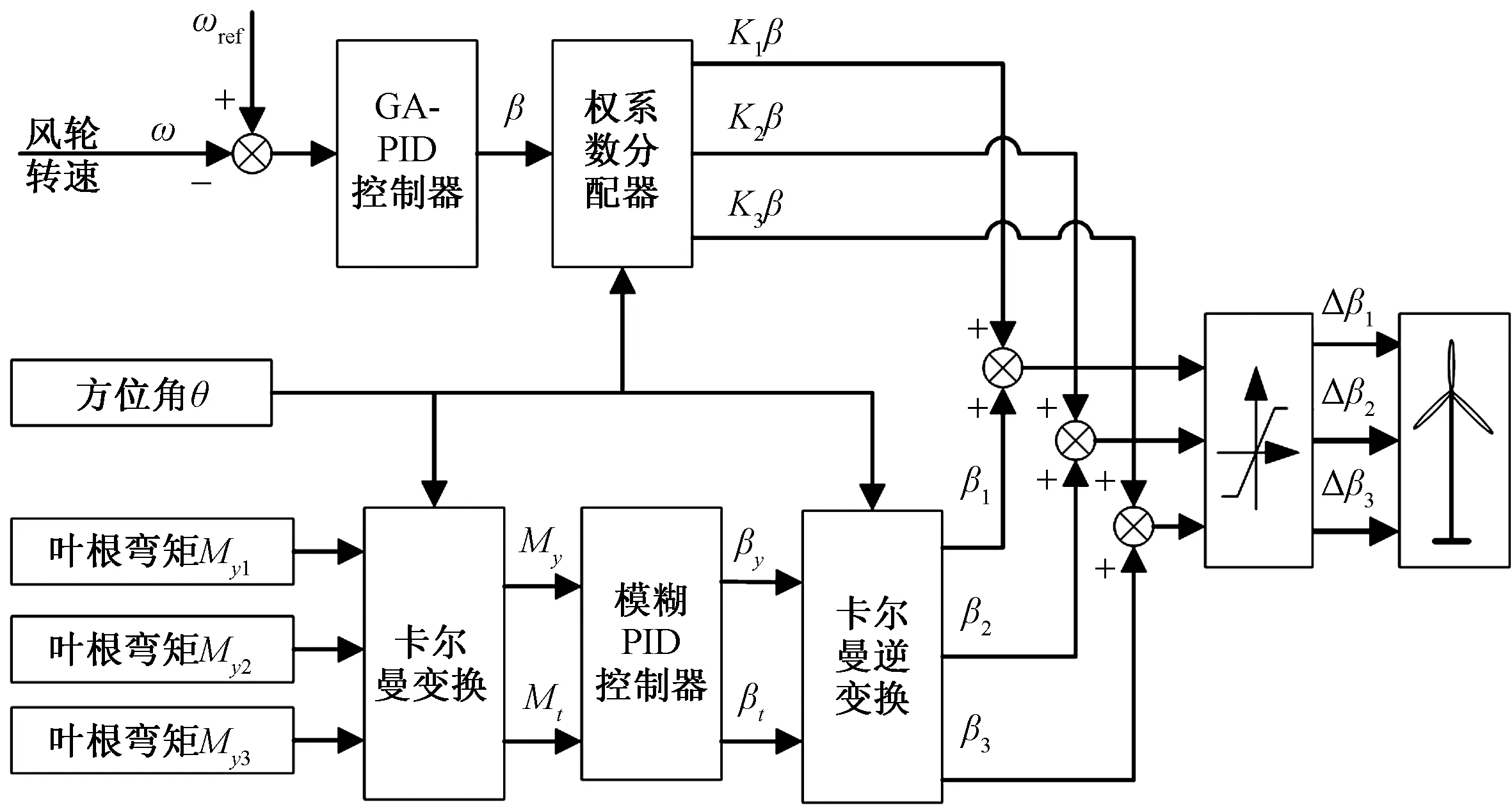
圖3 功率和載荷協同控制框圖

首先,將風輪轉速與額定轉速的偏差作為主控制器的輸入,從而得到三支槳葉的統一變槳距信號β;其次,由方位角反饋得到各槳葉的動態權系數Ki(i=1,2,3),并由分配器重新分配各槳葉的槳距角Kiβ;最后,在此基礎上再由載荷反饋通過模糊PID控制器得到載荷影響下的各槳葉微調量βi,從而完成協同獨立變槳控制。每只槳葉槳距角變化量計算公式為

(5)

2.1 方位角權系數分配模型

規定以過風輪面中心的水平線為起始位置,槳葉逆時針旋轉方向為正方向,槳葉軸線與水平線的夾角為方位角θ,選定任一槳葉為基準,命名為槳葉1,則槳葉2和槳葉3的位置分別為θ+120°和θ+240°。在風剪切效應影響下,假定風機各槳葉所受平均風速等效為整支槳葉1/2位置處風速,則其等效風速計算公式為

(6)

式(6)中:R為槳葉長度;H0和V0分別為輪轂中心高度及其中心高度處風速;θ為第i支槳葉的方位角;Vi(i=1,2,3)為各槳葉所受等效風速;n為風切系數。

在風機參數確定及空氣密度不變的情況下,槳葉軸向氣動力與風速平方成正比[14],則在高風速區隨槳葉方位角變化,受風切效應影響下的各槳葉的權系數Ki(i=1,2,3)計算公式為

(7)

2.2 主控制器設計

為穩定輸出功率,以風輪轉速ω和期望轉速ωref的誤差e(t)作為主控制器的輸入,則控制量u為

(8)

e(t)=ω-ωref

(9)

由式(8)可知,只需整定出合適的KP、KI和KD,即可達到理想的控制效果。而傳統的PID控制器的參數整定不僅需要豐富的經驗,且操作過程煩瑣,最主要的是,控制對象一旦發生變化,控制參數就需重新整定,不具有適應性。遺傳算法因其整體搜索策略和優化方法不依賴于梯度信息和其他輔助知識,只需要影響搜索方向的目標函數和合適的適應度函數,不依賴于問題的具體領域,提供了一種解決復雜問題的通用框架,且由于其流程簡單,在許多領域:諸如參數整定、目標尋優、路徑規劃等得到廣泛應用[14-15]。因此,為解決上述問題,引入遺傳算法對PID控制器各參數進行優化整定,其流程如下。

(1)參數初始化:設定種群數規模M=50,進化代數G=100,PID控制器各參數范圍KP∈[1,15]、KI∈[1×10-3,7]、KD∈[1×10-3,2]

(2)確定適應度函數:當超調量ey(t)>0時,且ey(t)=y(t)-y(t-1),以上升時間、累計絕對誤差和控制輸入作為優化指標,則目標函數為

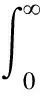
(10)

式(10)中:e(t)為系統誤差;u(t)為控制器輸出;tu為上升時間;w1、w2和w3分別為對應權重。

當超調量ey(t)<0,引入懲罰機制,即系統超調時將超調量作為最優指標項之一,此時目標函數為

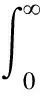
(11)

式(11)中:y(t)為被控對象的輸出,且w4?max(w1,w2,w3)。

定義遺傳算法適應度函數為F=1/J,其中w1=0.9,w2=0.03,w3=0.7,w4=20。

(3)選擇、交叉和變異。

(4)重復步驟三,直至滿足算法要求。

則遺傳算法優化PID流程如圖4所示。

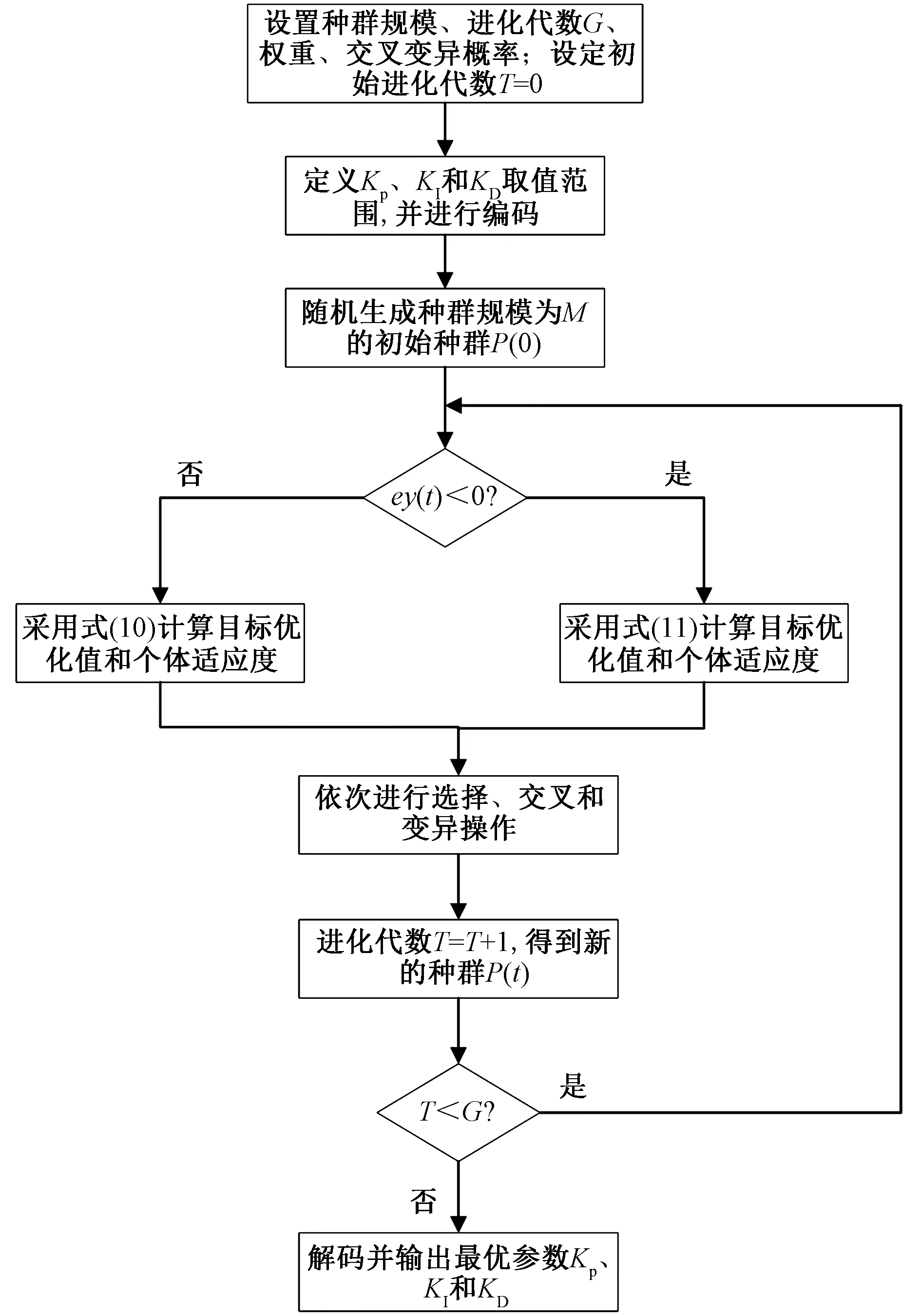
圖4 GA-PID 算法流程圖

2.3 載荷反饋控制器設計

旋轉坐標系下槳葉所受的揮舞力矩Myi(i=1,2,3)是一個周期變化量,無法采用傳統的線性控制理論設計載荷控制器,因此,利用卡爾曼坐標變換,將旋轉坐標系下的揮舞力矩Myi轉換至靜止坐標系下的輪轂俯仰力矩Mt和偏航力矩My[16],其轉換公式為

(12)

式(12)中:θ1、θ2和θ3分別為各槳葉的方位角,且θ2=θ1+2π/3,θ3=θ1+4π/3。

在靜止坐標系下,便可用經典控制理論設計兩個載荷控制器,分別對俯仰力矩和偏航力矩進行控制,從而得到對應俯仰方向和偏航方向的期望槳距角βt和βy,再經過卡爾曼逆變換即可得到不平衡載荷影響下的各槳葉槳距角微調量,其變換公式為

(13)

由于傾覆力矩和偏航力矩波動幅度大、頻率高,無法用精確的數字描述,因此,在載荷控制方面使用模糊PID控制器。模糊控制能夠根據控制器的輸入實時對PID控制器的參數在線整定,具有一定的適應性,克服了傳統PID控制器適應性差的問題,使控制系統達到較好的控制性能,其結構如圖5所示,傾覆力矩和偏航力矩期望值均為0,將實際值和期望值作比較,即可得到模糊PID控制器的輸入:誤差e和誤差變化率ec,然后利用設置的模糊規則庫即可推理得到PID參數的實時在線整定值,將參數輸入PID控制器即能達到載荷的最佳控制。

圖5 模糊PID控制框圖

針對PID控制器的三個參數分別建立了三個模糊控制器,并定義控制器輸入量偏差e和偏差變化率ec的模糊子集為{NB,NM,NS,ZO,PS,PM,PB},并將其映射至論域[-4×103,4×103],定義模糊控制器的輸出KP、KI和KD模糊子集為{NB,NM,NS,ZO,PS,PM,PB},將其分別映射至論域[1.8×10-6,2.3×10-6]、[3×10-6,4×10-6]和[-1×10-10,1×10-10]。則控制器三個自適應參數KP、KI和KD的模糊規則如表1所示。

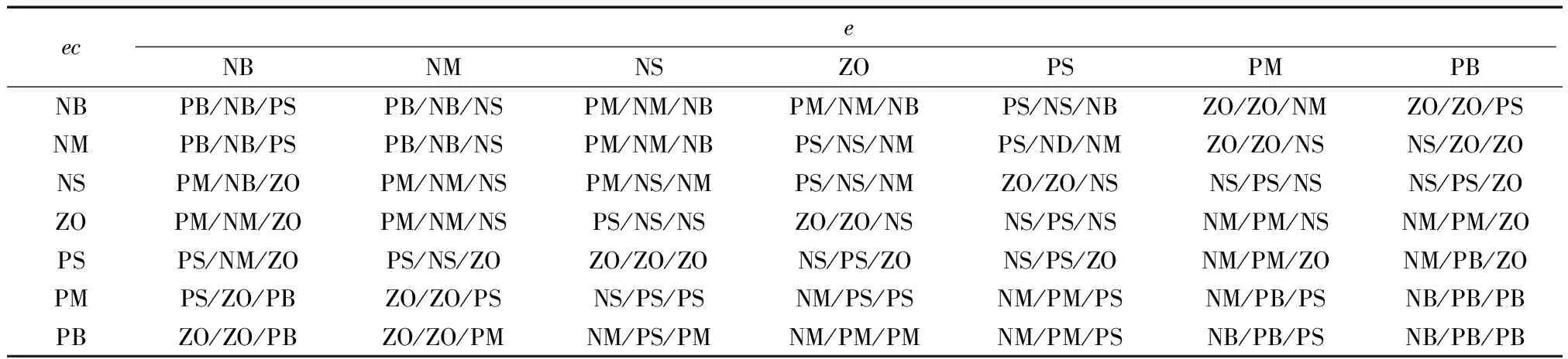
表1 KP,KI和KD控制規則表

根據上述各參數的控制規則表建立模糊規則庫,通過風機反饋回的葉根載荷,模糊控制器依據規則庫進行推理,從而得到參數KP、KI和KD,將得到的參數賦值給PID控制器即可實現對載荷的最優控制。參數KP、KI和KD隨載荷偏差和偏差變化率變化的整定如圖6所示。

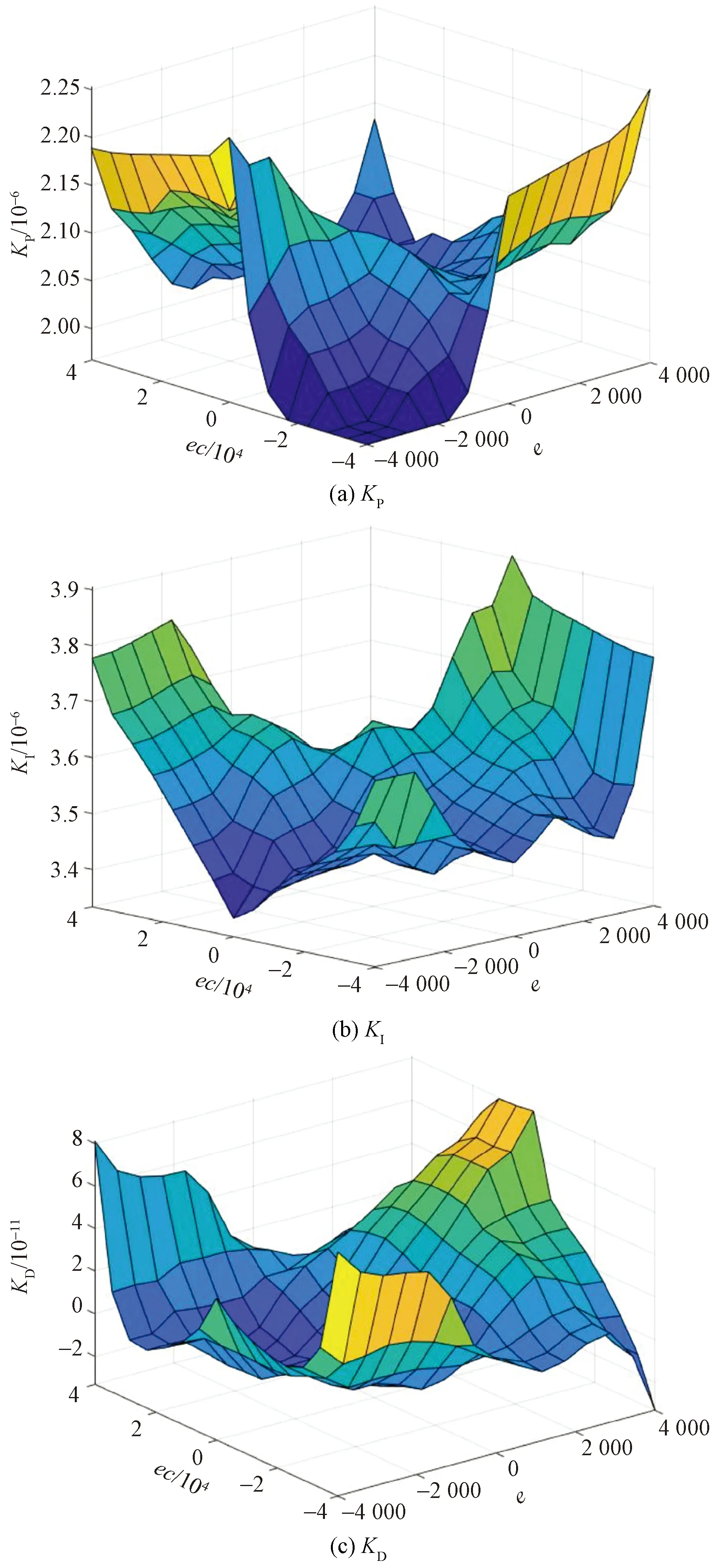
圖6 參數KP、KI、KD整定圖

3 仿真結果分析

3.1 仿真平臺和數據來源

為驗證功率和載荷協同控制策略的有效性,使用FAST軟件與MATLAB/simulink平臺進行聯合仿真,其聯合仿真模型如圖7所示。

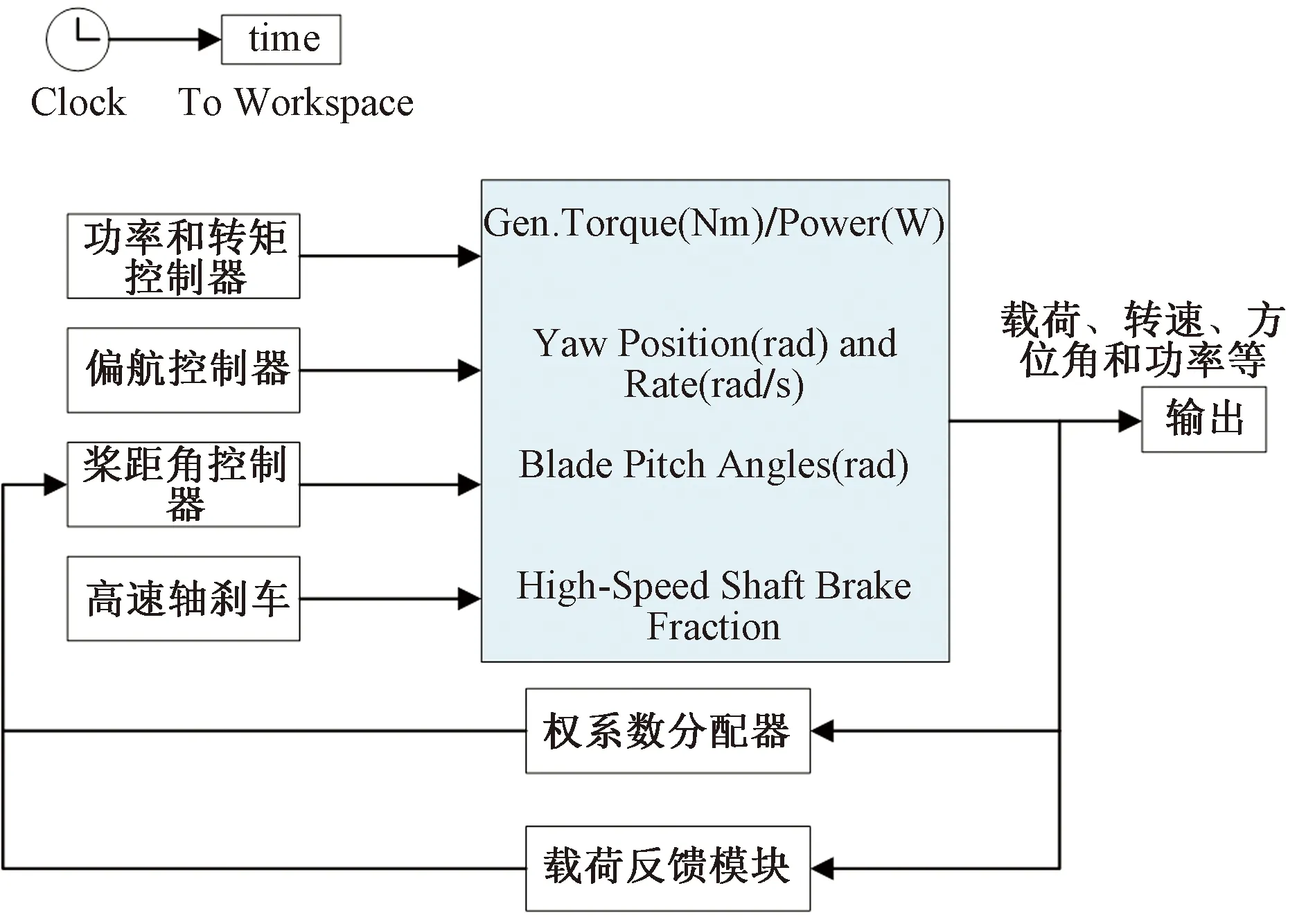
圖7 FAST-Simulink 聯合仿真模型

在聯合仿真模型中分別采用協同控制、統一變槳控制(collective pitch control,CPC)和獨立變槳(independent pitch control,IPC)PI控制(IPC-PI)對FAST非線性風機進行變槳控制,然后對仿真結果對比分析。采用NREL公司提供的5 MW陸基標準風機,其具體參數如表2所示。

表2 5 MW陸基風機具體參數

3.2 功率分析

為對比三種控制策略對于大型風機在高速風場中的控制性能,借助Turbsim依據IEC標準生成以輪轂高度為中心,平均風速為16 m/s,湍流強度為13%的湍流風,如圖8所示。在該風速下,風力發電機輸出功率如圖9所示,可以看出在相同風場,同一風速曲線作用下,風機狀態趨于穩定后,協同控制策略控制下,風機輸出功率相較于CPC控制和IPC-PI控制更穩定,特別是在60 s到80 s風速第一次劇烈突變時,CPC控制和IPC-PI控制下風機輸出功率皆存在較大的波動,而協同控制下風速突變對輸出功率的影響更小,能夠基本穩定在5 MW左右,總體控制效果更為理想,能夠很好地抑制高風速區的功率波動,具有較好的穩定性。

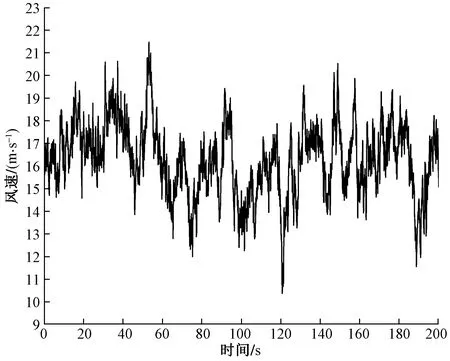
圖8 輪轂處風速變化曲線

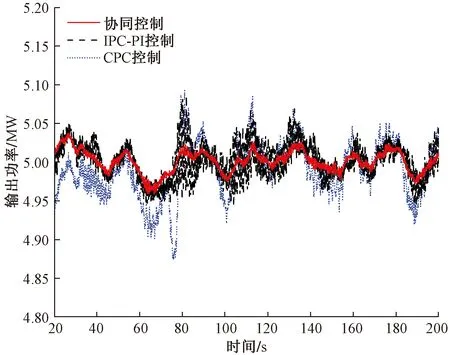
圖9 不同控制策略的風機輸出功率曲線

為驗證所提控制策略在不同風況下的有效性和適應性,借助IEC Wind生成如圖10所示,以輪轂中心風速為13.4 m/s,切變系數為0.2的階躍風。在該風況下風力機輸出功率如圖11所示,從整體來看,相較于CPC控制和IPC-PI控制,協同控制對于功率的穩定效果更好,在風速發生突變引起功率發生波動后,協同控制下的輸出功率波動幅度更小,且能以更快的響應速度將輸出功率穩定在額定功率附近。這說明了,在不同風況下,協同控制策略對于穩定輸出功率的效果更為理想。

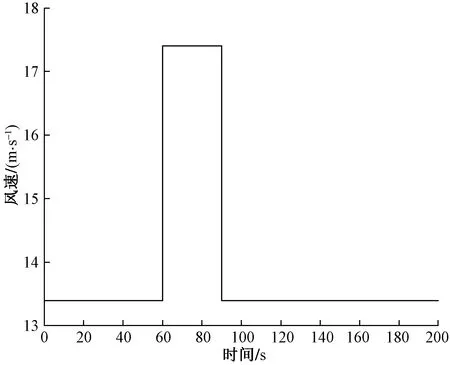
圖10 階躍風變化曲線

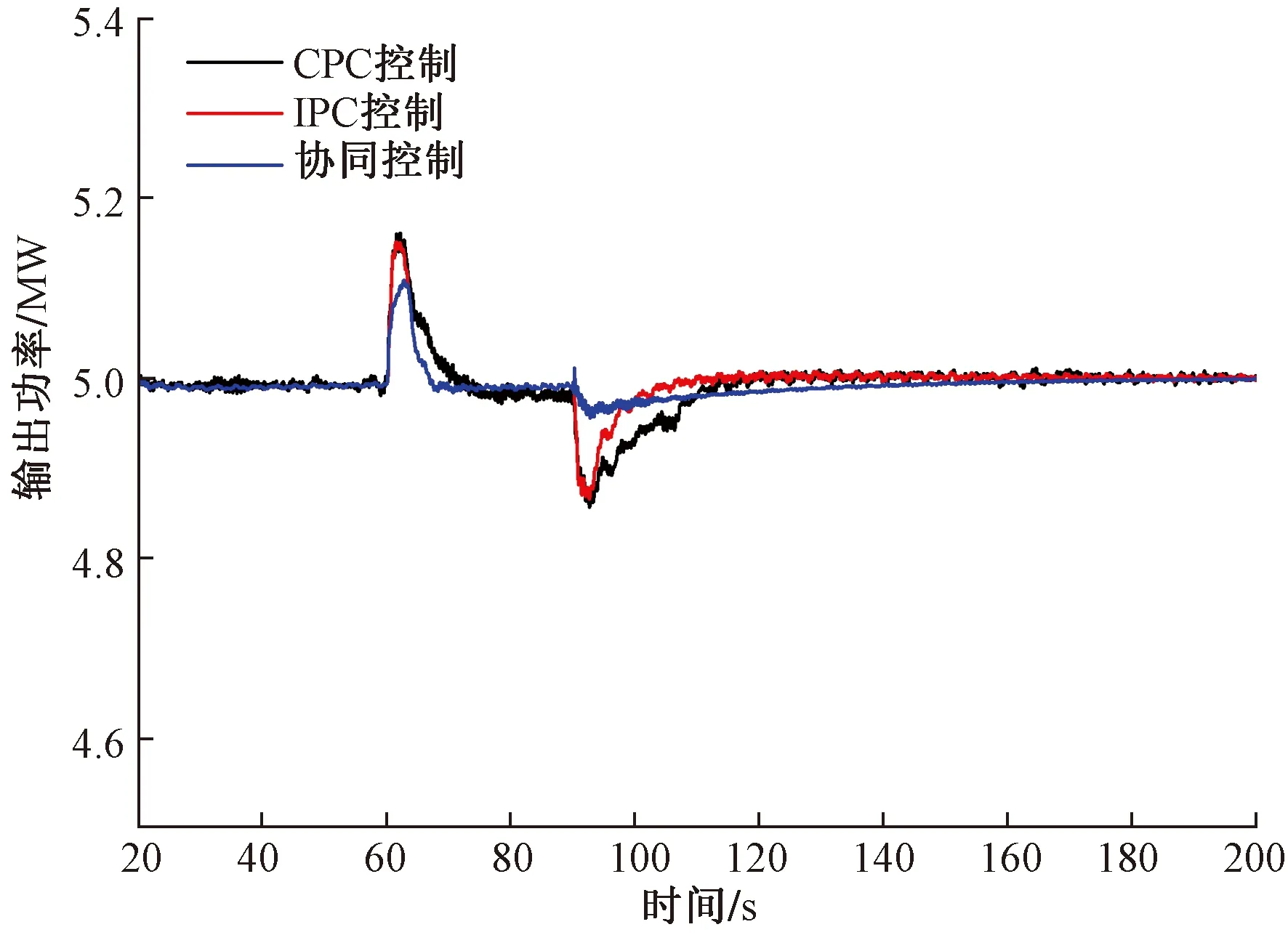
圖11 階躍風下輸出功率對比

3.3 載荷分析

在湍流風況下,對于三種不同控制策略,風機運行穩定后,選取20～70 s的葉根擺揮舞力矩My如圖12所示。由圖12可知,在相同風場條件下,相較于CPC控制和IPC-PI控制,協同控制對于降低葉根揮舞力矩的效果更為優越。為進一步分析各控制策略的優越性,對不同控制策略下的揮舞力矩各項指標定量分析,其結果如表3所示。

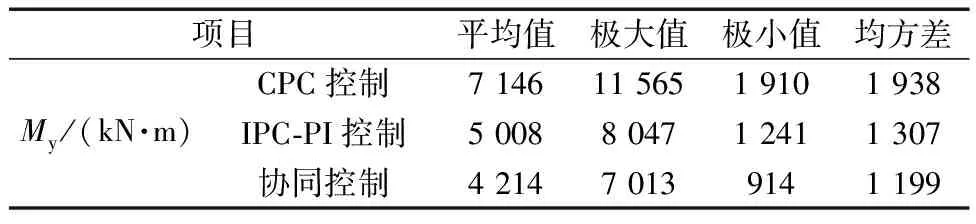
表3 各控制策略下揮舞力矩指標對比

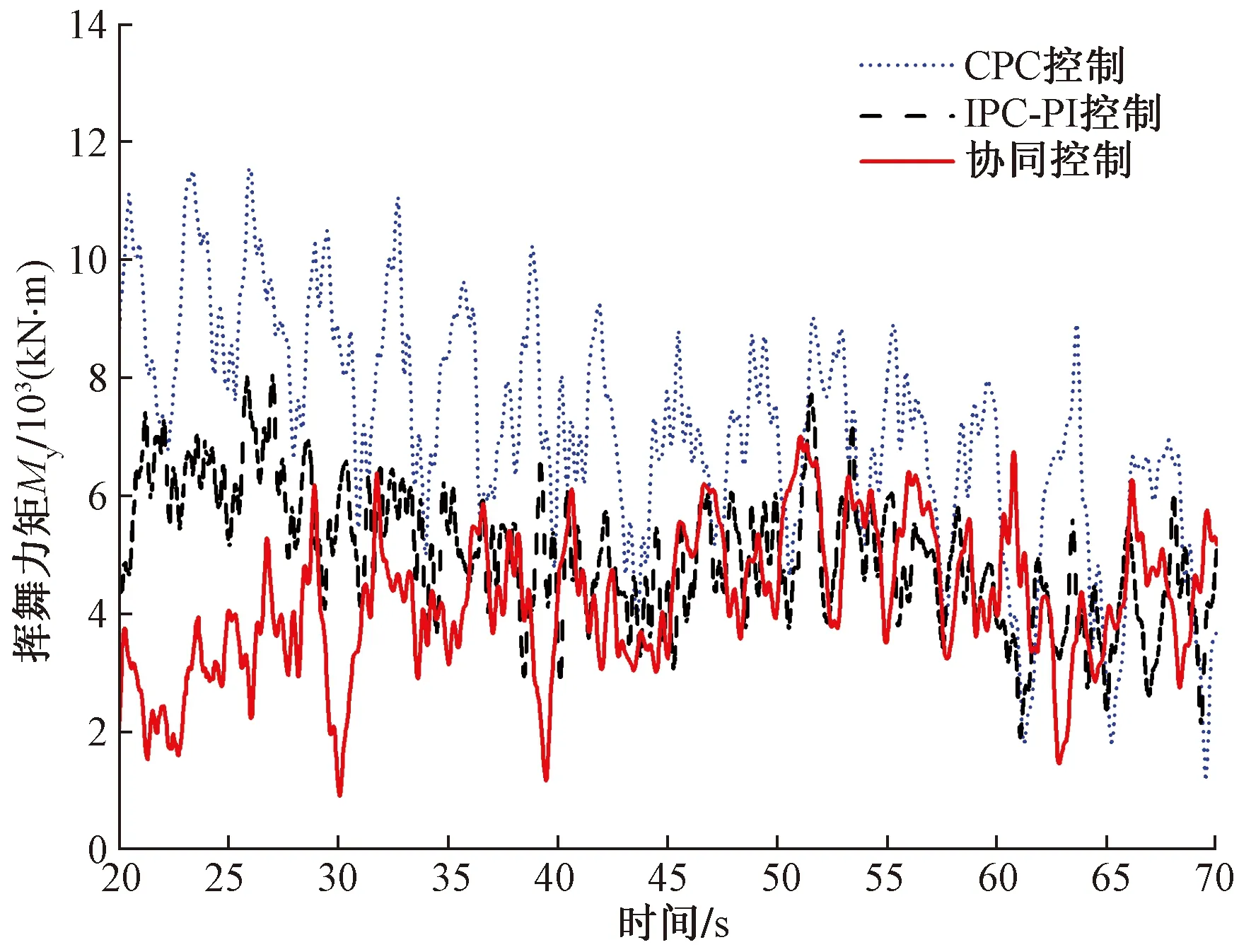
圖12 不同控制策略的葉根揮舞力矩My

從表3可知,相對于CPC控制和IPC-PI控制,在協同控制下,揮舞力矩的平均值、極大值和極值分別為4 214、7 013和914 kN·m,均小于前兩者控制,且與CPC控制和IPC控制相比,所提控制策略對揮舞力矩的均方差分別降低了38%和8%。

各控制策略下20～70 s的傾覆力矩和偏航力矩的對比如圖13和圖14所示。

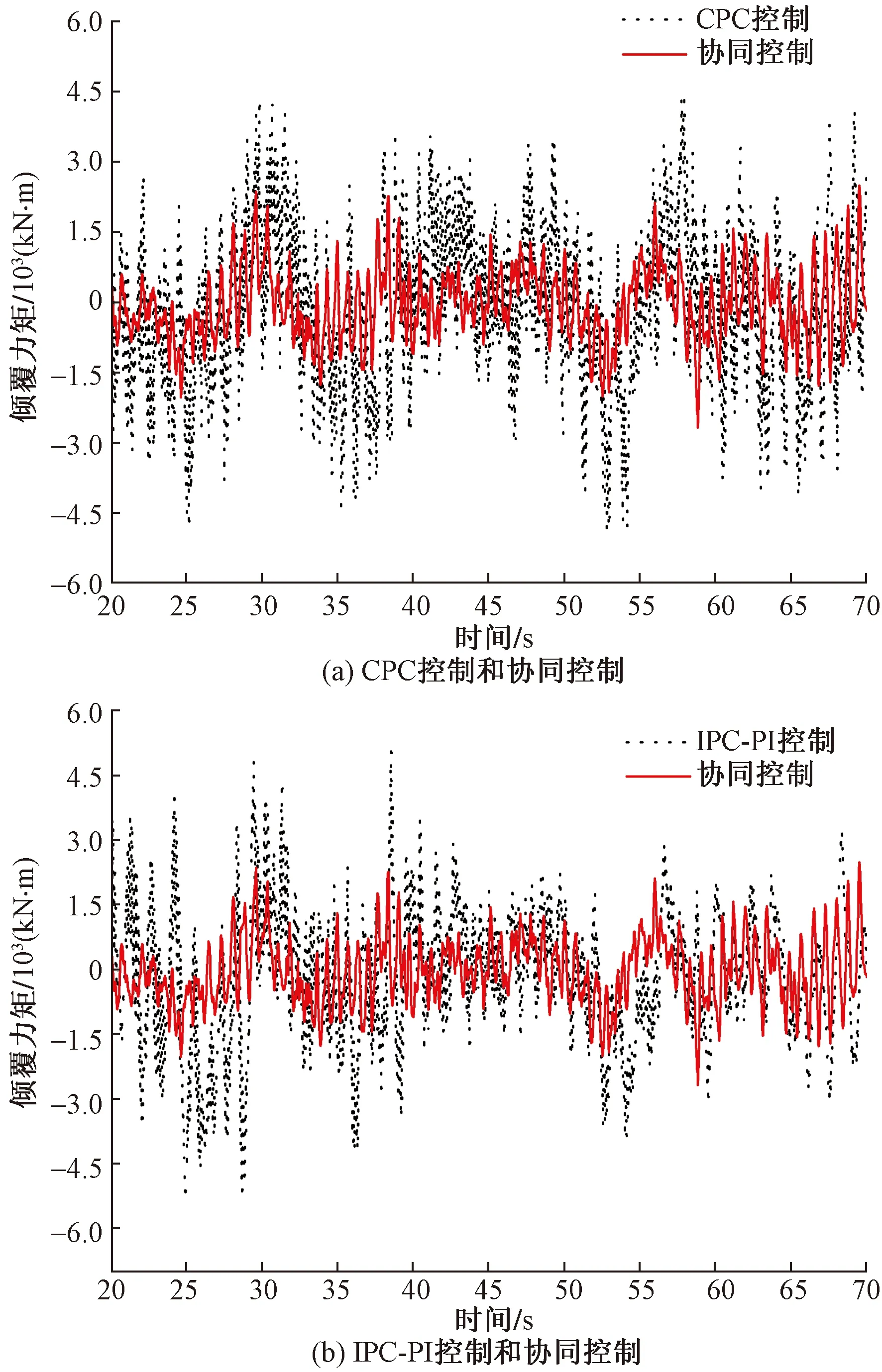
圖13 不同控制策略傾覆力矩對比

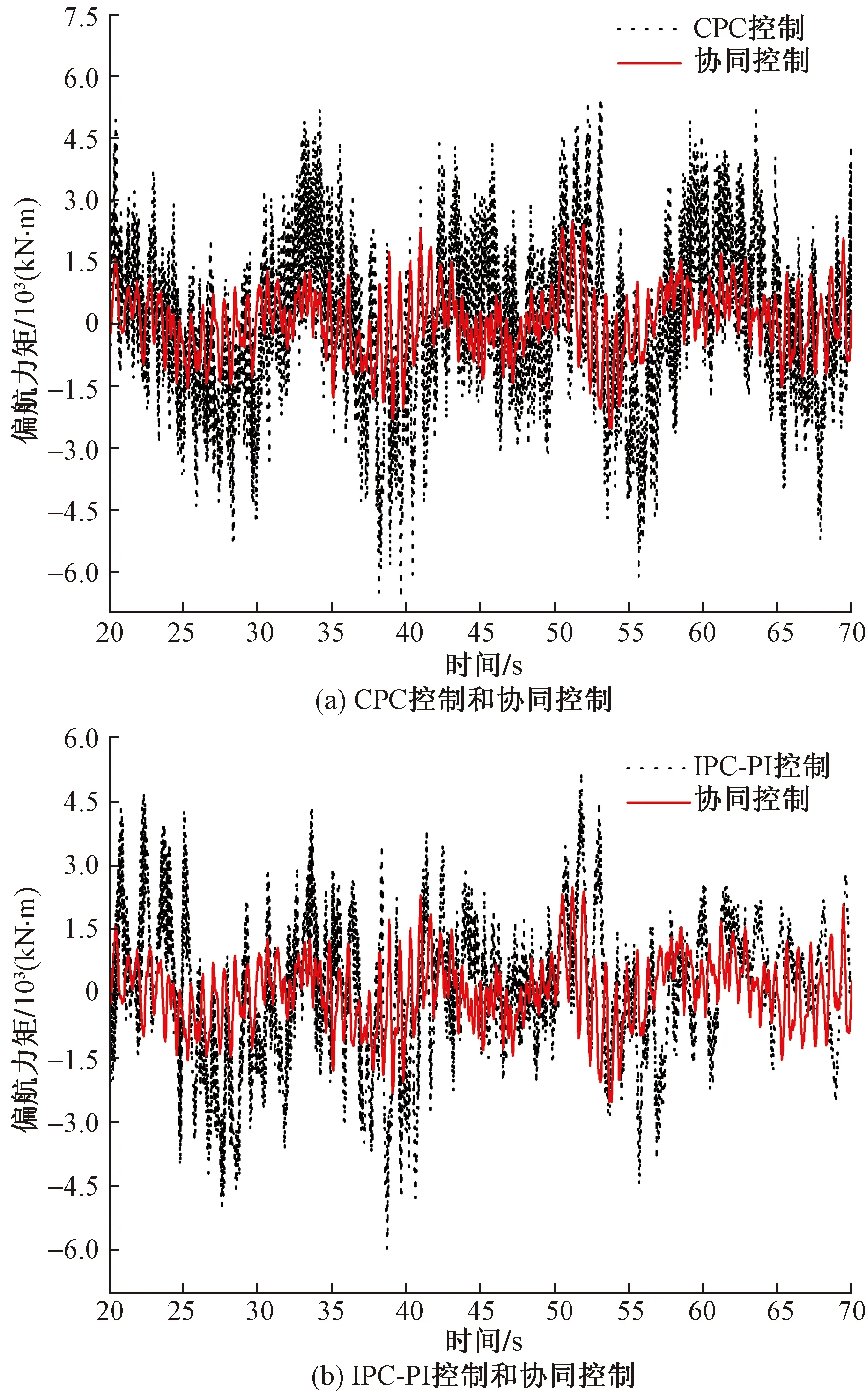
圖14 不同控制策略偏航力矩對比

各控制策略下傾覆力矩和偏航力矩對應的性能指標分別如表4和表5所示。

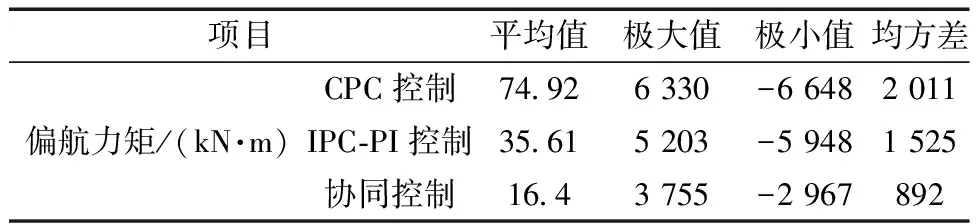
表5 各控制策略下偏航力矩指標對比

由圖13和圖14可知,協同控制對風機傾覆力矩和偏航力矩均能起到抑制作用,且相較于CPC控制和IPC-PI控制,協同控制其控制更為優越;由表4和表5可知,協同控制對于降低傾覆力矩和偏航力矩的平均值,抑制其極值的效果比CPC控制和IPC-PI控制更優越,且與前兩種控制策略相比,協同控制對傾覆力矩的均方差分別降低了52%和43%,對偏航力矩的均方差分別降低了55.6%和41.5%。

在階躍風況下,對于三種不同的控制策略,風機穩定后取40～120 s的傾覆力矩和偏航力矩對比如圖15和圖16所示。

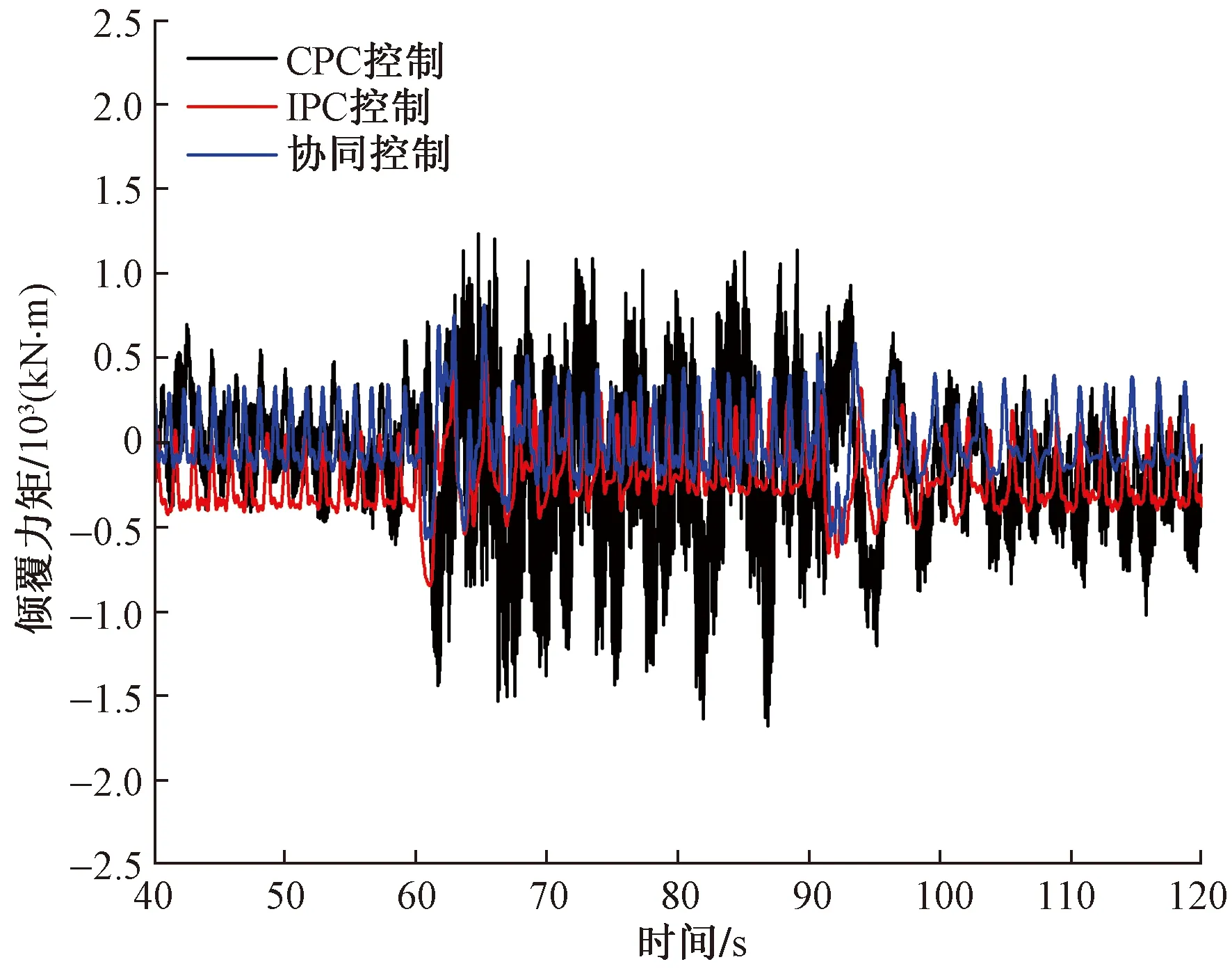
圖15 不同控制策略傾覆力矩對比

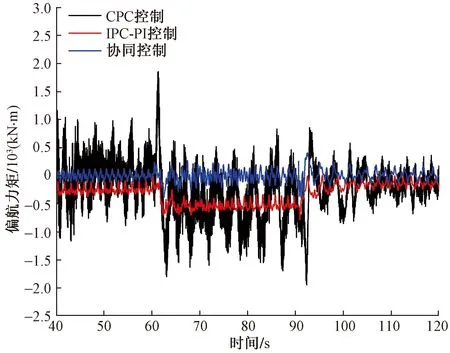
圖16 不同控制策略偏航力矩對比

從圖15和圖16可知,在階躍風況下,相較于CPC控制和IPC-PI控制,協同控制策略對于傾覆力矩和偏航力矩的抑制效果更為理想。為進一步分析其控制效果,對不同控制策略下的傾覆力矩和偏航力矩各項指標定量分析,其結果如表6和表7所示。

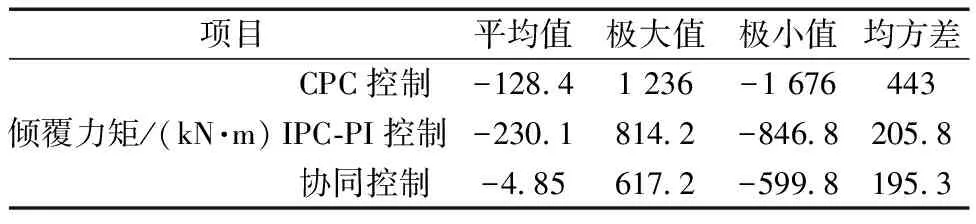
表6 各控制策略下傾覆力矩指標對比

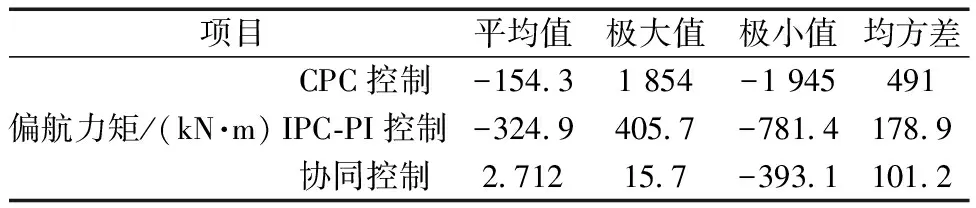
表7 各控制策略下偏航力矩指標對比

由表6和表7可知,在階躍風況下,相較于CPC控制和IPC-PI控制,協同控制對于降低傾覆力矩和偏航力矩的均值,抑制其極值的效果依然更為優越。且在協同控制下,傾覆力矩和偏航力矩的均方差更小。

綜上所述,在不同風況下,協同控制在抑制載荷和穩定輸出功率方面,其表現更為理想。

4 結論

隨著風機的大型化發展,風機槳葉半徑不斷增大,由此導致大型風機在高風速區輸出功率波動大,風輪不平衡載荷激增,對于風機的安全運行產生消極影響。為此提出一種功率和載荷雙目標協同控制的獨立變槳控制策略,并基于FAST和MATLAB/Simulink平臺進行聯合仿真,得到了較為理想的控制效果,仿真結果表明:

(1)在穩定風機輸出功率方面,所提控制策略相較于CPC控制和IPC-PI控制能更好地將輸出功率穩定在5 MW附近,且對于風速突變有較好的適應性,證明了該方法在穩定輸出功率方面的有效性。

(2)在降低不平衡載荷方面,協同控制能有效地降低葉根揮舞力矩、傾覆力矩和偏航力矩的平均值和極值,且控制效果明顯優于CPC控制和IPC-PI控制。證明所提方法在抑制不平衡載荷方面的有效性。

(3)相較于單個維度的控制策略,功率和載荷協同控制在兩個維度均取得了更優異的表現,且所提控制策略在不同風況下表現出了良好的適應性,這也證明了多維度控制策略的可行性。