基于應變補償的G13Cr4Mo4Ni4V軸承鋼本構行為

蔣小娟, 胡蒙均, 孫 濤, 肖欣睿, 董夢瑤, 張海成,3

(1. 重慶工業職業技術學院 機械工程與自動化學院, 重慶 401120;2. 重慶大學 材料科學與工程學院, 重慶 400044;3. 中國第二重型機械集團德陽萬航模鍛有限責任公司, 四川 德陽 618000)

隨著社會經濟的發展及科學技術的不斷進步,航空航天領域的發展受到世界各國的廣泛關注,航空發動機作為航空飛行器的動力源,對航空器的安全穩定服役起著至關重要的作用[1-2]。近年來,航空發動機逐漸向高推重比、高可靠性、強耐久性及低成本方向發展,使其結構和功能的復雜程度越來越高,發動機主軸服役環境也變得十分惡劣,因而對其設計和各功能部件的選材提出了更高的要求[3],基于此,針對航空發動機主軸軸承在極端環境下的運轉精度和使用壽命提出了新的挑戰[4]。各國目前均已研制出多種滿足航空軸承運行及使用要求的軸承鋼材料,其中M50軸承鋼是我國航空發動機主要使用的軸承鋼之一,其主要合金元素包括Cr、Mo、V等,這3種元素可以與鋼中的碳原子形成穩定的碳化物溶于基體中,形成固溶強化,在隨后的熱處理冷卻過程中析出形成彌散分布的第二相[5]。由于M50鋼變形溫度高、熱穩定性差、熱加工窗口窄,在實際鍛造過程中容易出現裂紋導致產品報廢或影響使用壽命[6-8]。G13Cr4Mo4Ni4V軸承鋼是在M50鋼的基礎上降低了C含量,提高了合金元素,如Ni、V等的含量,從而使基體中的碳化物分布更加均勻細小,避免形成大塊狀或網狀碳化物對構件沖擊性能的影響,增加V、Ni等元素含量還可以在一定程度上增加其耐蝕性能,保證其服役過程的穩定性,避免裂紋產生[9-10]。

針對G13Cr4Mo4Ni4V軸承鋼,國內外學者已進行了一些研究,例如Beer等[11]采用增材制造方法制備G13Cr4Mo4Ni4V軸承鋼,并對其力學性能開展研究,為軸承鋼的制造提供了新方法。Zhang等[12]采用Gleeble-3500熱模擬試驗機對比分析了不同初始組織對其流動行為及再結晶過程的影響,結果表明粗晶試樣的再結晶激活能和再結晶臨界應變高于細晶材料,細晶材料中含有大量彌散分布的第二相,在后續再結晶過程中可以抑制晶粒的長大,釘扎晶界,從而抑制晶界的遷移及原子的擴散,為異種材料的制備提供參考。丁開勇等[13]研究了熱變形參數對動態再結晶行為的影響,變形溫度為1100 ℃、變形量為60%時,隨應變速率的增大,再結晶形核率逐漸增大。李紅斌等[14]采用熱模擬試驗研究了熱變形的流動應力,建立了基于摩擦修正的J-C本構方程,其預測精度高于傳統的J-C模型。

G13Cr4Mo4Ni4V軸承鋼作為航空發動機主軸的主要軸承材料,其制造工藝過程尤為重要,目前對G13Cr4Mo4Ni4V軸承鋼的研究主要集中在熱變形過程中的再結晶行為,對其熱變形中的流動應力及加工過程的失穩區域進行研究顯得格外重要。本文采用等溫熱模擬試驗針對材料在熱壓縮過程中變形溫度和變形速率對應力的影響進行分析,并考慮了應變對本構模型參數的影響,建立了基于應變補償的Arrhenius模型,結果能夠很好地預測高溫下的流變應力,并建立了G13Cr4Mo4Ni4V軸承鋼的熱加工圖,對其生產工藝具有一定的指導意義,同時為數值模擬提供數據支撐。

1 試驗材料與方法

1.1 原始材料及組織

熱壓縮試驗材料來源于某鋼廠提供的棒材,材料經鍛造和均勻化退火處理,其元素主要含量如表1所示,圖1為退火態G13Cr4Mo4Ni4V軸承鋼的顯微組織(腐蝕劑為4%HNO3+酒精溶液),采用晶粒分析軟件可知,退火態的平均晶粒尺寸為20 μm,由圖1可知,退火后全部為珠光體組織和分布在基體中的碳化物,全部退火為大角度晶界組成的再結晶組織。

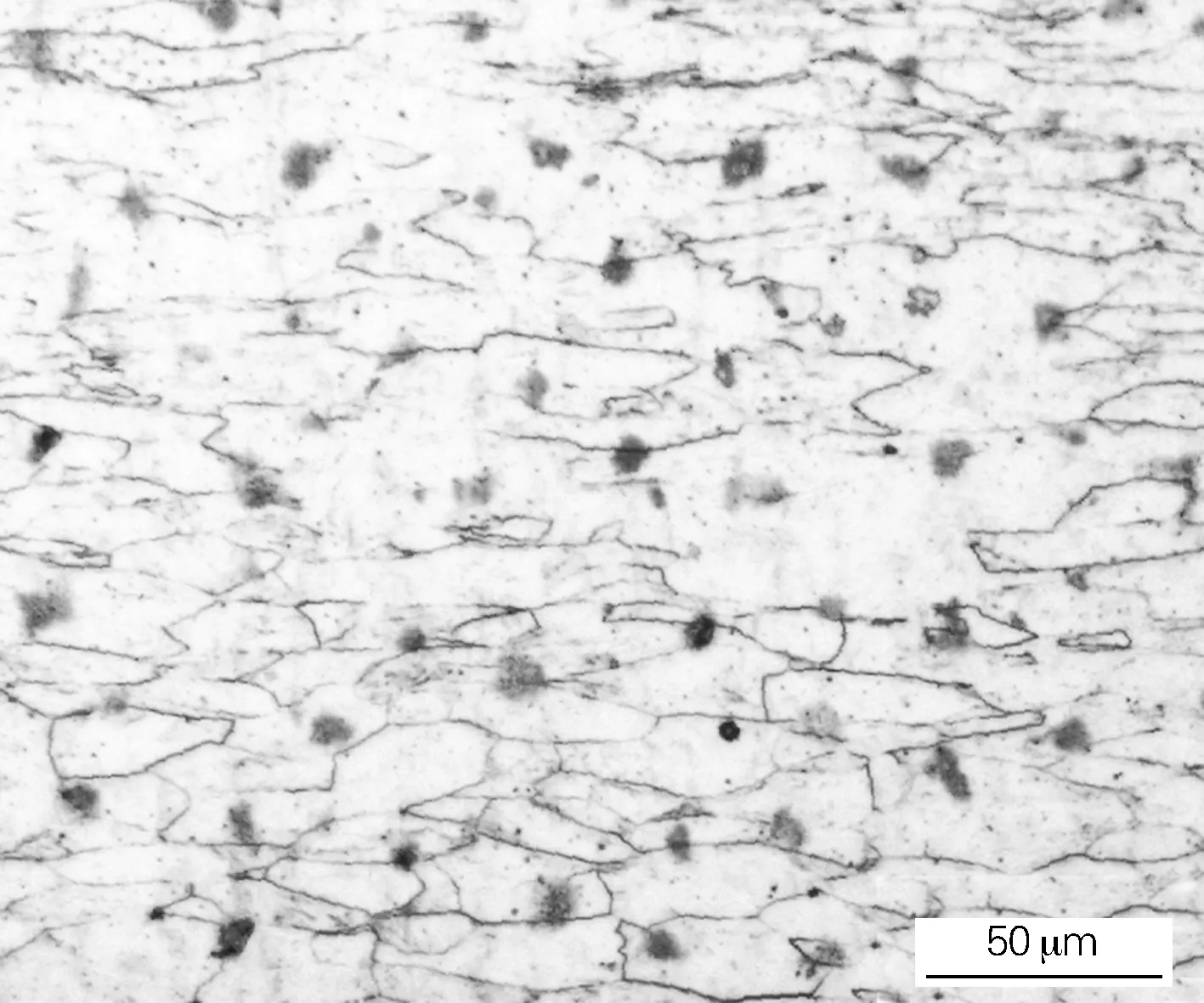
圖1 退火態4Cr4Mo3Ni1V鋼的顯微組織Fig.1 Microstructure of the annealed 4Cr4Mo3Ni1V steel

表1 G13Cr4Mo4Ni4V軸承鋼的化學成分(質量分數,%)

1.2 熱壓縮試驗

將退火后的棒料切割成φ8 mm×12 mm的圓柱形試樣,使用Gleeble-3800熱模擬試驗機進行等溫壓縮試驗,為減小摩擦對試驗數據產生的影響,提高試驗精度,試驗前先用砂紙將試樣兩側端頭進行打磨,然后在試樣與壓縮機的接觸部位粘貼石墨片,具體試驗過程如圖2所示,以10 K/s的加熱速率將試樣加熱至指定的試驗溫度(1223～1423 K),保溫3 min,確保試樣內部組織均勻化,然后以設定的應變速率對試樣進行壓縮,具體應變速率為0.001～1 s-1,總變形量為50%(真應變為0.7),變形后試樣空冷至室溫。

圖2 熱壓縮試驗示意圖Fig.2 Schematic diagram of hot compression experiment

2 試驗結果與分析

2.1 熱變形行為

不同變形溫度、應變速率下4Cr4Mo3Ni1V鋼的真應力-真應變曲線如圖3所示。由圖3可知,變形溫度相同時,其流變應力隨應變速率的增大而顯著增大,而變形速率相同時,流變應力隨變形溫度的升高而降低。金屬流變應力與應變、應變速率和溫度有關。力學或冶金參數會改變流動應力的結果。合金元素的加入提高了合金的流變應力,降低了合金的熱加工性能。一般情況下,應力-應變曲線的性質由變形溫度、應變速率、顯微組織和最終晶粒尺寸決定[15]。

圖3 不同變形溫度、應變速率下4Cr4Mo3Ni1V鋼的真應力-真應變曲線Fig.3 True stress-true strain curves of the 4Cr4Mo3Ni1V steel under different deformation temperatures and strain rates(a) 1223 K; (b) 1273 K; (c) 1323 K; (d) 1373 K; (e) 1423 K

圖4為4Cr4Mo3Ni1V鋼峰值應力隨變形溫度和應變速率的變化關系,峰值應力隨應變速率增大而升高,隨變形溫度升高而降低。變形溫度為1223 K、應變速率為0.001 s-1時峰值應力為118.39 MPa,變形溫度升高至1423 K時,峰值應力降低為42.78 MPa,相同變形溫度下應變速率從0.001 s-1增大至1 s-1時,對應的峰值應力為250.4 MPa。

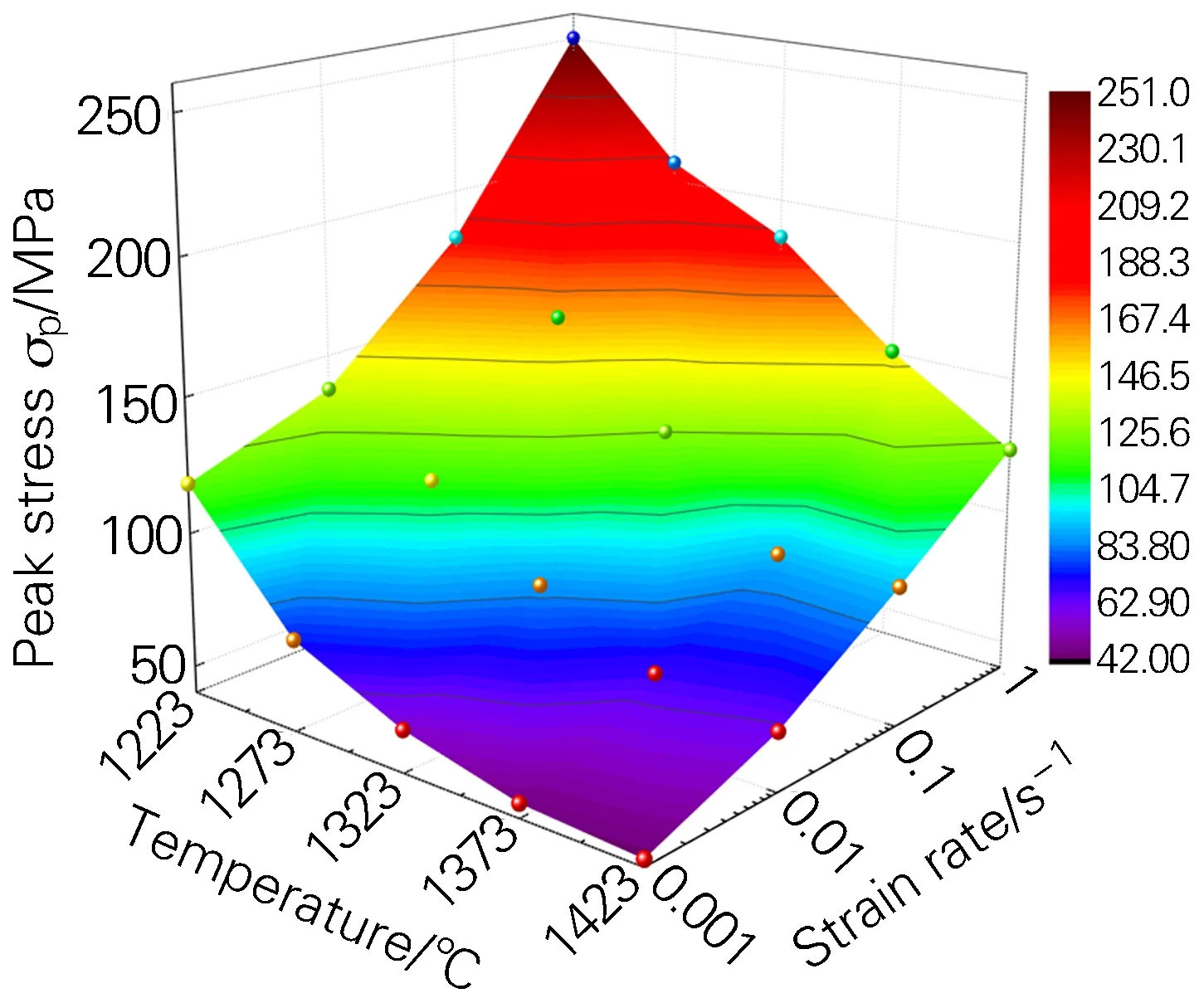
圖4 4Cr4Mo3Ni1V鋼峰值應力與變形溫度和應變速率之間的關系Fig.4 Relationship between peak stress, deformation temperature and strain rate of the 4Cr4Mo3Ni1V steel

進一步分析流動應力與變形溫度、應變速率、應變3者之間的關系可知,在壓縮變形的初期真應力隨應變的增加而迅速增大,當應變繼續增大時,應力達到最大值后不再增大,熱變形行為變為動態回復與動態再結晶兩種機制[16]。變形溫度較低且應變速率較高時,流動應力隨應變的增大先增大,隨著應變進一步增大,加工硬化導致的位錯密度增加與回復過程中位錯運動導致的密度下降達到平衡,流動應力保持不變。當變形溫度較高且應變速率較大時,變形儲能進一步增大,回復階段位錯運動形成的亞晶逐漸長大發展成為再結晶的晶核,由于再結晶過程生成了許多無畸變的晶粒,流動應力減小,直到達到穩態并保持恒定,這種軟化機制屬于動態再結晶機制。

2.2 本構方程

材料在高溫塑性條件下可使用Arrhenius模型來表示應力、應變速率和變形溫度3者之間的關系,目前該模型也是應用最為廣泛的材料熱變形本構方程。國外學者Sellars和McTegart[17]首次提出Arrhenius模型公式:

(1)

應力水平較低時(ασ≤0.8),

(2)

應力水平較高時(ασ≥1.2),

(3)

式中:A1、A2、n1、β為與溫度無關的材料常數,其中A1=Aαn1,A2=A/2n,β=αn1。

對式(2)和式(3)兩邊同時取自然對數可得式(4)和式(5):

(4)

(5)

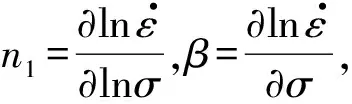
圖5 不同變形溫度和應變速率下4Cr4Mo3Ni1V鋼的和曲線Fig.5 Curves of and (b) of the 4Cr4Mo3Ni1V steel under different deformation temperatures and strain rates

一般情況下,變形激活能Q在一定溫度范圍內與T無關,對式(1)兩邊同時取自然對數可得:

(6)

在一定變形溫度下,對式(6)求偏微分,可得出變形激活能Q的計算式為:

(7)

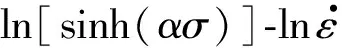
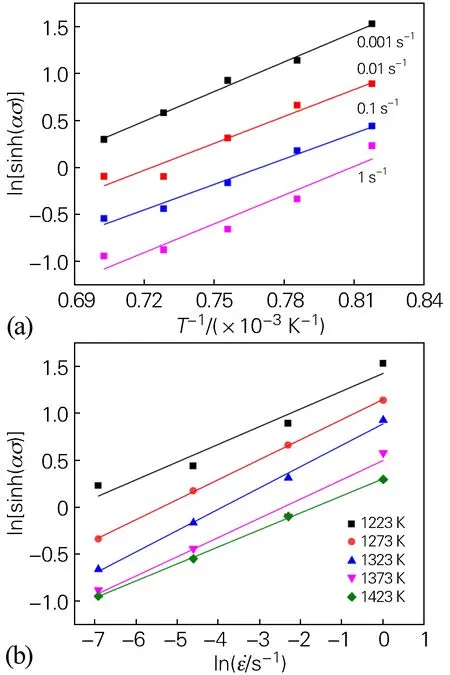
圖6 不同變形溫度和應變速率下4Cr4Mo3Ni1V鋼的和ln[sinh(ασ)]-1000×T-1(b)曲線 ln[sinh(ασ)]-1000×T-1(b) of the 4Cr4Mo3Ni1V steel under different deformation temperatures and strain rates

(8)

式中:Z為Zener-Hollomon參數,物理意義為溫度補償的應變速率因子。對式(8)兩邊取自然對數可得:

lnZ=lnA+nln[sinh(ασ)]

(9)

針對式(9)做lnZ-ln[sinh(ασ)]的關系曲線,見圖7所示,對其進行線性回歸可得lnA=31.5489,A=5.03×1013。由式(8)可得式(10):

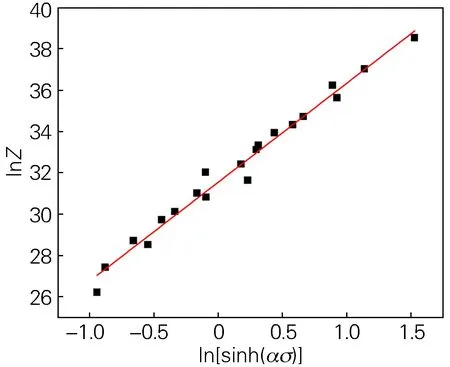
圖7 不同變形溫度及應變速率下4Cr4Mo3Ni1V鋼的lnZ-ln[sinh(ασ)]曲線Fig.7 lnZ-ln[sinh(ασ)] of the 4Cr4Mo3Ni1V steel under different deformation temperatures and strain rates

(10)

根據雙曲正弦函數sinh(x)的定義可以推出式(11):

(11)

根據式(9)～(11)可以將σ表示為Z的函數,如式(12)所示:

(12)

基于以上求解過程,峰值應變下的Q、n、α、lnA值已經分別得出,如表2所示,可將其與式(8)和式(12)結合,對流動應力值進行預測。

表2 高溫變形過程中峰值應變下的材料常數值

通過對G13Cr4Mo4Ni4V軸承鋼的本構方程求解過程發現,對于某一應變下的流動應力,可以使用該方程進行很好地預測,但在求解材料常數時,必須考慮不同應變對流動應力大小的影響,即需要對傳統的Arrhenius本構模型進行應變修正補償[21]。采用之前的方法分別計算出應變在0.05～0.7,間隔為0.05,共14個應變值對應的材料參數,如表3所示。

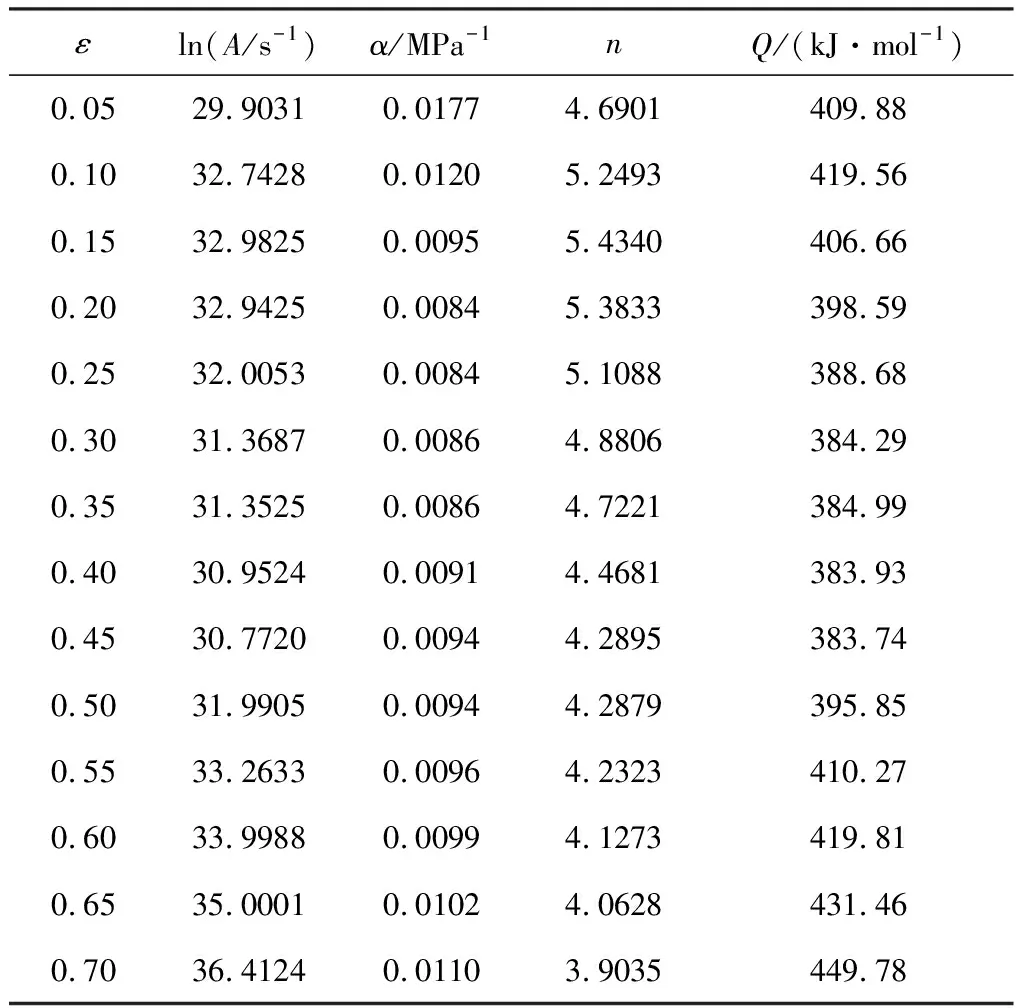
表3 G13Cr4Mo4Ni4V軸承鋼不同真應變對應的材料參數

根據計算出的上述4個材料參數并結合合金在高溫變形中常用本構擬合方法,本文采用八階多項式對上述參數分別進行擬合,以提高本構模型精度,擬合多項式采用如下矩陣模型進行表示:

(13)

材料參數lnA、α、n、Q采用多項式擬合結果如圖8(a～d)所示,多項式各項參數如表4所示,由擬合曲線可知,各多項式相關系數R2值均大于0.99,表明采用八階多項式擬合精度較好。

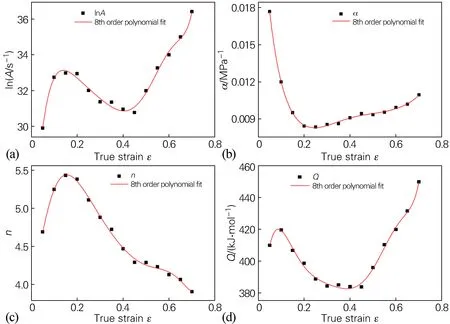
圖8 G13Cr4Mo4Ni4V鋼的八項式擬合結果Fig.8 Octomial fitting results of the G13Cr4Mo4Ni4V steel(a) lnA-ε; (b) α-ε; (c) n-ε; (d) Q-ε

表4 G13Cr4Mo4Ni4V鋼的材料參數八次多項式擬合及R2值

將表4中擬合出的材料參數的八階多項式代入式(6)中得:

(14)

根據Zener-Hollomon參數與Q的關系[22],將Q的擬合多項式代入式(8)中得:

(15)

根據式(14)和式(15)得到G13Cr4Mo4Ni4V軸承鋼考慮應變補償的Arrhenius本構模型:

(16)

2.3 本構模型的驗證及誤差分析

通過構建出的應變補償的本構方程計算不同應變速率、變形溫度和應變下的流動應力并與試驗值進行對比,如圖9所示。由圖9可以看出,該模型與試驗的流動應力能夠很好地吻合,尤其當變形溫度較高且應變速率較大時,預測值與試驗值擬合精度較高,可能是由于高溫及高應變速率下,等溫壓縮過程中引起的溫升對流動應力的擾動低于低溫低應變速率對其產生的影響[23]。

圖9 不同應變速率下試驗鋼應力試驗值與預測值的對比Fig.9 Comparison of test values and predicted values of stress of the tested steel under different strain rates(a) 0.001 s-1; (b) 0.01 s-1; (c) 0.1 s-1; (d) 1 s-1

為了進一步分析模型預測精度并對比試驗數據,使用相關系數R及平均相對誤差絕對值AARE(Average absolute relative error)分析預測值與試驗數據的相關性,統計參量的計算公式為[24]:

(17)

(18)

圖10 流動應力預測值與試驗數據相關性Fig.10 Correlation between predicted and experimental data of stress

3 熱加工圖

材料在特定的應變量水平下,其流動應力受變形溫度、應變速率、加工工藝條件等因素的影響,流動應力可采用式(19)表示[25]:

(19)

式中:K為常數;m為應變速率敏感指數;T為變形溫度;P為加工工藝條件。

材料在熱變形過程中,外界對其施加的總能量轉換為兩種形式進行耗散,分別為塑性變形所耗散的能量和微觀組織變化能量耗散[26-27],因此材料吸收的總能量采用式(20)表示,

(20)

式中:P為外界對工件所施加的能量;G為材料發生塑性變形所耗散的能量;J為微觀組織變化所消耗的能量。應變速率敏感因子m決定著G和J在P中所占比例關系:

(21)

根據以上兩式,微觀組織變化所耗散的能量與應變速率敏感因子存在如下關系:

(22)

當m=1時,微觀組織演變所耗散的能量達到最大值,此時J=G,定義功率耗散系數η,其物理意義為微觀組織演變所耗散的能量與線性耗散能量的比值:

(23)

(24)

(25)

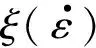
圖11給出了應變分別為0.2、0.4、0.6時,應變速率敏感因子m、功率耗散系數η以及失穩判據ξ隨變形溫度和應變速率不同而變化的等高線圖,通過對比可知,不同應變、變形溫度下,應變速率敏感因子m、功率耗散系數η以及失穩判據ξ分布規律大致相同。由圖11(b)可以看出,當應變為0.2時,功率耗散系數η存在兩個峰值區域,分別為1280～1400 K、0.001～0.0067 s-1和1340～1420 K、0.2231～1 s-1,對應的功率耗散系數η均處于0.3以上,失穩區域為低溫慢應變速率區域,對應溫度和應變速率為1223～1240 K、0.001～0.0067 s-1。當應變量增大到0.4時,對應功率耗散系數峰值區域擴大,最大值增大到0.35,對應的峰值區域分別為1300～1360 K、0.001～0.018 s-1和1350～1400 K、0.36～1 s-1,對應的失穩區域進一步縮小。應變從0.4增大0.6時,功率耗散系數第Ⅰ峰值區域幾乎不變,第Ⅱ峰值區域進一步擴大,且處于高溫高應變速率時,失穩區域也隨之縮小至失穩判據ξ值均處于0以上。合金材料在實際加工過程中,各部位均處于非均勻的變形狀態,需要盡可能多地結合應變分布及應變速率敏感因子m、功率耗散系數η以及失穩判據ξ等共同來決定合金最佳加工溫度與應變速率范圍[29-30]。根據以上數據,G13Cr4Mo4Ni4V軸承鋼在低溫及低應變速率下存在發生失穩的風險,且η值也較低。綜上,變形溫度在1320～1400 K、應變速率在0.1～1 s-1范圍內,該鋼具有較高的熱穩定性。

4 結論

1) 研究了G13Cr4Mo4Ni4V軸承鋼等溫熱壓縮過程中的流變應力與變形溫度、應變、應變速率等因素的關系,其流變應力表現為動態回復與動態再結晶兩種軟化機制,流變應力與應變速率呈正相關性,與變形溫度呈負相關性。

2) 研究了材料相關參數與應變的關系,結合八階多項式對本構方程中的相關參數進行擬合,擬合出的相關系數均高于0.95,并引入溫度補償的應變速率因子Z值,構建了考慮應變補償的Arrhenius本構方程,通過該方程將預測值與試驗數據進行對比,其相關系數R及平均相對誤差絕對值AARE分別為0.991和5.786%,擬合精度較高。

3) 分別研究了該軸承鋼在應變為0.2、0.4和0.6時的應變速率敏感因子m、功率耗散系數η以及失穩判據ξ值與變形溫度和應變速率的關系,該軸承鋼在低溫及低應變速率下易出現失穩區域,且該區域功率耗散系數較低,變形溫度在1320～1400 K、應變速率在0.1～1 s-1范圍內,該鋼具有較好的熱加工性。