基于鞅驅動的時滯倒向隨機微分方程最優控制

周 敏,顏 瑞,李志民

(安徽工程大學數理與金融學院,安徽 蕪湖 241000)

0 引言

線性倒向隨機微分方程由BISMUT[1]首次提出,方程一般化面臨的一個問題是要解決方程的存在唯一性,此問題困擾學界很長時間.PENG[2]在利用線性倒向隨機微分方程研究隨機最大值原理問題時發現,解決強制性是推動倒向隨機微分方程的關鍵.隨后,PARDOUX和PENG[3]提出了一般形式的倒向隨機微分方程,解決了這個倒向隨機微分方程的研究瓶頸問題,PENG[4-6]在后期的系列工作建立了倒向隨機微分方程理論體系.

PENG的工作推動了倒向隨機微分研究的蓬勃發展,后繼學者圍繞如何解決方程中的生成元的結構和擴散部分開展研究,產生一系列成果.TANG和LI[7]討論了布朗運動和泊松過程混合驅動的倒向隨機微分方程,KAROUI等[8]研究由一般鞅驅動的倒向隨機微分方程.王湘君[9]研究了以連續局部鞅為干擾源的倒向隨機微分方程,在系數滿足Lipschitz條件下證明了其解的存在唯一性.李娟[10]在此基礎上研究了以一般鞅為干擾源的倒向隨機微分方程,對經典的倒向隨機微分方程進行實質性推廣,得到了其解的存在唯一性.一些學者嘗試弱化終端條件和生成元的Lipschitz條件來推廣PARDOUX和PENG的結論,FAN等[11]得到了非Lipschitz條件下倒向隨機微分方程解的存在唯一性;程中華[12]得到了非Lipschitz條件下和局部Lipschitz條件下由連續局部鞅驅動的倒向隨機微分方程的解的存在唯一性,并得到了其比較定理.DELONG等[13]考慮生成元在時間上可以依賴于過去的一個解的值,用一個時間延遲函數加權,給出了時滯倒向隨機微分方程的概念.CHEN等[14]考慮生成元不僅取決于瞬時狀態,還通過時滯參數取決于過去的狀態,利用帶時滯生成元的倒向隨機微分方程和超前隨機微分方程之間的對偶性,證明了這兩類方程解的存在唯一性,導出了最大值原理的充要條件.

倒向隨機微分方程理論和方法逐漸被應用在金融產品的定價中,馮莎莎等[15]總結了期權定價模型,同時利用倒向隨機微分方程推導期權定價公式.馬玉東[16]通過對倒向隨機微分方程進行保險定價公式的合理改進,加入了公司營業費用率和未決賠款準備金比率的參數調整,使之更加符合保險公司的實際經營情況.徐銘浛[17]利用倒向隨機微分方程求解連續支付紅利的期權定價,苗杰[18]用BSDE理論得到了可分離債券價格所滿足的倒向隨機微分方程,得出了可分離債券價格的顯式公式.在CHEN等[14]的研究中,方程是在布朗運動驅動下的倒向隨機微分方程,具有較強的限制條件,而在實際問題中尤其是在金融問題中,布朗運動往往不是刻畫股票價格過程的理想工具[19].為此,本文考慮了更加一般的情況,對驅動過程進行推廣,將連續鞅驅動的倒向隨機微分方程與時滯結構結合起來,考慮由連續鞅驅動的時滯倒向隨機微分方程和與之對偶的連續鞅驅動的超前隨機微分方程,利用解的存在唯一性,時滯倒向隨機微分方程生成元可以依賴過去的狀態,從而可用于股票價格具有時滯效應的期權定價、保險費率計算等,在決策和控制中亦有應用的可能.

1 準備知識

其中,y(t)是一個-適應的Rn-值的過程.當n=1時上式簡記為LM.

其中,z(t)是一個-可料的Rn-值的過程.當n=d=1時上式簡記為

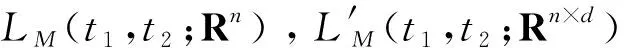
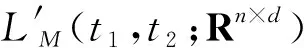
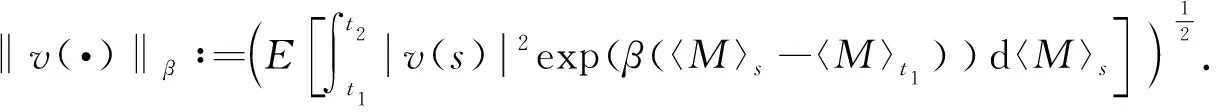
考慮以下時滯倒向隨機微分方程(BSDE):

(1.1)

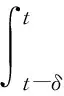
假設方程系數滿足如下條件:

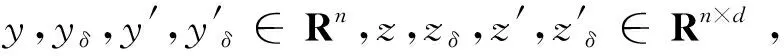
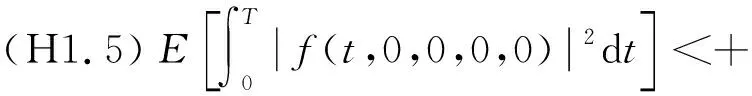
考慮以下形式的超前隨機微分方程:

(1.2)

其中,對于?t∈[0,T],r∈[t,T+δ],有

且滿足下列假設:

(H2.1)存在一個常數C3>0,使得對于所有的t∈[0,T],x,x′∈Rn,ζ(·),ζ′(·)∈LM(t,T+δ;Rn),r∈[t,T+δ],有

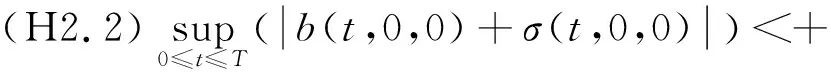
2 解的存在唯一性

對于由方程(1.1)確定的具有時滯結構的由鞅驅動的倒向隨機微分方程,給出如下定理.

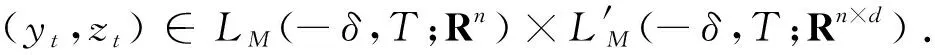
其中,a(β,s,t)=exp(β(〈M〉s-〈M〉t)).

令

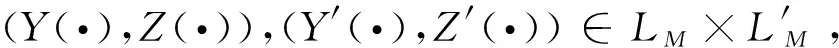
(y(·),z(·))=Φ[(Y(·),Z(·))],

(y′(·),z′(·))=Φ[(Y′(·),Z′(·))],

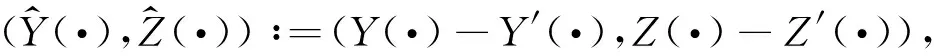
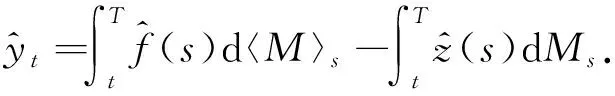
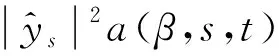
從而有

于是有

注意到,

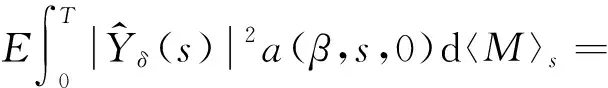
同理,

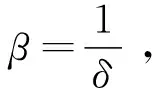
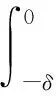
只要δ足夠小,就能保證K(C2,L,δ,α,β)<1,即

(y′(·),z′(·))=Φ[(Y′(·),Z′(·))]≤K(C2,L,δ,α,β)[(Y′(·),Z′(·))].

因此Φ在范數‖·‖β下就為一個壓縮映射,由不動點定理可知,定理2.1得證.

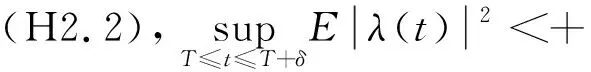
證明 類似于定理2.1的證明,定義以下范數,在Hilbert空間LM(0,T+δ;Rn)中構造壓縮映射:

其中,a′(β,s,t)=exp(-β(〈M〉s-〈M〉t)).

定義映射I:LM(0,T+δ;Rn)?LM(0,T+δ;Rn),使得I[X(·)]=x(·).對于任意的X(·),X′(·)∈LM(0,T+δ;Rn),記

I[X(·)]=x(·),I[X′(·)]=x′(·),

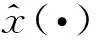
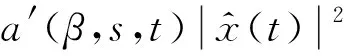
其中,

由b,σ滿足(H2.1),得到

于是,

注意到,

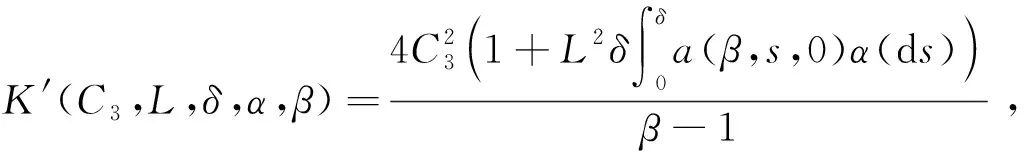
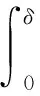
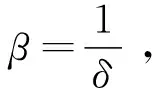
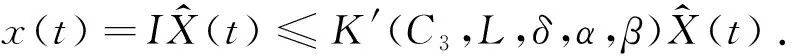
因此I在范數‖·‖β下為一個壓縮映射.由不動點定理可知,定理2.2得證.

3 解的最優控制

在金融領域,具有延遲盈余的養老金、具有時滯效應的股票期權定價與原保險費率等都可以用以下時滯倒向隨機微分方程進行刻畫.

(3.1)

其中,μ(t)表示資產在t時刻的回報率,σ(t)表示在t時刻的波動率.

方程(3.1)為線性的時滯倒向隨機微分方程,方程生成元包含當前t時刻和過去t-δ時刻解的值.可見方程(3.1)為方程(1.1)的特殊形式,由定理2.1可知其存在唯一解.

下面介紹與之對偶的超前隨機微分方程:

(3.2)

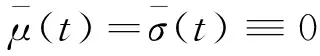
定理3.1 時滯倒向隨機微分方程(3.1)的解Y?可由以下閉式給出:

其中,X(s)是以下超前隨機微分方程的解:

(3.3)

證明 首先證明(3.3)有唯一解.當s∈[T-δ,T]時,(3.3)變為

(3.4)

易知(3.4)有唯一解λ?.當s∈[t,T]時,(3.3)變為

(3.5)

可見方程(3.5)是一個經典的超前隨機微分方程,由定理2.2可知,方程(3.5)存在唯一解.

對X(s)Y(s)在s∈[t,T]上應用It’s公式,

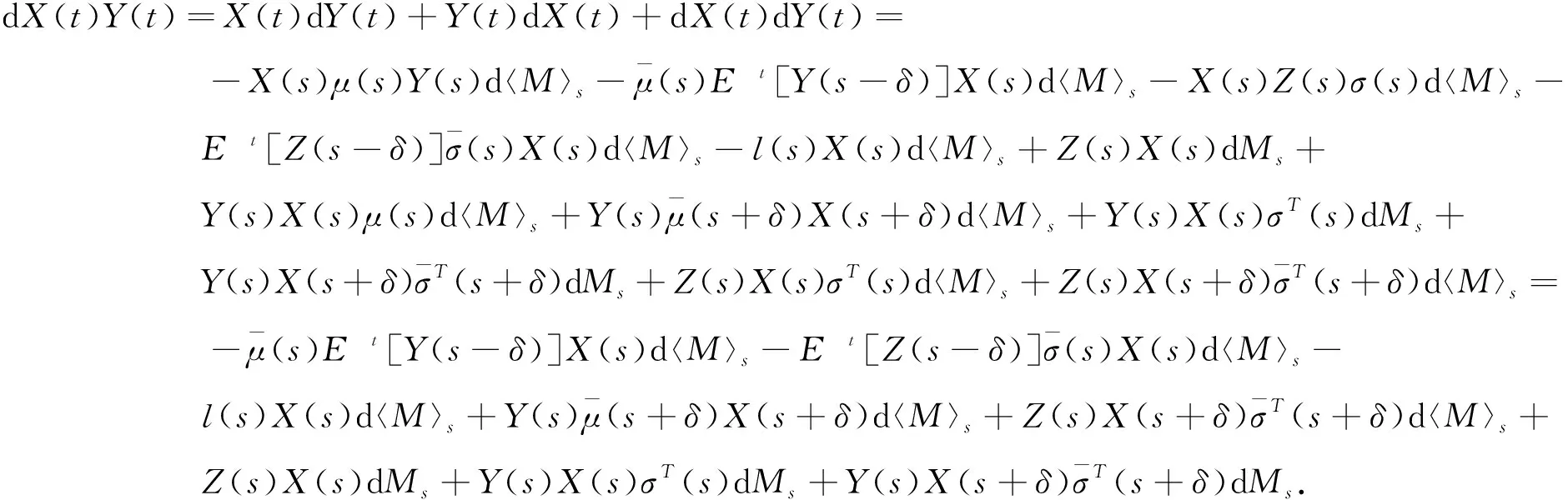
等式兩邊取條件期望,

由于X(t)=1,X(t)=0,s∈[T,T+δ],則有

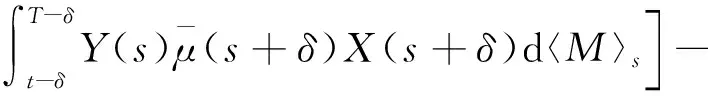
綜上所述,本文通過時滯倒向隨機微分方程與超前隨機微分方程之間的對偶性,將超前隨機微分方程作為伴隨過程,得出了解的最優控制,在具有延遲盈余的養老金動態最優、具有時滯效應的股票期權定價與原保險費率等前提下,可利用該最優控制方法解決金融產品定價問題.