基于自適應神經模糊推理系統及隨機分形搜索算法的黃酒發酵過程建模與優化
劉登峰,蔣國慶,許錫飚
1(江南大學 人工智能與計算機學院,江蘇 無錫,214122)2(紹興女兒紅釀酒有限公司,浙江 紹興,312352)
黃酒發酵的實質是一個多變量輸入、輸出的生物化學反應過程,麥曲、酵母、大米在不同環境條件下相互作用,生成了糖類、有機酸、乙醇、酯類、醛類、氨基酸等各種代謝產物[1-2]。黃酒發酵工藝主要分為傳統手工釀造、機械化釀造2種[3]。一方面,手工釀造依賴釀酒師的人工經驗,已逐漸不能適應工業化生產和控制的需求;另一方面,機械化新工藝的黃酒發酵過程難以實時監測和控制,黃酒品質穩定性差,其自動化水平落后于其他工業生產。2021年,《“十四五”智能制造發展規劃》中提出,加快輕工、食品行業的智能和綠色制造升級,如何實現黃酒發酵自動化控制是黃酒產業面臨的關鍵問題。
目前關于黃酒發酵自動化的研究主要分為2個方面。一是對發酵過程中的環境變量進行監測和控制。徐玲等[4]針對黃酒發酵過程中溫度控制存在的延遲問題,設計了數字式Smith預估增量比例-積分-微分(proportion integration differentiation,PID)控制器,但發酵過程中關鍵生物變量卻鮮有涉及;二是對黃酒發酵過程建立數學模型。LIU等[5-7]探討了4種酶、酒曲和3個發酵溫度對黃酒發酵過程中糖類、有機酸、甘油、乙醇的影響,為黃酒發酵的建模提供了理論基礎;針對發酵過程中主要生化反應和初級產物,提出了不同溫度條件下同時糖化發酵的動力學模型(simultaneous saccharification and fermentation,SSF);還針對工業生產中黃酒前酵階段,建立了工業生產中同時糖化發酵模型SSF,并采用Marquardt方法對模型參數進行了辨識;宗原等[8]針對基于Levenberg-Marquardt易陷入局部最優解,收斂速度慢的問題,提出了具有萊維飛行機制和柯西變異的蟻獅優化算法,提升了固定溫度條件下SSF模型的精度。一方面上述模型只適用于特定的溫度條件,模型的通用性不高;另一方面,黃酒發酵過程是非線性,基于發酵動力學的SSF模型的擬合效果較差。
針對上述黃酒發酵數學模型中的問題,本文分別從建模方法和優化方法2個維度進行了研究:a)在系統建模方法中,模糊系統由于其良好的可解釋性及強大的學習能力得到了廣泛的關注[9-11],其中自適應神經模糊推理系統(adaptive network-based fuzzy inference system,ANFIS)[9]將模糊邏輯與神經網絡結合,可以很好地處理非線性問題;b)在優化方法中,通過模擬自然界中生物行為或物理現象的元啟發式算法常被用來解決各種學科領域的最優化問題[12-19],常見的有粒子群算法(particle swarm optimization,PSO)[15]、隨機分形搜索算法(stochastic fractal search,SFS)[16]等。
本文針對黃酒發酵產物多樣性的特點,首先提出了多輸出自適應神經模糊推理系統(multi-output adaptive network-based fuzzy inference system,MOANFIS);其次將層次學習粒子群算法(level-based learning swarm optimizer,LLSO)[20]中的層次學習策略與萊維飛行結合,提出了層次學習的隨機分形搜索算法(level-based learning stochastic fractal search,LLSFS),該算法在面對高維優化問題時,具有優秀的全局搜索能力;最后,將LLSFS算法用于MOANFIS模型的優化,并與其他算法進行比較。
1 多輸出自適應神經模糊推理系統
ANFIS是基于T-S模糊系統[21]而建立的,既可以利用神經網絡的學習機制自動從輸入輸出數據中提取規則,又兼具有模糊系統清晰的語言表達能力,但是其只有一個輸出結點。黃酒發酵過程是一個多變量輸入、輸出的系統,本文將ANFIS的單維輸出拓展為多維輸出,即MOANFIS,其結構如圖1所示,其中長方形結點表示含有系統參數的自適應結點,圓形結點表示無系統參數的固定結點。
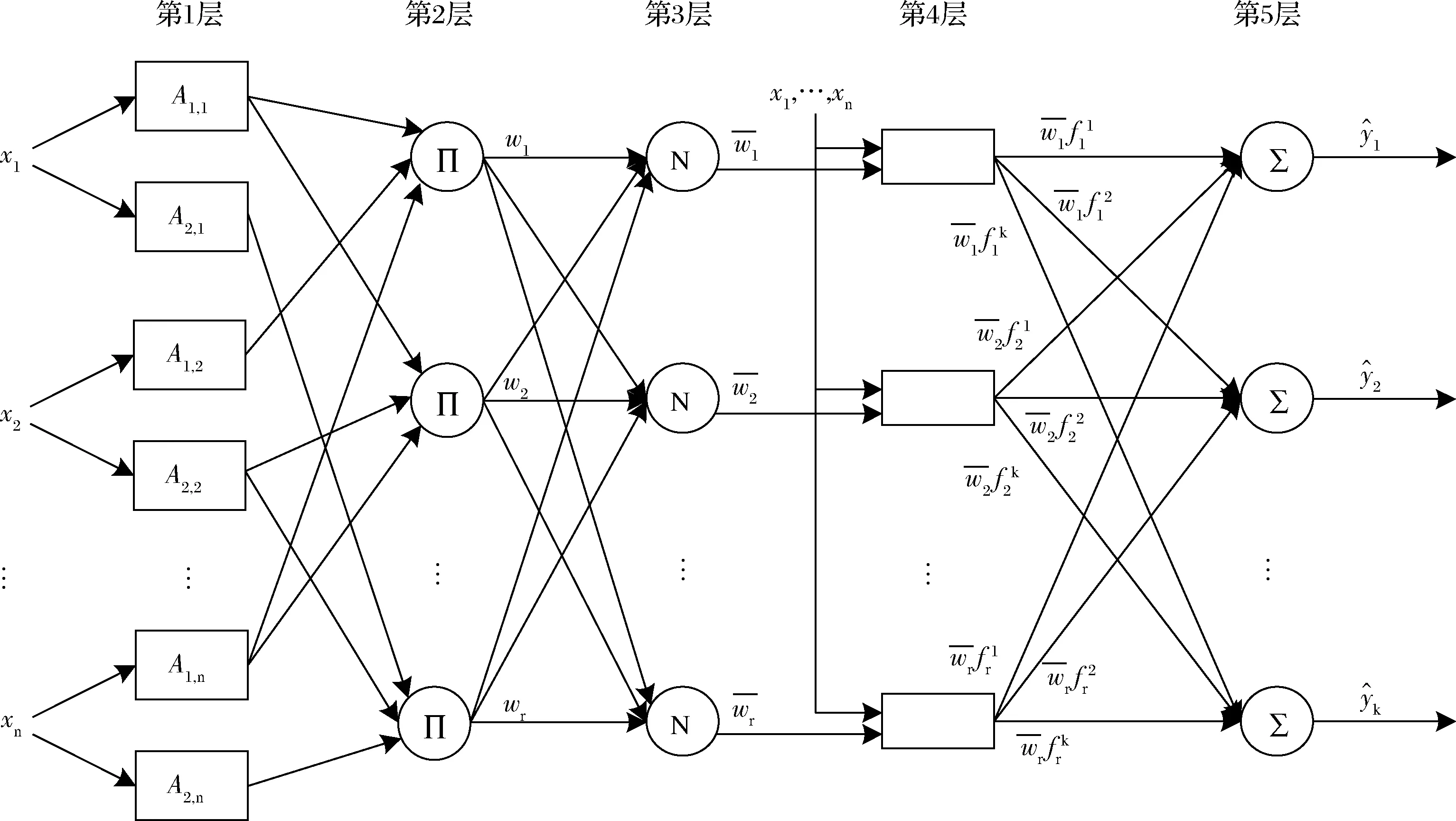
圖1 MOANFIS結構圖Fig.1 Structure of MOANFIS
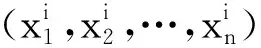
第1層:模糊層。對輸入數據進行模糊化操作,計算每個維度特征的隸屬度。本文選取高斯函數作為隸屬度函數,Ai,j(i=1,…,n;j=1,2)是每個特征對應的模糊集。該層輸出如公式(1)所示:
(1)
式中:cij,σij分別為高斯函數的均值和標準差,是模糊規則的前件參數。
第2層:規則的權重層。該層實現了模糊推理過程,每個節點的輸出表示某一條規則的可信度,如公式(2)所示:
(2)
第3層:規則的權重歸一化層,如公式(3)所示:
(3)
第4層:模糊規則輸出層。對于一個n維的輸入向量x=(x1,x2,…,xn),k維輸出向量的MOANFIS,其第l個規則表示如公式(4)所示:
(4)
式中:A1,j,A2,j,…,An,j(j=1,2)表示模糊子集,θ[l]∈R(n+1)×k表示是對應于k維輸出向量的第l個模糊規則的后件參數矩陣,所有模糊規則的后件參數矩陣為θ=(θ[1],θ[2],…,θ[r])∈Rr×(n+1)×k。每個模糊規則都共享模型的前件參數,本層輸出如公式(5)所示:
(5)
第5層:輸出層,如公式(6)所示:
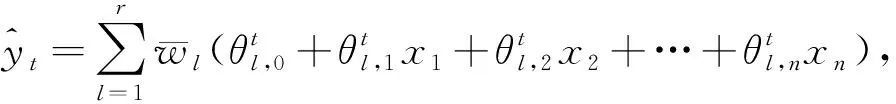
(6)
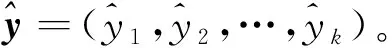

(7)
2 多輸出自適應神經模糊推理系統的優化
2.1 隨機分形搜索算法
SFS[16]是Salimi模仿自然界中的物理擴散現象提出的一種智能優化算法。簡單起見,初始粒子位于平面原點,然后往周圍隨機擴散生成其他粒子。重復這個過程,直到形成一個分支狀結構的簇。粒子分形過程如圖2所示。
圖2 粒子分形示意圖Fig.2 Demonstration of particle diffusion
FS算法主要有2個階段:分形階段和更新階段。前一個過程中,每個粒子在其當前位置周圍擴散,增加了找到優化函數全局最小值的機會,也避免了陷入局部最小值。后一種過程中,算法模擬了一個粒子根據其他粒子的位置更新自己的位置。為了避免粒子擴散導致粒子數量急劇增加,SFS考慮的是一個靜態擴散過程,即擴散過程中產生的最佳粒子是唯一被考慮的粒子,其余的粒子被丟棄,同時算法還使用了一些隨機方法參與更新的過程。詳細內容請參考原論文。
2.2 對隨機分形搜索算法的改進
SFS算法中第二階段的更新過程中,是基于最佳粒子或隨機挑選粒子對整個種群進行的更新。隨著優化問題維度的增加,局部最優解增多,粒子易陷入局部最優點而導致算法過早收斂。針對此問題,本文將LLSO[20]中的層次學習策略與萊維飛行結合后,改進了SFS中第二階段的對粒子的更新方式,提出了LLSFS算法。
2.2.1 層次學習策略
LLSO根據粒子對應的函數適應度值將其劃分成為不同的等級,好的粒子具有更高的等級,對應于更小的層級號。層次學習策略如圖3所示。
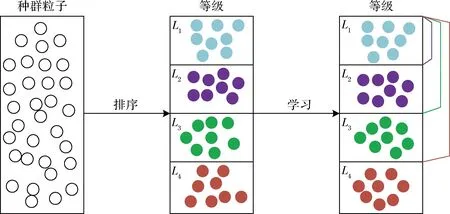
圖3 層次學習的結構圖Fig.3 Framework of Level-Based Learning
首先,粒子群中各粒子根據其對應的函數適應度值升序排列,并劃分成4個等級L1~L4。L4中的粒子向L1~L3中的粒子學習,L3中的粒子向L1~L2中的粒子學習,L2中的粒子向L1中的粒子學習,L1中的粒子不進行更新直接進入下一次循環中。粒子的更新方式如公式(8)所示:

(8)
式中:Pi,j位于第Li層的第j個粒子,Vi,j是其速度。Prl1,k1和Prl2,k2分別是從更高的2個層中rl1和rl2中隨機挑選出的2個粒子,k1和k2表示各自層中的粒子的索引值。Lrl1層級高于Lrl2層級,即Prl1,k1粒子優于Prl2,k2粒子。r1、r2和r3是[0,1]之間的隨機數,φ是[0,1]之間的隨機數。
層次學習策略具有以下特點:一方面,更高等級的粒子指引種群朝著全局最優解的方向進化,進而獲得較快的收斂速度;另一方面,處于低層級的粒子有著更強的空間探索性能表現。
2.2.2 萊維飛行的層次學習策略
為了更好地提升算法的全局搜索能力,避免早熟收斂,本文將萊維飛行融入層次學習策略中。萊維飛行是服從萊維分布的隨機搜索方法,在面對大范圍空間的優化問題上有著良好的表現[22]。其函數表達如公式(9)所示:
(9)
式中:ra和rb是[0,1]之間的隨機數,β是值為1.5的常量,σ計算如公式(10)所示:
(10)
式中:Γ(x)=(x-1)。
L3和L4中的粒子有著更好的空間搜索能力,利用萊維飛行對其中粒子優化,粒子更新方式如公式(11)所示:
(11)
2.2.3 層次學習隨機分形搜索算法
LLSFS算法步驟如下:
風影他們在東泉嶺承包了數十畝荒山,種植高山野茶,還養殖雞鴨牛羊。風影有一種稍縱即逝的、無可名狀的、不能用任何語言來表達的感覺,他已經無意去追尋虛無縹緲的夢幻與禪境,在時間的流程中,慢慢地在他的心底里沉淀下來,凝成一個化不開的內核,紅塵也許就是這個內核的外形。
步驟1:初始化粒子群P,計算每個粒子對應的函數適應度值F;
步驟2:進入迭代循環;
步驟3:粒子分形生成新粒子群Ptemp,計算粒子對應的函數適應度值Ftemp;
步驟4:根據Ftemp大小,對粒子群Ptemp進行排序,適應度值小的粒子保留;
步驟5:粒子群Ptemp分為4個層級,使用萊維飛行的層次學習策略生成新的粒子群Pnew,計算對應的函數適應度值Fnew;
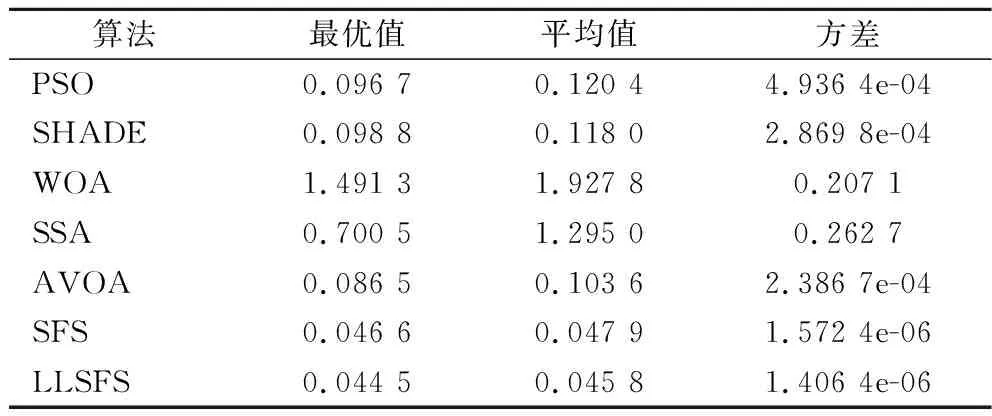
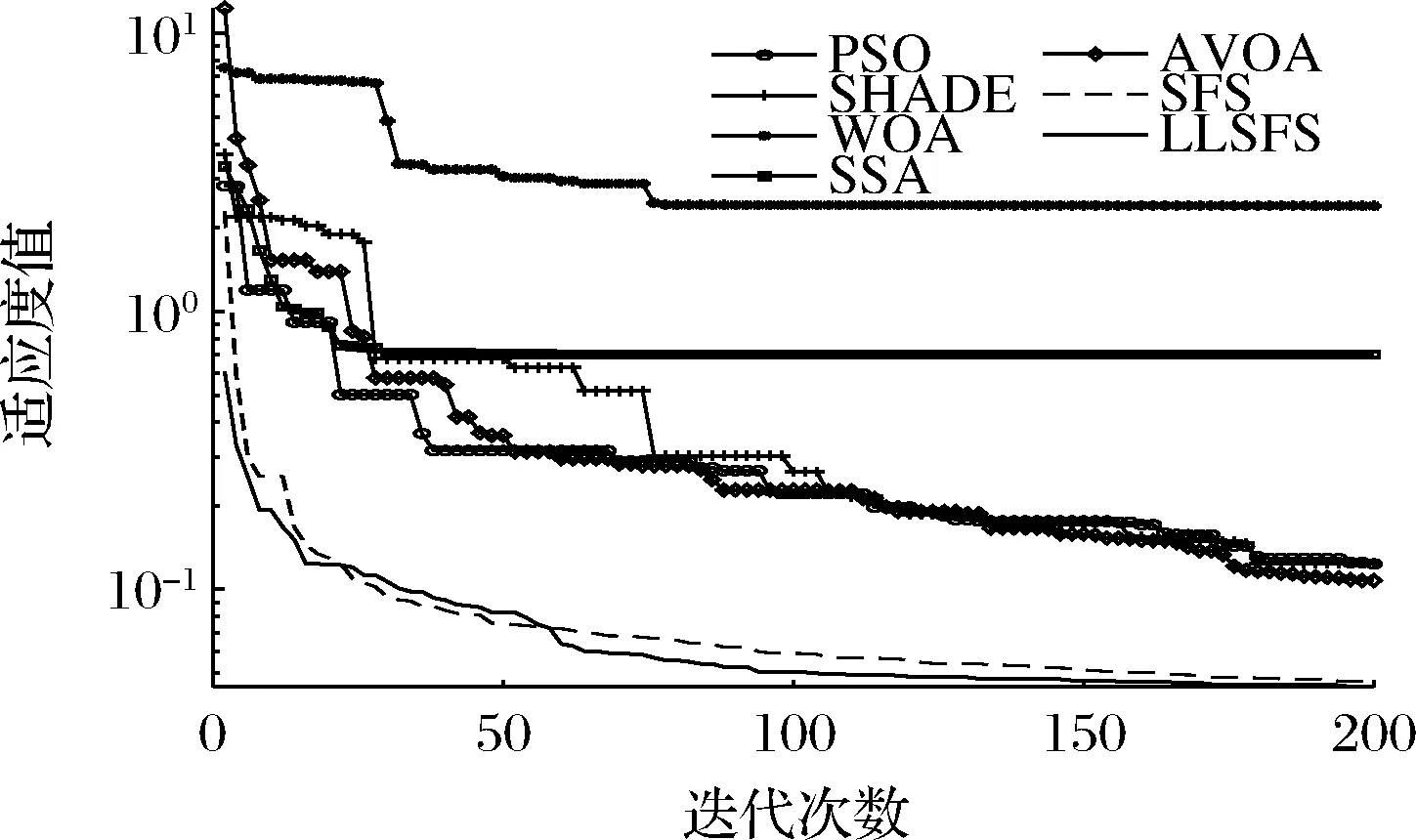
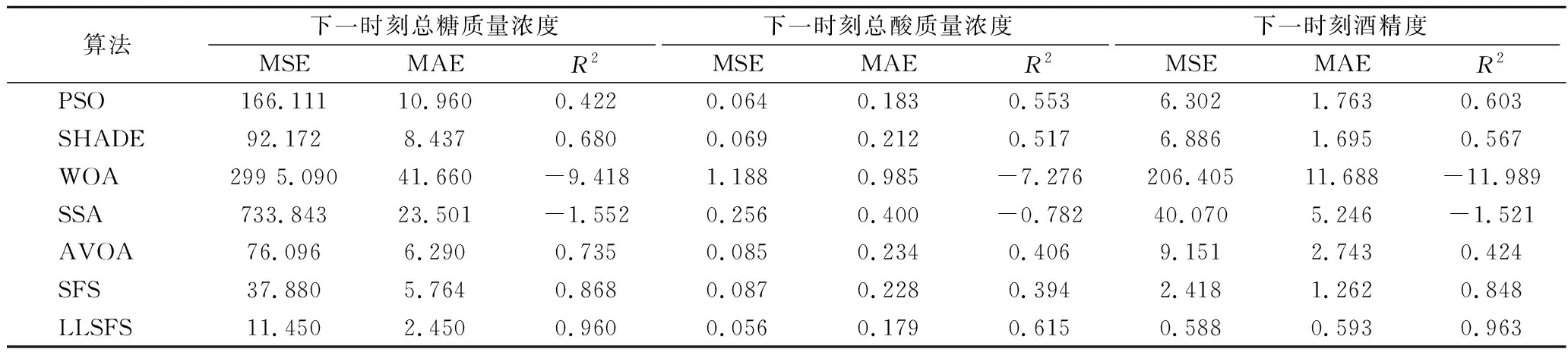
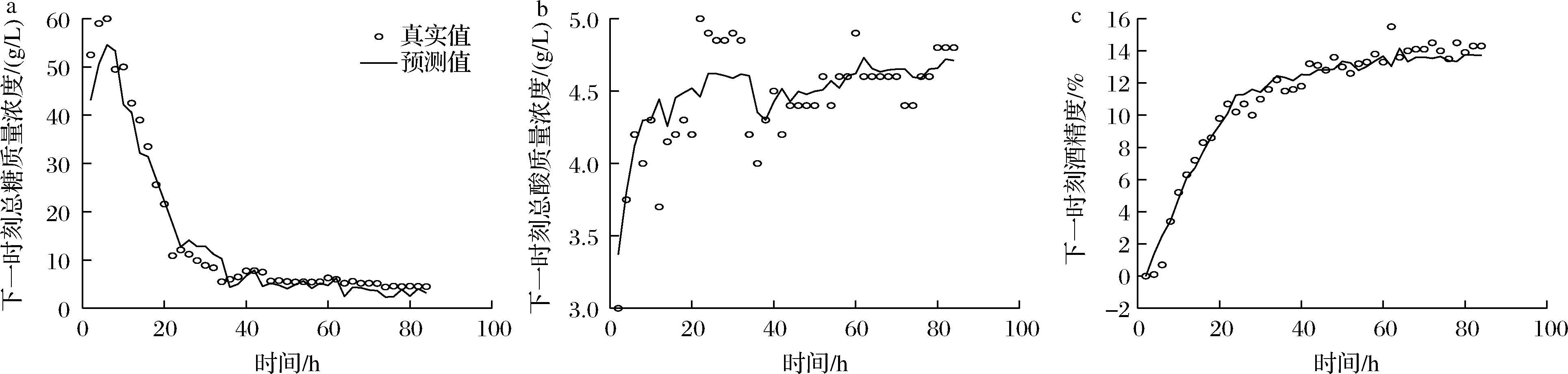
步驟6:如果Fnew 本文數據來自女兒紅酒廠黃酒前酵過程采集到的數據,5個生產批次共計212組數據樣本。4個發酵罐中170組數據作為訓練集,一個發酵罐中42組數據作為測試集。各維度數據之間差異大,故對數據進行了歸一化,取值范圍為[0,1]。輸入數據分別為:發酵過程的采樣時間(h)、溫度(T)、pH值、總糖質量濃度、總酸質量濃度、酒精度;輸出數據分別為:下一時刻的總糖質量濃度(h+2)、總酸質量濃度(h+2)、酒精度(h+2)。 本文采用的實驗平臺為:Window 10操作系統,主頻為2.9 GHz的Intel i5處理器,內存為8 GB,編程環境為MATLAB2020b。 本文分別采用PSO、SHADE[14]、WOA[17]、SSA、AVOA[19]、SFS與LLSFS進行實驗對比,對MOANFIS模型的參數進行尋優。LLSFS算法種群規模設置為48以保證層次學習中每層粒子數量相同,其余算法的種群規模為50。迭代次數為200次。 本文分別使用上述各算法對MOANFIS模型的適應度函數F獨立實驗10次。從實驗結果的最優值、平均值和方差3個維度評估各算法的性能。實驗結果表明,LLSFS算法在3個評價指標上均有著更好的表現。相比于SFS算法,LLSFS算法有著更快的收斂速度,全局搜索能力、魯棒性也得到進一步的提升。各算法的實驗結果如表1所示,圖4展示了各算法的收斂曲線。 表1 訓練集適應度值FTable 1 Fitness value F on training dataset 圖4 各算法對MOANFIS的收斂曲線Fig.4 Convergence curve of each algorithm to MOANFIS 模型的優劣主要取決了其在測試集上表現。本文分別從MSE、平均絕對值誤差(mean absolute error,MAE)、決定系數R23個評價指標考察MOANFIS模型的精度和泛化能力。首先將模型預測數據進行反歸一化還原為真實尺度的發酵數據,然后分別使用各評價指標進行分析。MSE的計算使用公式(7),MAE和R2的計算方式如公式(12)和公式(13)所示: (12) (13) 實驗結果表明,相比于其他算法,LLSFS-MOANFIS模型對下一時刻的總糖質量濃度、總酸質量濃度、酒精度均有著更準確地預測結果。從指標R2來看,LLSFS-MOANFIS模型的總糖質量濃度和酒精度的R2值分別為0.96和0.963,預測效果良好,但總酸濃度R2值為0.615,預測效果還有進一步提升的空間。實驗結果如表2所示。 表2 測試集實驗結果Table 2 Experimental results on testing dataset 本文將LLSFS-MOANFIS模型與基于發酵動力學的SSF[7]模型進行了對比。SSF模型分別針對3批黃酒發酵數據建立了不同模型,并未探討模型的泛化能力,但也有較好的參考價值。本文的測試集是和其論文中12罐的發酵數據是同一批數據,選用該批次數據進行實驗結果的對比分析。除了LLSFS-MOANFIS模型的總酸質量濃度R2表現不佳之外,其余各項指標中LLSFS-MOANFIS模型的擬合效果均優于SSF模型。結果如表3所示。 表3 SSF和LLSFS-MOANFIS的對比Table 3 Comparison of SSF and LLSFS-MOANFIS 圖5展示了LLSFS-MOANFIS模型在測試集上預測效果。從圖中可以看出,LLSFS-MOSNFIS對下一時刻總糖質量濃度、酒精度的擬合效果良好,但是對下一時刻總酸質量濃度的預測表現還有可提升的空間。一方面由于黃酒發酵過程中產生的有機酸是微量物質,不同批次之間的總酸質量濃度差異較大;另一方面,總酸質量濃度的數據分布較為分散,離群點較多,影響了擬合效果。 a-下一時刻總糖濃度預測;b-下一時刻總酸濃度;c-下一時刻酒精度預測圖5 LLSFS-MOANFIS在測試集上的實驗結果Fig.5 Experimental results of LLSFSOMOANFIS on testing dataset 本文針對黃酒發酵醪液中監控目標產物多樣的特點,提出了一種具有多輸出結構的MOANFIS模型,建立了當前時刻的發酵數據為輸入,下一時刻關鍵發酵數據為輸出的模型結構。同時本文提出的LLSFS算法對MOANFIS模型的參數進行了辨識優化,實驗結果表明LLSFS算法有著更好的全局搜索能力和魯棒性,提升了MOANFIS的精度。基于模糊系統理論的黃酒發酵建模研究工作為黃酒建模開辟了新的方向。3 結果與分析
3.1 黃酒發酵數據集
3.2 實驗設置
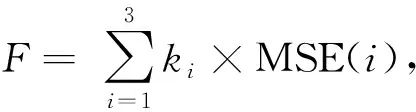
3.3 實驗結果及分析

4 結論

