基于動力學平均場的光晶格超冷原子量子模擬*

譚輝 曹睿 李永強2)?

1) (國防科技大學理學院,長沙 410073)

2) (國防科技大學,極端條件物理與應用湖南省重點實驗室,長沙 410073)

隨著原子冷卻技術與光晶格技術的發展,光晶格與超冷原子氣體組成的量子系統已經成為量子模擬中的有力工具.光晶格純凈和高度可控的性質賦予其強大的調控能力,如今,人們可以模擬更復雜和有趣的物理現象,從而加深對量子多體物理的認識.本文綜述了近年來本課題組利用玻色動力學平均場理論對強關聯區間的光晶格玻色體系進行的一系列研究,包括多組分玻色體系、高軌道玻色體系以及存在長程相互作用的體系等.通過玻色動力學平均場理論的計算,揭示了從弱相互作用區間到強相互作用區間出現的豐富物理現象,包括不同磁序的量子相、多步凝聚、超固體相以及高軌道體系中的自旋-角動量耦合和阻挫效應.

1 引言

量子模擬簡而言之就是利用其他可控的量子多體系統對真實復雜量子系統進行實驗或理論研究的一種方法[1].光晶格中的超冷原子氣體由于系統參數可控和成熟的實驗技術,已經成為了一個完善的量子模擬實驗平臺[2,3].光晶格通常是由相干激光束形成的,通過控制激光的數目和角度來實現不同維度[4-6]和不同結構[7-11]的周期性晶格結構,從而模擬固體中的晶格.在光晶格中,人們可以自由調節晶格深度[6],可以研究晶格無序性,還可以設計出有等效磁場的系統,其磁場強度可以達到目前固體物理實驗室中最大磁場的數百倍[12].除此之外,人們可以精確控制激光的相對相位,實現可編程的連續可調晶格系統,這些實驗技術大大拓展了光晶格的調控和模擬能力[13,14].中性原子在激光的交變電場中被極化,從而受到偶極力被陷俘在這樣的周期性光晶格中[15].根據激光波長的不同,光晶格中的原子被陷俘在波結或波腹,這種相干激光束產生的周期性晶格勢會產生一系列布洛赫能帶.一般而言,原子在轉移到光學晶格之前就被冷卻到了足夠低的溫度,因此在絕熱地裝載在光晶格后只有最低的布洛赫帶被填充,當晶格勢足夠深時,該體系可以用一個簡單的單能帶緊束縛模型描述[16],該模型主要包含原子在格點上的相互作用以及在格點間的躍遷振幅,通過調節晶格深度或者通過費什巴赫(Feshbach)共振[17-19]改變躍遷振幅與原子間相互作用的比值大小可以觀察到豐富的量子相.

1995 年,玻色-愛因斯坦凝聚首次在實驗中被觀察到[20,21],六年后Greiner 研究組[6]成功將原子裝載在光晶格中并觀察到了著名的莫特絕緣相,莫特絕緣相是一個典型的強關聯相,由于原子間的相互作用非常強,原子局域在各個格點上,每個格點上的粒子數都是整數.這一想法最開始來自Jaksch和他的同事[22],他們提出光晶格中的原子可以模擬固體材料中的電子行為,并模擬哈伯德模型.在Greiner 等的實驗之后,利用光晶格中的超冷原子進行量子模擬的實驗和理論研究如雨后春筍般大量涌現.基于光晶格中超冷原子的量子模擬也成為了現代物理中不可或缺的一部分[23-31].

隨著實驗技術的發展,人們開始對自旋玻色體系進行研究[32],這里的自旋可以是原子不同的超精細態,也可以是不同種類的原子.在這樣的體系中,自旋關聯起著重要作用,并且會帶來不同于標量玻色子體系的物理現象.在最近的實驗中,旋量超冷玻色體系已經被實現了[33-37],并出現了非常廣泛的研究,如自旋混合[38,39]、自旋波[40,41]、自旋動力學[42-46]、自旋圖案[47-49]以及相變[50-52].這些實驗為研究自旋關聯凝聚體中的量子現象提供了新的路徑,也激起了對光晶格中旋量玻色氣體的進一步研究[53-58].此外,研究表明: 在外加磁場下,體系基態的簡并被打破,自旋相互作用與原子間短程相互作用的競爭會引起豐富的強關聯量子相[31,32,59,60].

除了原子間的短程相互作用,長程相互作用也是強關聯體系中的一個重要組成部分,具有長程相互作用的體系傾向于形成新的量子相[61].長程相互作用通常出現在材料科學中,并與短程相互作用競爭導致空間調制相的出現[62].在光晶格超冷原子體系中有兩種方式可以帶來長程相互作用: 一是利用超冷原子間的偶極力[61];二是將原子與高精細腔耦合,腔場自洽地將所有原子耦合在一起,可以等效地認為原子間具有長程相互作用[63-66].偶極玻色-愛因斯坦凝聚體[67]、極性分子[68]和耦合到光學腔[63,69]的玻色-愛因斯坦凝聚體的實驗實現,為具有長程相互作用的量子氣體的研究開辟了新的道路,也為研究具有新奇性質的量子相提供了更多的途徑.

此外,軌道自由度也是量子材料中重要的組成部分,其與自旋自由度、電荷自由度等一起構成了量子材料的物理特性.對于軌道自由度的研究,極大地豐富了人們對于基礎物理機制的認知.在冷原子量子模擬中,這種高軌道原子系統具有的空間各向異性,帶來了豐富的物理現象[70-79].在實驗方面,隨著技術的不斷提高,高軌道冷原子的相關實驗也取得了豐碩的成果.最早在實驗室觀測到p 能帶現象是2007 年由Bloch 研究組[80]實現的,之后漢堡大學的Hemmerich 小組[81,82]利用二分晶格(bipartite lattice)實現了正方晶格的p 軌道玻色凝聚,并觀測到p 能帶玻色系統中存在px+ipy的手征超流.近年來,隨著實驗技術的不斷提高,三角晶格、六角晶格的p 軌道玻色系統和高軌道費米系統[83,84]也已經被實現,并觀察到了非常有趣的物理現象[75,85-89].

總的來說,光晶格中的超冷原子為量子多體問題的模擬提供了理想的平臺,在凝聚態物理、統計物理、量子化學、高能量物理等領域中都起著重要作用[90].第2 部分詳細介紹玻色動力學平均場理論,該理論對于研究高維強關聯體系是非常有效的.第3,4,5 部分分別介紹了我們近幾年在旋量玻色體系、存在長程相互作用體系、高軌道玻色體系的研究.最后是總結和展望.

2 玻色動力學平均場理論

在多體系統中,由于粒子間復雜的相互作用,整個體系是密切關聯在一起的,因此理論求解是非常困難的.要處理多體系統,只能采取近似處理、數值求解的方法.目前研究多體系統的方法有平均場理論、密度矩陣重整化群、量子蒙特卡羅方法、動力學平均場理論(dynamical mean-field theory,DMFT)、精確對角化等.本文主要介紹玻色動力學平均場理論(Bosonic dynamical mean-field theory,BDMFT).

動力學平均場理論的研究始于1989 年,Vollhardt 和Metzner[91]研究發現無窮維度下Fermion-Hubbard 模型可以進行簡化.同年,Hartmann[92,93]指出在無窮維下關聯將變得局域,動量將不再重要,這種局域的關聯具有動力學屬性,任何非局域的關聯效應都可以用一個靜態的平均場描述.之后,1991 年,Jani?[94]利用動力學干涉勢近似理論給出了無窮維下Hubbard 模型的格林函數和自能的泛函方程.在此基礎上,Georges 與Kotliar[95]利用Anderson 雜質模型將DMFT 的自洽方程推廣到了Hubbard 模型,DMFT 的基本框架構建完成.從1989 年開始,到1991 年結束,短短三年的時間,動力學平均場理論就建立完成,動力學平均場理論被廣泛地用于材料計算、多體系統等,拓展了數值求解物理問題的計算方法,是處理多體問題的一種高效的計算手段.

動力學平均場的核心思想是無窮維極限下系統的局域性.在無窮維度下,自能是嚴格局域的,系統的空間漲落被凍結,只剩下了局域的量子漲落,此時就可以將多體系統解耦成單體問題,因此動力學平均場理論是一種考慮了局部量子漲落的數值方法,如圖1[96]所示.在無窮維度下自能是嚴格局域的,因此動力學平均場理論對于低維度問題的計算誤差比較大,但隨著研究發現,二維、三維的多體系統中動力學平均場理論的結果也令人滿意[97-99].因此,動力學平均場理論是計算二維及以上維度強關聯、弱耦合區間的一個主要方法.

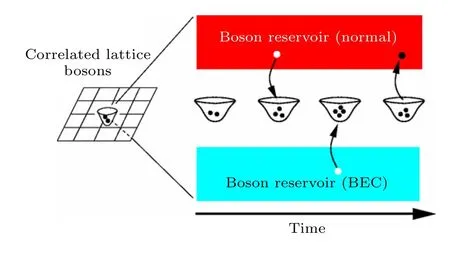
圖1 玻色動力學平均場示意圖.通過與普通玻色子熱庫和玻色-愛因斯坦凝聚熱庫耦合[96],多體格點問題退化為一個單格點問題Fig.1.Schematic picture of BDMFT.In BDMFT,the many-body lattice problem is reduced to a single lattice problem coupling with normal Bosonic reservoir and reservoir of Bose-Einstein condensate (BEC)[96].

考慮一個一般的Bose-Hubbard 模型,其哈密頓量可寫為

式中,τ=it′是根據時間t′定義的虛時;H(τ) 為虛時下的體系哈密頓量;β=1/(kBT) ,其中kB為玻爾茲曼常數,T為體系的溫度.可以將作用量分成3 個部分S0,?S和S(0),其中,S0是只有格點i=0的有效作用量,即

?S是僅包含了i=0 格點與其周圍格點的躍遷過程的作用量,

(13)式中引入了Weiss 格林函數,有

其中,σz是泡利矩陣.由于考慮的是高維情況,為了使得此時動能不發散,需要對躍遷項做變換是配位數[96,97,102].其原因是在計算最近鄰躍遷的過程中,會多出一個配位數z,因此在無窮維度下,會出現動能發散的情況,故需要在此處進行一個修正.上面的這種將雜質格點從整個多體系統中解耦出來,變成一個雜質格點與熱浴耦合的方法,被稱為“空腔方法”[96,97,103].

在松原頻率的表象下,Weiss 格林函數可寫成

其中,ωn=2πn/β是松原頻率.Weiss 格林函數滿足Dyson 方程:

式中,Σimp是雜質格點的自能;雜質格點的格林函數滿足

其中,εk是色散關系.在這里,近似認為自能是個局域的量,即Σ(k,iωn)≈Σimp(iωn) .這個近似在系統處于無窮維度時是嚴格成立的,在高維下基本符合.但這種近似無法處理由空間關聯所帶來的物理現象,對于長程相互作用、自旋液體等物理問題無法得到很好的結果.現在,互相包含了對方,DMFT 的自洽回路已形成.給Weiss格林函數一個試探值,就可以求解作用量(13)式,之后就可求出自能Σimp等物理量,利用Dyson 方程(16),可以得到新的,構成一個自洽回路.

在上面的自洽過程中,求解作用量是非常困難的,因此比較好的方法是將作用量映射到可以求解的模型上.這個可解的模型要能夠較為完美地描述雜質格點與環境的物理狀態,對于雜質格點不僅要考慮到單格點,還需要考慮到其和環境的關聯,Georges 和Kotliar[95]提出Anderson 雜質模型的映射方法是現在DMFT 廣泛使用的方法.Anderson雜質模型哈密頓量可寫為[103,104]

(18)式中,相互作用部分和化學勢直接從Hubbard 模型中得到.玻色-愛因斯坦凝聚的玻色子熱庫由超流序參量?ν描述,普通玻色子的熱庫由一定數目的軌道表示,其中和εl為軌道的產生算符和能量.雜質格點通過正常躍遷振幅Vν,l和反常躍遷振幅Wν,l與軌道耦合起來,因此{εl,Vl,Wl}也被稱為Anderson 參數.哈密頓量(18)的作用量分別有雜質部分作用量

因此,可以得到Weiss 格林函數新的表達方式如下:

對于Anderson 雜質模型,可以利用數值的方式求解這個單體哈密頓量.在動力學平均場方法中,這種求解Anderson 雜質模型所用不同的數值手段就叫做雜質求解器.常用的雜質求解器有精確對角化[105,106]、量子蒙特卡羅方法[107]、數值重整化群[108]等.對應于不同的物理系統,雜質求解器的選取非常重要.通過雜質求解器求解Anderson 雜質模型,就可以得到哈密頓量的本征態和本征能量,以及超流序參量等物理量.在Lehmann 表象下,可以用本征態和本征能量表示局域格林函數

其中,|m〉為本征態,Em為對應的能量.因此,系統的自能可以寫成

此處,考慮了自能近似,即認為自能是局域的,因此滿足Σimp(iwn)≈Σlat(iwn) .由Dyson 方程(16),能夠得到格點格林函數為

現在,利用Anderson 雜質模型構造的動力學平均場方法的自洽循環便完成了.利用Anderson雜質模型,成功繞開求解作用量來實現動力學平均場的自洽過程.在Anderson 雜質模型中,動力學平均場的循環為: 先給出Anderson 參數的試探值,利用雜質求解器求解Anderson 雜質模型哈密頓量,便能夠得到系統的本征態和本征能量,進一步可以求得自能、超流序參量等物理量,然后利用(28)式求得新的格點格林函數.利用新求得的格點格林函數,可以得到新的Anderson 參量,然后再重新循環上述過程,直到滿足自洽條件,輸出最終所求系統的物理量,如圖2 所示.

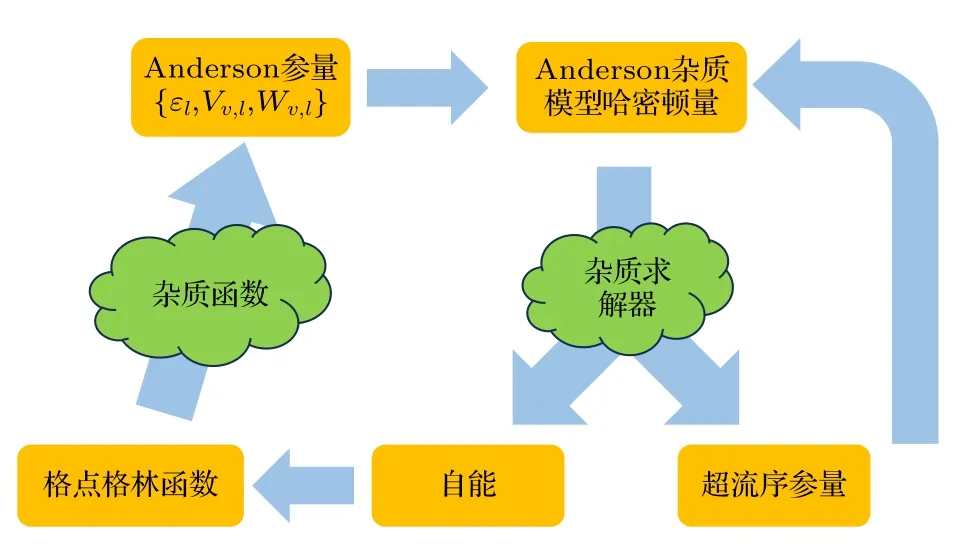
圖2 Anderson 雜質模型下動力學平均場方法的自洽循環示意圖.給Anderson 參數初值,利用雜質求解器求解Anderson 雜質模型,得到物理量和自能,通過自能得到格點格林函數,利用Dyson 方程得到雜質函數,從而得到新的Anderson 參量,構成自洽過程Fig.2.Schematic picture of BDMFT loop in Anderson impurity model.For an initial value of Anderson parameters,physical quantities and self-energy are obtained by solving the Anderson impurity model.After obtain lattice Green function through self-energy,impurity functions are attained.Finally,the loop is complete by fetched new Anderson parameters from impurity functions.

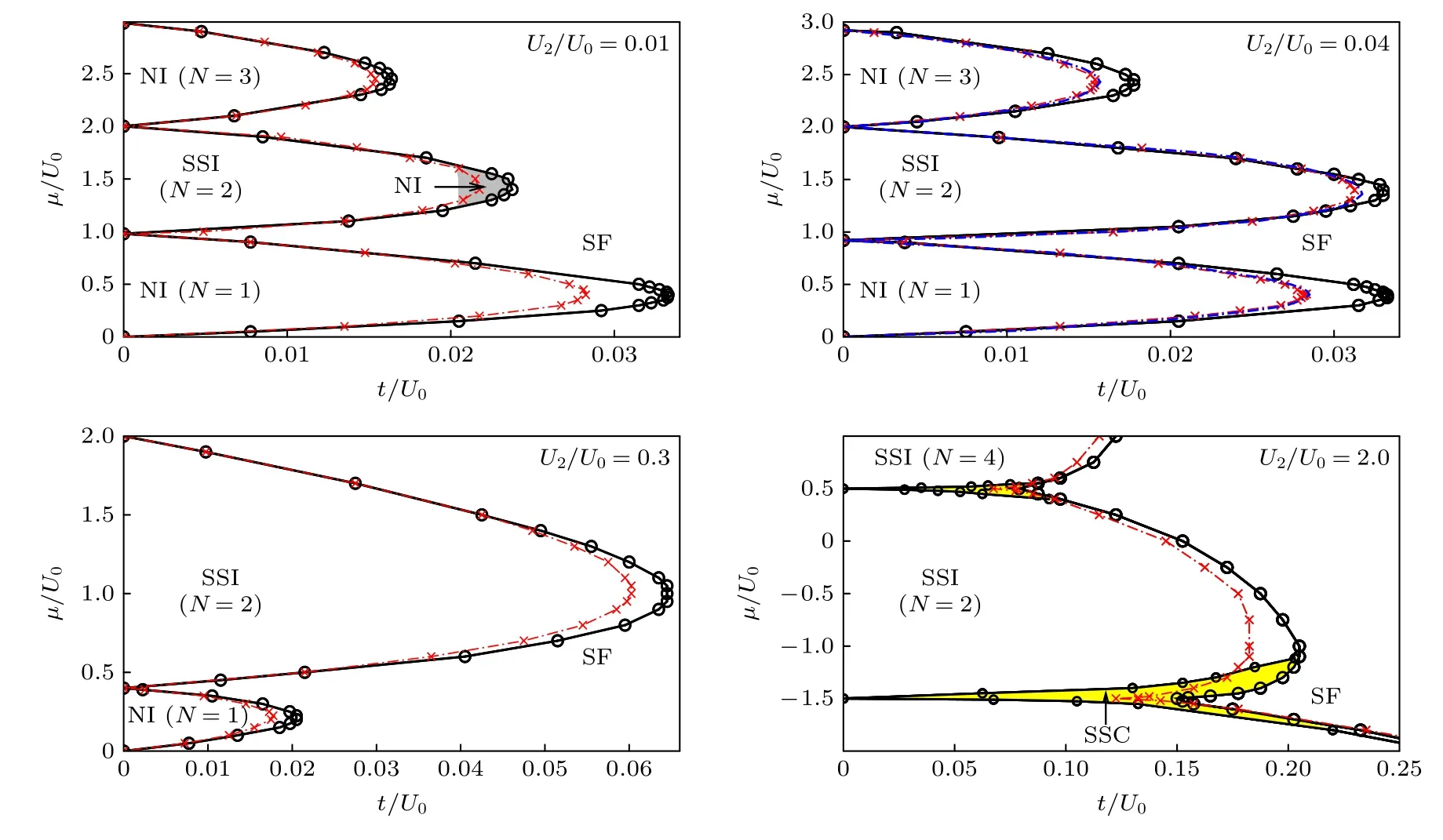
圖3 三維光晶格中自旋-1 超冷玻色子在不同反鐵磁相互作用下的零溫相圖[119],U2/U0分別為0.01,0.04 (23Na),0.3,和2.0.數據來源于BDMFT(黑線),Gutwiller(紅線)以及文獻[117](藍線)中的計算.體系中存在4 種不同的相,即超流相(SF)、向列絕緣相(NI)、自旋單態絕緣相(SSI)和自旋單態凝聚相(SSC)Fig.3.Zero-temperature phase diagram for spin-1 ultracold bosons in a 3D cubic lattice[119] for different antiferromagnetic interactions U2/U0=0.01,0.04 (23Na),0.3,and 2.0,respectively,obtained via BDMFT (black circle),Gutzwiller (red cross) and in Ref.[117](blue dashed).There are four different phases in these diagrams: superfluid (SF),nematic insulator (NI),spin-singlet insulator (SSI)and spin-singlet condensate (SSC).

雖然用Anderson 雜質模型可以很好地求解動力學平均場,但在真實的實驗中,由于外場或人工規范場,冷原子系統并不是各向同性的.因此,需要對現在的動力學平均場理論進行進一步拓展.類似于費米系統的實空間動力學平均場理論[109,110],我們發展了實空間玻色動力學平均場理論(RBDMFT).在實空間玻色子動力學平均場理論中,雖然自能是局域的,但各個空間位置的自能是不同的,即.因此,利用實空間動力學平均場理論,可以求解各向異性的Hubbard 模型,并得到較好的結果.

3 光晶格中多組分玻色子體系的磁性研究

3.1 三維光晶格中自旋-1 超冷玻色氣體的磁性相變研究

隨著超冷原子氣體在光晶格中的實現,理論研究也變得非常廣泛,量子蒙特卡羅方法和密度重整化群理論可以在一維情形下進行研究[53-56],而在三維體系中,對強關聯量子相的研究一般都是通過晶格規范理論預測[111],強耦合極限下的有效自旋模型[112,113]以及靜態平均場理論[114-118]等方法.而超越了靜態平均場理論,從弱耦合到強耦合極限下的量子多體相圖還幾乎沒有人研究.因此本課題組利用玻色動力學平均場理論研究了自旋-1 玻色體系中的量子相變[119].在適當的晶格深度下,自旋-1的玻色子體系可以用緊束縛近似下的玻色-哈伯德模型描述:

進一步地,研究了溫度對體系的影響,并觀察到超流體可以通過一階(二階)相變被加熱成具有偶(奇)填充的莫特絕緣體,類似于3He 中的Pomeranchuk 效應.我們發現有序態(如向列絕緣相和自旋單態絕緣相)的臨界溫度在現有的冷卻方案范圍內,這表明有機會使用現有的實驗技術直接觀察這些相.

3.2 三維光晶格中磁場下自旋-1 超冷玻色氣體的相變研究

研究多組分超冷原子氣體的磁序和玻色-愛因斯坦凝聚體之間的聯系是一個有趣的話題.對于旋量氣體,理論上已經預測了多步凝聚[120-125],并在實驗中被觀察到了[50,126,127].例如,對于較小的塞曼場,反鐵磁相互作用定性地改變了相圖并導致在超精細態mF=±1 態下的凝聚[128],然而對光晶格中自旋玻色氣體的多步凝聚目前還沒有人進行研究.因此緊接著上面的工作,本課題組基于玻色動力學平均場理論,系統地研究了該自旋-1 玻色子體系在存在外部塞曼相互作用時的性質[129].體系的哈密頓量與無磁場的自旋-1 玻色子體系相比,多了線性塞曼能量p和二次塞曼能量q這兩項:

這是由于外加磁場導致超精細態(mF=1,0,-1)退簡并的塞曼效應,其中p=(E-1-E1)/2 ,q=(E1+E-1-2E0)/2,U0為原子間的相互作用,U2為自旋相互作用.在這一體系中,塞曼相互作用與自旋相互作用的競爭會出現非常多有趣的相.對于反鐵磁自旋相互作用,以23Na (U2/U0≈0.037[52])為例,計算該體系的多體相圖,體系存在向列絕緣相、鐵磁相、自旋單態絕緣相和不同類型的超流相.計算表明二次塞曼項使得粒子數為偶數的區域出現了向列絕緣相,在塞曼能量非常大時,體系的莫特絕緣區完全處于向列莫特絕緣相.對于鐵磁自旋相互作用的情況,以7Li(U2/U0≈-0.7[112])和87Rb(U2/U0≈-0.005[20])為例,繪制了鐵磁和向列絕緣相、超流體相等相圖,計算結果表明隨著塞曼能量的增強,鐵磁絕緣相的區域逐漸由向列絕緣相取代.此外,我們還研究了這些量子相對熱漲落的穩定性,得到了有限溫度下的相圖.

同時,對超流體的分步凝聚進行了研究,給出了各個塞曼組分的臨界凝聚溫度Tc與縱向磁化強度的關系.有趣的是,在反鐵磁相互作用下我們觀察到了超精細態mF=-1 組分的臨界溫度隨著縱向磁化強度的非連續變化: 隨著縱向磁化強度的增加,臨界溫度首先降低至0,然后逐漸增長到某一最大值后再逐漸降為0;而對于鐵磁相互作用,超精細態mF=0 的臨界凝聚溫度Tc會首先減小到某一極小值點,然后增長到某一極大值,最后減小到0.這反映了強關聯超冷玻色氣體的獨特性質.

3.3 自旋堿金屬與堿土金屬混合體系的磁性研究

量子磁性在固態系統中起著重要作用,揭示量子多體系統磁序背后的機制一直是理論研究和實驗研究的熱點.最近,超冷旋量玻色子的異核混合物已經在實驗上被實現,如旋量堿金屬原子的異核混合物[130]、旋量堿金屬和堿土金屬原子的混合物[131,132],然而在光晶格中還沒有對旋量堿金屬和堿土金屬原子混合體系的研究.在3.1 節和3.2 節中研究了自旋-1 玻色子體系的基態相圖,以及該體系存在磁場時的性質.本節主要研究三維光晶格中自旋-1 堿金屬原子與自旋-0 堿土金屬原子混合體系的基態相圖[133].體系的哈密頓量由緊束縛近似下的玻色-哈伯德模型描述:

首先研究種間相互作用U12對相圖的影響.對于較小的種間相互作用,兩種原子是互相混合的.但是對于較大的種間相互作用,體系會出現相分離.當種間相互作用減小時,n=1 的區域會減小,而n=2 的區域會增大.這是因為在U12?U1,2的條件下,n=2 的區域更容易形成自旋單重態.對于較大的種間相互作用U12/U1=2,我們觀察到體系出現了相分離.這里只得到了自旋-187Rb 原子的相圖.作為比較,也用Gutzwiller 平均場理論計算了自旋-1 和自旋-0混合體系的基態相圖,如圖4[133]中的紅線所示.Gutzwiller 的計算結果是小于BDMFT 的計算結果的,這正是由于BDMFT 包含了量子漲落.

為了更好地描述87Rb 和84Sr 的混合體系,我們把87Rb 當作自旋↓,把84Sr 當作自旋↓.計算表明,系統在填充數n≡nRb+nSr=1 (nRb=nSr=0.5)時具有非零的磁性,Mtot≠0 ,而在填充數n=2時磁性為零,Mtot=0 ,這里nSr(nRb) 表示84Sr87Rb在格點上的填充數.也就是說整個體系在格點上粒子數為1 時處于鐵磁絕緣相,在粒子填充數為2 時處于無序絕緣相.這其中的物理規律可以通過在強相互作用下推導的玻色-玻色混合體系的有效自旋模型來理解.當格點上粒子填充數為1 時,由于幾乎相同的隧穿振幅,鐵磁自旋耦合占據主導,因此體系表現為鐵磁序.而當格點上粒子數為2時,由于種間相互作用U12?U1,2,自旋漲落被抑制,于是體系表現為無序絕緣相.在遠離莫特絕緣區時,隨著隧穿振幅的增大,密度漲落成為主導,系統經歷量子相變進入超流相.并且由于質量的不平衡,質量較大的 Rb 會先解除局域化( MISr+SFRb),之 后隨著隧穿振幅的繼續增大,兩種原子都會處于非局域化的狀態(2SF).

此外還研究了在三維光晶格中具有反鐵磁相互作用的23Na和84Sr 原子的混合體系.對于23Na 和84Sr 原子的混合體系,在填充數為1 的區域是鐵磁相(FM),在填充數為2 的區域是無序相(UI).有趣的是自旋-123Na 原子在填充數為1 和2 的情形都展示了從向列絕緣相到極化超流相的相變,這與單獨將23Na 原子放在光晶格中偶數填充的情形是不一樣的.

4 具有長程相互作用的光晶格體系的研究

4.1 偶極玻色氣體中的超固態相研究

為了實現由兩體相互作用誘導的超固體相(supersolid,SS),人們在極性分子[68,134-140]、磁性[16,67,141]和里德伯原子[142-150]上付出了巨大的努力,然而理論上提出的方案通常在實驗上都難以實現.本課題組提出一種可行的方案,研究了二維光晶格中雙組分玻色混合體系的超固態相[151],其中一個組分通過非共振激光被耦合到了里德伯態,因此在這一組分之間存在長程相互作用,如圖5[151]所示.

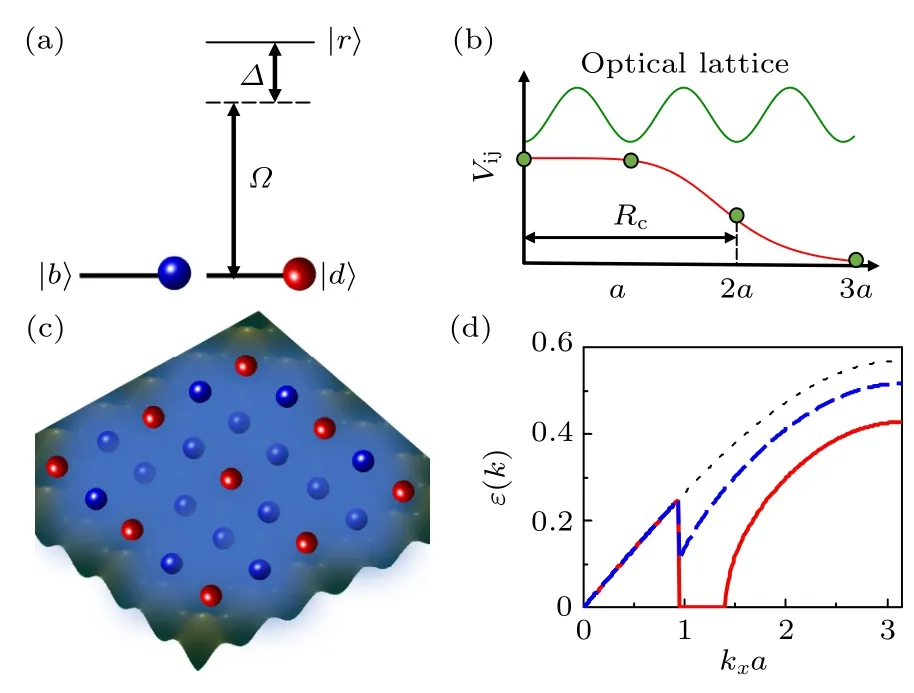
圖5 (a)考慮兩個電子基態 |b〉 (藍色),|d〉 (紅色)和一個里德伯態 |r〉 .一束非共振激光(拉比頻率為Ω,失諧量為Δ)將態 |d〉 與 |r〉 耦合.(b)里德伯態 |d〉 間的軟核型相互作用勢 Vij (紅線).軟核 半徑 Rc 可以大于 晶格 間距a,圖中展 示的是 Rc=2a 的情形.(c)被修飾原子處于有序密度波(DW)時的裸態處于SS.(d)裸態的Roton 不穩定性.聲子的Bogoliubov 色散關系(沿 kx 軸)被種間相互作用顯著地改變.當種間相互作用 Ubd 增 加時,會 出現類Roton 不穩定性,表明基態相由均勻的超流體轉變為超固體.圖中Ubd/U=0 (點線),Ubd/U=0.45 (虛線),Ubd/U=1 (實線),其他參數 為 ky=0,V/U=0.4 ,和 t/U=0.04 [151]Fig.5.(a) Two electronic ground states |b〉 (blue) and|d〉(red) and a Rydberg state |r〉 are considered.An off-resonant laser (with Rabi frequency Ω and detuning Δ) weakly couples the state |d〉 to |r〉 .(b) The soft-core shape interaction potential Vij (red) between atoms in the Rydberg dressed state |d〉 .The soft-core radius Rc can be larger than the lattice spacing a.Here,Rc=2a is shown.(c) SS of the bare state when dressed atoms are in an ordered density wave (DW).(d) Roton instability of the bare species.The Bogoliubov dispersion relation (along the kx axis) of phonons is significantly modified by the interspecies interaction.A rotonlike instability emerges when the interspecies interaction Ubd is increased,indicating that the groundstate phase changes from a homogeneous superfluid to supersolid.We show Ubd/U=0 (dotted line),Ubd/U=0.45 (dashed line),and Ubd/U=1 (solid line).Other parameters are ky=0,V/U=0.4 ,and t/U=0.04 [151].

在適當深的光晶格中,體系由一個單帶雙組分哈伯德模型描述:這里算符下標σ=d表示處于里德伯態的原子,下標σ=b表示另一組分的原子,tσ表示σ組分原子的躍遷振幅,Vij表示不同格點間原子的相互作用,Uσσ′為同一格點上同種或不同種原子間的相互作用.

基于實空間玻色動力學平均場理論,計算了該體系的完整相圖.在強耦合極限下(即原子間的短程相互作用遠大于動能)體系傾向于形成莫特絕緣相或密度波相(density wave phase).有趣的是我們發現了一個原子總密度分布不均勻的密度波相(ni,b=1,ni,d=2),它打破了晶格平移對稱性.在遠離莫特區的地方,如中間區域,觀察到兩種從莫特絕緣相到超固體相的量子相變,即未耦合的基態從莫特絕緣態到裸態形成的超固體(SS1)的相變,而被修飾的原子仍然處于莫特絕緣態.進一步增加隧穿振幅t,兩種原子都進入了超固體相(SS2).有趣的是,在模擬中觀察到一個明顯的超固體區域,這是兩種原子間相互作用的結果,表明與單組分情況[152]相比,在現實實驗中直接觀察到這些相變過程的概率更高.事實上,還觀察到SS1 和SS2 的寬度隨種間相互作用的減小而縮小,對于較小的種間相互作用Ubd,SS1 相消失了.此外還發現,雖然裸態原子只具有短程相互作用,但是另外一種原子間的長程相互作用依舊移動了MI 和SS1 之間的相變.

最后在t?Uσσ′的弱相互作用區間,體系形成原子總密度分布均勻的超流態,并且兩種原子的密度分布也是均勻的.這是由于劇烈的密度漲落破壞了晶體序,因此體系只能形成密度分布均勻的超流態.

4.2 光腔中的超輻射相研究

2010 年,Baumann 等[63]實現了玻色-愛因斯坦凝聚體與光腔耦合的開放系統中的Dicke 量子相變,并觀察到了自組織相的出現.該相變是由凝聚體原子之間的無限長程相互作用驅動的,由涉及腔模和泵浦光場的雙光子過程引起.簡單來說,均勻原子密度中的量子漲落使得所應用的橫向駐波激光中的光子被集體散射到腔模中.反過來,散射到腔中的光子又非線性地作用于原子,并放大了BEC 密度的漲落.當泵浦光功率小于臨界泵浦光功率時,腔模中的光子數為0,原子凝聚在低動量態上.在橫向激光的臨界泵浦功率以上,低動量態的原子被散射到高動量態,系統經歷可逆的零溫量子相變成為完美和有序的晶體.近年來在這一領域出現了非常多的研究,包括對多模光腔[153-155]、極限環[156]、時間晶體[157]、拓撲相變[158]以及對非厄米趨膚效應[159]的研究.理論上,通過改變激光頻率與腔共振的關系,可以將腔誘導的原子間相互作用從吸引調到排斥,在藍失諧驅動的高精細腔中也出現了非常多有趣的研究,如對Su-Schrieffer-Heeger 模型[160]、時間晶體[161-164]、p-軌道自組織相[165]以及結構相變的研究[166].

本課題組研究了超冷玻色氣體與藍失諧激光驅動的高精細腔的耦合體系,探索該體系在弱相互作用與強相互作用區間可能出現的量子相[167].實驗裝置如圖6[167]所示.

圖6 原子在光腔中耦合高軌道態示意圖[167] (a)原子被陷俘在光腔中,由一束不平衡因子 η=E-/E+ 的橫向泵浦光驅動;(b)四方晶格的布里淵區示意圖,原子從動量態k=(0,0) 被散射到 (π,π),右側上下兩幅圖分別為p-軌道和d-軌道能帶原子的動量分布圖;(c),(d)腔模和泵浦光之間的主要散射過程,其引起了高軌道激發.通過控制參數η=1(c),原子可以選擇性地被散射到偶宇稱的d-軌道態,當η <1 (d),原子被散射到奇宇稱的p-軌道態.此處 ,和 分別表示s-軌道和dxy -軌道,px -軌道和 py -軌道,s-軌道和 px -軌道,py -軌道和 dxy -軌道在格點i 和格點j 間由散射引起的軌道反轉躍遷Fig.6.Populating higher-orbital states with ultracold atoms in an optical cavity[167]: (a) Atoms are prepared in an opticalcavity,pumped by a blue-detuned laser in the transverse direction with an imbalance parameter η=E-/E+ .(b) Brillouin zone of the square lattice,where atoms are scattered from the quasimomentum state k=(0,0) to the excite state (π,π),with quasimomentum distributions for the p-and d-orbital bands shown in right upper and lower panels,respectively;(c),(d) dominating scattering processes of atoms induced by cavity,leading to higher-orbital excitations.By controlling η,atoms can be selectively scattered into the even-parity dxy -orbital state with a single node in both x and y directions for η=1 (c),or into the odd-parity p-orbital state with a single node only in one direction for η <1 (d).Here, ,anddenote cavity induced orbital-flip hoppings between sites i and j for the s-and dxy -orbitals,px -and py -orbitals,s-and px -orbitals,and py -and dxy -orbitals,respectively.

87Rb 原子被裝載在耗散κ=40ωr的高精細單模光腔中,ωr是反沖頻率.原子由垂直于腔模方向,即y方向的兩束對向傳播的波長為 780.1 nm 的藍失諧激光驅動,這可以通過一束激光和反射鏡實現.這兩束對向傳播激光強度的不平衡由鏡子的反射率控制η≡E-/E+,這里E+和E-分別為入射光和反射光的振幅.在第3 個方向,也就是z方向,用一束非常強的激光來凍結原子的運動自由度.體系由下面的玻色-哈伯德模型描述:

通常來說在光腔系統中,主要過程為泵浦光和腔模通過原子而發生的散射過程,散射項的宇稱和系統的維度起著重要作用.在紅失諧光的條件下,由于散射項是偶宇稱的,原子處在s-軌道.然而在藍失諧體系中,由于散射項為奇宇稱,原子可以從s-軌道散射到更高的軌道.在我們考慮的二維藍失諧體系中,原子可以被散射到奇宇稱的p-軌道和偶宇稱的d-軌道,形成穩定的強關聯高軌道相.如圖6(c)[167]所示,由于在x和y方向都是奇宇稱的,因此它會改變軌道在x和y方向的宇稱,從而將原子從s-軌道散射到d-軌道以及從 px-軌道散射到 py-軌道.如圖6(d)[167]所示,V?2在x方向是奇宇稱,在y方向是偶宇稱,因此它只改變軌道在x方向的宇稱,從而將原子從s-軌道散射到 px-軌道以及從 py-軌道散射到d-軌道.有趣的是,與紅失諧泵浦光體系超輻射相伴隨著電荷-密度波的出現不同,在藍失諧的腔中,由于散射導致的軌道-翻轉隧穿,自組織相的形成伴隨著軌道-密度波的出現.

總的來說我們發現在二維光晶格中,通過改變泵浦光的反射率,原子可以被散射到偶宇稱的d-軌道能帶和奇宇稱的p-軌道能帶,形成穩定的高軌道自組織超流相和莫特-絕緣相,這提供了一種新的調控高軌道現象的機制.

5 光晶格中的高軌道玻色子體系研究

5.1 旋轉對稱性增強的p 軌道玻色子自旋和角動量的耦合

p 軌道冷原子系統的實驗實現給研究軌道自由度提供了一個有利的工具.在軌道物理中,一個有趣的方向是自旋-軌道耦合.在之前的冷原子實驗中,人們借助激光構建人工規范場,從而實現了冷原子系統中的自旋-軌道耦合[168-191].自然而然地,對于高軌道玻色系統,其中的自旋自由度和軌道自由度的相互作用會不會帶來有趣的物理效應[192,193]? 本課題組首先研究了正方晶格中的兩組分p 能帶玻色系統,相較于之前的相關研究[71,72,77],引入了自旋自由度,希望研究自旋角動量與軌道角動量的相互作用[194].表示格點r位置的湮滅算符,ν=x,y表示 px和 py軌道自由度,σ=↑,↓表示不同的組分(贗自旋).為了簡便,引入旋量,哈密頓量可以寫成

此時態 |χc〉仍是守恒量,而 |χs〉則不再守恒.由于相互作用的調制,系統的基態變成了 |χs〉.此時,系統的基態便出現了自發的自旋角動量耦合±ρ,稱之為SAI 相(spin angular-momentum interwined superfluid).在這種相中,原子的軌道角動量與自旋角動量鎖定在了一起,即自旋向上的原子的軌道角動量為px+ipy,自旋向下的原子的軌道角動量鎖定為px-ipy,如圖7(a)[194]所示.

圖7 (a) SAI 相的示意圖,在SAI 相中,由于自發的自旋-軌道耦合,粒子的自旋自由度和軌道自由度相互鎖定;(b)在不同相互作用強度下,SAI 相的穩定性;(c)在不同的溫度下,SAI 相的穩定性;(d)粒子數填充 〈n〉=2 時,玻色動力學平均場方法得到的兩組分p 軌道玻色系統基態相圖,相互作用強度設置為 U//=U⊥ ;(e)表為不同相之間序參量的表征,下左圖和右圖分別為t///t⊥=1 和10 時,不同填充數情況下基態相圖,下左圖的插圖為相變時序參量的變化.相互作用強度設置為 U//=U⊥ [194]Fig.7.(a) Pictorial illustration of SAI order.In presence of spontaneous spin angular-momentum coupling,the phase of spatial wave-function is entangled with the internal degrees of freedom of an atom in each optical lattice site.(b) Stability of SAI order against interaction quantum fluctuations.(c) Stability of SAI order against thermal fluctuations.(d) Phase diagram of the spinful porbital system with an even integer filling.The phase diagram is obtained via BDMFT.The atomic filling is fixed at 〈n〉=2,we set U//=U⊥ .(e) Table is the characterization of different quantum phase.Left and right picture are phase diagrams of spinful porbital bosons at generic fillings for t///t⊥=1 and 10 .The inset in left shows the evolution of the order parameters.We use interaction strengths U//=U⊥ [194].

為了證明上述的理論預測,采用玻色動力學平均場理論來計算系統基態,得到的基態相圖如圖7(d)和圖7(e)[194]所示.可以看出,SAI 相是系統處于超流態時的基態,而在強相互作用區間的基態分別是無序絕緣態(UI)和有序絕緣態(OI).為了證明SAI 態的魯棒性,分別計算了不同相互作用比例U⊥/U//和不同的熱漲落下,SAI 相的相變曲線,如圖7(b)和圖7(c)[194]所示.同時計算了不同的躍遷比例下,整個系統的基態相圖,也證明了SAI 相的穩定性.

5.2 六角光晶格中自旋誘導的軌道阻挫效應研究

其 中,Jx<0 ,是與鍵的方向em相關的.自旋-↑的有效自旋模型說明,在缺少自旋自由度的時候,強關聯區間Mott 相應是一個反鐵磁性,而自旋自由度將會誘導出平面內的軌道阻挫相,如圖8(b)[202]所示.在躍遷振幅為零時,系統是無軌道極化的自旋單態,而在強關聯區間的量子相是軌道阻挫相,說明在Mott 絕緣態時也存在一個相變.

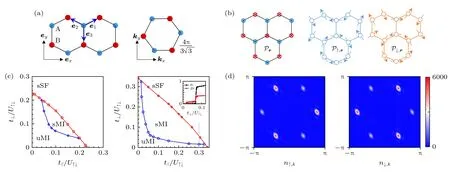
圖8 (a)左圖為二維六角晶格的幾何結構,晶格的格矢為 em ,右圖為晶格的第一布里淵區.(b)強關聯區間軌道極化矢量 P 在實空間的分布圖.左圖為無自旋玻色子的Ising 型結構,中間和右圖分別為自旋向上、自旋向下玻色子的平面內軌道渦旋結構.(c)粒子填充數 〈n〉=2 時,實空間玻色動力學平均場得到的兩組分六角晶格p 軌道玻色系統多體基態相圖.左圖和右圖的相互作用分別為 U↑=U↓=U↑↓ 和 U↑=U↓=2U↑↓ .右圖的插圖為右圖灰色垂直線路徑下,序參量的相應變化.(d)不同自旋組分在動量空間下密度的分布[202]Fig.8.(a) Geometry of two-dimensional hexagonal lattice with lattice vector em (left),and the first Brillouin zone (right).(b) Cartoons of real-space orbital polarization P for strongly interacting many-body phases in p-orbital bands of the two-dimensional (2D)hexagonal lattice,where left picture is spinless bosons demonstrate out-of-plane Ising-type orbital order,middle and right are spinful case in-plane orbital textures.(c) Hopping-dependent phase diagrams of spinful bosonic gases in p-orbital bans of a 2D hexagonal lattice for fixed filling 〈n〉=2,obtained via real-space bosonic dynamical mean-field theory.The left and right are set U↑=U↓=U↑↓ and U↑=U↓=2U↑↓ .Inset picture is the evolution of order parameter along the gray vertical line.(d) Momentum-space distributions of density nσ,k [202].

為了驗證上述結果,采用實空間玻色動力學平均場方法進行數值計算,得到的結果如圖8(c)[202]所示.在Mott 絕緣區,當t//≈t⊥時,Mott 相表征為P2≠0 的sMI 相(spin-orbital interwined Mottinsulating),對應的動量空間密度凝結在Q±=,見圖8(d)[202].系統還存在兩個量子相,一個是Mott 區的無軌道極化P2=0 的uMI相(unordered Mott-insulating),另一個是P2≠0和ρc≠0 的sSF 相(spin-orbital intertwined superfluid).

6 結論與展望

本文主要回顧了本課題組利用玻色動力學平均場理論對光晶格中強關聯玻色體系進行的一系列研究.主要結果可以概括為: 基于BDMFT 計算了三維光晶格中自旋-1 超冷玻色氣體在零溫和有限溫下的相圖,發現了自旋單態凝聚相的存在,并觀察到超流體可以通過一階(二階)相變被加熱成具有偶(奇)填充的莫特絕緣體.在存在磁場時,基態簡并被打破,體系中存在非常豐富的量子相,如向列相、鐵磁相、自旋單態絕緣相、極化超流以及軸對稱破缺超流,此外還觀察到了多步凝聚.進一步計算了自旋-1 堿金屬原子與自旋-0 堿土金屬原子混合體系的零溫相圖,發現系統表現出非零磁性長程序,當填充數n=1 時表現為二階莫特絕緣-超流體相變,當填充數n=2 時,表現為一階莫特絕緣-超流體相變,還觀察到了由于質量不平衡帶來的兩步莫特絕緣-超流體相變.在對長程相互作用的研究中,首先利用里德伯原子進行了研究,發現了兩種不同的超固體相,隨后在原子與高精細腔耦合的體系中通過控制泵浦光的反射,實現了耦合到不同軌道的超輻射相.最后對高軌道玻色體系進行了研究,首先在正方晶格中提出了一種基于多體關聯和自發對稱性破缺的自旋-軌道角動量耦合的新機制,然后在六角晶格中研究了阻挫效應,基于對稱分類,發現軌道阻挫和強相互作用之間的相互作用導致了奇異的莫特絕緣相和自旋軌道交織的超流體相.

總的來說,基于BDMFT 對光晶格中超冷玻色體系的自旋自由度、軌道自由度和長程相互作用進行了研究,這些體系中存在豐富的量子相,以及自旋-軌道角動量耦合效應、阻挫效應等,揭示了豐富的量子多體物理現象.目前我們的研究還只是對穩態的研究,在未來的研究中,將發展非平衡動力學平均場理論,對光晶格中的強關聯非平衡體系進行研究.