基于智能駕駛員模型算法的長期跟車車速預測研究*

繳文政 孫志強 付景順 孫鳳

（沈陽工業大學，沈陽 110870）

主題詞：車速預測算法 智能駕駛員模型 NGSIM 遺傳算法 參數標定

1 前言

當前，車速預測算法總體分為隨機型車速預測算法和確定型車速預測算法[1]。基于馬爾可夫鏈（Markov Chain，MC）的算法是具有代表性的隨機型車速預測算法[2-6]。雖然通過建立多級馬爾可夫鏈模型能夠提升車速預測的準確性，但會導致算法體量呈指數級增長。

確定型車速預測算法可分為參數型車速預測算法和非參數型車速預測算法[7]。基于非參數型車速預測算法的研究已經得到了廣泛的應用：支持向量機（Support Vector Machine，SVM）主要用于在較短的時間間隔內預測車速[8-9]；神經網絡可用于數據驅動型算法[10]，其因良好的非線性映射能力、較強的魯棒性，已廣泛應用于車速預測領域[11-15]，但這種方法依賴大量的訓練數據。

基于參數型車速預測的算法中，Rezaei 等人[16]使用自回歸移動平均（Autoregressive Moving Average，ARMA）模型，其參數通過歷史數據確定，但隨著視距增加，該模型會出現預測精度下降的問題；Kesting 等人[17]利用一種新的恒定加速度啟發式（Constant-Acceleration Heuristic，CAH）算法對智能駕駛員模型（Intelligent Driver Model，IDM）進行擴展；Li 等人[18]針對駕駛員的參數校準提出了一種新的方法；James 等人[19]對比了校準駕駛員模型中常用的8種方法，證明IDM有較高的車速預測性能。

預測精度和速度往往無法兼顧。Lefèvre 等人[20]比較了參數型和非參數型車速預測算法，在相同的試驗環境和試驗條件下，非參數模型的表現優于參數模型，然而對于長期預測，選取先進的參數模型更為合適。這主要是由于IDM 等參數模型都被設計為具有約束車輛長期行為的穩定性特性，而非參數模型僅被訓練為表示2個時間步之間目標車輛的行為。

新能源汽車的能量管理策略需要精確的車速預測作為前置條件。本文以車輛自身的速度軌跡預測為主要研究對象，以GPS、離線地圖數據庫、前視測距傳感器為信息源，建立基于智能駕駛員模型的車速預測算法。

2 IDM算法建模

受車輛、駕駛員等多重因素的影響，理論上滿足約束條件車速預測的解無窮多。為了計算出單一的速度軌跡，以更精確地預測車速，假設駕駛員對外部交通環境的反應遵循一套通用的規則。雖然相對于實際駕駛員的駕駛行為進行了很大程度的簡化，但許多駕駛員模型在此基礎上都能夠很好地反映實際駕駛員的駕駛行為。

2.1 智能駕駛員模型

Treiber 等人[21]最早提出智能駕駛員模型。IDM 的參數都具有明確的物理意義，可以直觀地展示駕駛行為的變化情況，并且該模型可以同時適用于通暢與擁堵狀態下的車速預測[20]：

式中，S0為擁堵狀態的最小車距；Smin為期望最小車距；Tgap為最小安全車頭時距；α為最大加速度；β為期望減速度；V為主車車速；V0為當前環境期望車速；VL為前車的速度；SL為主車與前車的距離。

該算法由加速策略和減速策略2個部分組成：加速策略為Vfree(V)=α[1-(V/V0)δ]，其中δ為駕駛員加速度指數；減速策略為Vbrake(Smin,V,SL)=-α(Smin/SL)2，當主車和前車的距離與期望的安全間距接近時，Smin開始發揮作用。主車加速行為由期望速度V0、最大加速度α和駕駛員加速度指數δ體現，當δ=1 時，加速度隨車速線性下降，當δ→∞時加速度恒定。有效的最小車距Smin由最小車距S0（僅與低速有關）、與速度相關的距離VTgap（對應于以恒定的期望時間間隔Tgap跟隨前車）和與前車的動態車速差(V-VL)決定。

為提高IDM的車速預測精度，需要足夠多可供預測的輸入數據。本文通過考慮3 個方面將不同類型的輸入數據集成到改進的智能駕駛員模型中：

a.加速度極限αmax，用于模擬車輛動力系統提供牽引力的能力；

b.速度限制Vlim，用于整合交通環境的速度限制、停車和轉彎；

c.最小車距S0、行車時距Tgap、駕駛員加速度指數δ、駕駛員減速度指數b及法定限速度的駕駛員偏差系數γ，用于參數化表示駕駛員行為。

本文使用改進的駕駛員行為模型實現基于模型的速度預測，IDM的輸入分別為Vlim、VL和SL，考慮到車速預測過程中駕駛員的減速行為直接影響預測精度，將減速策略中的固定指數2 改為可調的駕駛員減速度指數b，以便于后續參數標定。優化后算法如下：

式中，(k+1)為(k+1)時刻的預測速度；(k+1)為(k+1)時刻預測的覆蓋距離；Ts為采樣時間；Vlim為所需的期望速度或在探測器探測范圍內交通環境對車速的限制；S(k)為k時刻預測車輛行駛的距離；V(k)為k時刻的主車車速；VL(k)為k時刻的前車車速；βmax為最大減速度。

圖1所示為速度預測器的方法和架構。

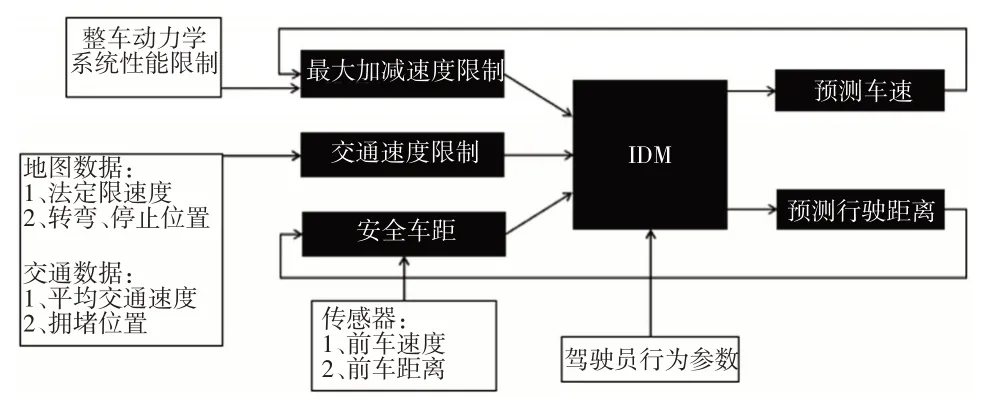
圖1 速度預測器框架

2.2 車輛動力系統限制

在傳統的IDM 研究中，多數研究者將IDM 的加速度計算為恒定的最大加速度αmax，但其通常無法充分表達復雜的動力系統行為和動力系統極限。在動力系統的限制下，加速度應與車速相關，車速提高，車輛的加速度減小。動力傳動極限會直接影響車輛的速度曲線，導致速度預測的準確性下降。

車輛在不同速度下的外力可計算為：

式中，Fdrag為由空氣、滾動摩擦和路面坡度施加的力；Meq、m分別為車輛的等效慣量和質量；Fprop為車輛牽引或制動系統施加的力；ρ為空氣密度；Cd為空氣阻力系數；A為迎風面積；Croll為滾動摩擦因數；θ為以弧度表示的道路坡度；Finertia為車輛的慣性力。

為使車輛加速，施加在車輪的驅動力必須能夠抵抗車輛運動時受到的外力。根據牛頓第二定律，發動機產生的多余力與合成加速度成正比。車輛最大加速度曲線如圖2所示。

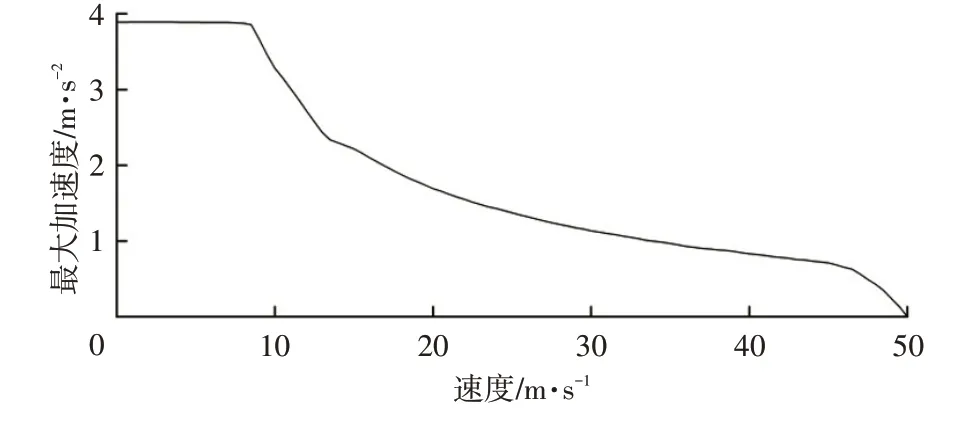
圖2 αmax曲線

2.3 交通環境的速度限制

基于交通環境的限制車速Vlim決定了在沒有前車情況下車輛的加速度。當前車速V(k)與Vlim的比值決定了駕駛員對車輛加速或減速的期望：如果V(k)/Vlim>1，改進IDM算法將產生減速請求；在沒有前車或與前車距離較遠的情況下，V(k)/Vlim<1，改進IDM 算法將產生加速請求。由車輛傳感器探測到的前方路況和線上實時交通數據等信息都將納入Vlim的考慮范圍，主要包括當前路段的法定車速限制、交通擁堵時的動態車速限制、停止標識限制、車輛轉彎時的車速限制。

式（4）中交通環境的速度限制Vlim實現方法為[17]：

式中，VL1為法定限速度限制；VL2為動態交通平均速度限制；VL3為車輛停止-起步速度限制；VL4為車輛轉彎速度限制；VSL為車輛行駛位置的法定限速度；Vtraffic為交通擁堵造成的動態平均速度限制；Sstop,i、Sturn,i分別為第i個停止位置和轉向位置與預測初始點的距離；fstop、fturn分別為車輛停止位置和轉彎位置的車速限制系數。

圖3 所示為經大量實車行駛車速數據擬合而成的停止和轉彎的車速限制系數，對停止和轉彎事件具有良好的預測性，也體現了車輛在停止和轉彎位置的速度變化情況，可使車速預測模型具有更高的精度。

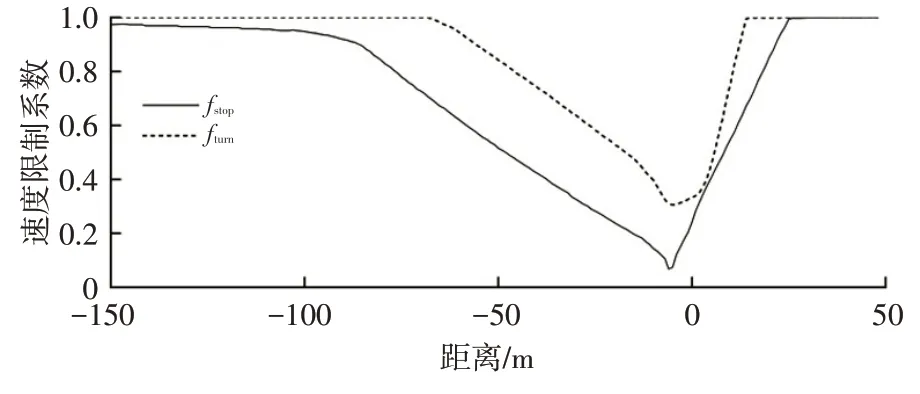
圖3 停止和轉彎的車速限制系數

2.4 駕駛員參數

在改進的IDM 中主要用5 個參數對駕駛員行為進行參數化：S0、Tgap、γ、δ、b。其中，δ可直接影響車輛的加速過程，b可直接影響車輛的減速過程，γ直接決定車輛的穩定行駛速度。而S0和Tgap相對更難確定，存在很多不確定因素，但二者對于車速預測的精度影響較小。

3 驗證數據的來源及處理

本文所使用的仿真分析數據主要來自NGSIM（Next Generation Simulation）數據集，其具有數據開源、采集頻率高、數據精準、車輛信息類型豐富等優點。基于以上優點，本文利用其中的US-101 數據集對改進的IDM的參數進行標定，該數據包的數據種類及釋義如表1所示。

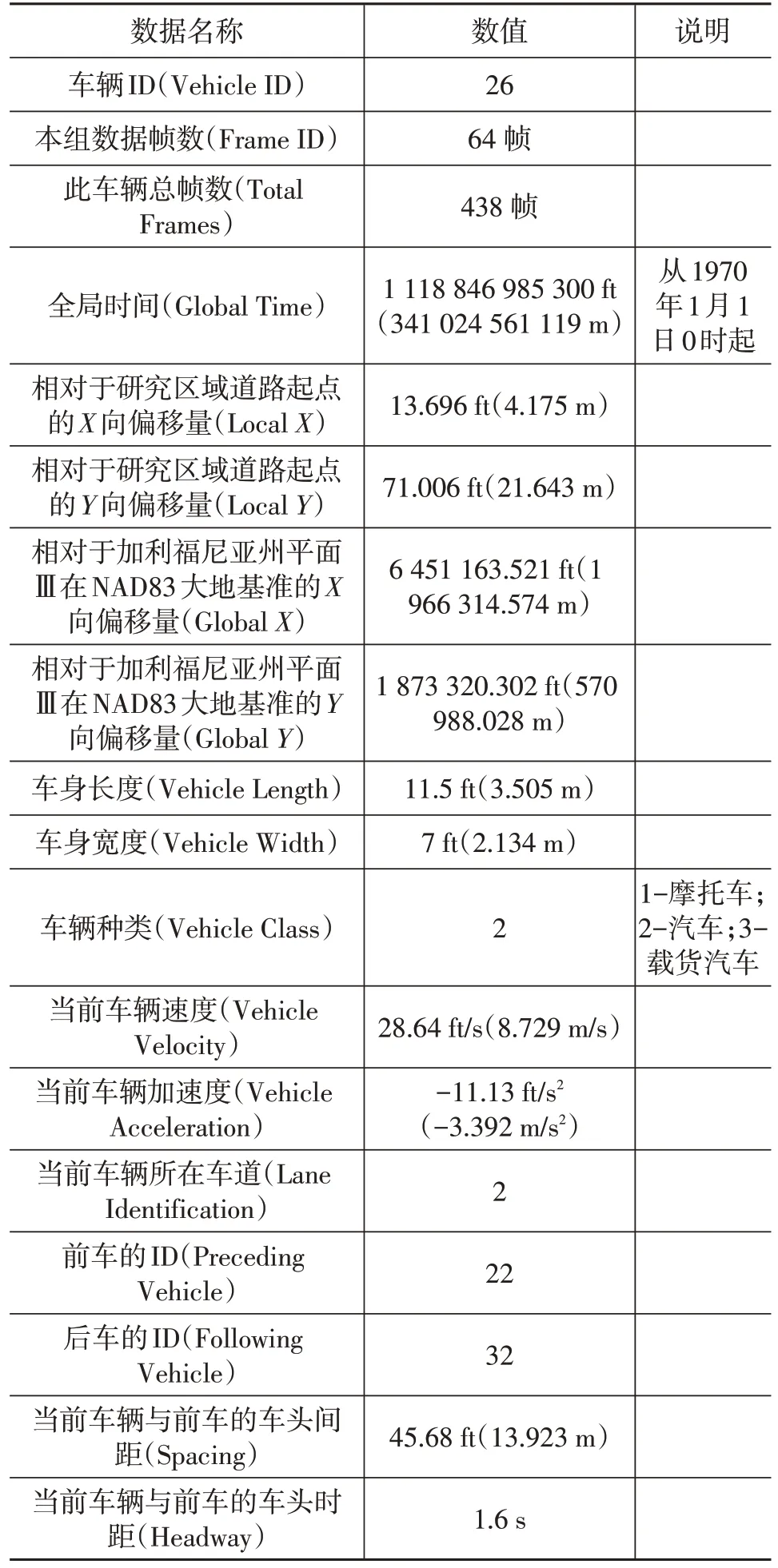
表1 數據種類及數據釋義

由于數據過于龐雜，并非所有數據均滿足改進的IDM 參數調試、標定的需求，因此必須從數據集的原始數據中篩選出滿足相關要求的數據。具體篩選條件為：

a.只選取一直位于同一車道上的車輛。

b.所選取的車輛前方應一直存在車輛，即車隊中的第1輛車不作為主車。

c.不同車型的車輛性能存在較大差異，因此選取主車時應排除摩托車和卡車車型，只選取小型汽車作為主車。雖然不同品牌、不同排量的家用轎車也存在性能差異，但由于NGSIM 項目中的US-101 公路數據為交通相對擁堵時的數據，因此小型汽車之間的性能差異可以忽略。

部分篩選結果如表2所示。

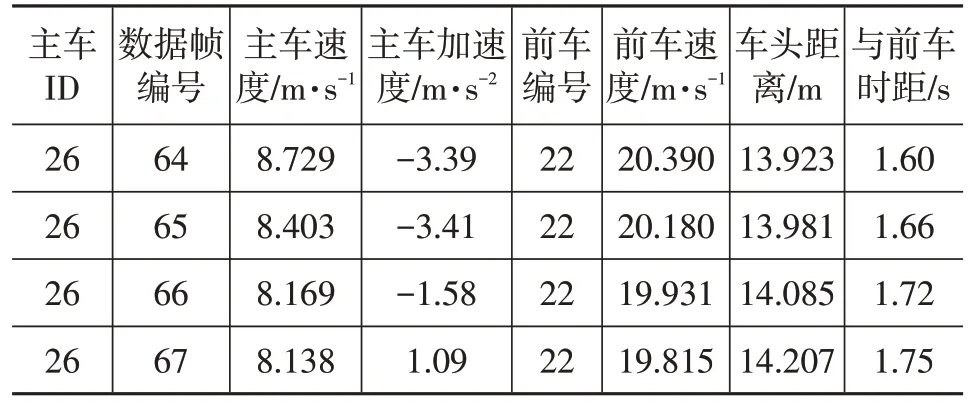
表2 部分篩選結果示例

4 參數標定及校核

改進的IDM 的參數標定及校對過程可視為非線性規劃問題求最優解的過程，本文的參數標定通過優化算法尋優的方法完成。

標定過程主要包含仿真輸入、仿真算法、仿真步長及仿真結果輸出4 個部分。仿真輸入主要包括主車的速度、主車的加速度、前車的速度、主車與前車的距離和時距等。仿真算法即為2.1 節中改進的車速預測模型。

4.1 優化算法的選取

遺傳算法（Genetic Algorithm，GA）用于解決尋優問題，吸取了Darwin的進化論和Mendel的遺傳學理論，具有良好的自適應和尋優能力[22-24]。

目標函數是預測車速與實際車速的誤差，需優化的變量是車速預測模型參數，約束是模型參數的物理邊界。由于對目標函數的收斂要求，本文采用MATLAB搭建遺傳算法來求解近似最優值，遺傳算法框架如圖4所示。

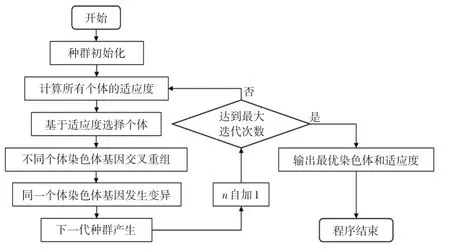
圖4 遺傳算法框架

a.初始化。確定種群規模N、交叉概率、變異概率和終止進化準則；隨機生成個體作為初始種群X(0)。

b.計算或估計X(t)中各個體的適應度。

c.選擇母體。從X(t)中運用選擇算子選擇出M/2對母體（M≥N）。

d.交叉重組。對所選擇的M/2對母體，依概率執行交叉形成M個中間個體。

e.發生變異。對其中M個個體分別獨立依照概率執行變異，形成M個候選個體。

f.選擇子代。從M個候選個體中依適應度選擇N個個體組成新一代種群X(t+1)。

g.結束程序。如已滿足終止準則或達到最大迭代次數則終止程序，輸出最優染色體和適應度。

本文具體校準程序選擇Ossen 和Hoogendoorn 推薦的目標函數[25]：

式中，H為預測樣本總量；ahsim為車輛h預測的加速度；ahreal為車輛h的實際加速度。

4.2 車速預測模型參數標定結果

根據NGSIM 項目中的實際數據及遺傳算法的應用，可以得到改進后的IDM 最優取值，如表3 所示，αmax已在前文中確定。

表3 參數標定結果

5 車速預測算法的仿真結果

本文仿真采用的計算機的中央處理器為酷睿i9-10980XE，在Simulink 模塊中建立控制算法和整車動力學模型，然后接入PreScan軟件中進行聯合仿真[26]，仿真架構如圖5所示。

圖5 聯合仿真框架

5.1 車速預測算法仿真環境的建立

5.1.1 交通環境設置

建立與US-101數據采集路段相同的路況。

5.1.2 車輛模型配置

車輛模型包括主車的車型和前方車輛的車型。試驗中車輛過多會使仿真速度變慢，可適當簡化環境中的車輛。

5.1.3 主車傳感器配置

選擇2 個獨立技術傳感器（Technology Independent Sensor，TIS）負責信號接收，均布置在主車的車頭，配置如表4所示。

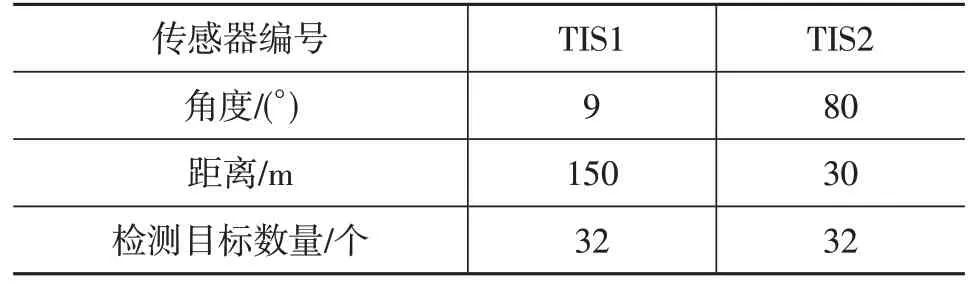
表4 傳感器配置

5.1.4 主車和前車駕駛數據設定

本文以NGSIM 項目的US-101數據集為基礎數據，選取主車及對應的前車，即可得到兩車的速度等相關數據，在仿真過程中，為與實際數據相吻合，在Simulink中插入兩車的速度插值表分別與兩車的動力學模型連接，直接由插值表控制兩車車速。

5.2 預測結果

大量文獻顯示，短期車速預測時長多集中在1 min以內，而長期車速預測多數可以超過1 min[27]，本文研究的車速預測時長為80 s。

本文將主車置于同一路段的不同交通環境下行駛，通過改變交通環境的車流量、車流速度、不同前車、不同車道等交通環境信息得到了80 s 的大量仿真結果。本文預抽取預測精度最低和最高的2組數據和1組轉彎停車行駛數據進行分析。

交通擁堵對車速有直接的影響，利用一段道路上的動態平均限速度Vtraffic、法定限速VSL和車輛在i時刻交通動態平均速度Vi（共n個時刻），構建交通擁堵程度評價函數Tseverity，可以更直觀地表達交通擁堵情況：

從式（13）中可以看出，交通擁堵程度總是正數，但由于交通過度擁堵時車速可能為0，故設定Tseverity的最大閾值為20。3次仿真過程的交通擁堵情況如圖6所示。

圖6 交通擁堵情況

在擁堵路段，前車速度是影響主車的主要因素，主車的速度主要通過前車的行為預測。IDM 的速度預測結果如圖7 所示，僅利用速度限制作為輸入數據的預測，獲得的預測車速會隨速度限制的變化而變化。

圖7 車速預測結果

圖8 所示為3 次仿真的車速誤差。從圖8a 和圖8b中可以明顯地看出，由于仿真1的交通環境擁堵程度相對于仿真2的更低，所以預測誤差更小，同時可以看出，加、減速轉換過程中誤差相對較大，由于不同的駕駛員對于前方車輛的大幅度加減速轉變所采取的反應有所不同，且反應能力不同，因此會產生較大誤差。由圖7c和圖8c 可以看出，車速預測算法中加入停止和轉彎的車速限制系數控制車輛在轉彎和停止處的車速可以很好地模擬駕駛員行為趨勢，減小車速預測算法在轉彎和停車行為中的誤差。根據上述仿真結果可以確定，優化后的車速預測算法在交通擁堵、路況復雜的環境中仍可實現較高的車速預測精度。

圖8 仿真車速誤差

圖9 所示為3 次仿真的加速度對比結果，由圖9 可知，當車速升高時，車輛的加速能力普遍不足，加速能力隨車速和擋位的升高而降低，這也更符合實際行駛中車輛的動力學性能。此外，該模型還對前車緊急制動后的加速行為表現出了一定的預判，但是，由于模型預測較為保守，預測獲得的車輛加速度相較于真實值偏低，這主要與δ和b相關，但是由于每個駕駛員的駕駛習慣不同，將這2個參數調高反而會影響此算法對其他車輛的預測精度。

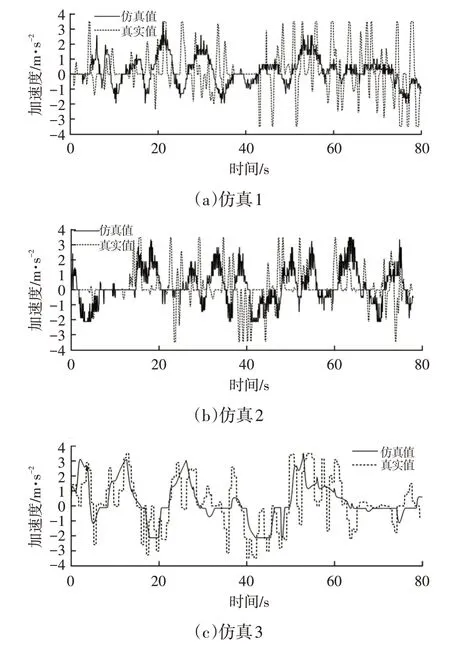
圖9 仿真加速度對比

本文使用的預測精度評價指標是均方根誤差Erms、平均絕對百分比誤差Emap：

式中，(k)、x(k)分別為模型預測的數據和車輛的真實數據；u為數據數量。

表5 列出了3 次仿真結果的車速預測誤差，由于車輛在停止（車速為0）時會引起式（14）、式（15）的失常，帶來計算上的錯誤，故在進行性能評價時忽略了車輛的停止持續時間。從圖6中可以看出，由于仿真1相對于仿真2的交通情況更加簡單，故仿真1的預測精度高于仿真2的預測精度，不同的駕駛員行為所帶來的差異更大，駕駛員的操作差異更加難以預料，故仿真2 的誤差更大。從圖7c中可以看出，仿真3雖然存在車輛轉彎和停止等事件，但加入停止和轉彎的車速限制系數控制后，仍然有著較高的車速預測精度。

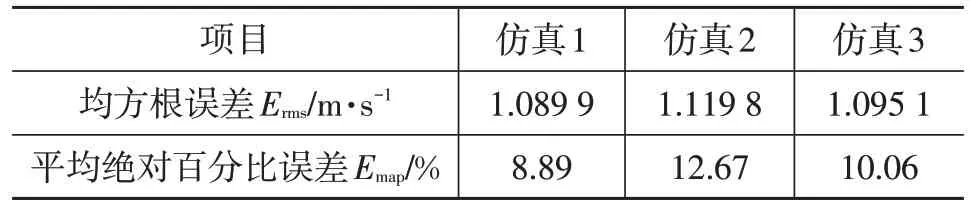
表5 車速預測誤差分析

查閱大量資料發現，在復雜的交通環境下長期車速預測平均百分比誤差通常在10%以上，而本文采用IDM跟車車速預測方法平均百分比誤差可控制在8%～13%。

路程預測結果會作為輸入重新返回到改進的IDM中，也會影響整體模型的預測精度。如圖10所示，由于車速的預測結果精度很高，路程預測結果也有著很高的精度。

由于平均絕對百分比誤差是從數據整體進行評估，故對路程預測的評價只從平均絕對百分比誤差方面分析，仿真1～仿真3平均絕對百分比誤差分別為0.024%、0.408%、0.575%，車速預測結果雖然有一定的波動性，但整體的路程預測精度依然很高。

6 結束語

本文系統地概括了影響車輛速度的道路交通特征和相應的前瞻數據，建立了具有車輛和車輛動力系統的參數化模型及基于前瞻性數據的速度預測器，通過對2條性質不同路線的仿真研究，證明了預測器處理不同水平的前瞻信息和提供準確預測的能力。

此外，可以觀察到預測精度最低和最高水平的前瞻數據之間的差異取決于交通環境的特征。高速公路行駛工況下，觀察到有關停車標志和轉彎的前瞻性數據幾乎沒有增加優勢，因為高速公路上缺乏此類道路特征。然而，在城市的交通環境中，與僅限速的前瞻數據相比，本算法具有顯著優勢。