哈密爾頓圖的一些充分條件

許秋晨，葉淼林

（安慶師范大學 數理學院，安徽 安慶 246133）

設G=G(V,E)為n階簡單連通圖，其頂點集V=V(G)={v1,v2,…,vn} ，邊集E=E(G)為V的二元重集構成的集合，稱E中元素{u,v} (u≠v)為G的邊，邊{u,v} 簡記為uv。頂點ν的度dG(ν)是指G中與v關聯的邊數，G的最小度記作δ。Kn是n階的完全圖，Km,n為完全二部圖。設G1=G(V1,E1)與G2=G(V2,E2)是兩個不交的簡單圖，它們的并圖為G1?G2=(V1?V2,E1?E2)，又記為G1+G2；如果G1=G2=…=Gk，用kG1來表示G1?G2?…?Gk；G1和G2的聯圖為G1∨G2，即在G1?G2中添加G1中每個頂點到G2中每個頂點的邊所得到的圖。

圖G的鄰接矩陣為A(G)=[aij]n×n，當vi,vj相鄰時，aij=1，否則aij=0 ，i,j=1,2,…,n，我們稱A(G) 的最大特征值為圖G的譜半徑，用ρ(G) 來表示，簡記為ρ。設D(G)=diag(d(v1),d(v2),…,d(vn)) 是圖G的度對角矩陣，定義圖G的無符號拉普拉斯矩陣Q(G)=D(G)+A(G) ，Q(G) 的最大特征值被稱為圖G的無符號拉普拉斯譜半徑，記作q(G)，簡記為q。

通過G中所有頂點的圈叫哈密爾頓圈，含有一個哈密爾頓圈的圖叫做哈密爾頓圖。圖的哈密爾頓問題一直是圖論中的經典問題，但是迄今為止，圖的哈密爾頓問題依舊NP-完全問題，還沒有被完美的解決，還有很多問題值得被研究。目前，已經有許多學者從邊條件、譜半徑以及無符號拉普拉斯譜半徑出發，對圖的哈密爾頓性進行了研究，也得出了一些結論。如周倩楠等人[1]借助邊的大小給出了圖是哈密爾頓的充分條件，后又[2]通過譜半徑以及無符號拉普拉斯譜半徑給出了哈密爾頓圖的一些充分條件；徐奕等人[3]從圖的大小，譜半徑以及無符號拉普拉斯譜半徑出發，給出了圖是哈密爾頓-連通的一些充分條件；余桂東等人[4]研究了具有較大最小度的平衡二部圖的可跡條件和哈密爾頓的譜充分條件。受周倩楠等人理論的啟發，本文主要改進圖的邊數條件，提出了哈密爾頓圖的邊充分條件，并在此基礎上給出了哈密爾頓圖的譜充分條件。

1 預備知識

引理1[1]設G是階數大于6，邊數為m的簡單圖，且δ（G）≥6，若，則G包含哈密爾頓圈，除非G∈NC。

引理2[5-6]設G是一個連通圖，如果H是G的子圖，則ρ(H)≤ρ(G)，q(H)≤q(G)，當且僅當H是G的真子圖時不等式嚴格成立。

引理3[7]設G是階數大于4 的圖，且度序列為(d1,d2,…,dn)，如果不存在一個整數，使得dk≤k，dn-k≤n-k-1，則G是哈密爾頓圖。

引理4[8]設G是有n個頂點m條邊的連通圖，則有，當且僅當G=Kn或G=K1,n-1時等號成立。

引理5[9]設G是有n個頂點m條邊的簡單圖，則，如果G是連通圖，當且僅當G=Kn或G=K1,n-1時等號成立；如果G不是連通圖，當且僅當G=Kn-1+v時等號成立。

2 主要結果

定理1 設G是階數大于6，邊數為m的簡單圖，且δ（G）≥6，若，則G是哈密爾頓圖，除非G∈NC?NP。

由引理1可知，G是哈密爾頓圖，除非G∈NC。

假設G不是哈密爾頓圖，設G的度序列為(d1,d2,…,dn)，且d1≤d2≤…≤dn，di=d(vi)，i∈{1 ,2,…,n}。

由定理條件得

因此(k-3) (2n-3k-10)≤2，因此接下來將分成四種情況來進行討論。

情形2.1 (k-3)(2n-3k-10)=2

在這種情形下，有k-3=2 且2n-3k-10=1或k-3=1 且2n-3k-10=2，我們可以得到k=5，n=13 或k=4，n=12，均與k≥6 矛盾，所以此種情形排除。

情形2.2 (k-3)(2n-3k-10)=1

在這種情形下，有k-3=1 且2n-3k-10=1，此時我們找不到滿足條件的k和n。

情形2.3 (k-3)(2n-3k-10)=0

在這種情形下，有k-3=0 或2n-3k-10=0，而k-3=0，即k=3，與k≥6 矛盾，所以此種情形排除，因此，只有 2n-3k-10=0 ，即，我們可得n≤19。

通過計算，我們可得k=6 ，n=14 或k=8 ，n=17。

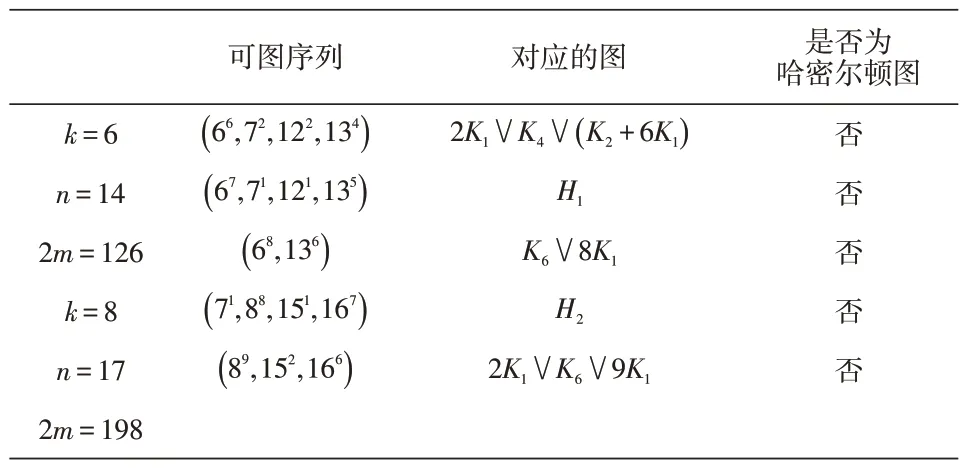
表1 情形2.3中可圖序列及其所對應的圖

情形2.4 (k-3)(2n-3k-10)＜0

因為k≥6 ，所以 2n-3k-10 ＜0 ，即，又因為，因此我們可得13 ≤n≤19。

情形2.4.1n=19

與2n-3k-10 ＜0 矛盾，所以此種情形排除。

情形2.4.2n=18

情形2.4.3n=17

情形2.4.4n=16

情形2.4.5n=15

當k≤6 時，2n-3k-10=20-3k＞0 ，與2n-3k-10 ＜0 矛盾，所以此種情形排除。

當k=7 時，2n-3k-10=-1 ＜0，此時d7≤7，。所有可圖的度序列及其對應圖如表2所示。

表2 情形2.4.5中可圖序列及其所對應的圖

情形2.4.6n=14

情形2.4.7n=13

圖1 H1 ～H23

表3 情形2.4.7中可圖序列及其所對應的圖

定理2 設G是階數大于6，邊數為m的連通圖，且δ（G）≥6，如果，則G是哈密爾頓圖。

表4 圖的譜半徑和無符號拉普拉斯譜半徑

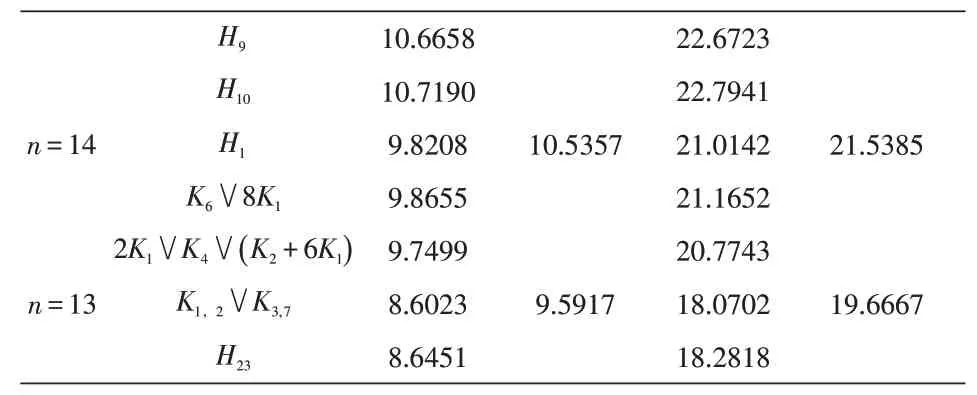
H9 n=14 H10 H1 10.5357 21.5385 K6 ∨8K1 2K1 ∨K4 ∨()n=13 K2+6K1 K1，2 ∨K3,7 9.5917 19.6667 H23 10.6658 10.7190 9.8208 9.8655 9.7499 8.6023 8.6451 22.6723 22.7941 21.0142 21.1652 20.7743 18.0702 18.2818

定理3 設G是階數大于6，邊數為m的連通圖，且δ（G）≥6，如果，則G是哈密爾頓圖，除非G=K6∨7K1。

3 結語

本文從邊條件、譜半徑以及拉普拉斯譜半徑出發，來探討圖的哈密爾頓性，并結合相關引理進行了分類討論，找到了判定圖的哈密爾頓性的改進充分條件，豐富了圖的性質研究。