單元教學背景下復習課的實踐探究
管軍


[摘? 要] “新課程、新教材、新高考”背景下的學科教學以培養學生核心素養為導向,單元復習課應基于整體把握單元主線,進一步關注知識間的相互關系和內在邏輯,關注不同層次學生的知識遷移情況和問題解決能力.單元教學背景下的復習課向學生滲透基本的數學思想方法,使學生認識數學學科知識發展的規律與特點,形成以學生為主體、以素養為主線、以問題為主導的單元復習路徑,讓數學學科核心素養的發展與提升落到實處.
[關鍵詞] 高中數學復習課;單元教學設計;整體;知識系統
問題提出
《普通高中數學課程標準(2017年版2020年修訂)》提出了數學學科核心素養六大組成要素:數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析. 數學運算是其中之一. “運算”貫穿數學的基本脈絡,是數學課程的主線,幾乎滲透到數學的每一個角落. 因此,運算求解能力是學生的基本功,發展學生的數學運算素養是數學教學的重要任務.
數學知識本身具有高度的系統化和結構化,知識內部存在著緊密的聯系. 在實際教學中,一線教師常用習題講評、錯題再練等方式單純地對學生進行鞏固性訓練,這種機械刷題式的復習只是在數量上增加了訓練,缺少了整體的統籌規劃,未能把握知識形成的主線,思維發生不了質變.單元教學以思維發展為主線,關注學生在學習過程中素養的發展,整合教學資源,連接各種知識要素,對數學概念、知識表征形式、思想方法再建構,促進學生的能力提升.單元復習能實現知識再回顧、方法再鞏固,穿點成線,連線織網,是促進學生整體把握數學知識的重要手段.本文以“指數與對數”的復習為例,進行知識梳理、方法歸納和實際應用,探索有利于學生數學核心素養發展的單元復習教學.
教學案例
1. 教學內容的分析
本課的教學內容選自《普通高中教科書·數學·必修第一冊》(蘇教版). 數學概念既是數學思維的基礎,又是數學思維的高度結晶,建立概念間的聯系,形成概念體系是建構清晰的認知體系的前提.本章從初中已有的指數概念出發,建立了根式、指數冪的概念,在此基礎上,給出對數的定義,并研究對數的運算性質.基于單元教學的理念,本課引領學生構建指數與對數單元知識結構,深化指數、對數的概念,感受它們的聯系,理解指數運算和對數運算的統一性.
2. 學生情況的分析
本課的教學對象是高一年級的學生. 經過集合、常用邏輯用語、指數與對數的學習,學生初步了解了高中與初中教學內容的異同,體驗了高中數學知識的研究方法. 經過集合運算的學習,雖然學生的抽象思維能力得到了一定的鍛煉,但是學生對對數的認識與理解仍存在困難,不能熟練運用,也沒有深刻理解指數與對數的聯系.
3. 教學目標的分析
以學生為主體,引導學生回顧指數、對數概念形成的過程,體驗數學發現和運用的歷程,提高學生的理性思維. 以素養為主線,通過對指數、對數運算定義的理解,指數、對數運算性質的比較以及運算性質的綜合運用,讓學生經歷知識再創造的過程,發展學生的數學抽象、數學運算等素養. 本課以問題為主導,從整體把握的角度出發,對教學內容進行重構,以指數與對數的比較,引導學生理解知識間的聯系,建立知識結構.通過本課學習,幫助學生掌握單元復習的方法,形成建構知識結構體系的意識.
4. 教學過程設計
環節1 比較概念,培育數學抽象的意識.
引入:從23=8開啟旅程.
問題1 觀察上式,我們研究一般等式ab=N,你能用b,N表示a嗎?你能用a,N表示b嗎?指數與對數之間的內在關系是什么?
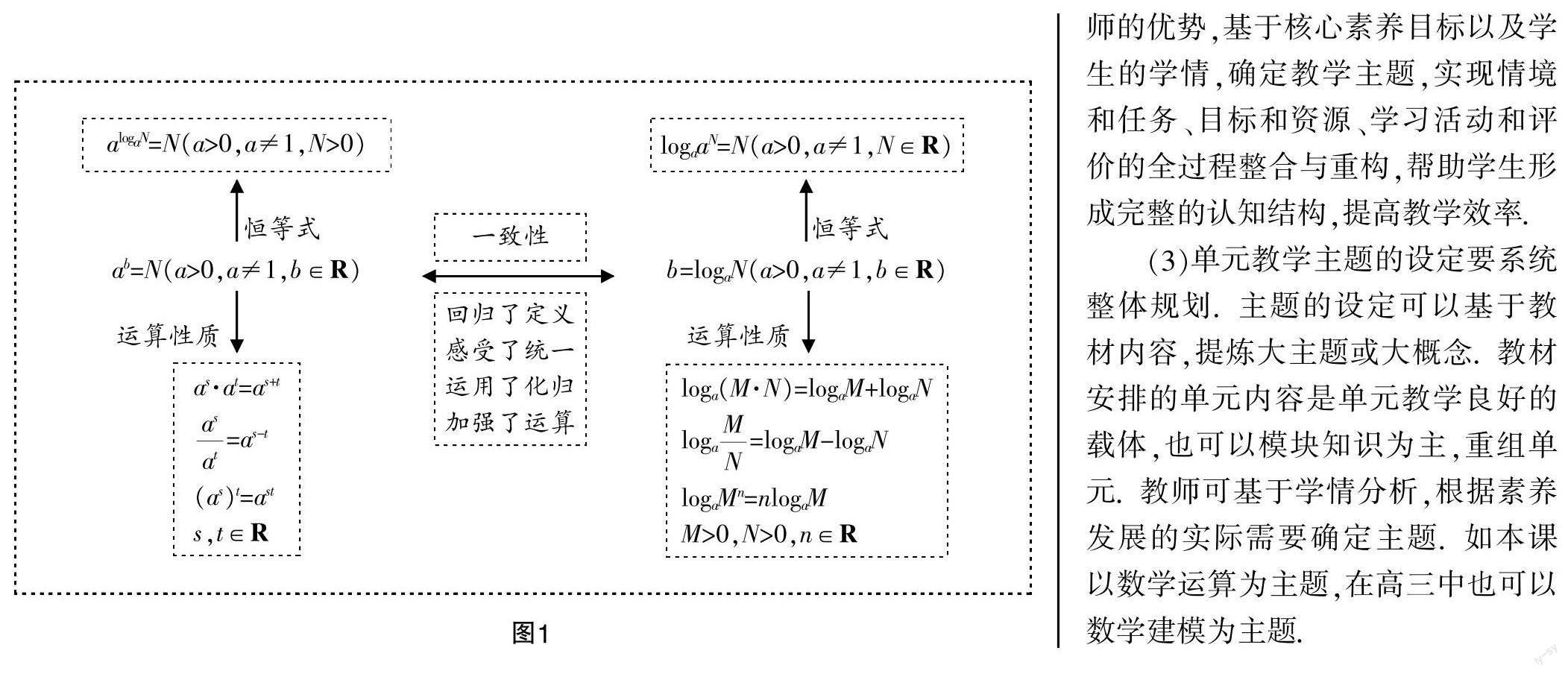
設計意圖 以復習指數、對數的概念為開始(概念如表1所示),引導學生經歷知識結構體系的建構過程.以指數概念為基礎,回顧對數的定義,使學生初步感受概念的統一性,為進一步研究指數、對數的運算性質打下基礎.
環節2? 較規律,加深運算性質的認識.
問題2 在等式有意義的前提下,a=,ab=N,logaN=b三個等式所表示的是同一關系.你會用定義證明alogaN=N和logaab=b這組等式嗎?
設計意圖 從變量間的關系的不同表達形式入手,加深學生對概念的理解,通過等價轉化,讓學生感受知識的本源關系(變量間的關系和運算性質如表2所示).把ab=N中的指數b用logaN代換,可得alogaN=N,這個恒等式可以把正數轉化為指數冪的形式.
問題3 請同學們根據自己的理解,編制題目,并請同組的同學解答.
設計意圖 利用開放性問題增進學生對概念以及恒等式的理解和應用.學生理解的角度不同,反映了他們關注的重點不同,通過同組的交流,促進學生合作學習.
精選學生的試題:(1)
5;(2);(3)eln3;(4)log22.
設計意圖 選擇代表性的試題進行展示,肯定學生的學習成果,有利于激發學生的學習興趣.從試題不同角度進行考查,全方位回顧本課的知識,加深學生對指數、對數概念和運算性質的認識和應用.
環節3 比較應用,體現學科知識的價值.
題1 已知實數a>0,a=,求loga.
設計意圖 本題可以根據a=,求出a=
,然后代入loga求解.也可以結合目標loga,對a=取對數,得loga=log,再利用對數恒等式求解. 本題靈活運用指數、對數的定義以及其運算性質,通過一題多解,加深學生對對數定義的理解,強化學生對指數與對數的一致性的認識.
題2 已知3a=5b=15,求+的值.
變式題:設2a=5b=m,且+=2,求m的值.
設計意圖 本題涉及指數式與對數式的轉化、對數的換底公式、對數的加法運算等,知識面寬,能力要求高.通過題組,由淺入深,逐步遞進,鞏固學生對指數、對數的概念和運算法則的運用.
題3 根據有關資料,圍棋狀態空間復雜度的上限M約為3361,而可觀測宇宙中普通物質的原子總數N約為1080. 則下列各數中與最接近的是()(參考數據:lg3≈0.48)
A. 1033 B. 1053
C. 1073D. 1093
設計意圖 結合實際問題,激發學生的數學學習興趣,加深學生對數學知識的理解與應用,使學生體會數學學科的應用價值,發展學生的數學建模和數學運算等素養.
4. 板書設計
板書設計如圖1所示.
教學啟示
(1)單元教學要聚焦于概念的理解和運用,重視學生學科素養的發展. 單元教學的目標定位要超越知識和技能,使學生理解數學的本質,在梳理知識發展主線的基礎上進行拓展,站在更高的視角理解知識間的關系,建立數學學科知識內部、數學與其他學科之間的聯系,體現數學的應用價值.
(2)單元教學設計要追求“用教材教”而不是“教教材”. 單元教學可以突破知識分散的限制,充分發揮教師的優勢,基于核心素養目標以及學生的學情,確定教學主題,實現情境和任務、目標和資源、學習活動和評價的全過程整合與重構,幫助學生形成完整的認知結構,提高教學效率.
(3)單元教學主題的設定要系統整體規劃. 主題的設定可以基于教材內容,提煉大主題或大概念. 教材安排的單元內容是單元教學良好的載體,也可以模塊知識為主,重組單元. 教師可基于學情分析,根據素養發展的實際需要確定主題. 如本課以數學運算為主題,在高三中也可以數學建模為主題.

