靜力學“動態平衡過程”分析與極值探討

張大洪

(重慶市潼南實驗中學)

“靜力學的平衡”是高中物理學習中同學們最先接觸且涉及廣泛的力學問題,其貫穿整個高中物理學習過程,是高考中最基本且最重要的一類問題.靜力學平衡中的“動態過程”探討更是歷年高考屢見不鮮的考點,此類問題對高中數學三角函數知識及幾何作圖、識圖能力的要求很高.處理此類問題要遵循“動中取靜、靜中探變”的思想,最常用的方法有力矢量三角形法、相似三角形法、三角函數解析法等.

1 動態力矢量三角形作圖法

1)一個力的大小與方向均確定(恒力),另一個力的方向確定,探討第三個力的大小與方向的動態變化過程與極值.

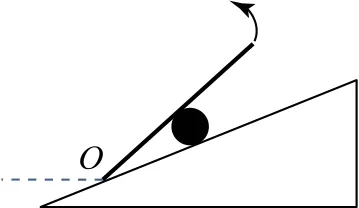
圖1

A.FN1先增大后減小,FN2一直減小

B.FN1先減小后增大,FN2一直減小

C.FN1和FN2都一直在增大

D.FN1和FN2都一直在減小

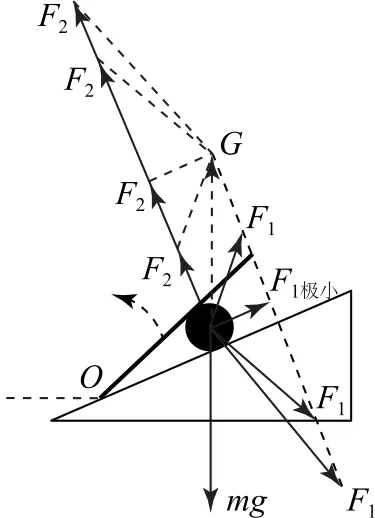
圖2

小結因二變力之合必與恒力等大反向,故以與恒力等大反向的力為合力更便于作圖,抓住一個力的方向不變,利用平行四邊形定則或三角形法則,正確表示另一個力的方向變化所引起的動態過程是處理問題的關鍵,據此來細致探討二變力的變化情況及極值.

2)一個力的大小與方向均確定(恒力),另一個力的大小確定但方向可變,探討由此力方向的變化引起的各力大小、方向的動態變化.

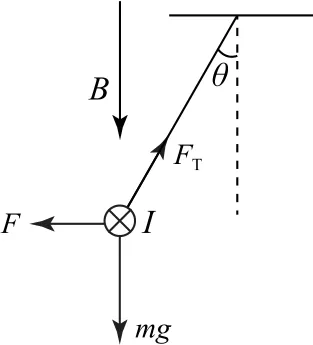
圖3

A.導線受到的安培力逐漸變大

B.絕緣細線受到的拉力逐漸變大

C.絕緣細線與豎直方向的夾角θ先增大后減小

D.導線受到的安培力與絕緣細線受到的拉力的合力大小不變,方向隨磁場方向的改變而改變

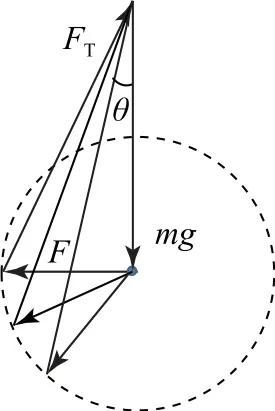
圖4

小結正確進行受力分析,充分抓住輔助圓的半徑大小不變來確保一個力的大小不變但方向可動態變化是處理問題的關鍵;注意重力為恒力且動態過程中滿足三力之和為0,即三力矢量首尾相接必構成一個封閉的矢量三角形,可直觀形象探討動態過程中物理量的變化情況.

3)一個力的大小與方向均確定(恒力),另兩個力僅大小相等且未知,而方向不確定,探討另兩個力的大小與方向的動態變化.

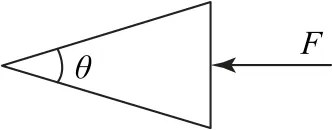
圖5

A.若F一定,θ大時FN大

B.若F一定,θ小時FN大

C.若θ一定,F大時FN大

D.若θ一定,F小時FN大

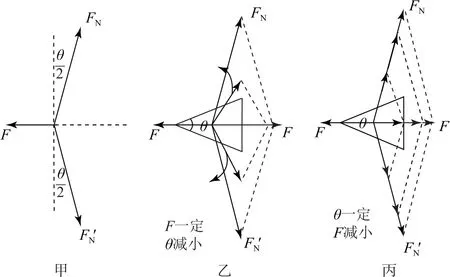
圖6

小結合理選擇合力,抓住另兩個力的特征,充分利用平行四邊形定則或三角形法則,結合動態過程的誘因探究物理量的變化情況.

4)一個力的大小與方向均確定(恒力),另兩個力的大小、方向均不確定,但此二力的夾角為定值,探討此二力的動態變化.

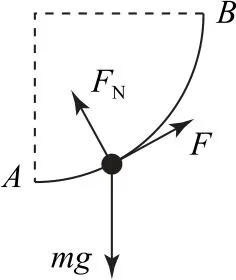
圖7

A.F增大、FN減小

B.F減小、FN減小

C.F增大、FN增大

D.F減小、FN增大

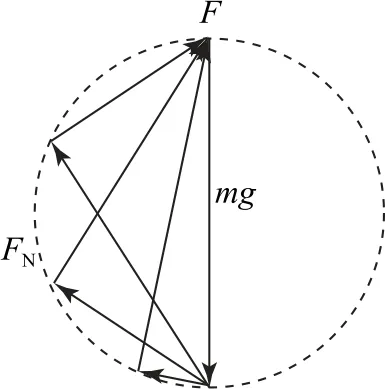
圖8

小結動態平衡過程滿足三力之和為0,即三力矢量首尾相接必構成一個封閉的矢量三角形,抓住二變力間的夾角θ及此角對應的那個力恒定不變,正確作出以此恒力為弦、以二變力間的夾角θ為此恒力弦對應的圓周角的輔助圓是解題的關鍵,即可借此輔助圓來直觀細致探討動態過程的變化情況.

5)一個力的大小與方向均確定(恒力),另兩個力的大小、方向均不確定,但其間的夾角作單調增減變化,探討二力的大小、方向的動態變化.

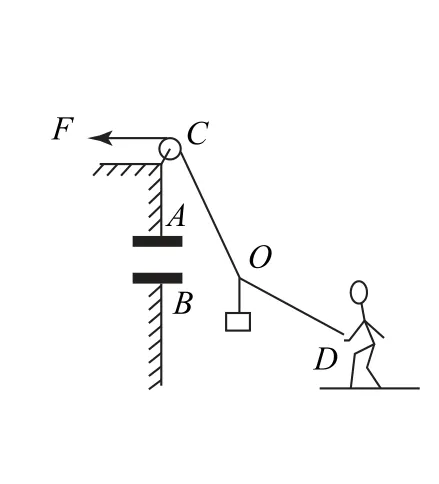
圖9

A.OC繩的拉力逐漸增大,OD繩的拉力逐漸減小

B.OC繩的拉力逐漸減小,OD繩的拉力逐漸增大

C.OC繩和OD繩的拉力均逐漸減小

D.OC繩和OD繩的拉力均逐漸增大

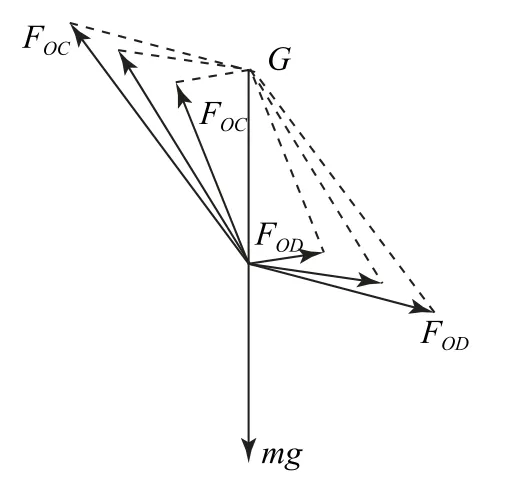
圖10

小結以與恒力等大反向的力為合力,充分利用平行四邊形定則或三角形法則,抓住二變力的特點即可進行二變力的動態過程探討.

2 力矢量三角形與幾何三角形相似法的應用

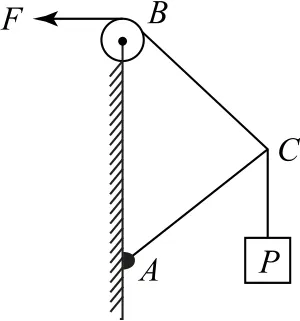
圖11

A.BC繩中的拉力F越來越大

B.BC繩中的拉力F越來越小

C.AC桿 中 的 支 持 力FN越來越大

D.AC桿 中的 支 持力FN越來越小

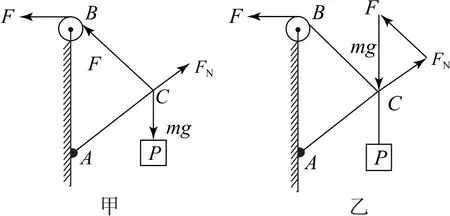
圖12

其中mg、AB、AC均不變,BC逐漸減小,則由上式知FN不變,F變小,選項B正確.

小結首先對研究對象進行受力分析,利用共點三力平衡的條件即合力為0作出三力矢量首尾相接的封閉三角形,然后抓住此力矢量三角形所對應的幾何三角形,利用相似的比例關系列出簡單的關系式,再準確判斷出動態變化過程中三力矢量與三邊幾何長度的不變量及變化量的特點與變化情況,利用比例關系式即可處理各變化量的動態變化情況.此方法能有效避免煩瑣的數學運算(特別是三角函數的運算).

3 解析法處理靜力學平衡的動態過程及極值探究

1)用三角函數的單調性分析處理動態平衡問題.

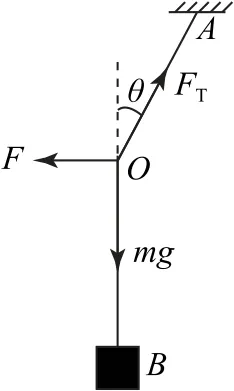
圖13

A.F逐漸變大,FT逐漸變大

B.F逐漸變大,FT逐漸變小

C.F逐漸變小,FT逐漸變大

D.F逐漸變小,FT逐漸變小

小結正確受力分析并利用平衡條件建立各力間的平衡方程,抓住各力與三角函數的單調變化關系,即可探討此類平衡的動態問題.2)用正弦定理處理動態平衡過程.

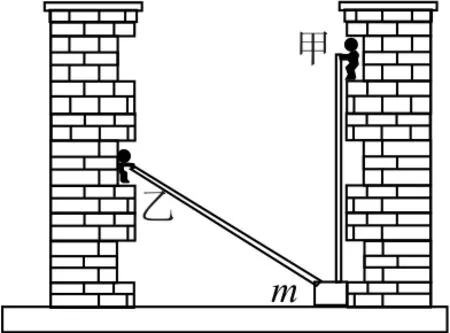
圖14

A.甲繩的拉力先增大后減小

B.乙繩的拉力先增大后減小

C.當重物接近乙處時甲繩的拉力接近

D.當重物接近乙處時乙繩的拉力接近mg

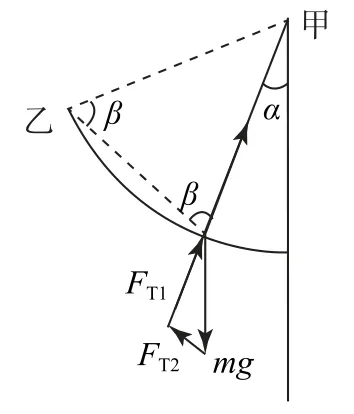
圖15

重物向乙處移動的過程中α、β均增加,設直線l甲乙與過點甲的豎直線的夾角為θ,則必有2β+(θ-α)＝180°,設α增加角度x時β增加的角度為y,則有

由此二式得x＝2y,即在動態變化過程中α角的增加值是β角增加值的2 倍,故在α、β均增加的過程中β-α必減小,即減小,則FT1始終減小,故選項A 錯誤.

因為α、β始終為銳角,且α＜β,由三角函數關系式可知

當α增加x,且β增加y時,乙對物體的拉力為F'T2,則同理有

如圖16所示,重物接近乙時,乙與重物的連線逐漸與重物的軌跡相切,兩繩間的夾角逐漸趨近90°,即兩拉力垂直,由相似三角形可得

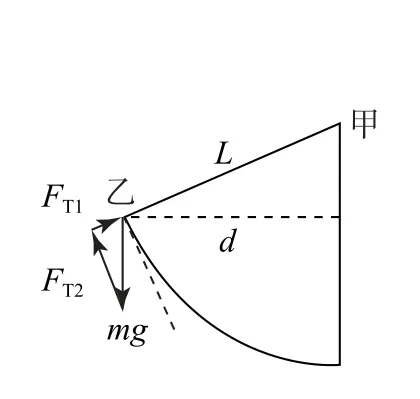
圖16

小結在用正弦定理處理靜力學平衡的動態問題時,首先要作出共點三力平衡的封閉力矢量三角形,找準其邊、角對應關系,在處理實際動態變化過程中要仔細研究角度變化的制約關系及其相應三角函數的變化情況,熟練應用三角函數運算及其變換,才能正確解決動態問題.

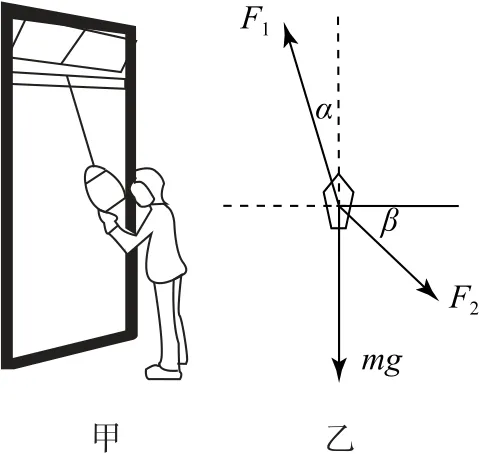
圖17

小結正確理解與應用三角變換.

圖18

4)用cos(α±β)＝cosαcosβ?sinαsinβ處理動態平衡問題.

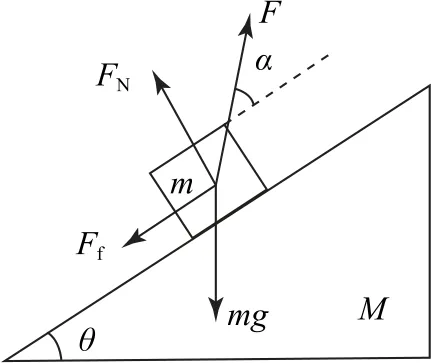
圖19

(1)α、θ間滿足什么條件時,拉力F有最小值,求此最小值;

(2)求在拉力F取最小值的情況下木楔對水平面的摩擦力.

(1)木塊在力F的作用下沿斜面向上勻速運動時其受力如圖19所示,由力的平衡條件可得平衡方程

由于θ是恒定不變的,故只有當cos(θ-α)取最大值1時,即α＝θ時,拉力F有最小值,且最小拉力為Fmin＝mgsin2θ.

(2)以M+m為整體,因木塊沿木楔勻速上升而木楔始終靜止,M+m整體處于平衡態,故整體受到地面的摩擦力等于F的水平分力,即

當F取最小值Fmin＝mgsin2θ時有

小結合理選擇研究對象,正確受力分析,利用平衡條件建立各力間的平衡方程,熟練掌握三角函數的和差化積、倍角關系等公式及其應用,結合三角函數的變化特征即能快速處理動態平衡問題中的臨界與極值問題.

5)靜力學平衡動態過程中的自鎖問題.

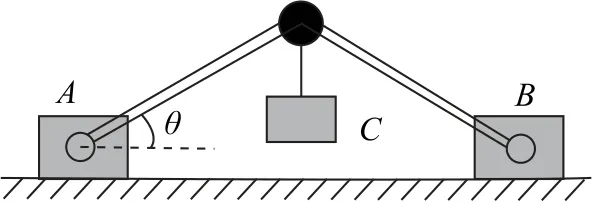
圖20

(1)求地面對物體A的靜摩擦力大小;

(2)無論物塊C的質量多大,都不能使物塊A或B沿地面滑動,則μ至少要多大?

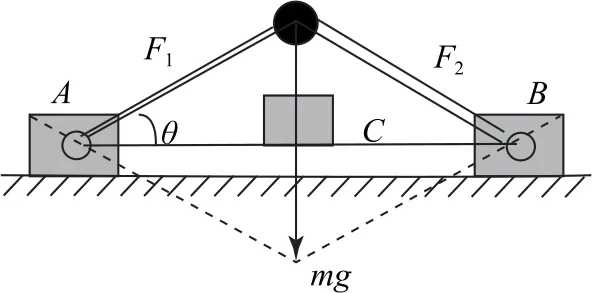
圖21

對物體A水平方向有

(2)要使A、B始終不沿地面滑動,則須滿足地面對其實際靜摩擦力小于或等于其最大靜摩擦力,即Ff≤Ffm,由于A與地面之間的最大靜摩擦力為

小結對于摩擦自鎖問題,沿自鎖面的實際靜摩擦力小于或等于此表面的最大靜摩擦力即為自鎖條件.

總之,處理靜力學平衡的“動態過程”問題時,作圖法能直觀、形象地反映出動態過程中相關物理量的大小、方向的變化情況與過程,能簡潔地反映出物理量變化中可能出現的極值,避免了煩瑣的數學運算,處理動態平衡問題會更簡便、快捷,用時更少,效率更高.但不能得出各狀態的具體數值,對幾何作圖與分析的要求也較高,抓住動態過程中某物理量的本質特性正確建立輔助圖形(輔助圓、矢量三角形、幾何三角形、平行四邊形等)是探究動態過程的關鍵.解析法能準確、細致得出動態過程中各狀態物理量的具體數值,且對多力(三個以上)平衡問題的處理也更恰當,但其對三角函數及其相應的各種變換與計算要求很高,計算過程也較復雜,因此要求同學們有充足的知識與能力儲備.

(完)