一種面向中近程導(dǎo)彈的在線彈道規(guī)劃方法

張夢典，高登巍，董詩萌，苗昊春

(西安現(xiàn)代控制技術(shù)研究所，陜西 西安 710065)

0 引言

為了滿足中近程導(dǎo)彈的適用范圍廣、精度高的作戰(zhàn)任務(wù)需求,有必要對(duì)于在線規(guī)劃彈道的方法進(jìn)行研究。在線彈道規(guī)劃,即在已知諸元信息的情況下,利用彈載計(jì)算機(jī)在線完成彈道的規(guī)劃,得到滿足各種約束的光滑彈道,使導(dǎo)彈按照在線計(jì)算的彈道飛行。與離線設(shè)計(jì)彈道的方法相比,在線規(guī)劃方法一方面能夠減小彈載計(jì)算機(jī)的存儲(chǔ)需求,另一方面能夠通過在線設(shè)計(jì)滿足各種射程的任務(wù)需求,精度相比插值計(jì)算進(jìn)一步提升。

目前,運(yùn)動(dòng)規(guī)劃在機(jī)器人、飛行器、無人車等領(lǐng)域具有廣泛的應(yīng)用。其中,RRT[1]、A*算法[2-3]是路徑規(guī)劃中常用的搜索算法,隨著應(yīng)用場景復(fù)雜性的增加,滿足微分約束的RRT*算法[4-5]、智能算法[6-7]等也得到了研究與應(yīng)用。在軌跡規(guī)劃中,多項(xiàng)式曲線[8-9]、樣條曲線[10-12]經(jīng)常被應(yīng)用,以滿足各種動(dòng)力學(xué)約束。然而,這些方法在彈道規(guī)劃中的應(yīng)用較少,應(yīng)用的可行性也未得到驗(yàn)證。

文中設(shè)計(jì)了一種在線彈道規(guī)劃的方法,具體內(nèi)容如下:1)根據(jù)少量離線設(shè)計(jì)的彈道,利用樹形結(jié)構(gòu)進(jìn)行網(wǎng)格化存儲(chǔ),大幅減小存儲(chǔ)量;2)用帶約束的分段多項(xiàng)式曲線將網(wǎng)格化曲線還原為光滑彈道,獲取控制指令的初值;3)根據(jù)控制指令的初值在線進(jìn)行三自由度彈道的積分運(yùn)算,并根據(jù)實(shí)際落點(diǎn)與期望落點(diǎn)的偏差,修正控制指令,重復(fù)上述步驟直至計(jì)算落點(diǎn)在目標(biāo)點(diǎn)附近。利用MATLAB對(duì)提出的在線彈道規(guī)劃方法進(jìn)行仿真運(yùn)算,驗(yàn)證了方法的可行性、快速性。

1 問題建立

1.1 導(dǎo)彈運(yùn)動(dòng)模型

導(dǎo)彈在飛行過程中,在主動(dòng)段發(fā)動(dòng)機(jī)推力的作用顯著,彈道的形式較為相似。文中將主要針對(duì)被動(dòng)段的彈道進(jìn)行設(shè)計(jì)。

對(duì)于中近程導(dǎo)彈而言,在被動(dòng)段除了要考慮空氣動(dòng)力、引力、控制力之外,還需考慮科里奧利力(Coridis force)慣性力和離心慣性力的作用。為了保證描述時(shí)能更好地反映發(fā)射點(diǎn)和目標(biāo)點(diǎn)的位置關(guān)系,導(dǎo)彈的位置用距發(fā)射點(diǎn)的地球弧線距離和海拔高度表示,包括發(fā)射方向上的弧線距離為d;海拔高度為h;側(cè)向距離為z。此時(shí)導(dǎo)彈的三自由度運(yùn)動(dòng)方程可以描述為:

(1)

式中:m代表導(dǎo)彈質(zhì)量;D,L,Z為導(dǎo)彈受到的氣動(dòng)力;GV為坐標(biāo)系轉(zhuǎn)換矩陣;g代表引力加速度;ωe代表地球自轉(zhuǎn)角速度與導(dǎo)彈相對(duì)地心的角速度之和;r和v分別代表導(dǎo)彈的位置和速度。

1.2 問題描述

文中針對(duì)中近程導(dǎo)彈的被動(dòng)段展開在線彈道規(guī)劃方法的設(shè)計(jì),具體要求包括:1)導(dǎo)彈落點(diǎn)在目標(biāo)附近;2)彈道平滑、連續(xù)且滿足速度、加速度的連續(xù);3)彈道滿足微分約束以及攻角、側(cè)滑角的范圍約束。

2 方法設(shè)計(jì)

2.1 彈道網(wǎng)格化與樹形結(jié)構(gòu)存儲(chǔ)

在進(jìn)行彈道在線規(guī)劃需基于一定數(shù)量的離線設(shè)計(jì)的彈道展開。為了減小離線彈道帶來的存儲(chǔ)量,對(duì)彈道進(jìn)行網(wǎng)格化,并利用樹形結(jié)構(gòu)對(duì)網(wǎng)格化后的彈道進(jìn)行存儲(chǔ)。分析表明,該存儲(chǔ)方式可大幅減小數(shù)據(jù)存儲(chǔ)量。

對(duì)彈道進(jìn)行網(wǎng)格化時(shí),針對(duì)原始彈道的射程和高度范圍進(jìn)行等間距劃分。假設(shè)射程范圍為[d1,dh],劃分為nd個(gè)網(wǎng)格,高度范圍為[h1,hh],劃分為nh個(gè)網(wǎng)格。之后,對(duì)彈道上的每個(gè)點(diǎn)(di,hi)計(jì)算網(wǎng)格化后的標(biāo)識(shí)符sd,i和sh,i,可表示為:

(2)

式中round(x)表示最接近x的整數(shù),x的小數(shù)部分恰為0.5時(shí)取較大的數(shù)。

在網(wǎng)格化存儲(chǔ)時(shí),只對(duì)于標(biāo)識(shí)符進(jìn)行存儲(chǔ),因此,標(biāo)識(shí)符完全相同且相鄰的點(diǎn)可以看作一個(gè)點(diǎn),只需存儲(chǔ)一次。因此,網(wǎng)格化存儲(chǔ)不僅減少了需要存儲(chǔ)的點(diǎn)的數(shù)量,存儲(chǔ)的數(shù)據(jù)類型也從浮點(diǎn)型變?yōu)檎?從而達(dá)到減小存儲(chǔ)量的作用。

樹形結(jié)構(gòu)存儲(chǔ),則是借鑒了RRT算法生成的樹形結(jié)構(gòu),進(jìn)一步減小數(shù)據(jù)的存儲(chǔ)量。RRT是一種路徑規(guī)劃的方法,在生成路徑時(shí)采用樹的結(jié)構(gòu)形式,即:除根節(jié)點(diǎn)外,每個(gè)節(jié)點(diǎn)有且僅有一個(gè)父節(jié)點(diǎn),且可以有多個(gè)子節(jié)點(diǎn)。RRT搜索的節(jié)點(diǎn)達(dá)到目標(biāo)點(diǎn)附近后,從該節(jié)點(diǎn)開始,依次往前尋找父節(jié)點(diǎn),由于每個(gè)節(jié)點(diǎn)的父節(jié)點(diǎn)唯一,因此可以得到一條從根節(jié)點(diǎn)到目標(biāo)點(diǎn)附近的唯一確定的路徑。

對(duì)于離線設(shè)計(jì)的彈道而言,當(dāng)彈道的目標(biāo)點(diǎn)相同時(shí),彈道末端的形式非常接近。將網(wǎng)格化彈道轉(zhuǎn)化為樹形結(jié)構(gòu),具體步驟為:

1)根據(jù)彈道目標(biāo)點(diǎn)的位置確定樹的個(gè)數(shù),每個(gè)目標(biāo)點(diǎn)對(duì)應(yīng)一棵樹,目標(biāo)點(diǎn)對(duì)應(yīng)的網(wǎng)格化后的節(jié)點(diǎn)為這棵樹的根節(jié)點(diǎn);

2)對(duì)于每條網(wǎng)格化后的彈道,根據(jù)目標(biāo)點(diǎn)找到其對(duì)應(yīng)的樹,分叉標(biāo)志設(shè)置為0;

3)從根節(jié)點(diǎn)開始倒序存儲(chǔ)彈道,每個(gè)節(jié)點(diǎn)的父節(jié)點(diǎn)為彈道上的后一個(gè)點(diǎn)。當(dāng)分叉標(biāo)志為0,且滿足該節(jié)點(diǎn)在樹中存在、樹中父節(jié)點(diǎn)與自身父節(jié)點(diǎn)相同時(shí),無需額外存儲(chǔ);否則,需將該節(jié)點(diǎn)確定為新節(jié)點(diǎn),存儲(chǔ)該節(jié)點(diǎn)及其父節(jié)點(diǎn)在樹中的位置,并將分叉標(biāo)志置為1。

通過上述步驟實(shí)現(xiàn)彈道的樹形結(jié)構(gòu)存儲(chǔ)。樹形結(jié)構(gòu)一方面避免彈道重合度高的部分的重復(fù)存儲(chǔ),另一方面可在定位樹的末節(jié)點(diǎn)后,通過查找父節(jié)點(diǎn)快速重建起網(wǎng)格化彈道。因此,樹形結(jié)構(gòu)可進(jìn)一步減小存儲(chǔ)量,且查找彈道時(shí)不存在大的計(jì)算量。

2.2 分段多項(xiàng)式彈道還原

彈道網(wǎng)格化后,精度降低,且不滿足連續(xù)性約束,無法用于計(jì)算控制指令。因此,需要將網(wǎng)格化后的彈道還原為光滑、連續(xù)、滿足攻角約束的彈道。文中采用分段多項(xiàng)式對(duì)網(wǎng)格化彈道進(jìn)行還原,將該問題轉(zhuǎn)化為帶約束的二次規(guī)劃問題進(jìn)行求解,得到高階連續(xù)且滿足約束的彈道,用于求取控制指令。

采用分段多項(xiàng)式,即將彈道分成多段對(duì)時(shí)間的參數(shù)不同的多項(xiàng)式。由于彈道是二維的,包含射程d和高度h,即需要對(duì)兩個(gè)維度分別針對(duì)時(shí)間t進(jìn)行分段,采用五階多項(xiàng)式,第i段多項(xiàng)式的公式[9]為:

pi(t)=p0,i+p1,it+p2,it2+…+pn,itn

(3)

式中:p0,i,p1,it,…,pn,i為第i段多項(xiàng)式待確定的n+1個(gè)多項(xiàng)式系數(shù)。用二次規(guī)劃的方式,將所有的多項(xiàng)式系數(shù)確定為待優(yōu)化參數(shù),將連續(xù)性條件、攻角約束等設(shè)置為等式約束和不等式約束,并根據(jù)需求設(shè)置目標(biāo),通過求解二次規(guī)劃得到多項(xiàng)式系數(shù)。二次規(guī)劃問題的基本形式[13]為:

(4)

式中:x為待求解變量;f(x)為目標(biāo)函數(shù),其中H和J分別代表二次目標(biāo)項(xiàng)和線性目標(biāo)項(xiàng);Aeq和beq分別為矩陣和向量,組成等式約束;A和b分別為矩陣和向量,組成不等式約束。

該問題的等式約束包括:

1)初始點(diǎn)的位置、速度、加速度應(yīng)與初始條件完全相同;

2)分段多項(xiàng)式所有連接點(diǎn)的位置、速度、加速度等的連續(xù)。

該問題的不等式約束包括:

1)彈道上每個(gè)點(diǎn)的位置(pd,i,ph,i)在由該點(diǎn)標(biāo)識(shí)符確定的網(wǎng)格約束范圍內(nèi),即:

(5)

2)彈道上每個(gè)點(diǎn)的加速度應(yīng)在一定范圍內(nèi),該范圍與攻角的限制范圍有關(guān)。

對(duì)于目標(biāo)函數(shù),可將其設(shè)置為分段多項(xiàng)式的n的導(dǎo)數(shù)的積分。例如,如果希望攻角的變化率較小,可將目標(biāo)函數(shù)設(shè)置為多項(xiàng)式三階導(dǎo)數(shù)的積分。

在利用二次規(guī)劃形式完成對(duì)含約束的分段多項(xiàng)式彈道的問題描述后,求解二次規(guī)劃問題,即可完成對(duì)分段多項(xiàng)式系數(shù)的求解。得到的分段多項(xiàng)式彈道在滿足彈道平滑、連續(xù)的基礎(chǔ)上,保證了高階連續(xù)及攻角不超限。利用該多項(xiàng)式彈道,可計(jì)算出每個(gè)彈道點(diǎn)對(duì)應(yīng)的攻角,給出可行、有效的控制指令。

2.3 預(yù)測校正法修正控制指令

由于離線的原始彈道是針對(duì)某一特定射程、海拔高度設(shè)計(jì),如果實(shí)際飛行的條件沒有覆蓋到,采用設(shè)計(jì)的彈道無法使導(dǎo)彈命中目標(biāo),因此有必要對(duì)彈道進(jìn)行在線調(diào)整,修正控制指令。在給出的控制指令的基礎(chǔ)上,利用預(yù)測校正法,對(duì)彈道進(jìn)行積分運(yùn)算以預(yù)測彈道終點(diǎn),并根據(jù)落點(diǎn)偏差修正控制指令,直至彈道落點(diǎn)能夠到達(dá)目標(biāo)點(diǎn)附近。

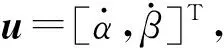
為了實(shí)現(xiàn)對(duì)控制指令的修正,再次通過二次規(guī)劃問題進(jìn)行求解。求解前的準(zhǔn)備工作包括:

1)利用狀態(tài)空間表示形式對(duì)導(dǎo)彈三自由度運(yùn)動(dòng)過程進(jìn)行線性化描述,公式[14]為:

(6)

式中:A為系統(tǒng)矩陣;B為輸入矩陣。

2)根據(jù)導(dǎo)彈動(dòng)力學(xué)方程以及每個(gè)時(shí)刻的狀態(tài)向量x(k)和控制向量u(k),對(duì)每個(gè)時(shí)刻狀態(tài)空間表達(dá)式中的A(k)和B(k)進(jìn)行推導(dǎo)。

3)利用每個(gè)時(shí)刻的A(k)和B(k),根據(jù)積分公式,建立起下個(gè)時(shí)刻的狀態(tài)變量x(k+1)與當(dāng)前時(shí)刻的x(k)、u(k)之間的關(guān)系[14]為:

x(k+1)=A1(k)x(k)+B1(k)u(k)

(7)

式中:A1(k)和B1(k)分別代表離散狀態(tài)空間的系統(tǒng)矩陣和輸入矩陣。

4)假設(shè)當(dāng)前時(shí)刻的x(k)和u(k)分別產(chǎn)生大小為Δx(k)和Δu(k)的變化,當(dāng)Δx(k)和Δu(k)較小時(shí),下一時(shí)刻狀態(tài)變量的變化近似為:

Δx(k+1)=A1(k)Δx(k)+B1(k)Δu(k)

(8)

記xn=[Δx(0)T,Δu(0)T,Δx(1)T,Δu(1)T,…,Δx(n-1)T,Δu(n-1)T,Δx(n)T]T,表示每個(gè)時(shí)刻狀態(tài)向量和控制向量的變化量,將xn作為待優(yōu)化參數(shù),按照式(4)建立二次規(guī)劃問題。

該問題的等式約束包括初始時(shí)刻狀態(tài)向量固定,因此Δx(0)=0;不同時(shí)刻狀態(tài)變量之間的關(guān)系,即式(8)。

該問題的不等式約束包括攻角、側(cè)滑角變化的范圍限制。

在設(shè)置目標(biāo)函數(shù)時(shí),為了使彈道終點(diǎn)在目標(biāo)點(diǎn)附近,即希望Δx(n)盡可能接近期望的終端條件xf與x(n)的差,因此必須在目標(biāo)函數(shù)中加入終端約束用于表示這兩者的偏差,不同維度可采用不同權(quán)重。此外,如果期望彈道經(jīng)過特定的點(diǎn),可以在目標(biāo)函數(shù)中加入航路點(diǎn)約束;如果希望向量中某一維度的變化較小,也可在H對(duì)角線對(duì)應(yīng)位置上加入權(quán)重。

由于該二次規(guī)劃問題將終端約束加入目標(biāo)函數(shù)而非設(shè)置為約束,求解該二次規(guī)劃問題只能使x(n)與xf更加接近。因此,如果這二者仍舊存在較大差距,需要在根據(jù)各個(gè)時(shí)刻的Δu計(jì)算得到的新的控制指令u的基礎(chǔ)上,再次進(jìn)行積分、修正控制指令的操作,完成多次迭代,直至彈道終點(diǎn)達(dá)到目標(biāo)點(diǎn)附近。

3 仿真驗(yàn)證

在MATLAB平臺(tái)上,對(duì)于設(shè)計(jì)的在線彈道規(guī)劃的方法進(jìn)行仿真驗(yàn)證。

采用彈道網(wǎng)格化與樹形結(jié)構(gòu)存儲(chǔ)方法,對(duì)于離線設(shè)計(jì)的大量彈道進(jìn)行存儲(chǔ)。結(jié)果表明,樹形結(jié)構(gòu)的網(wǎng)格化彈道,存儲(chǔ)時(shí)占用的空間約為原始彈道占用空間的4%,大大緩解了內(nèi)存占用的問題。

將預(yù)計(jì)進(jìn)行在線規(guī)劃的發(fā)射點(diǎn)、目標(biāo)點(diǎn)的條件設(shè)置如表1所示,進(jìn)行在線彈道規(guī)劃時(shí)所用到的離線基準(zhǔn)彈道如表2所示。其中條件1、條件2采用基準(zhǔn)彈道1,條件3、條件4采用基準(zhǔn)彈道2,條件5、條件6采用基準(zhǔn)彈道3。

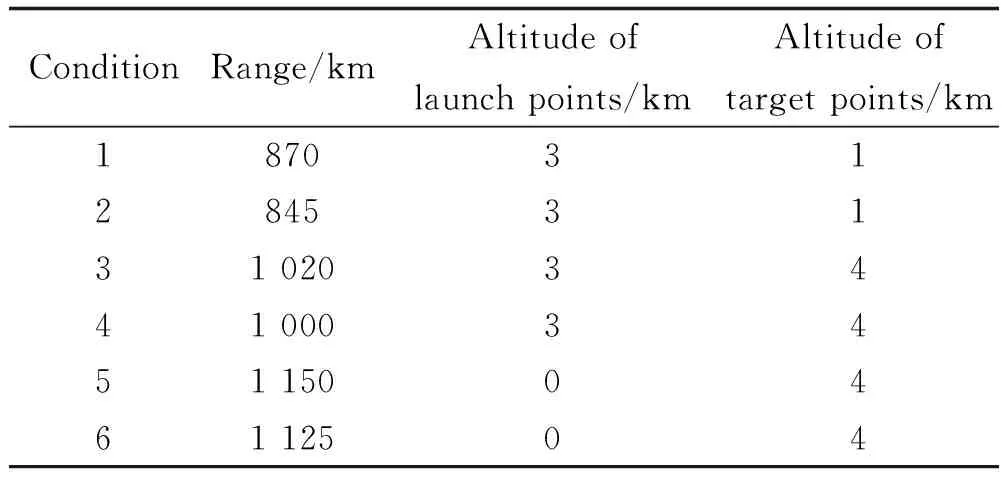
表1 發(fā)射點(diǎn)、目標(biāo)點(diǎn)條件設(shè)置Table 1 Conditions of launch points and target points

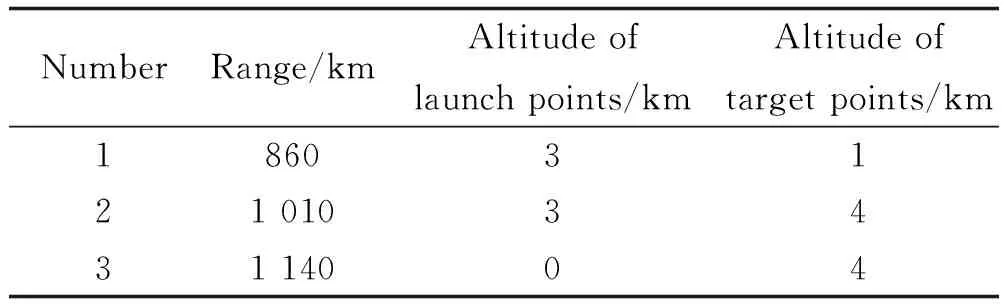
表2 基準(zhǔn)彈道Table 2 Reference trajectories

利用存儲(chǔ)的具有樹形結(jié)構(gòu)的網(wǎng)格化彈道,采用二次規(guī)劃對(duì)分段多項(xiàng)式的基準(zhǔn)彈道進(jìn)行還原。還原后的彈道與離線設(shè)計(jì)的基準(zhǔn)彈道的對(duì)比如圖1所示。從圖中可以看出,還原后的彈道在滿足平滑、連續(xù)的基礎(chǔ)上,與對(duì)應(yīng)的基準(zhǔn)彈道非常接近,較好地反映了原始彈道的形態(tài)。

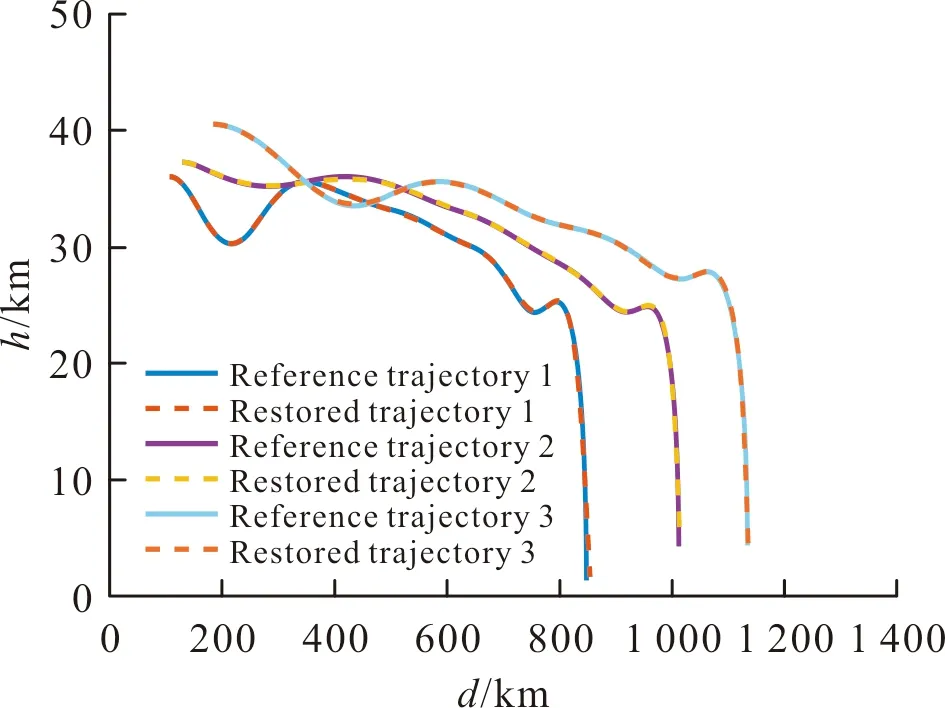
圖1 還原后彈道與基準(zhǔn)彈道對(duì)比Fig.1 Comparison of restored trajectories and reference trajectories

利用還原得到的彈道,可以計(jì)算控制指令,并根據(jù)各個(gè)條件下彈道終點(diǎn)與目標(biāo)點(diǎn)位置的差,建立二次規(guī)劃問題,進(jìn)行控制指令的修正,以完成彈道的在線優(yōu)化。由于基準(zhǔn)彈道的射程與期望射程具有一定的差距,一般需要多次迭代才能使彈道目標(biāo)點(diǎn)附近。在MATLAB平臺(tái)的仿真中,彈道的規(guī)劃需用時(shí)間約為數(shù)十秒,且主要消耗在二次規(guī)劃的求解過程。圖2～圖7為最終優(yōu)化得到的不同條件下的彈道形式與攻角的變化情況。從圖中可以看出,對(duì)于不同條件,控制指令的修正使攻角產(chǎn)生較大差距,彈道形式也發(fā)生較大變化,但都能到達(dá)對(duì)應(yīng)的目標(biāo)點(diǎn)附近,優(yōu)化效果較好。

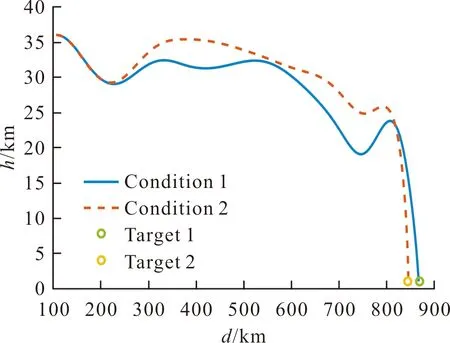
圖2 條件1、條件2下優(yōu)化后的彈道形式Fig.2 Optimized trajectories under condition 1 and condition 2

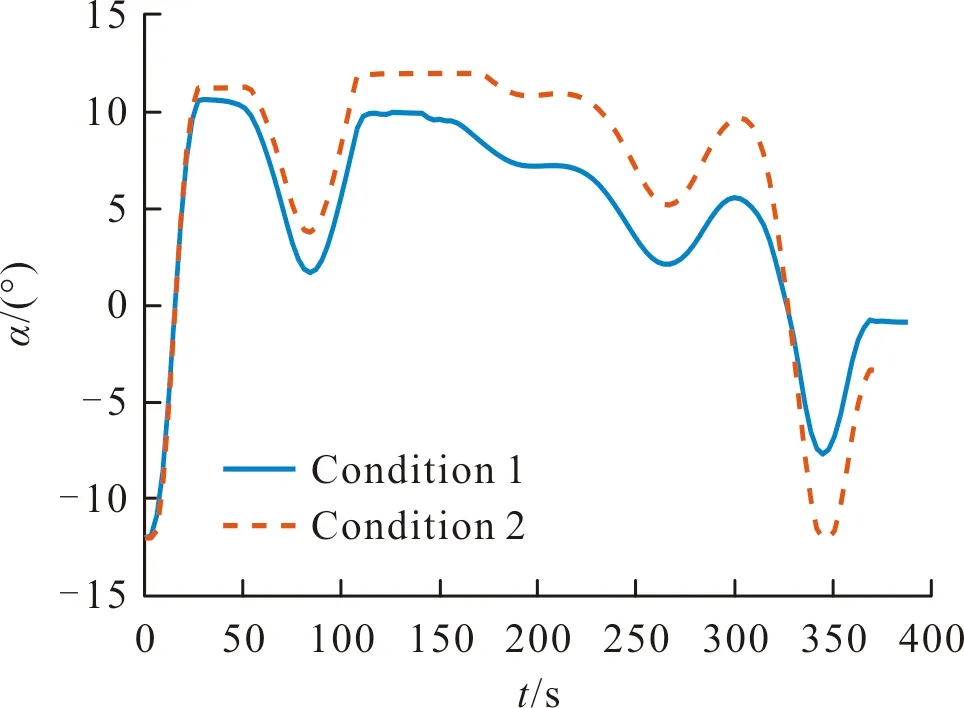
圖3 條件1、條件2下優(yōu)化后的攻角形式Fig.3 AOA after optimization under condition 1 and condition 2

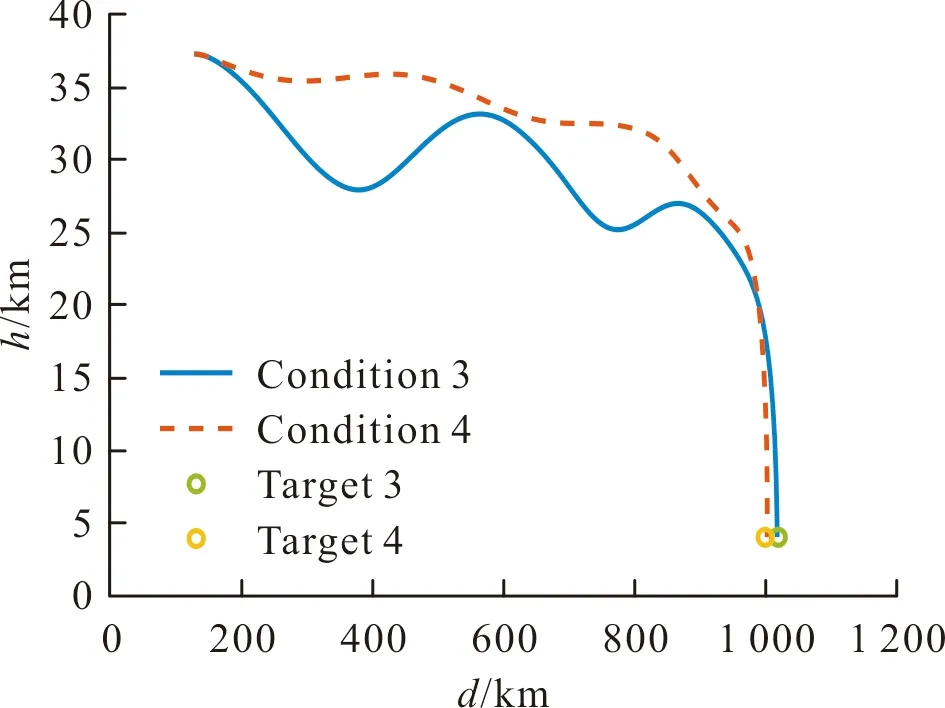
圖4 條件3、條件4下優(yōu)化后的彈道形式Fig.4 Optimized trajectories under condition 3 and condition 4

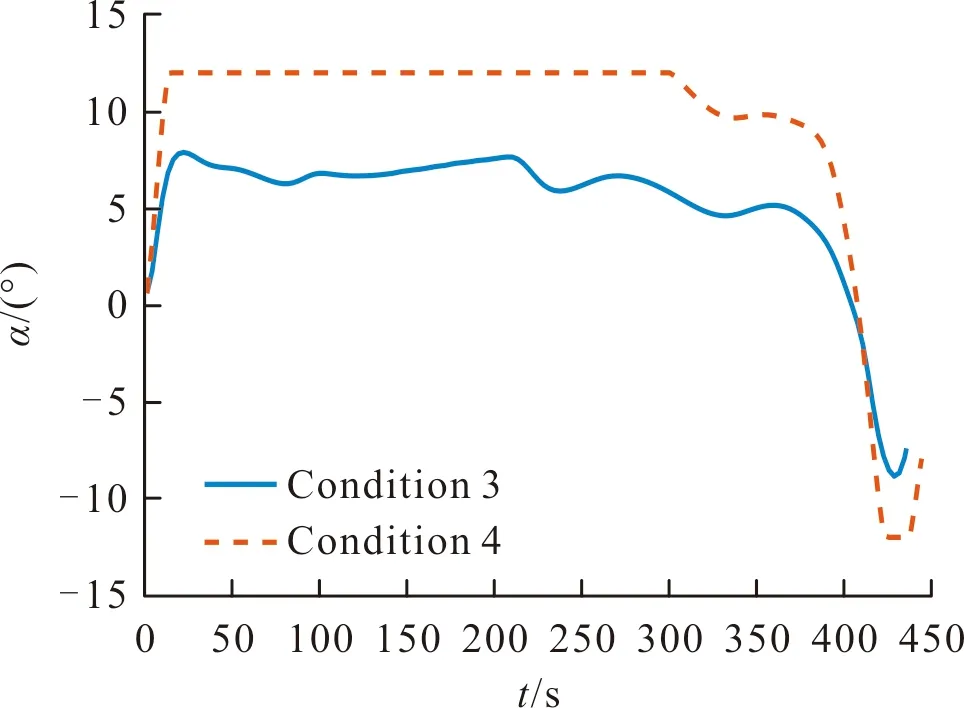
圖5 條件3、條件4下優(yōu)化后的攻角形式Fig.5 AOA after optimization under condition 3 and condition 4

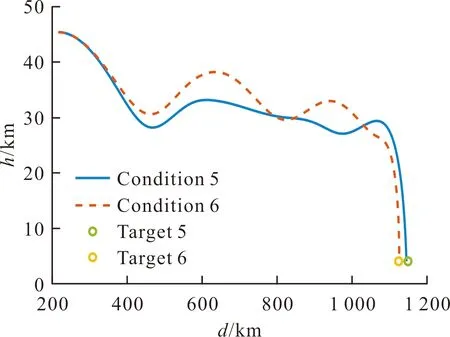
圖6 條件5、條件6下優(yōu)化后的彈道形式Fig.6 Optimized trajectories under condition 5 and condition 6

圖7 條件5、條件6下優(yōu)化后的攻角形式Fig.7 AOA after optimization under condition 5 and condition 6

4 結(jié)論

文中設(shè)計(jì)了一種在線彈道規(guī)劃的方法,以網(wǎng)格化、樹形結(jié)構(gòu)存儲(chǔ)的離線設(shè)計(jì)的彈道為基礎(chǔ),通過構(gòu)建并求解二次規(guī)劃問題,利用分段多項(xiàng)式形式對(duì)彈道進(jìn)行還原,并通過預(yù)測校正法,根據(jù)積分獲得的彈道終點(diǎn)與目標(biāo)點(diǎn)的偏差,并再次建立二次規(guī)劃以求取控制量的修正量,利用多次迭代使彈道達(dá)到目標(biāo)點(diǎn)附近。通過MATLAB平臺(tái)上的仿真驗(yàn)證,得到如下結(jié)論:

1)樹形結(jié)構(gòu)存儲(chǔ)的網(wǎng)格化彈道能夠大大減小數(shù)據(jù)存儲(chǔ)量;

2)分段多項(xiàng)式具有較強(qiáng)的擬合能力,對(duì)各種形式的彈道都有較好的擬合效果;

3)利用預(yù)測校正法,通過構(gòu)建并求解二次規(guī)劃問題,能夠在滿足攻角約束的情況下,獲取平滑、具有高階連續(xù)性的彈道,通過積分可進(jìn)一步使彈道滿足微分約束;

4)應(yīng)用該方法時(shí)的計(jì)算量主要產(chǎn)生在二次規(guī)劃問題的求解過程,且彈道終點(diǎn)與目標(biāo)點(diǎn)越接近,求解需用時(shí)間越短。