直升機載主動攔截防御系統彈目交會概率仿真

李 雪，魏靖彪，李引良，李建偉

(1 陸軍航空兵學院，北京 101121；2 陸軍航空兵研究所，北京 101121；3 西安現代控制技術研究所，陜西 西安 710065)

0 引言

直升機擔負著對地打擊、空中支援、爭奪低空/超低空制空權等多種任務,戰場環境惡劣。典型作戰環境中,由于直升機飛行高度低、防護裝甲能力弱、紅外輻射較強,易受到便攜式防空導彈(man-portable air-defence system,MANPADS)、近距空空導彈和火箭助推榴彈(rocket propelled grenade,RPG)的攻擊。現有的直升機防護手段側重干擾和誘騙,即“軟殺傷”,對MANPADS、近距空空導彈的防護效果有限,對近距突襲的非制導RPG則完全沒有防護能力。

直升機主動攔截防護技術是一種硬殺傷防護手段,通過對來襲彈藥的精確探測和火控解算,適時發射小型攔截彈,在飛離直升機一定距離處起爆,形成定向高速毀傷元,對MANPADS、近距空空導彈和RPG等目標進行高效攔截毀傷。該項技術主要應用于陸軍航空兵部隊的武裝直升機和運輸直升機,可大幅提升直升機在惡劣戰場環境下的生存能力。

主動攔截防護技術首先在裝甲車輛平臺上得到應用。雷灝等[1]介紹了國外裝甲車輛主動防護系統的發展情況和現狀,總結了國外裝甲車輛主動防護系統的主要發展趨勢。李建偉[2]對硬殺傷型坦克主動防護系統的攔截概率進行研究。薛增全等[3]提出了一種基于交會率和攔截效能的最佳設計方法,經驗證能夠滿足主動防護系統最佳攔截區域設計的需要。

隨著地面裝甲車輛平臺上主動防護技術的成熟和發展,西方軍事強國逐漸發展空中平臺的主動防護技術。2012年以色列拉法爾公司成功進行了直升機硬殺傷主動防護測試[4]。2014年,Chapman等[5]提出了下一代飛機防護系統對抗先進MANPADS的技術。美國阿聯特軌道公司2014年完成了直升機主動防護關鍵技術測試[6]。2017年美國提出了隱身戰機動能主動防御新概念[7]。

在國內,隨著反恐和低強度作戰模式成為常態,諶廣昌等[8]探討了軍用直升機作戰環境下的威脅類型,總結了現有軍用裝備RPG主被動防護技術與軍用直升機的適用匹配性,提出了軍用直升機RPG主動防護技術未來需求和研究方向。初步研究表明:對于專用武裝直升機,最佳生存策略是采取迅猛機動方式規避;對于運輸直升機,較為合理的對抗方案是采取動能攔截硬殺傷。史志富[9]提出,軍用直升機的主動防御技術是未來提高軍用直升機戰場生存力的創新性前沿技術。陳黎[10]針對國外運轟機主動防護技術的發展進行了分析,對未來運轟機主動防護的可能技術方案進行了預測。

李冬等[11]應用排隊論建立了防空導彈武器系統攻擊毀傷模型,以傳統概率論為基礎,對防空導系統攔截低小慢無人機集群進行了效能分析。張高峰等[12]采用蒙特卡洛方法建立了艦空導彈對反艦導彈目標的攔截效能模型。利用Matlab對模型進行了程序實現,完成了艦空導彈對不同突防條件下的反艦導彈的攔截效能分析。文中按照直升機載主動攔截防御系統流程,將攔截火箭彈作用分為二維伺服調轉到位、攔截火箭彈發射、飛行、近感引信作用、彈目交會等過程。針對作用過程中的各項參數,建立了攔截火箭彈與來襲彈藥交會過程仿真模型。通過仿真計算,分析了系統中各誤差對交會概率的影響。結果表明:雷達測距誤差和測速誤差對交會概率無顯著影響,雷達測角誤差、伺服調轉誤差和立靶密集度[13]對彈目交會概率有顯著影響。研究可對全系統指標分配和參數優化提供指導。

1 工作原理

直升機載主動攔截防御系統作戰使用時一般與機載告警系統聯合工作,如圖1所示。在告警系統發現來襲威脅目標后,快速啟動探測雷達,探測雷達對防御區域進行搜索,發現來襲目標后進行識別跟蹤,并將目標數據發送至綜合控制箱,進行目標數據濾波、擬合、預測,根據預測的目標航跡確認是否構成威脅;若構成威脅,則實時解算最佳攔截位置、伺服調轉角度及發射時刻,二維隨動裝置根據指令進行方位和俯仰快速調轉,對準解算的最佳位置,當滿足發射條件,綜合控制箱發送發射指令,攔截彈點火發射,沿預定彈道穩定飛行,彈上敏感器對周向空間進行探測,識別目標后適時起爆戰斗部,形成高速毀傷元毀傷來襲目標,未發現目標則自毀。

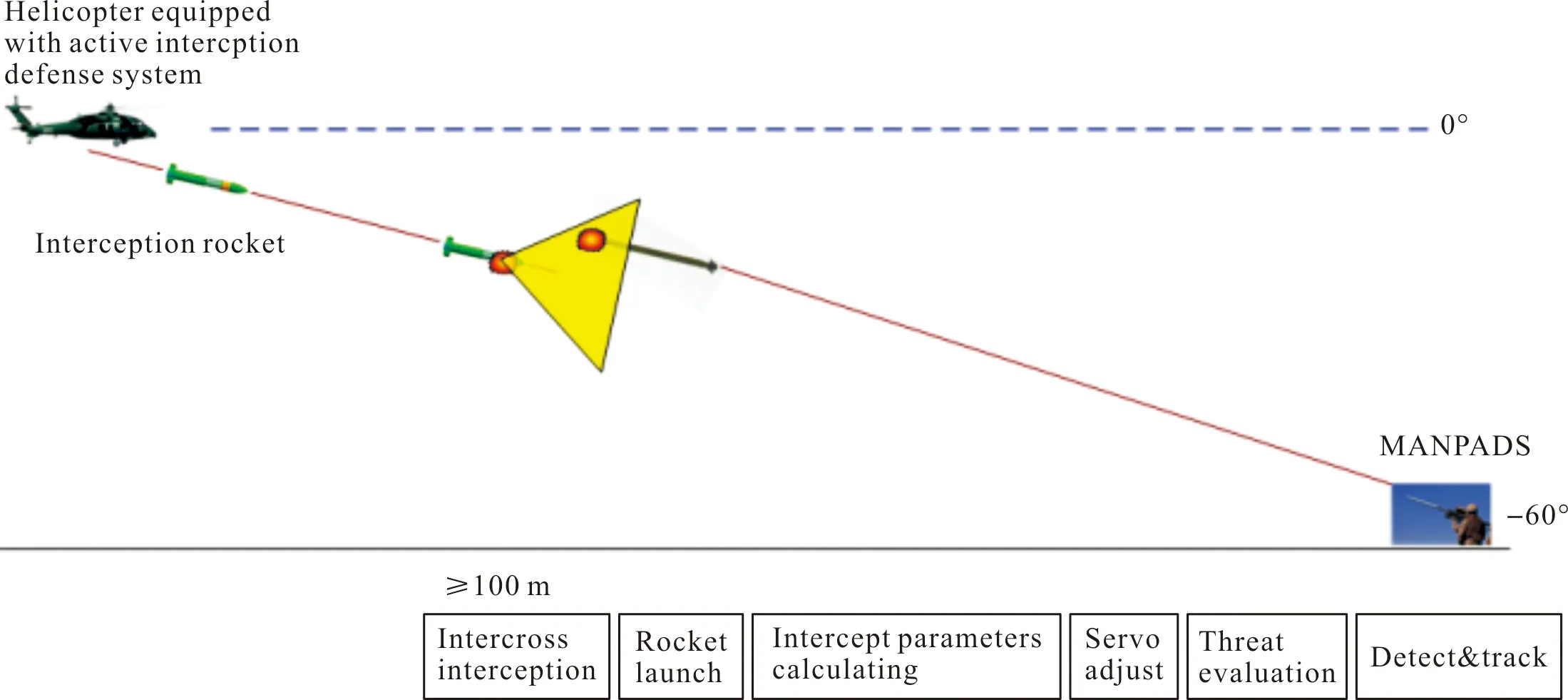
圖1 直升機載主動攔截防御系統作戰工作原理Fig.1 Principle of active interception defense system of helicopter

2 計算模型

2.1 來襲彈藥

2.1.1 特征及基本假設

直升機載主動攔截防御系統的典型攔截對象為MANPADS和RPG,其主要特征如表1所示。

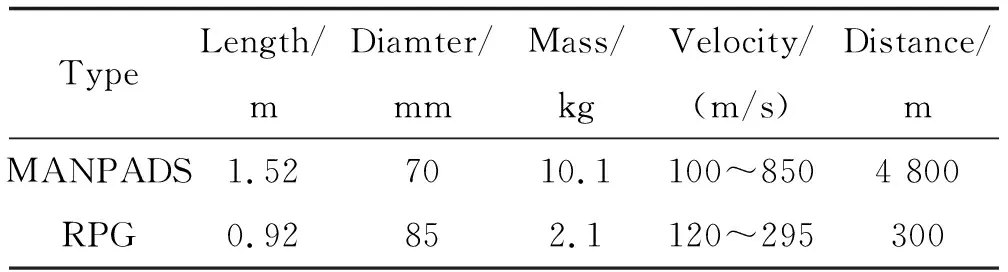
表1 MANPADS和RPG特征Table 1 Parameters of MANPADS and RPG

2.1.2 來襲彈藥基本假設

為了能夠對直升機主動防護系統的攔截效能進行準確的仿真評估,需要提供一種假想的來襲彈藥,該彈藥應能夠反映絕大多數來襲目標的外形及運動特征。

假定來襲彈藥參數:初始速度為100～850 m/s;彈藥類型:MANPADS,速度為Ma2.2,RPG速度為120～295 m/s;彈藥尺寸:圓柱體Φ70 mm×1 520 mm和Φ90 mm×920 mm;飛行模式為勻加速直線運動;運動路線為起點與終點的連線。

2.2 數據處理

根據系統工作原理,仿真模型主要包括流程為:

1)生成來襲彈藥理論航跡;

2)生成雷達量測數據;

3)測量數據的平滑擬合;

4)二維伺服調轉角數據平滑擬合;

5)航跡用數據的平滑及擬合;

6)調轉角與航跡預測;

7)威脅、截止時刻判斷及攔截參數解算;

8)伺服調轉、攔截火箭彈發射;

9)攔截火箭彈飛行、彈目交會、攔截毀傷。

2.3 攔截火箭彈模塊

攔截火箭彈運動起點參數為:

(1)

(2)

式中:函數randn(1)是產生服從均值為0、方差為1的正態分布的隨機數;函數arctan 2(y,x)返回以弧度表示的y/x的反正切。

火箭彈發射時刻射向為:θ0=θi+Δθ1,φ0=φi+Δφ1。角度φi、θi為二維伺服調轉角,Δφ1、Δθ1為二維伺服調轉角誤差,其值在±5 mil內均勻分布的隨機數。

火箭彈起點坐標為(0,0,0),運動方向數為:

(3)

在系統坐標系內,任意時刻ti攔截火箭彈的位置坐標為:

(4)

式中:V為來襲目標速度;a為來襲目標加速度。已知任意時刻來襲彈藥的位置和攔截火箭彈的位置,兩者的位置關系即可判斷交會過程。

2.4 彈目交會模塊

探測截止點是指在系統作用過程中雷達對來襲目標停止探測的時刻來襲目標的位置。探測截止點之后雷達的探測數據,對于系統來說已經來不及做出攔截反應,因此該時刻停止雷達探測。

彈目交會過程是計算從探測截至點時刻開始,來襲彈藥真實航跡與敏感火箭彈是否能夠交會。

坐標系旋轉過程:繞Z軸線轉方位角-θ,再繞X軸旋轉俯仰角φ,使得Y′與Y重合。系統坐標系經過俯仰角和方位角的旋轉后,轉換為攔截火箭發射坐標系,火箭彈發射方向與Y′軸重合,如圖2所示。同時,將探測截至點時刻開始,來襲彈藥真實航跡在系統坐標系下的位置轉換到攔截火箭彈坐標系。坐標轉換公式為:

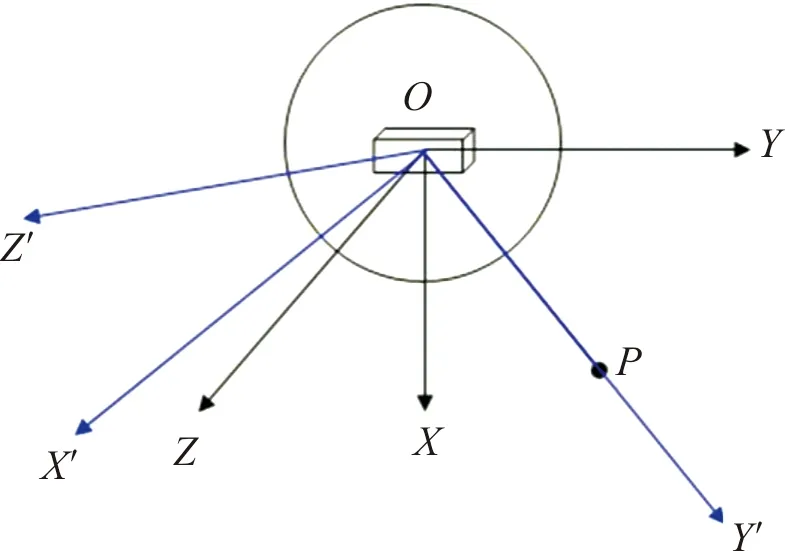
圖2 系統坐標旋轉到攔截火箭坐標系Fig.2 The system coordinate rotates to the interceptor rocket coordinate system

(5)

在交會模型中,根據戰斗部和引信的類型,存在兩種交會情況:一種是來襲彈藥與前向引信交會;另一種是來襲彈藥與周向引信交會。如圖3、圖4所示。圖4中,Lq為引信前向探測距離,α1為前向波束角,Lz為引信周向探測距離,α2為周向波束角,α3為周向引信前傾角,Ld為攔截火箭彈長度,Lm為MANPADS長度;Lr為RPG長度;Dz為攔截火箭彈直徑。

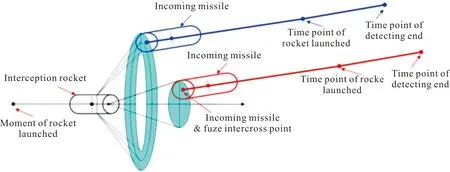
圖3 彈目交會示意圖Fig.3 Intercrossing schematic diagram of missile-target

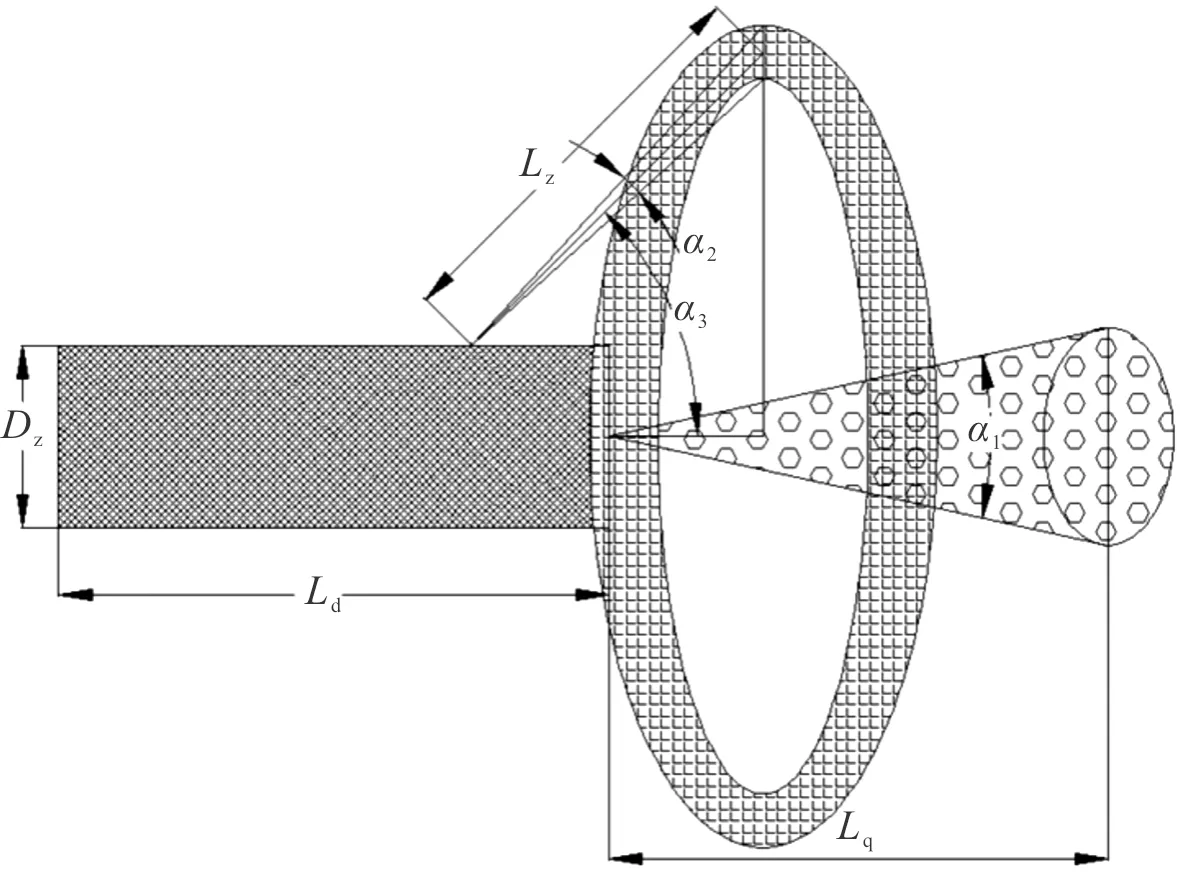
圖4 攔截火箭彈示意圖Fig.4 Schematic diagram of intercepting rocket

交會過程計算:

(6)

式中R0為表示戰斗部的作用距離,一般取值為20 m。

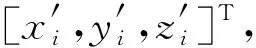
(7)

火箭彈沿著Y軸飛行,前向引信和周向引信探測區域形成一個垂直于Y軸的平面,該平面方程為(參數用xq,yq,zq表示):

(8)

對于前向引信平面方程,通過實時聯立解算引信平面式(8)與來襲彈藥運動直線式(7),可得來襲彈藥與引信探測區域的交會點坐標(xqjh,yqjh,zqjh)。

(9)

周向引信圓錐面方程(參數用xq,yq,zq表示):

(10)

對于周向引信圓錐面方程,通過實時聯立解算引信圓錐面式(10)與來襲彈藥運動直線式(7),可得來襲彈藥與引信探測區域的交會點坐標(xzjh,yzjh,zzjh)。

對于周向引信圓錐面面方程,假設:

(11)

(12)

(13)

(14)

(15)

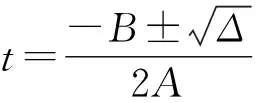
(16)

若Δ<0,t無實數解,則沿當前真實航跡飛行不構成威脅。

聯立解算式(7)、式(10)得到交會點坐標(xzjh,yzjh,zzjh),坐標為:

(17)

對于前向引信,目標速度Ma數>1時,當滿足:

(18)

表示交會點在前向引信的探測區域內且火箭彈攔截距離在200 m之外,判定攔截彈與來襲目標交會成功;目標速度馬赫數≤1時,當滿足:

(19)

表示交會點在前向引信的探測區域內且火箭彈攔截距離在100 m之外,判定攔截彈與來襲目標交會成功。

對于周向引信,R1=7 m,目標速度馬赫數>1時,當滿足:

(20)

表示交會點在周向引信的探測區域內且火箭彈攔截距離在200 m之外,判定攔截彈與來襲目標交會成功;目標速度馬赫數<1時,當滿足:

(21)

表示交會點在周向引信的探測區域內且火箭彈攔截距離在100 m之外,判定攔截彈與來襲目標交會成功。

3 交會概率仿真計算結果

3.1 標準計算條件

1) 攔截距離:100 m;

2) 攔截火箭彈初始速度:150 m/s;

3) 攔截火箭彈加速度:600 m/s2;

4) 系統攔截半徑:10 m;

5) 二維伺服調轉時間(粗調轉):0.5 s;

6) 二維伺服調轉時間(精調轉): 0.3 s;

7) 雷達采樣周期:0.5 ms;

8) 雷達測距誤差Er:≤0.25 m;

9) 雷達測角誤差Eθ:≤0.1°;

10) 雷達測速誤差Ev:≤1%;

11) 雷達探測距離:≥3 000 m;

12) 伺服調轉誤差E?:≤5 mil。

3.2 仿真計算結果

以標準計算條件為約束條件,依據先前的計算模型,完成一次對來襲彈藥的仿真攔截。如果攔截彈與來襲目標交會成功,記為Pn=1,否則記為Pn=0,其中n表示第n次仿真。假設仿真次數為N(N為正整數),那么N次仿真后交會概率P為:

(22)

設定雷達測距誤差為Er、測角誤差為Eθ、測速誤差為Ev、伺服調轉誤差為E?等參數變量,仿真計算交會概率為P,如表2～表7所示。

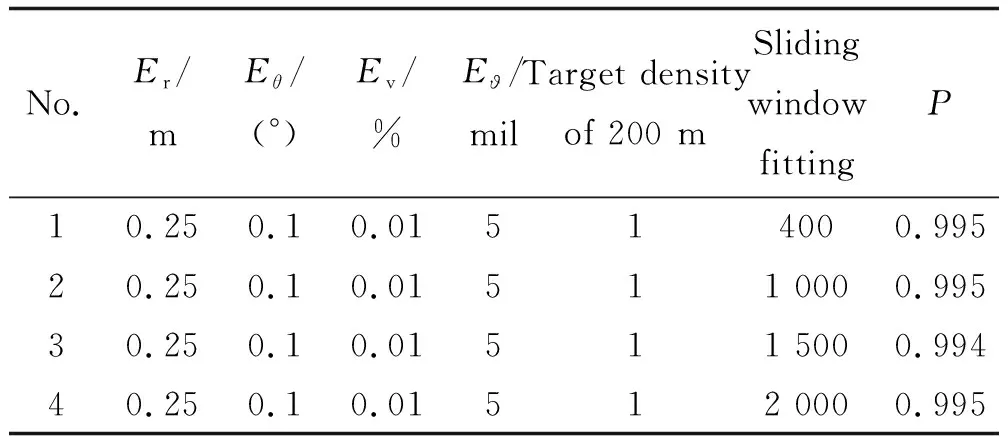
表2 滑窗擬合用數據量對交會概率的影響Table 2 The influence of data amount of sliding window fitting on intercross probability

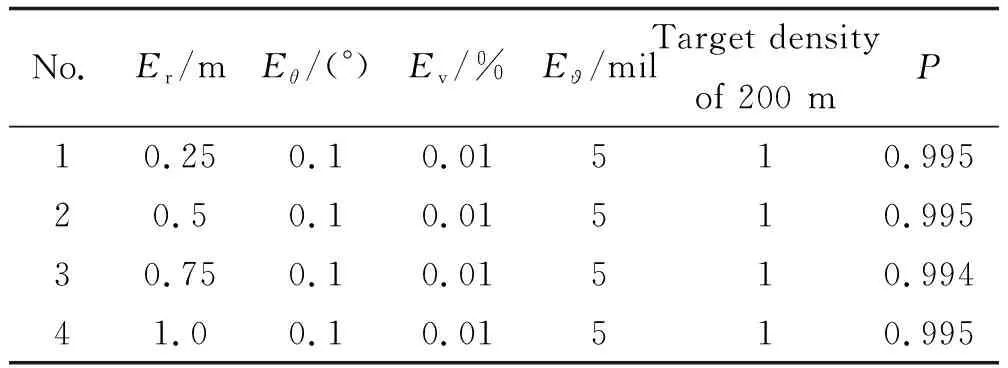
表3 雷達探測距離誤差對交會概率的影響Table 3 The influence of radar detection range error on intercross probability

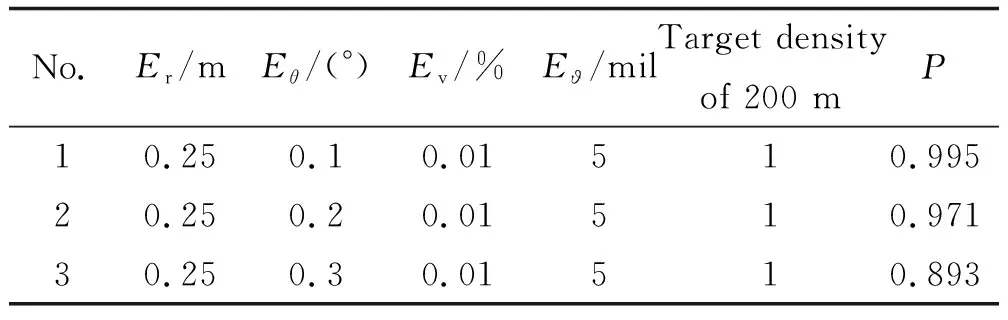
表4 雷達探測角度誤差對交會概率的影響Table 4 The influence of radar detection angle error on intercross probability

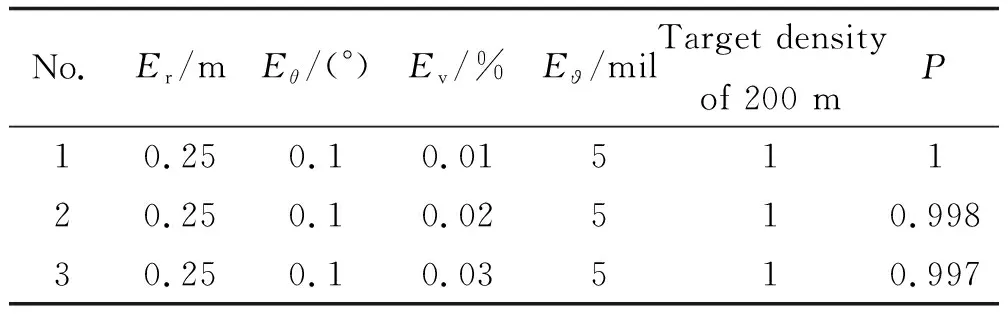
表5 雷達探測速度誤差對交會概率的影響Table 5 The influence of radar detection velocity error on intercross probability

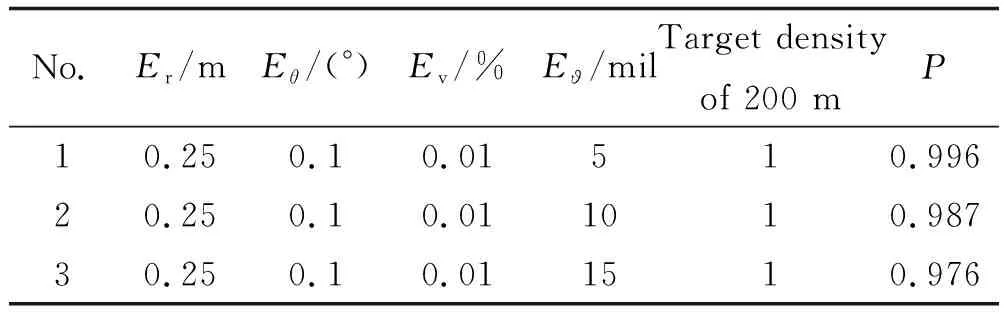
表6 伺服調轉誤差對交會概率的影響Table 6 The influence of servo rotation error on intercross probability

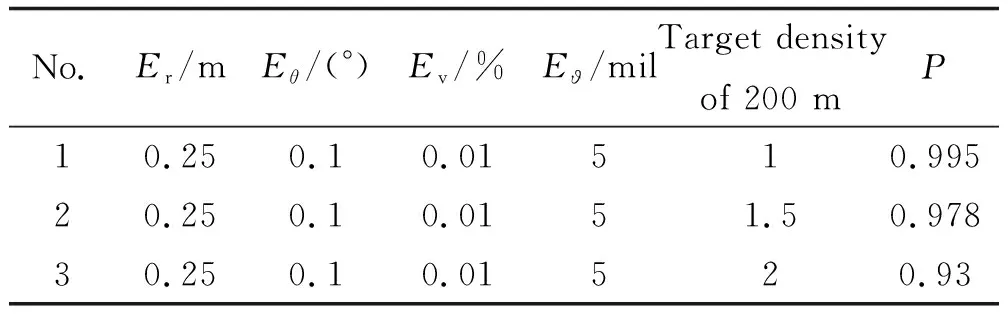
表7 立靶密集度對交會概率的影響Table 7 The influence of vertical dispersion density on intercross probability

3.3 仿真結果分析

1)擬合數據量N≥400可以滿足要求,對交會概率無顯著影響。

2)雷達測距誤差和測速誤差對交會概率、前向交會概率和周向交會概率無影響。

3)雷達測角誤差對交會概率、前向交會概率和周向交會概率均有影響。測角誤差增大3倍,交會概率下降約10%。測角誤差增大,前向交會概率減小,周向交會概率增大。測角誤差對前向交會概率的影響比對周向交會概率的影響更顯著。

4)伺服調轉角誤差增大1倍,交會概率下降約1%。伺服調轉誤差增大,前向交會概率減小,周向交會概率增大。伺服調轉角誤差增大,前向交會概率減小,周向交會概率增大。

5)立靶密集度增大1倍,交會概率下降約6%。立靶密集度增大,前向交會概率減小,周向交會概率增大。

4 結論

通過系統研究,得出以下主要結論:

1)雷達測距誤差和測速誤差對交會概率無顯著影響,該指標可適當放寬。

2)雷達測角誤差、伺服調轉誤差和立靶密集度對交會概率有顯著影響。測角誤差增大3倍,交會概率下降10%;伺服調轉誤差增大1倍,交會概率下降1%;立靶密集度增大1倍,交會概率下降6%。