基于仿冰壺火炬傳遞機器人的全向輪運動設計研究

王福利，陸洋

（1.中國科學院 沈陽自動化研究所，沈陽 110016；2.中國科學院 機器人與智能制造創新研究院，沈陽 110169）

0 引言

移動機器人是機器人領域的移動機構的一個重要組成部分，被廣泛研究。按照移動方式，移動機器人被分為輪式、履帶式、腿式、爬行式、跳躍式及復合式。而輪式移動機器人具有結構簡單、運動建模容易、成本低、對場地要求低、運動靈活、穩定性和可靠性高等優點，被廣泛應用。

根據移動特性，移動機器人分為全向移動機器人和非全向移動機器人[1]。當移動機器人同時具有前后、左右、旋轉3個自由度時，則被稱為全向移動機器人。不能同時具有3個自由度或者少于3個自由度的移動機器人則被稱為非全向移動機器人。全向移動機器人克服了普通移動機器不能在3個自由度之間隨意切換而帶來的非完整性約束，能夠在平面實現橫移、斜移、旋轉甚至更復雜的運動，實現全方位運動[2-3]。

全向輪是一種具有3個自由度的特殊輪子，一般由輪轂和從動輪組成，通過多個全向輪的組合，可以使機器人實現全向移動。這種由全向輪組成的全向移動機器人具有較好的機動性、靈活性等特點，逐漸成為全向移動機器人移動機構的主流。

全向移動平臺作為全向移動機器人的運動執行部分，有著較為完整的體系和擴展性。它能夠根據不同的應用場景搭載不同的移動輪組和不同的結構布局，實現不同的功能要求。

本文所設計的仿冰壺火炬傳遞機器人，由于實際傳遞場景運動曲線特性的特殊性（像冰壺一樣，旋轉的同時完成前進動作），如圖1所示，對機器人的全向移動平臺運動性能要求較高，對系統的加速度、速度、角速度等運動性能的物理量不斷調整，使得機器人的運動性能始終為最優性能。

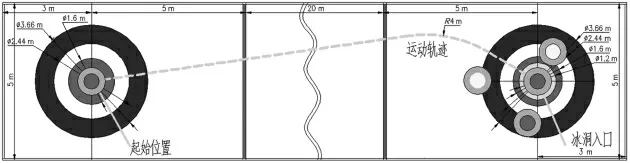
圖1 機器人運行場景

1 全向移動平臺設計與研究

1.1 全向輪的選擇

全向輪作為全移動平臺的運動執行機構的重要組成部分，其選擇十分重要。全向輪是一種特殊的輪系，其特點是沿主輪轂圓周排布著與輪子成一定角度且可繞自身軸線進行旋轉的從動輥子。根據從動輪組與主動輪轂平面角度不同，分為麥克納姆輪和OMIN全向輪。麥克納姆輪的從動輥輪相對于車輪平面成45°角，相對于穿過滾輪中心的平行于車輪旋轉軸的直線成45°角。而OMIN全向輪則是在主動輪轂外輪廓上均勻分布著沿垂直軸分布的從動輥輪，從動輥輪的軸與輪轂軸正交[4]，如圖2所示。

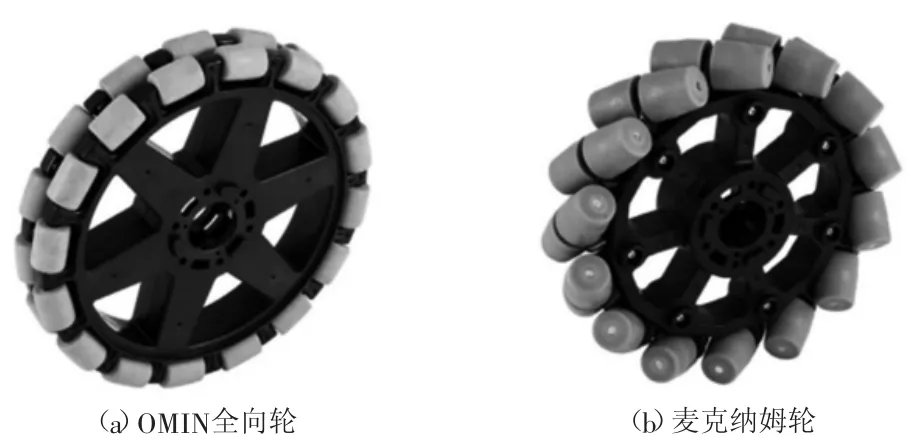
圖2 全向輪示意圖

麥克納姆輪的優點為：外形美觀，全向移動性能好，承重能力強，與地面摩擦力大、不易打滑。缺點為：加工難（金屬材質較多）、造價高、速度較慢、壽命比傳統膠輪短，每個輪子需要電動機單獨驅動。OMIN全向輪的優點為：結構簡單、易加工、成本低，原地打轉時橫向摩擦力小。缺點為：無法橫向前進，承重能力較弱。兩者還有一個共同的缺點：運動過程中都會橫向卸力。為了保證運動的平穩性，當前一個輥子與地面即將分離時，后一個輥子必須與地面接觸。因此在使用過程中，都選用雙排輪結構的全向輪。

1.2 全向輪運動特性分析

1.2.1 單個全向輪運動特性分析

對于全方位機器人的運動機構，移動平臺通常會通過多個全向輪組合來合成所需要的運動軌跡。不同數量、不同種類的全向輪組合成的運動軌跡是不同的，所以先對單個全向輪進行運動模型分析。

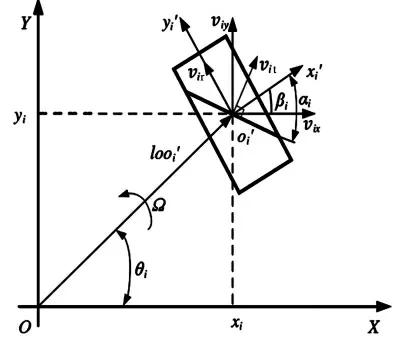
圖3 O-XY坐標系全向輪位置關系

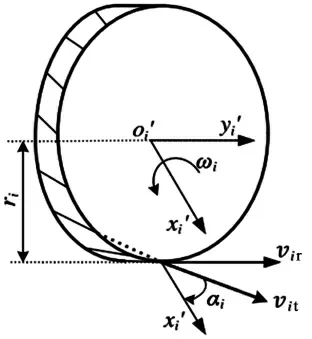
圖4 全向輪坐標系參數位置關系

（xiyiθi）為全向輪本體坐標系到參考坐標系O-XY的位姿；ri為全向輪輪轂半徑，vir為全向輪i沿著輪切線方向與地面的線速度矢量，以圖3箭頭方向為正；vit為輥子轉動時沿著輥子轉動切線方向的線速度矢量，以圖3箭頭方向為正；ωi為全向輪轂的轉動角速度；θi為該全向輪的安裝角，在O-XY坐標系下繞Z軸逆時針方向為正；looi′為全向輪中心oi′在參考坐標系O-XY下的位置矢量，坐標為（xiyi）；Ω為全向輪中心oi′在參考坐標系O-XY下繞Z軸的轉動角速度，繞Z軸逆時針為正。

定義（vxvyΩ）T為參考坐標系O-XY整體運動的廣義速度；（vixvix）T為全向輪中心oi′在坐標系O-XY上的速度矢量；（virvit）T為全向輪坐標系oi′-xi′yi′下的廣義速度，其中vir與ωi滿足如下關系：vir=ri·ωi。

1.2.2 單個全向輪運動方程分析

由圖3可以看出，對于任意角度αi的全向輪，當給定廣義速度（vxvyΩ）T時，通過運動合成，可以得出oi′點在O-XY坐標系下的速度分量（virvit）T，其矢量表達式為

根據式（1），將矢量分解為沿O-XY坐標系下的兩個坐標軸：

將式（2）整理成矩陣形式：

令R1為式（3）從（vxvyΩ）T到（vixviy）T轉換關系的矩陣，可得

定義R2為式（5）從（vixviy）T到（vix′ viy′）T轉換關系的矩陣，可得

定義R3為式（7）從（virvit）T到（vix′ viy′）T轉換關系的矩陣，可得

式（3）、式（5）、式（7）聯合可得（virvit）T與（vxvyΩ）T的關系方程：

式（9）反映了參考系整體的（vxvyΩ）T速度與任意夾角輥子的轉速、切向速度的關系。由det（R2）≠0、det（R3）≠0可得

已知

由式（10）和式（11）整理可得

式中：lx=-looi·sinωiθi、ly=looi·cos θi分別為全向輪到參考坐標系中心X軸和Y軸上的距離。

定義R為式（12）從（vxvyΩ）T到（ωivit）T轉換關系的矩陣，因此

1.2.3 全向輪輪組布局分析

對于全向輪輪組，布局方式是輪的數目、布局的形狀和間距的設計，從根本上講，布局的方式取決于兩種運動模型所組成的輪系雅克比矩陣的奇異性，以及對αi、βi、lx、ly參數數值的選取。當已知多輪系本體上的廣義速度（vxvyΩ）T，為了能夠獲得每個輪所需的轉速（｛ωi|ωi，i=1、2、3、4…｝），需要分析并得到多輪系運動學方程。

由式（13）可得出ωi與廣義速度（vxvyΩ）T的關系為

由式（15）看出，系數矩陣R的列數為3，未知數個數也為4個（αi、βi、lx、ly），故對于全向輪組來說，ωi的個數至少為4。

對于已知αi角度的全向輪，以OMIN全向輪為例，由式（14）可得

由式（16）看出，系數矩陣R的列數為3，未知數個數也為3個（βi、lx、ly），故對于OMNI全向輪來說，ωi的個數至少為3。同理對于45°麥克納姆輪也一樣，ωi的個數至少為3。

1.3 常用全向輪輪系布局分析

對于全向輪組布局結構，國內外學者們進行了大量研究，這里只針對常用的三OMIN全向輪和四麥克納姆輪，以及本機器人采用的四OMIN全向輪進行布局分析[6-7]。

1.3.1 三OMIN全向輪布局分析

建立三OMIN全向輪參考坐標系布局，如圖5所示。

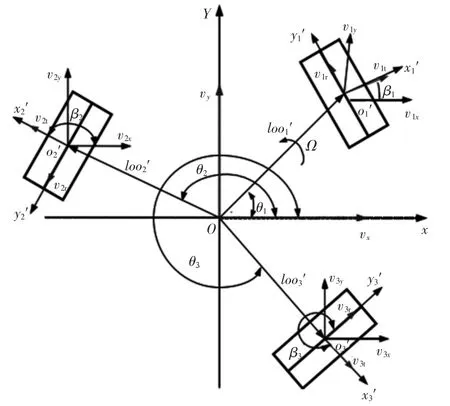
圖5 三OMIN 全向輪坐標系布局

由式（16）得出三輪輪組的運動學方程為

而在最常用的三OMIN全向輪組中，β1=90°，β2=210°，β3=330°，兩兩夾角為120°，θi=βi，且loo1′=loo2′=loo3′=L，各個輪子半徑均為r，如圖6所示。

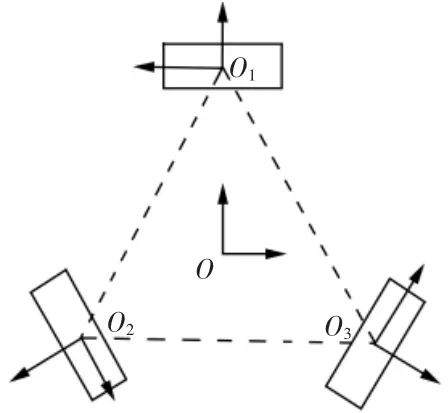
圖6 三OMIN 全向輪正三角布局

簡化后的逆雅可比矩陣為

1.3.2 四OMIN全向輪布局分析

建立三OMIN全向輪參考坐標系布局，如圖7所示.

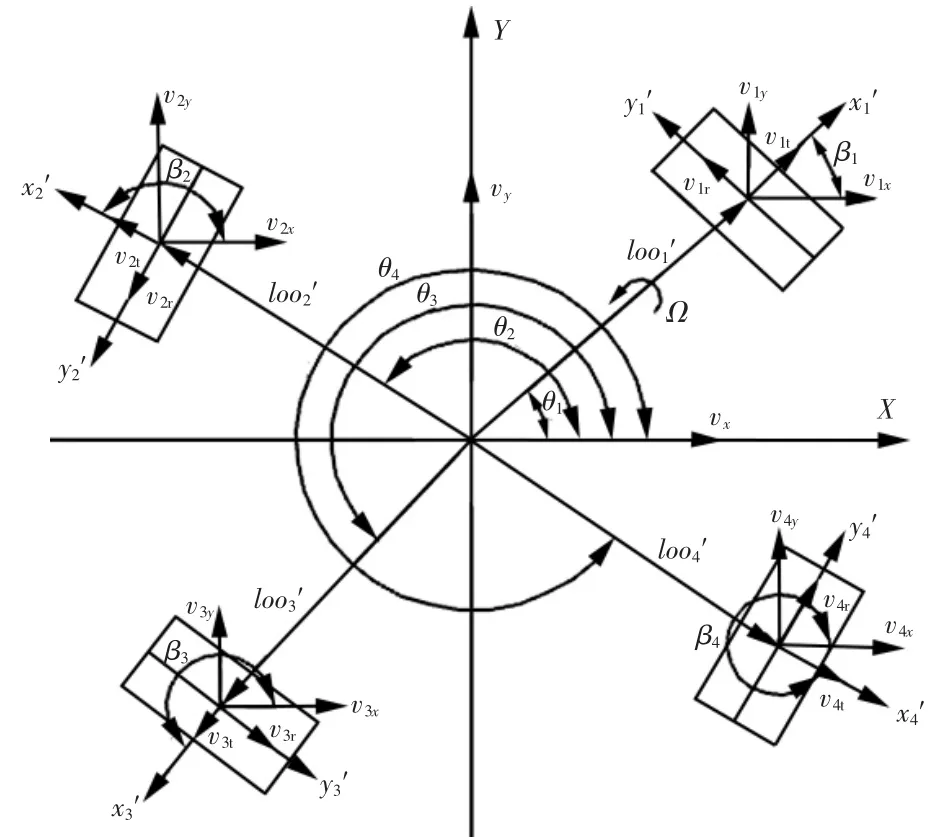
圖7 四OMIN 全向輪坐標系布局

由式（16）得出四輪輪組的運動學方程為

常用布局中OMIN全向輪相對于坐標O-XY相互對稱。根據lx與ly是否相等，可分為方型四角布局、長方形四角布局。對于方形四角布局，β1=45°，β2=135°，β3=225°，β4=315°，兩兩夾角為90°。θi=βi，且loo1′=loo2′=loo3′=loo4′=L，各個輪子半徑均為r。如圖8所示，對應的逆雅可比矩陣為

圖8 四OMIN 全向輪方形四角布局

1.3.3 四麥克納姆輪布局分析

由式（15）得出四麥克納姆輪輪組的運動學方程為

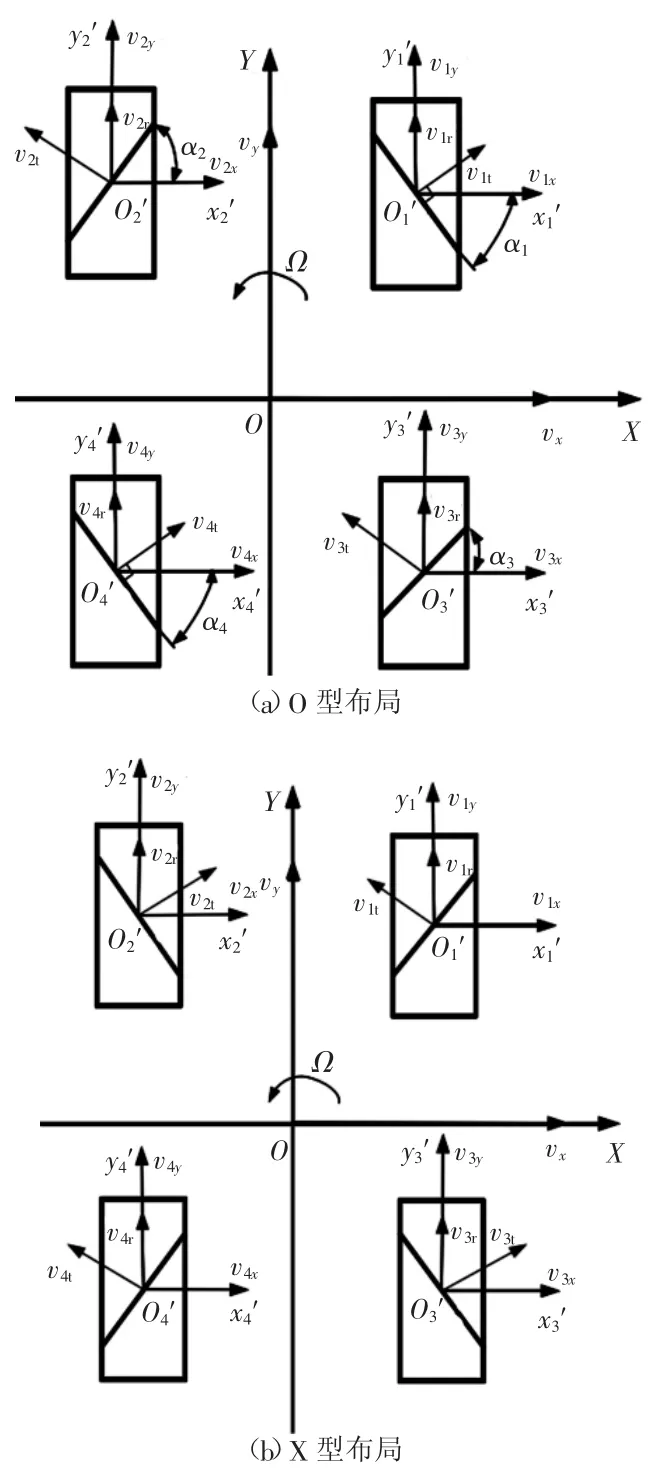
圖9 四麥克納姆輪的兩種布局

對于X型布局，4 個 輪 子 轉動時，沿著Z軸轉動的力臂短，力矩比O型小，通常不使用此方案。由O型布局 圖 可 知，4 個麥克納姆輪半徑一致，即r1=r2=r3=r4=r，并且輪軸彼此平行，輪子安裝方向垂直矩形邊，即β1=β2=β3=β4=0，根據O型布局中的旋向，規定4個麥克納姆輪αi的角度分別為α1=45°，α2=-135°，α3=-135°，α4=45°，且lx1=lx2=lx3=lx4=lx，ly1=ly2=ly3=ly4=ly。簡化后JM4為

1.4 全向輪組的選用

上面分析的3種組合方式，都可以實現全向移動的功能，但是從布局方式上就可以看出很大的差距。

三輪組布局是理論上最簡單的布局方法，具有控制方便、成本低的特點。但是少一個輪子就少了一個驅動電動機，相應的驅動力較小，而且三輪組結構容易造成一個輪子離地，從而導致整體穩定性變差。與之相比，四輪組結構多一個輪子，每個輪子所受的負載也減小。從布局上看，四輪組布局結構對稱，在某一方向的直線移動更加精準，無需傳感器輔助。

單個OMIN全向輪與麥克納姆輪各有優缺點。但是從輪組布局上，四OMIN全向輪布局的旋轉效率更高，而四麥克納姆輪組布局的運動效率更高。全向輪運動的平臺一般要求地面平整，而且有較大的摩擦力。四麥克納姆輪甚至可以在相對復雜的場地上運動[8]。

雖然四麥克納姆輪輪組布局比四OMIN全向輪更有優勢，但是本文涉及的仿冰壺火炬傳遞機器人的外形為圓形的冰壺形狀，且對于機器人的旋轉特性要求要更高一些。另外，冰壺機器人的運動環境主要為冰上運動，為了防止全向輪運動時打滑，需要優先選用摩擦力較大的全向輪。故最終選用四OMIN全向輪布局為全向最終移動平臺，如圖10所示。

圖10 仿冰壺機器人全向輪布局

2 全向輪運動電動機控制設計與研究

電動機控制系統設計是為了實現機器人陸地全方位移動作業，它采用以太網與CAN混合組網的設計方式將各個單元部件聯系在一起。當有大數據傳輸時，各單元之間通信采用以太網通信方式，控制命令與狀態數據反饋則主要采用CAN總線來完成。具體設計的結構如圖11所示。

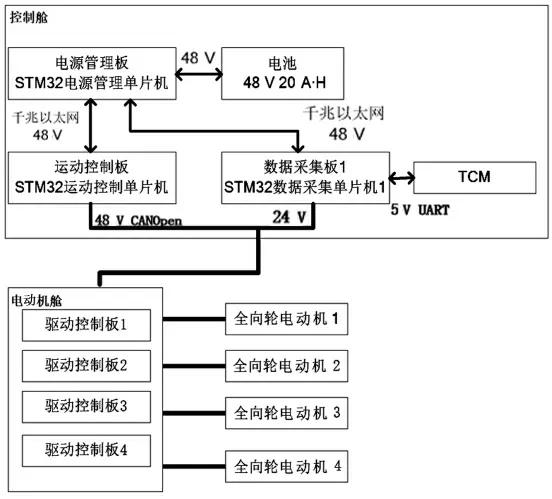
圖11 控制系統結構圖

電源管理單片機管理電池電量并監測能耗，同時為運動控制單片機與數據采集單片機供電并通信。運動控制單片機分別控制電動機艙內的4個驅動控制板，驅動板分別控制全向輪電動機運動，通過速度分解獲得每個車輪輪轂的轉速分量之后，采用矢量控制原理進行全向輪電動機控制，數據采集單片機采集各電動機驅動數據和TCM電子羅盤的數據反饋，通過帶有實時操作系統的DSP實現同步和運動控制，達到期望的運動狀態，如圖12所示。

圖12 火炬傳遞機器人設定軌跡示意圖

依照設定要求，對機器建立了運動學模型觀測，通過試驗測得機器人角速度、艏向角、速度數據，如圖13～圖15所示。

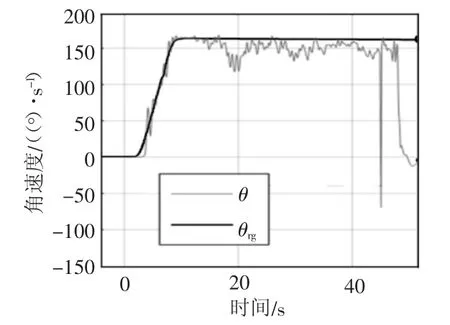
圖13 角速度曲線圖

圖13中灰色線條θ為角速度傳感器陀螺儀測量到的機器人的實時角速度，黑色線條θrg為動力力學模型根據全向輪動力輸出預測的機器人的角速度。可以看出預測角速度都與傳感器測量值差別不大，僅有一些短暫的誤差及一些瞬時的擾動。由圖14可以看出，在機器人運動的過程中，機器人艏向的期望角度與實際角度基本一致，旋轉性能良好，控制準確穩定。圖15中灰色線條v為機器人前進速度，黑色線條vrg為機器人理論前進速度，不難看出機器人均速與理論速度基本吻合，但波動較大、穩定性差，電動機控制效果不夠理想，但不影響機器人達到預期效果。

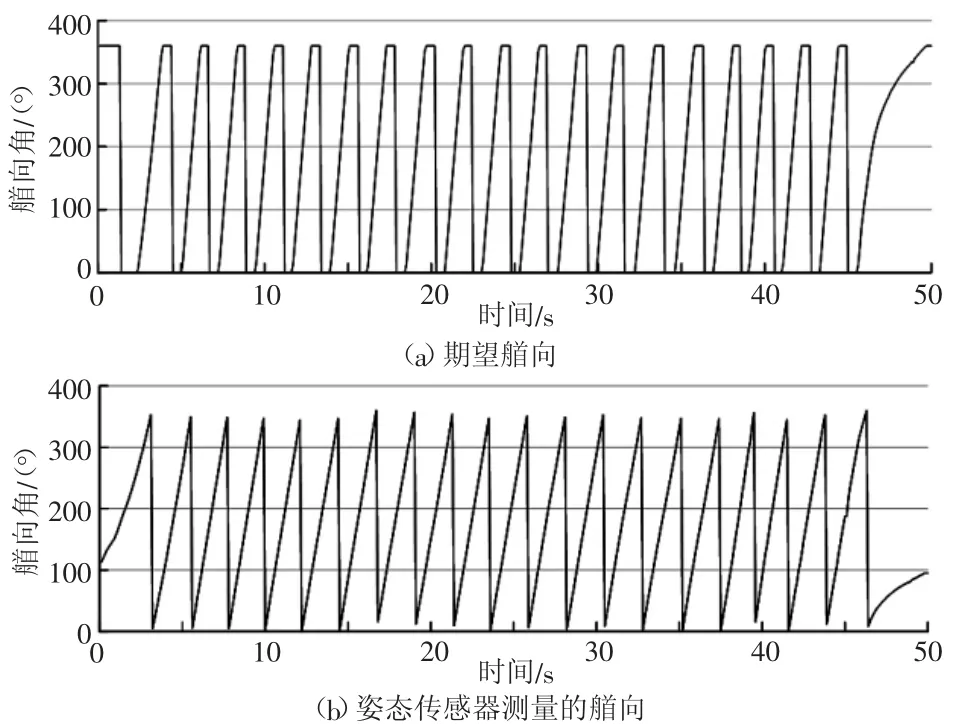
圖14 艏向曲線圖

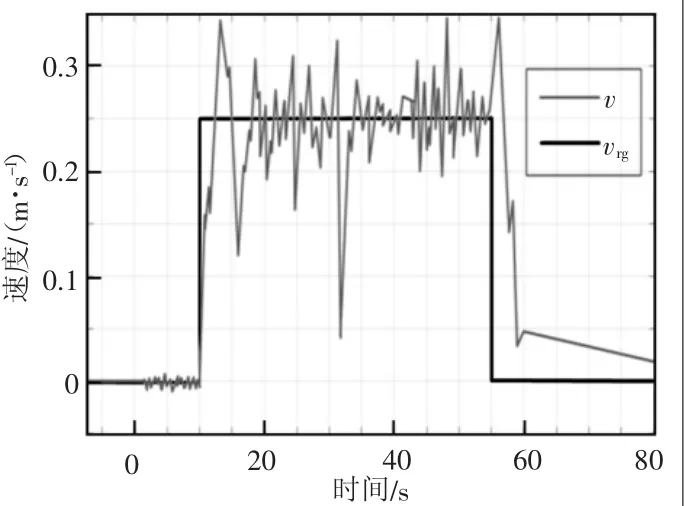
圖15 速度曲線圖

3 結論

在分析2種全向輪的單輪運動特性和多輪組運動特性后，本文綜合分析了它們的優缺點，結合火炬傳遞應用場景設計了四OMIN全向輪移動平臺，該移動平臺實現了火炬傳遞機器人的全方位移動的功能，而且結構簡單，運動控制靈活。充分發揮了其在冰面應用環境下的獨特優點。尤其在冬奧會火炬傳遞距離由最初的50 m縮短到10 m后，充分展現了其高效率的旋轉特性。通過實物成果的展示，驗證了設計理論的合理性及方案的可行性與可靠性。當仿冰壺火炬傳遞機器人手持燃燒火炬，沿冰壺賽道旋轉滑入冰洞口，讓生生不息的奧運圣火階次傳遞，彰顯了奧運與科技的結合。