超深井卡瓦懸掛器套管力學強度有限元分析

練章華 萬智勇 吳彥先 史君林 趙朝陽

(1.西南石油大學油氣藏地質及開發工程國家重點實驗室 2.中國石油新疆油田分公司工程技術研究院)

0 引 言

隨著深井超深井的廣泛開發，大尺寸套管深井越來越多，井口坐掛載荷控制變得困難。坐掛載荷過大會導致井口下沉及卡瓦牙對套管損傷大等問題，過小可能導致套管頭密封性能差等問題。若要避免這些問題，需要對井口卡瓦懸掛器與套管損傷的力學機理進行深入的理論和試驗研究[1-3]。井口裝置作為油井井筒完整性的重要一環，其承壓能力及密封性能直接影響服役狀況下的安全[4-8]，必須進行井口試壓測試。在該過程中往往需要施加較高的壓力，并且在套管軸向載荷以及懸掛器卡瓦夾持力等共同作用下，使得井口位置套管受到較大的復合載荷，極易造成井口管柱變形、損壞等現象，嚴重影響正常作業的安全[9-11]。

目前，關于套管失效方面的研究[12-17]主要集中于地層深處套管在體積壓裂、地層滑移等因素下的失效分析，而有關試壓生產過程中井口套管柱的損傷、斷裂研究相對較少。曾經有學者開展過卡瓦懸掛器套管受力問題理論研究[18-20]，其基本方法是采用靜力學原理對井下封隔器上的卡瓦進行力學分析，得到卡瓦錨定時卡瓦牙的正應力計算公式，但是對于井口坐掛噸位或卡瓦效應的套管拉伸極限載荷方面還缺乏系統的理論研究。而將卡瓦夾持過程中對套管的徑向載荷視為均勻載荷，只能得到套管內壁為塑性失效區，無法計算卡瓦牙吃入套管過程中套管外壁由于應力集中而產生的塑性破壞，并且拉梅公式解析解無法計算套管外壁由于卡瓦牙引起的應力集中，但有限元法能夠解決此問題。為此，筆者將建立套管卡瓦懸掛器有限元計算的3D模型，開展有限元仿真模擬分析，對井口卡瓦式懸掛器中套管的塑性破壞進行安全評價，以期為控制或避免套管斷裂失效提供理論依據和指導，同時也為卡瓦懸掛器套管的設計、各種安全施工作業提供理論依據。

1 懸掛器及套管卡瓦效應極限載荷

目前國內已經多次出現井口套管斷裂情況。圖1為新疆某油田超深井X1井口卡瓦部分高鋼級155V套管斷裂照片。從井口套管斷裂情況以及裂口可知，套管斷裂發生在卡瓦下部，且卡瓦部分套管存在較深的牙痕，裂口還沒有完全斷掉是因為其發生裂紋時被卡瓦抱住，而卡瓦下部沒有被卡瓦抱住的套管則掉入了井中。結合大量現場研究和分析可知，圖1中井口套管斷裂失效的主要原因是卡瓦懸掛器的卡瓦牙在套管外壁產生牙痕，導致套管在懸重作用下產生應力集中，并且在各種作業過程中產生的交變載荷同時作用于該位置，所以卡瓦下部附近套管在過大懸重載荷作用下發生套管縮徑變形，在各種交變載荷作用下，發生井口套管斷裂，同時也有可能是套管質量及服役環境問題，如材質、腐蝕介質、惡劣受力環境等造成的。

圖1 X1井井口卡瓦部分套管斷裂照片Fig.1 Photos of casing failure at slip part of wellhead of Well X1

現場使用的卡瓦式井口套管懸掛器結構如圖2所示，由卡瓦、卡瓦座、密封圈、支撐座以及四通等主要部件組成。

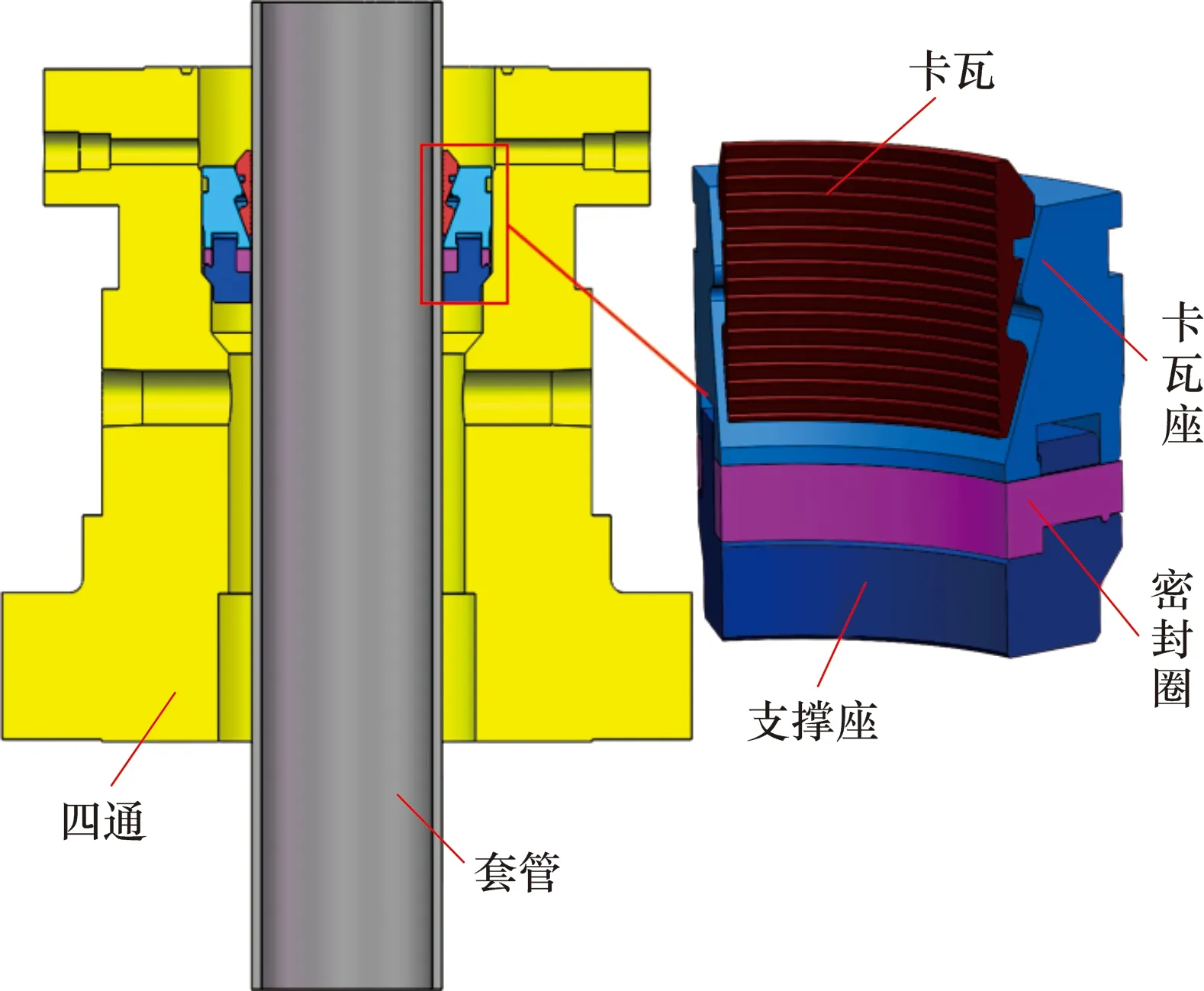
圖2 卡瓦式懸掛器結構示意圖Fig.2 Schematic diagram for structure of slip-type hanger

在卡瓦式懸掛器坐掛過程中，支撐座剛好卡在四通的臺階上，卡瓦座底面通過橡膠密封環和背面與四通接觸實現固定，于是在受力分析時只需要考慮套管、卡瓦和卡瓦座即可。套管頭卡瓦受力如圖3所示。卡瓦咬緊套管是卡瓦與套管柱相互作用受力的過程。卡瓦剛開始咬緊套管時，其主動力來自于卡瓦與套管外壁的初始摩擦力。套管自重和下放沖擊力經錐面傳遞、放大并反作用于卡瓦，使卡瓦將套管徑向抱緊，直到卡瓦不能滑動為止。此時卡瓦與卡瓦座直接通過斜面接觸，套管下落帶動卡瓦微小下滑繼續相互擠壓；但由于卡瓦座位置固定不變，卡瓦牙受擠壓咬入套管，產生一個巨大的擠壓力N2，從而產生足夠的摩擦力，使得套管達到力學平衡。如果套管懸掛載荷繼續增大，則卡瓦會由于受到更大的擠壓力繼續咬入套管，直到達到新的力學平衡狀態。

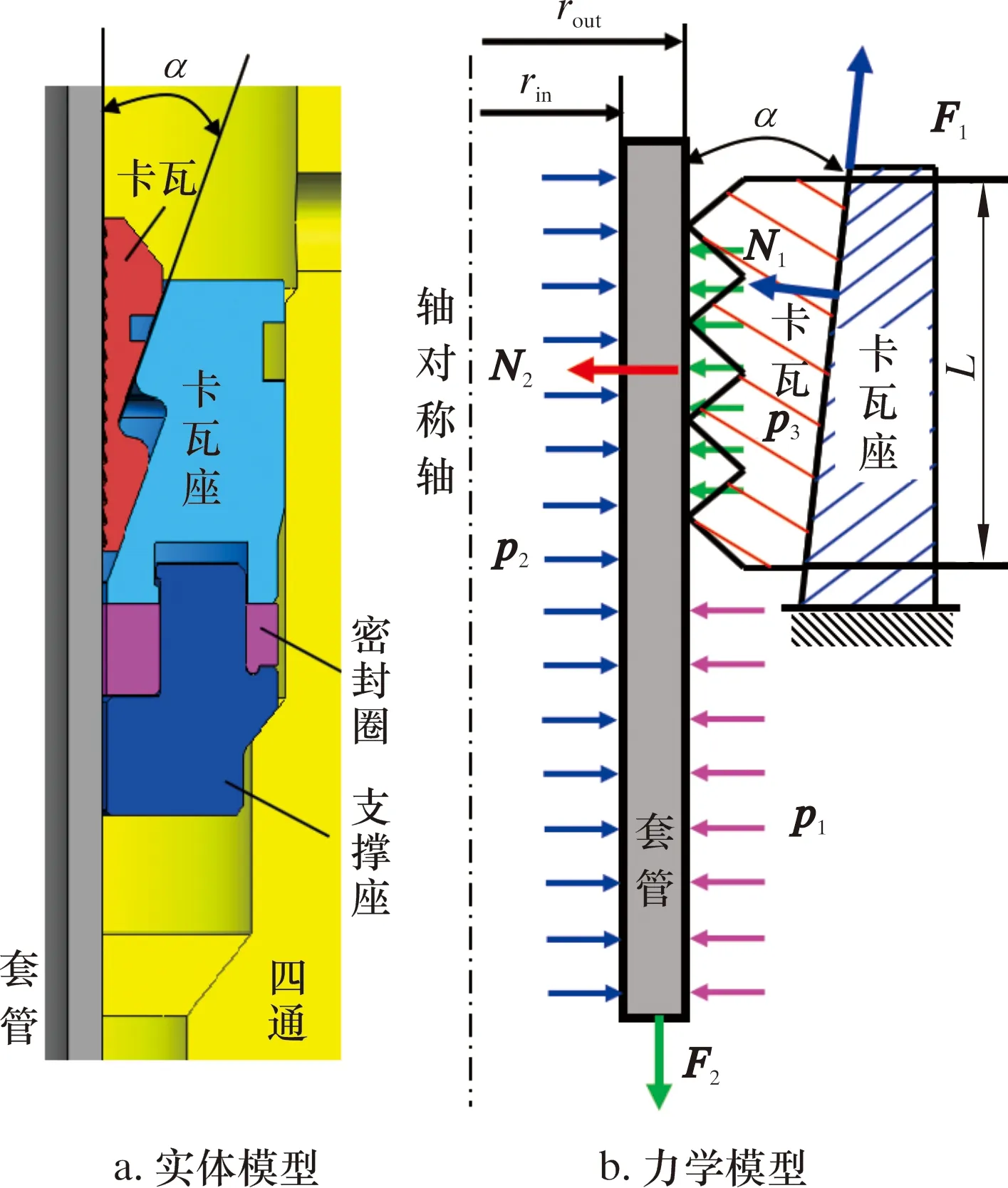
圖3 套管-卡瓦結構軸對稱力學模型Fig.3 Axisymmetric mechanical model of casing-slip structure

卡瓦套管懸掛器簡化力學模型如圖3所示。井口卡瓦懸掛器受到的外載荷主要有：各種作業中套管受到環空壓力p1、井筒內的生產壓力p2、夾持套管的懸重F2，以及F2產生的卡瓦部分外壓力p3。N1為卡瓦與卡瓦座之間總法向力；N2為套管和卡瓦之間總擠壓力；F1為卡瓦與卡瓦座之間總切向力；F2為套管軸向載荷(懸重)；p1為套管外壓，p2為套管內壓；p3為F2引起的卡瓦部分套管外壁平均壓力。

根據材料力學第四強度準則理論[21-23]，當套管內壁的Mises等效應力達到屈服應力σs時，根據圖3b中的力學模型，可推導出卡瓦懸掛套管的拉伸極限載荷，即卡瓦效應拉伸極限載荷Tks，計算模型如下：

(1)

Ts=σsA1

(2)

(3)

AL=2πroutL

(4)

(5)

式中：Ts為無卡瓦效應時的套管軸向拉伸極限載荷，N；μ為摩擦因數；K為橫向載荷系數；AL為卡瓦側向面積，mm2；A1為套管截面面積，mm2；σs為套管屈服強度，MPa；α為卡瓦背面半錐度，(°)；L為卡瓦有效長度，mm；rin、rout分別為套管內、外半徑，mm。

在坐掛過程中，井口套管不存在圖3中的內外壓力p2和p1，只有軸向載荷F2及其引起的橫向載荷N2產生的外擠壓力p3的共同作用。因此由式(1)可以計算出套管的卡瓦效應拉伸極限載荷Tks，該拉伸極限載荷Tks可為下部套管長度或懸重控制提供理論依據。

當套管坐掛和固井后，在各種作業或生產工況下，圖3中將存在內、外壓力p2和p1的作用。該內、外壓力也會影響卡瓦部分套管內的應力分布，這是個復雜的力學過程，用解析解無法計算，只能用有限元法進行仿真模擬計算和評價。

2 卡瓦懸掛器套管受力有限元分析

2.1 套管卡瓦懸掛器基本參數

本文根據新疆某油田超深Xl井，在拆采油四通更換密封件提起采油四通時，發現生產套管管壁上發生橫向斷裂(見圖1)，其使用的?232.5 mm W型卡瓦懸掛器的卡瓦結構有效長度為143 mm，卡瓦背面半錐角為24°，各接觸面之間的摩擦因數為0.25。該X1井套管外徑為232.5 mm，壁厚為16.75 mm，鋼級為155V，線質量約為89.64 kg/m，井深約為7 809 m。由于所有構件均為鋼材，泊松比為0.3，彈性模量為210 GPa，其余強度參數如表1所示。

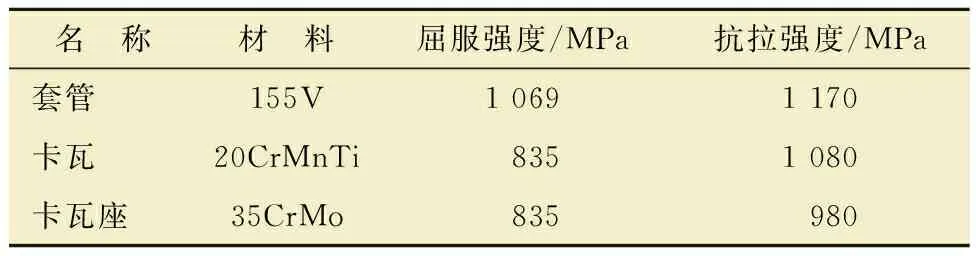
表1 卡瓦懸掛器及套管各材料力學參數Table 1 Mechanical parameters of slip hanger and casing materials

根據以上參數以及式(1)～式(5)，可計算出無卡瓦效應和有卡瓦效應的套管極限載荷，即卡瓦效應的套管拉伸極限載荷，如表2所示。從表2可知，由于存在卡瓦效應，導致套管在卡瓦部分的拉伸極限載荷由12 380 kN降低到了7 010 kN，降低了43.4%。因此理論上在坐掛套管時，下部懸掛載荷必須控制在7 010 kN以內。

表2 坐掛過程中套管的極限載荷變化對比Table 2 Comparison of ultimate load changes of casing during setting process

2.2 有限元模型建立

由于該懸掛器有6瓣結構尺寸相同的卡瓦，且與套管一起呈軸對稱結構，為了減小計算工作量，提高計算速度，根據有限元理論，將該卡瓦懸掛器建立為軸對稱的3D有限元力學模型，如圖4所示。其材料力學參數如表1所示。卡瓦、卡瓦座與套管相互之間為非線性接觸模型，在卡瓦座外壁施加固定約束，卡瓦齒面與套管、卡瓦背面與卡瓦座接觸面分別設置摩擦接觸參數。下部端面施加懸重產生的拉力F2，同時在套管外壁、內壁分別施加壓力p1和p2。為提高計算效率及精確度，在有限元網格劃分時，對卡瓦與套管、卡瓦背面與卡瓦座等接觸部位進行網格加密處理。

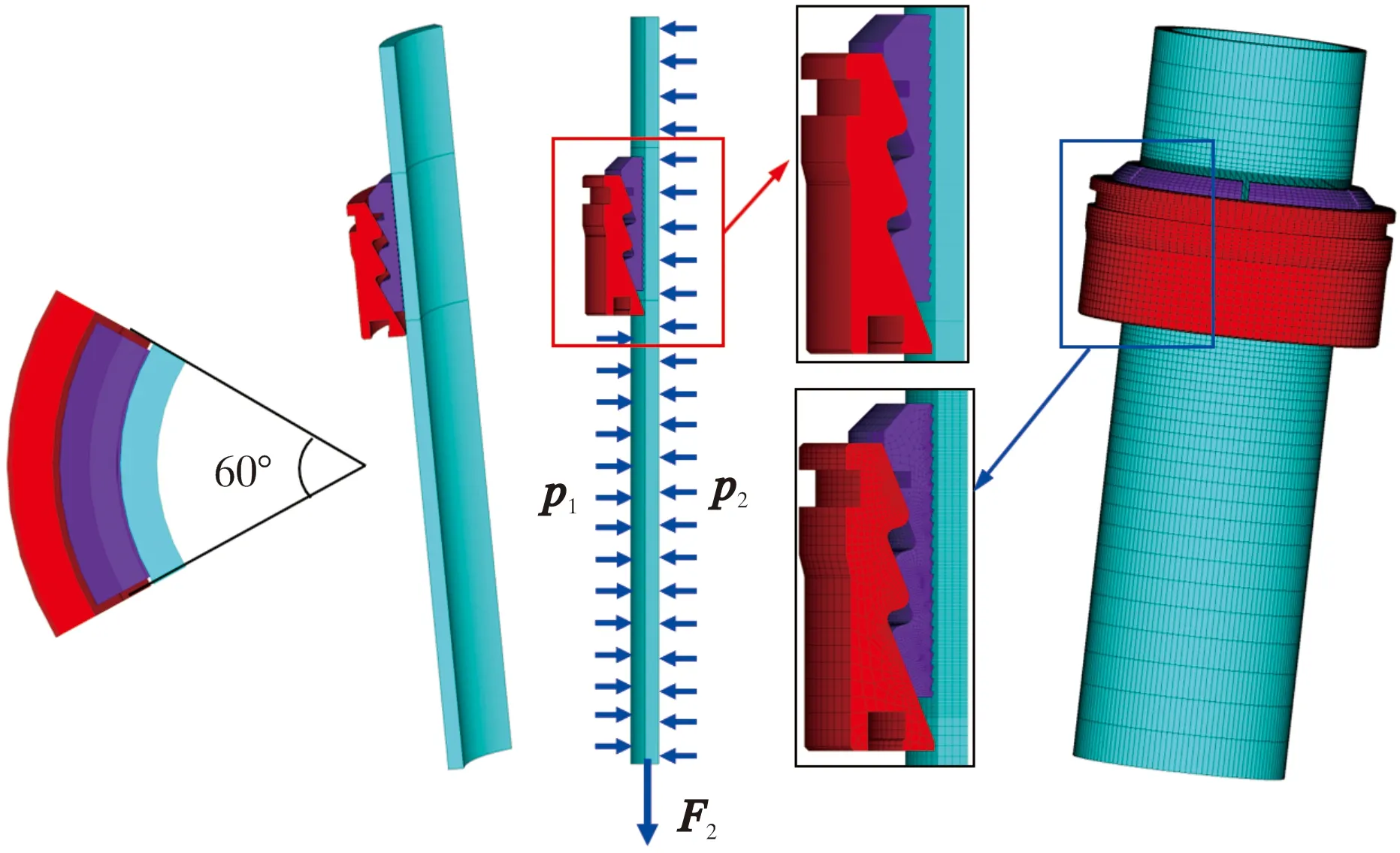
圖4 懸掛器結構有限元力學模型(對稱模型)Fig.4 Finite element mechanical model of hanger structure ( symmetric model)

2.3 坐掛過程套管極限載荷及其下深分析

套管在坐掛過程中，只有軸向載荷F2及其引起的橫向載荷N2產生的外擠壓力p3的共同作用。根據圖4的有限元模型，逐漸增加軸向載荷F2，取出每個計算載荷下卡瓦部分套管外壁的最大Mises應力，通過大量的有限元仿真模擬計算，得到坐掛過程中套管內最大Mises應力隨軸向載荷的變化關系，如圖5所示。

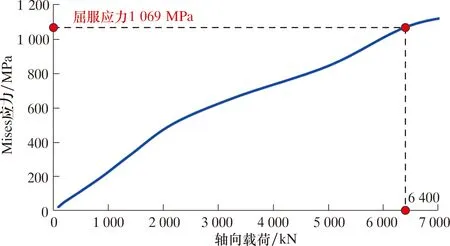
圖5 坐掛過程中套管內最大應力隨軸向載荷的變化關系Fig.5 Variation of maximum stress in casing with axial load during setting process

從圖5可知，套管坐掛過程中，卡瓦部分套管外壁的最大Mises應力隨著軸向載荷的增加呈非線性增加，當軸向載荷達到6 400 kN時，套管上的應力達到其屈服應力1 069 MPa，開始進入塑性變形破壞，即有限元仿真模擬計算出卡瓦效應的套管極限載荷為6 400 kN，小于表2中理論公式計算結果7 010 kN，為理論公式(1)計算結果的0.913倍。這主要是卡瓦效應的應力集中引起的，且有限元仿真模擬計算結果比較接近實際工況，可以通過大量的計算來修正理論公式(1)。本文研究的卡瓦結構套管理論拉伸極限載荷公式(1)的修正系數為0.913。也就是說，如果遇到同樣結構尺寸的卡瓦型號，其套管卡瓦效應的極限載荷可以通過理論公式(1)結果乘以修正系數0.913得到。

圖5中軸向載荷F2=7 000 kN時的有限元計算結果如圖6所示。

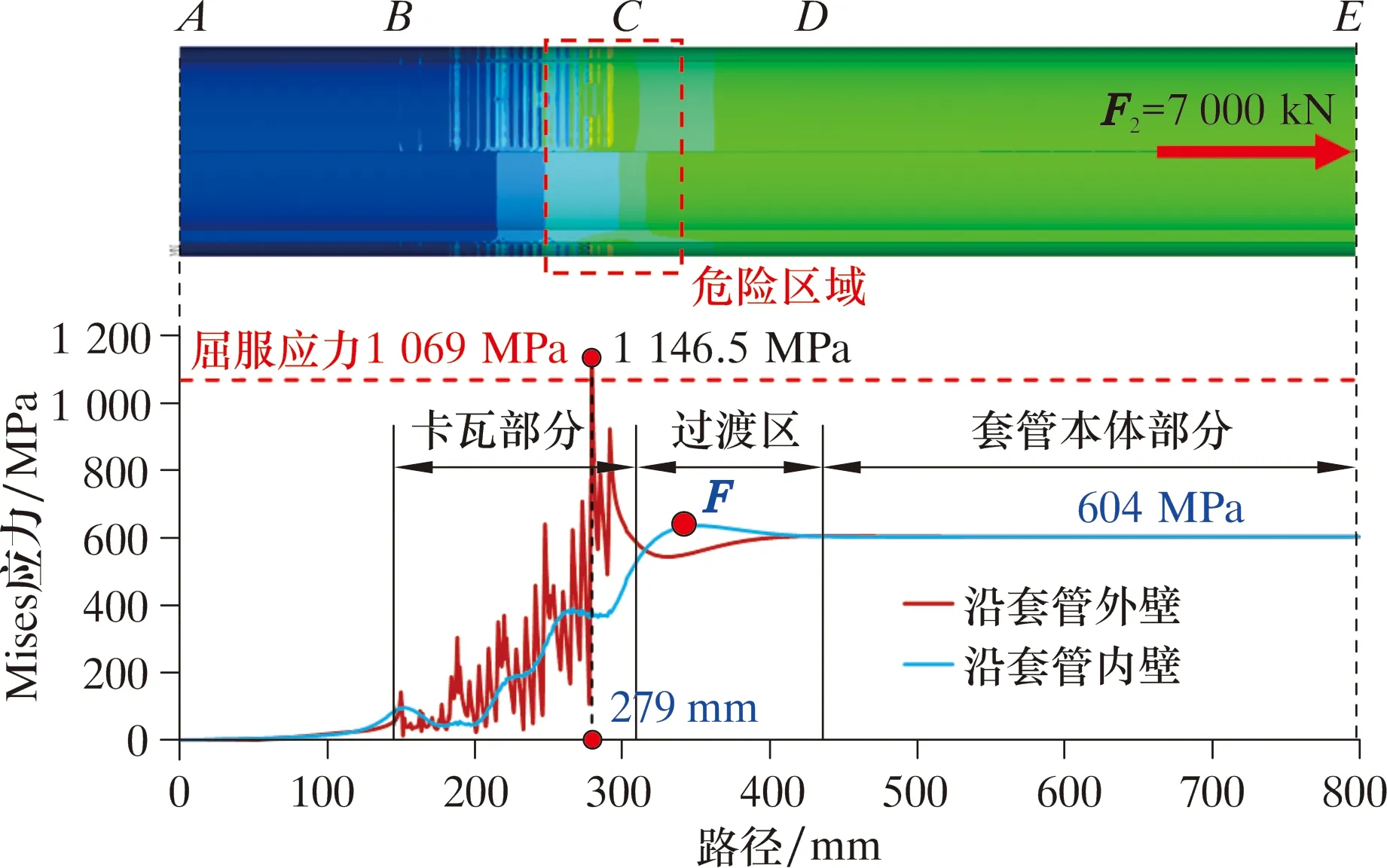
圖6 套管應力云圖及其內、外壁路徑應力變化關系Fig.6 Cloud chart of casing stress and stress variation along inner and outer walls of the casing

由圖6可知，沿套管外壁，在卡瓦部分，距離套管頂部A點位置為279～300 mm的套管出現塑性屈服區域，其最大應力為1 146.5 MPa，超過套管的屈服應力1 069 MPa。該區域是最危險位置，現場套管斷裂位置也發生在此處。在圖6中卡瓦部分，由于卡瓦牙齒引起的應力集中，卡瓦部分套管外壁的應力沿路徑頻繁交變增加，且大部分高于套管內壁應力，但只有外壁應力超過了屈服應力1 069 MPa，所以套管斷裂失效的裂紋首先發生在套管外壁。

從圖6中過渡區路徑曲線可知：套管內、外壁應力發生交變，與卡瓦部分相反，其內壁應力高于外壁應力；遠離過渡區的套管本體部分，其內、外壁路徑上的應力曲線趨于重合，套管本體部分內、外壁應力相等，為604 MPa，這是因為本體只受7 000 kN的拉伸載荷作用，該拉伸載荷除以其橫截面積也剛好等于604 MPa，表明計算工況正確。

卡瓦懸掛器處，套管的軸向載荷F2主要來自于下部套管的懸重。該懸重取決于套管的長度，如果井筒全部掏空，懸重為套管在空氣中的重力；如果井筒內充滿鉆井液或清水，則套管懸重為空氣中的重力減去其在液體中的浮力。根據圖5計算卡瓦效應套管的極限載荷為6 400 kN，考慮套管段重力以及清水密度，可計算出卡瓦懸掛器套管的下深，如表3所示。從表3可知，如果井筒完全掏空，文中研究的X1井套管下到7 809 m大于7 140 m時，處于不安全狀態。但是如果井筒內充滿清水，在浮力作用下，其下深為8 175 m，大于設計井深7 809 m，可滿足安全要求。因此，在下套管時，建議向井筒灌滿清水或鉆井液，以便降低套管懸重，保證其安全坐掛。

表3 卡瓦懸掛器套管安全下深Table 3 Safe setting depth of slip hanger casing

套管坐掛時，套管內、外無壓力，僅受軸向載荷作用，根據表3中的計算結果可得出結論：該卡瓦懸掛器套管的極限載荷為6 400 kN，只要坐掛套管時，其軸向載荷在6 400 kN以內，卡瓦懸掛器套管不會發生塑性變形破壞。

2.4 作業工況套管塑性失效分析

套管在卡瓦懸掛器中坐掛固井后，在實際作業中，套管內、外壁同時受到內、外壓力，但是作用效果會相互抵消，僅受到內壓或外壓作用時為套管受力最惡劣工況。在作業過程中，井筒內壓為0時，只有環空壓力變化的套管塑性變形破壞情況。

根據圖4的有限元模型，軸向載荷從0增加到7 000 kN，作業過程中，套管外壓p1分別為0、50和70 MPa時，通過大量計算，可得套管外壁最大Mises應力隨軸向載荷及其外壓的變化關系，如圖7所示。從圖7可知：套管外壁最大Mises應力隨著軸向載荷及其外壓的增加而增加；當Mises應力達到155V套管的屈服應力1 069 MPa時，套管外壁開始發生塑性變形。根據圖7的計算結果，套管發生塑性破壞的極限載荷如表4所示。從表4可知，作業過程中外壓越高，卡瓦部分套管承受的極限載荷越小，當外壓達到最大設計壓力70 MPa時，極限載荷只有4 500 kN，因此在作業施工時應嚴格控制套管環空壓力。

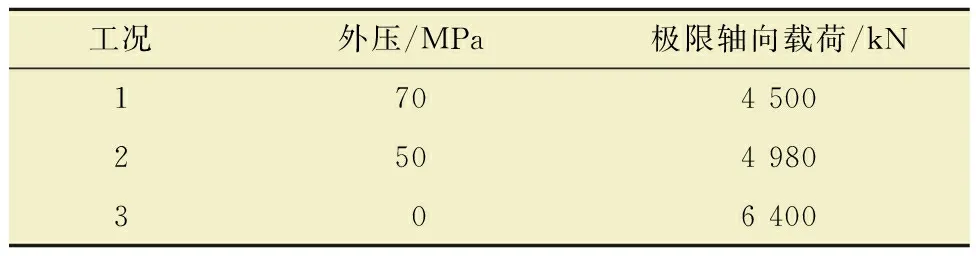
表4 不同作業外壓下卡瓦效應套管的極限載荷Table 4 Ultimate load of slip effect casing at different external pressures

將圖7中環空最大壓力p1=70 MPa時的最后一次計算結果進行應力分布云圖分析，即當坐掛軸向載荷F2=7 000 kN，套管內壓p2=0，按最惡劣工況進行計算，結果如圖8所示。

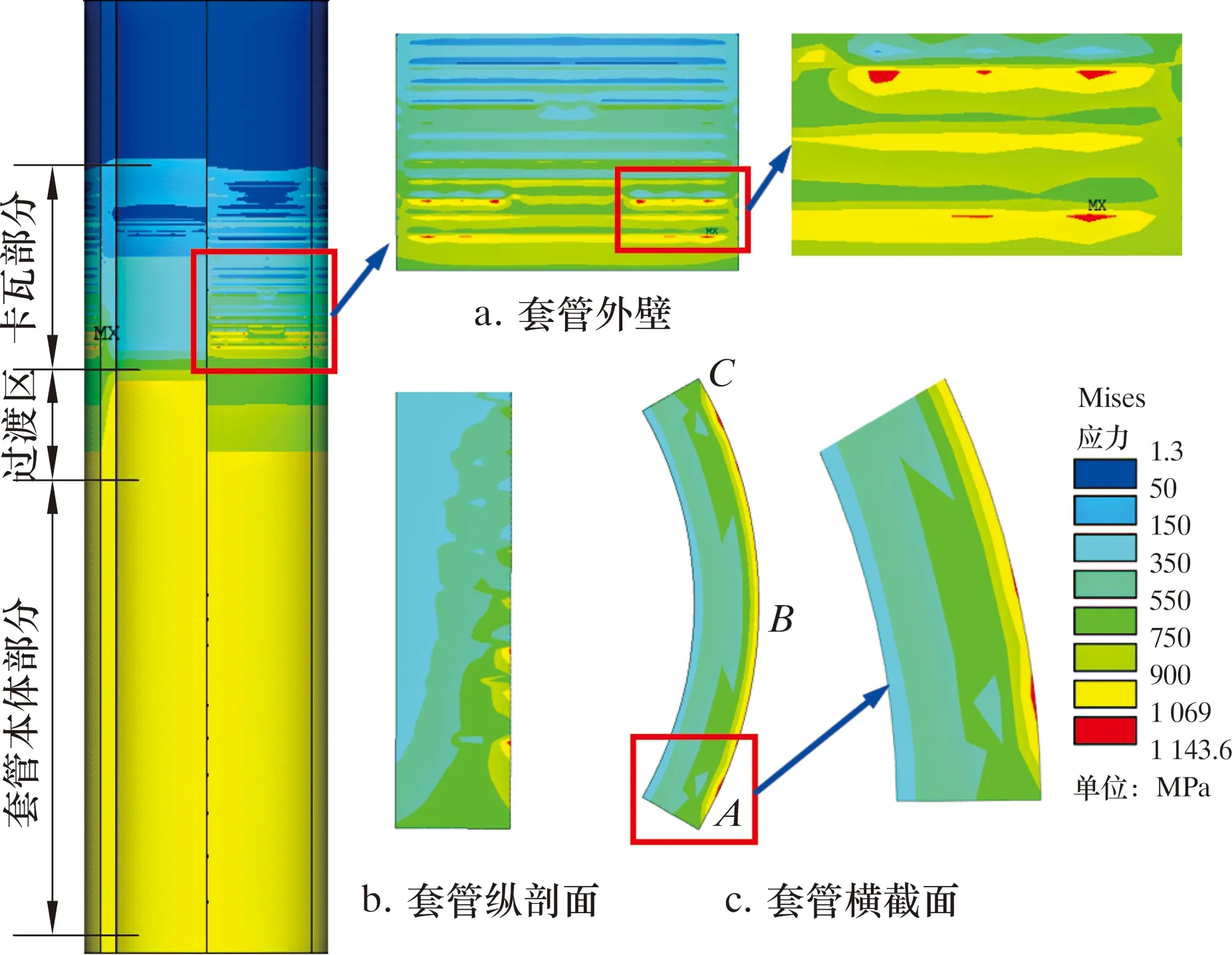
圖8 外壓70 MPa時套管應力分布云圖Fig.8 Cloud chart of casing stress distribution at 70 MPa external pressure

由于受到卡瓦牙的夾持作用，套管外壁出現條狀非均勻分布的應力帶。圖8中Mises應力最大值為1 143.6 MPa，位于卡瓦部分套管的外壁，超過155V套管的屈服應力(1 069 MPa)。圖8a中紅色區為套管塑性破壞區，發生在套管外壁卡瓦牙齒咬入位置，且套管外壁塑性區只有少部分。套管外壁卡瓦牙附近的應力為900.0～1 143.6 MPa，見圖8a～圖8c中的黃色區域，其分布深度見圖8c中ABC位置。此時卡瓦部分套管內壁應力為350～550 MPa，處于彈性變形，即卡瓦部分套管內的應力呈現非均勻分布，尤其是套管外壁非均勻程度較嚴重，其外壁牙痕上存在的應力集中是套管裂紋起裂、斷裂的主要原因。

圖8中過渡區為卡瓦部分套管與下部套管本體的交接部分。從云圖上看，該部分套管內壁應力為黃色區，即應力在900～1 069 MPa之間；外壁應力為綠色區，即應力在550～750 MPa之間過渡區套管同樣處于非均勻應力狀態，只是其非均勻程度比卡瓦部分套管的非均勻程度輕。

從圖8可知，遠離卡瓦的套管本體部分應力呈現均勻分布，受力情況比前2個部分優良。如果套管發生斷裂破壞，首先將發生在卡瓦部分以及過渡區位置，而發生在套管本體上的概率較小。

將圖8中內、外壁沿最大應力路徑數據取出進行分析，結果如圖9所示。由圖9可知，沿套管外壁路徑，在卡瓦部分距離套管頂部A點位置280～300 mm處的套管出現塑性屈服區域，其最大應力為1 143.6 MPa，超過套管的屈服應力1 069 MPa。該區域是最危險位置，現場套管斷裂的位置也發生在此處。過渡區套管內壁F點附近應力達到了屈服應力1 069 MPa，即套管內壁也出現了塑性變形破壞區。而圖6中的工況，此時套管內壁F點應力約為630 MPa，遠低于屈服應力。圖9工況中套管內、外壁均出現了塑性變形區，因此套管在卡瓦部分或過渡區均有可能發生斷裂失效破壞，并且在圖9中遠離過渡區的套管本體部分，其內、外壁路徑上的應力曲線趨于平穩，但是套管本體部分內、外壁應力不相等，分別為977和925 MPa，其差異是外壓70 MPa引起的。

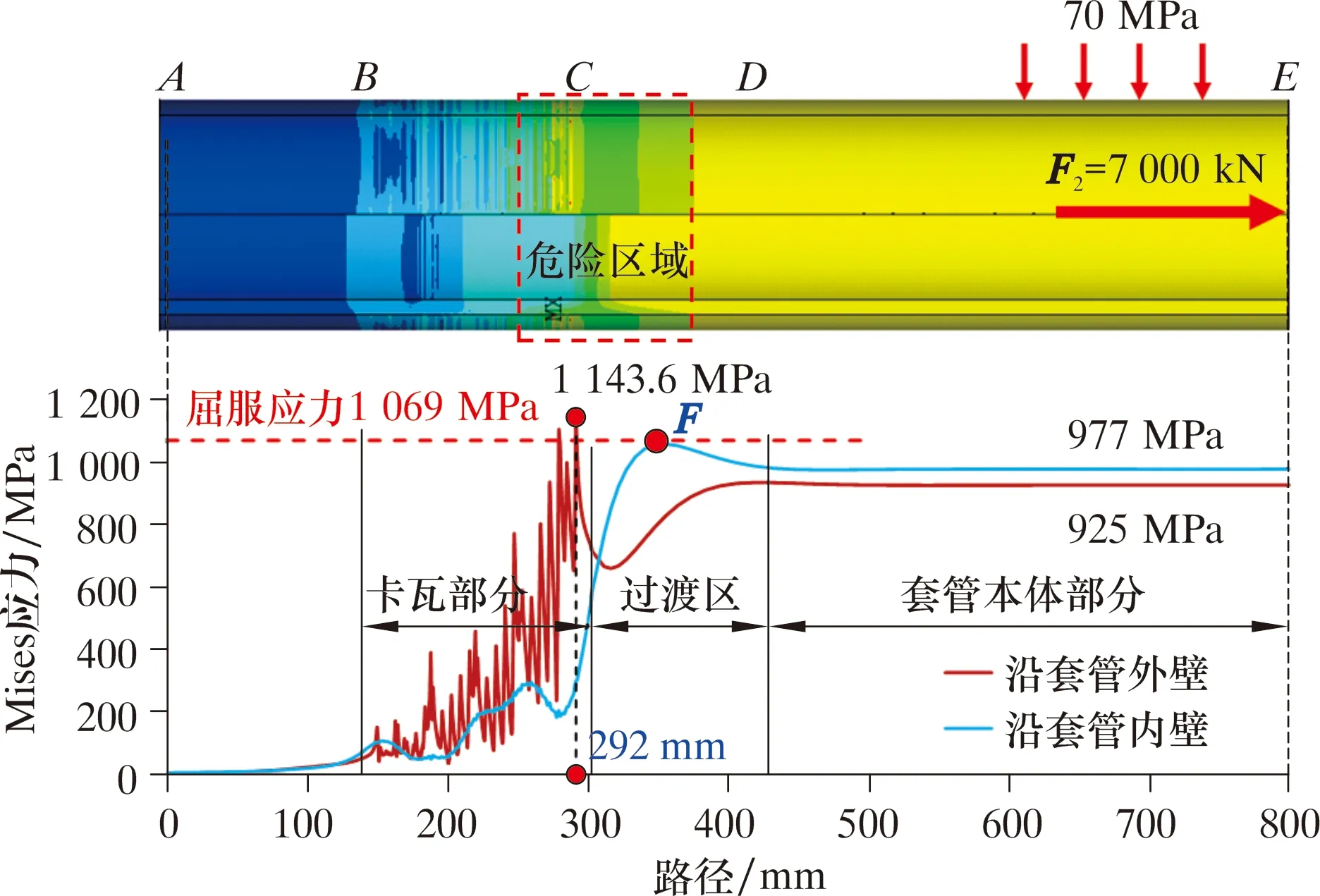
圖9 沿套管內、外壁應力分布曲線Fig.9 Stress distribution curves along inner and outer walls of casing

3 卡瓦應力分析

在圖8工況下，卡瓦上的應力分布如圖10所示。圖10中紅色區為超過卡瓦屈服應力835 MPa的塑性變形區。由于卡瓦牙比較尖銳，吃入套管時產生了較強的應力集中，所以卡瓦牙附近有較寬的塑性硬化區，而卡瓦金屬材料在屈服后存在一定的塑性硬化。由于材料硬化作用，卡瓦的屈服強度將會提高，同時卡瓦牙受套管擠壓，卡瓦背面有卡瓦座支撐，卡瓦始終處于安全狀態，現場數據也證明了這一點。雖然卡瓦處于塑性變形，但是仍能滿足現場使用要求。

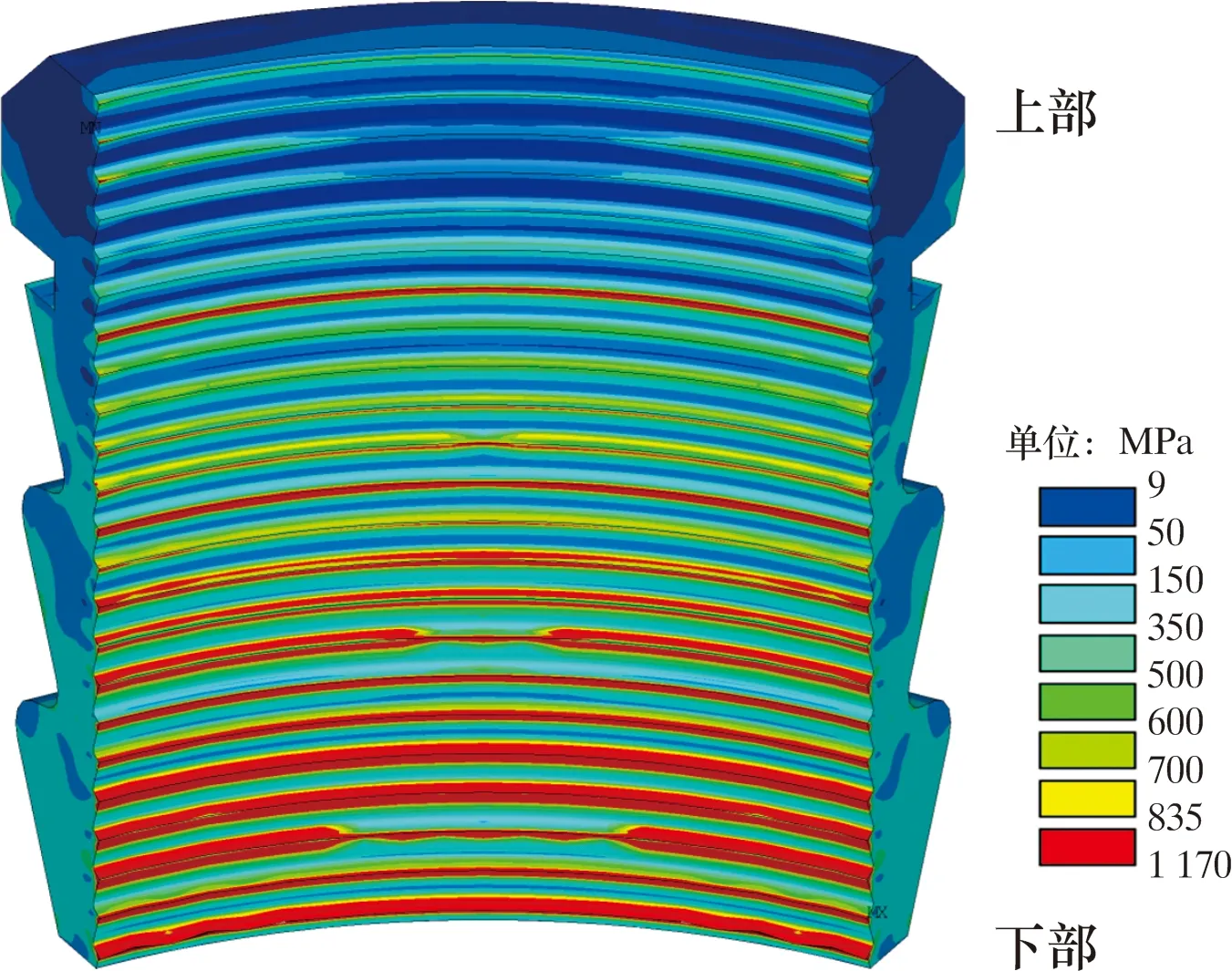
圖10 外壓70 MPa作用下卡瓦應力云圖Fig.10 Cloud chart for stress of slip at 70 MPa external pressure

從卡瓦應力分布云圖可知，卡瓦下部塑性區較多，上部塑性區逐漸減小甚至消失。主要原因是下部卡瓦牙咬入套管后將承擔主要載荷，向上的每一圈應力逐漸遞減，因此卡瓦下部受力較大，從圖8卡瓦部分套管外壁的應力分布也可以得出同樣的應力變化規律。因此，建議選擇無齒痕的卡瓦夾持套管，或者采用全金屬密封的心軸式懸掛器，避免卡瓦懸掛器造成套管損傷破壞。

4 結論及建議

(1)根據?232.5 mm W型卡瓦懸掛器六瓣卡瓦軸對稱結構，建立了卡瓦懸掛器套管坐掛的對稱三維有限元模型。該模型可以仿真模擬套管坐掛以及各種作業工況對套管的塑性損傷破壞，為坐掛極限載荷的評估提供了可靠的理論依據。

(2)根據建立的卡瓦懸掛器有限元模型，得到了卡瓦結構套管理論拉伸極限載荷公式的修正系數為0.913。該修正公式為套管卡瓦效應的極限載荷評價計算提供了簡便的方法和手段。

(3)文中研究的X1井套管實際下深至7 809 m，大于空氣中下深7 140 m，處于不安全狀態。但是如果井筒內充滿清水，在浮力作用下，其下深可達8 175 m，大于設計井深7 809 m，滿足安全要求。因此，在坐掛套管時，建議向井筒灌滿清水或鉆井液，以減小套管懸重，保證安全坐掛。

(4)通過大量的有限元計算，該卡瓦懸掛器套管的極限載荷為6 400 kN，只要坐掛套管時，其軸向載荷控制在6 400 kN以內，卡瓦懸掛器套管不會發生塑性變形破壞。

(5)有限元計算結果表明：卡瓦部分套管內的應力呈現非均勻的應力分布，尤其是套管外壁非均勻程度較嚴重，且外壁存在的牙痕上的應力集中是套管裂紋起裂、斷裂的主要原因；套管在卡瓦部分或過渡區均有可能發生斷裂失效破壞。

(6)由于卡瓦牙夾持處套管外壁應力分布不均，容易產生疲勞裂紋，造成套管外壁損傷，建議選擇無齒痕的卡瓦夾持套管，或者采用全金屬密封的心軸式懸掛器，避免卡瓦懸掛器造成套管損傷破壞。