振動工況下特殊螺紋接頭密封性能仿真研究

于洋 屈展，2 許富艷 曹銀萍 竇益華 劉渝

(1.西北工業大學航空學院 2.西安石油大學石油工程學院 3.上海城建職業學院 4.西安石油大學機械工程學院)

0 引 言

大排量壓裂及高產氣作業過程中，因管內流體壓力及流速的變化引起管柱振動，并在管柱上產生動態載荷[1-2]。特殊螺紋接頭作為油管的連接結構，在復雜的載荷工況下常發生密封失效，甚至由此引發安全事故[3]。傳統的研究多集中于靜力學分析，考慮不同密封結構及載荷工況，分析特殊螺紋接頭等效應力、接觸壓力及接觸長度等對特殊螺紋接頭密封性能的影響[4-6]。許紅林等[7]基于赫茲接觸理論，建立了球面對錐面密封形式的接觸模型，計算了球面半徑對接觸壓力和有效接觸長度的影響。張穎等[8]建立了特殊螺紋接頭泄漏模型，分析了密封面平均接觸壓力、密封面表面粗糙度及密封面有效長度對氣體泄漏率的影響。竇益華等[9-10]基于有限元法，分別考慮不同密封結構、密封面參數及載荷工況，分析了特殊螺紋接頭應力及接觸壓力分布對密封性能的影響。然而，以上基于靜力學分析的方法無法有效解釋因管柱振動引發特殊螺紋接頭密封性能減弱的問題。特殊螺紋接頭密封面可視為2個接觸面，接觸面主要承受法向載荷和切向載荷[11]。外壓力的產生使接觸面法向載荷改變，影響接觸面的接觸形貌及接觸壓力[12-13]；切向載荷由管柱的軸向力產生，可引起密封面的水平滑移[14-15]。振動工況下，特殊螺紋接頭密封面將發生微動，產生能量耗散，導致磨損或疲勞破壞[16]。張穎等[17]建立了密封面的接觸壓力模型，分析了振蕩載荷下不同密封錐度對特殊螺紋接頭能量耗散的影響。李凡等[18-19]將特殊螺紋接頭密封面簡化為剪切層微滑模型，基于能量耗散理論分析了動態載荷下接頭的密封性能。上述研究為特殊螺紋接頭密封性分析提供了新的思路，而建立的模型基于一定的簡化和假設，并未考慮模態振型對密封性能的影響。

為此，本文基于能量耗散理論，考慮振動工況下密封面微觀接觸滑移的影響，建立了錐面-錐面特殊螺紋接頭限元模型，通過振動模態分析，得到含特殊螺紋接頭管柱的模態振型；通過摩擦接觸分析，得到不同模態振型與上扣扭矩下接頭的Von Mises應力、接觸壓力及摩擦力-位移遲滯曲線，據此研究特殊螺紋接頭的密封性能，以期為特殊螺紋接頭上扣扭矩控制及動載作用下密封性能評估提供參考。

1 模態振型的獲取

為了獲取振動工況下特殊螺紋接頭的動態載荷，首先對含有接頭的管柱進行模態分析。以線性模型為基礎，管柱的振動方程為[20-21]：

(1)

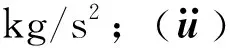
無阻尼力的振動方程為：

(2)

若接頭密封面在模態分析之前已有作用力(如上扣扭矩)，則接觸狀態也會改變，剛度矩陣[K]隨載荷的變化而變化。無阻尼力時式(1)可表示為：

(3)

式(3)中f(t)包含靜態載荷f1(t)與動態載荷f2(t)：

f(t)=f1(t)+f2(t)

(4)

動態載荷的幅值一般小于靜態載荷的幅值，所以該幅值并不能打破由于靜態載荷所建立的結構平衡狀態。施加靜態載荷后系統的剛度矩陣[K1(u)]為：

[K1(u)](u)=f1(t)

(5)

當f1(t)達到終值時，可以得到靜態載荷作用后的終值(u)與[K1(u)]。此時的系統剛度矩陣[K1(u)]可以看作初始剛度矩陣。因此，方程(5)為：

(6)

計算特殊螺紋接頭模態振型與模態頻率分為2部分：第一部分是考慮接觸條件下做一次靜力學非線性分析，第二部分則是用傳統模態分析求得結構的模態振型與模態頻率。

2 特殊螺紋接頭模態分析

基于以上模態分析理論，本文將模態振型的數據以循環位移的方式施加在含有特殊螺紋接頭的油管上，通過提取密封面節點摩擦力與位移，求得各階模態振型下特殊螺紋接頭密封面的能量耗散。以?88.9 mm×6.45 mm錐面-錐面特殊螺紋接頭為研究對象(見圖1)，接頭密封面錐度為1∶2，扭矩臺肩角度為10°，螺紋牙承載面角度為-3°，螺紋牙導向面角度為10°，螺紋錐角為1∶16。

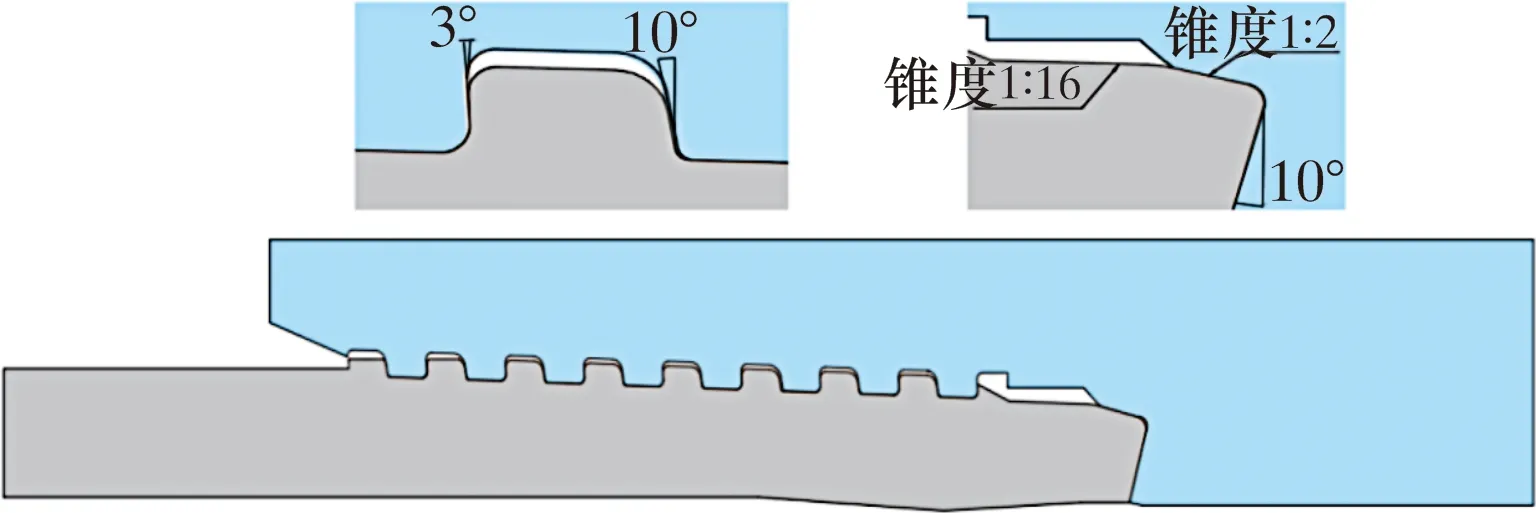
圖1 錐面-錐面特殊螺紋接頭結構示意圖Fig.1 Schematic diagram for structure of cone-cone special threaded connector

建立含有特殊螺紋接頭管柱的有限元模型，如圖2所示，接頭兩端油管長度分別為9.8 m，并將接頭以推薦的上扣扭矩擰緊，油管兩端施加全約束。在上扣扭矩及外載作用下，由于特殊螺紋接頭密封面和螺紋處發生彈、塑性變形，同時接觸面將發生位移，需在ABAQUS軟件中開啟幾何非線性和材料非線性[5]。相關材料參數如下：彈性模量210 GPa，泊松比0.3，摩擦因數0.1，最大屈服強度828 MPa，抗拉強度835 MPa。模型整體選用C3D8I單元，并分別對螺紋、密封面及扭矩臺肩進行網格細化處理。為加快非線性分析的求解速度，同時保證計算的準確性，選用ABAQUS/Standard求解器進行求解分析。

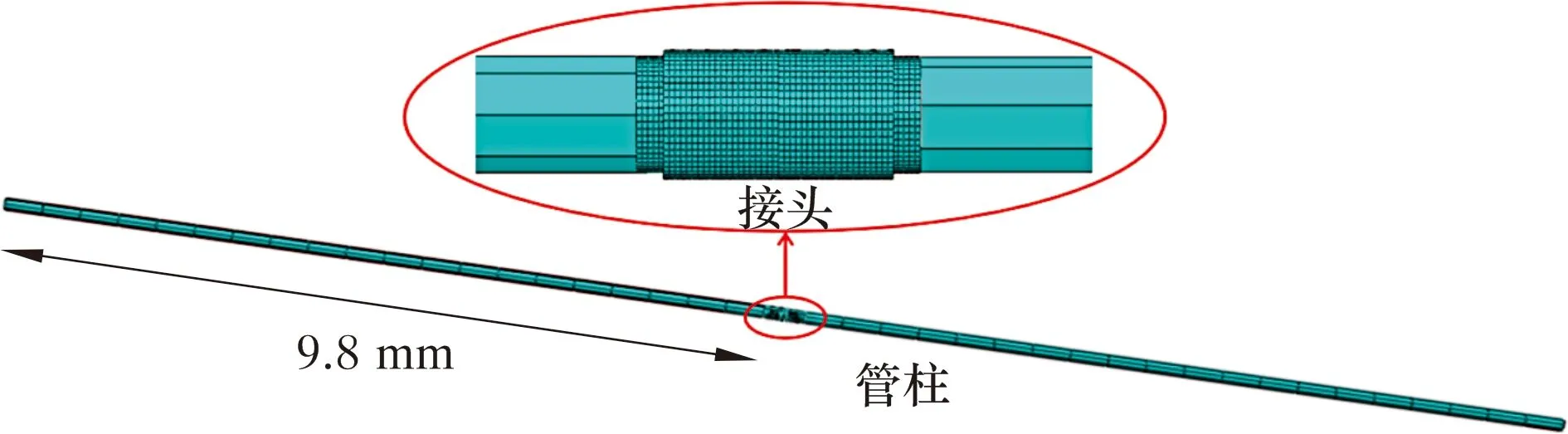
圖2 含有特殊螺紋接頭的管柱有限元模型Fig.2 Finite element model of pipe string with special threaded connector

在分析步程序類型中選擇線性振動[22]，采用頻率的方式創建分析步，計算得到前4階模態振型，如圖3所示。由圖3可知，1階與2階模態振型的最大位移在接頭兩端的油管中部，分別為0.021 4和0.021 7 mm；3階與4階模態振型的最大位移在接頭部位，分別為0.055 41和0.055 45 mm，并發生了整體偏轉。提取模態分析結果中的固有頻率，前4階的固有頻率分別為1.23、1.28、3.58和3.58 Hz。

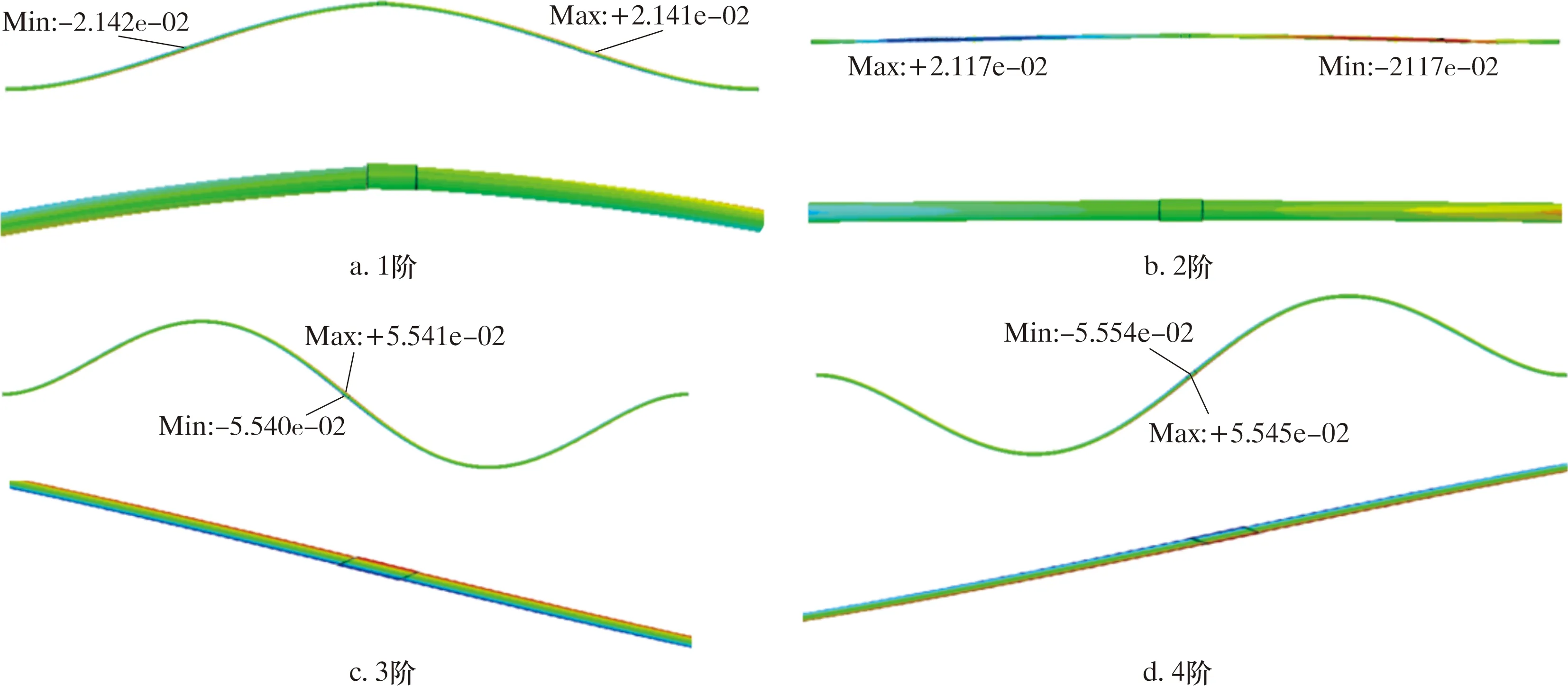
圖3 管柱前4階模態振型Fig.3 First four-order modal shapes of pipe string

3 接頭應力與接觸壓力分析

由于管柱模型1階與2階、3階與4階的軸向位移幅值和固有頻率幾乎相同，故在以下分析中，將1階與3階的位移幅值作為交變位移載荷加載在管柱一端，另一端設置為全約束，然后進行模態振型下的非線性靜力學分析。同時，由于上扣扭矩影響特殊螺紋接頭的接觸狀態及能量耗散，所以考慮了最小、最佳及最大3種上扣扭矩的影響。

3.1 模態振型下特殊螺紋接頭應力分析

不同模態振型與上扣扭矩下特殊螺紋接頭密封面von Mises應力分布云圖如圖4所示。由圖4可知，最大von Mises應力在密封面靠近扭矩臺肩處，但均未超過材料的強度極限835 MPa；交變位移載荷加載完成后，1階與3階模態振型下，密封面最大von Mises應力變化較小，最大差值僅為3 MPa。相應隨時間變化的密封面von Mises應力曲線如圖5所示。

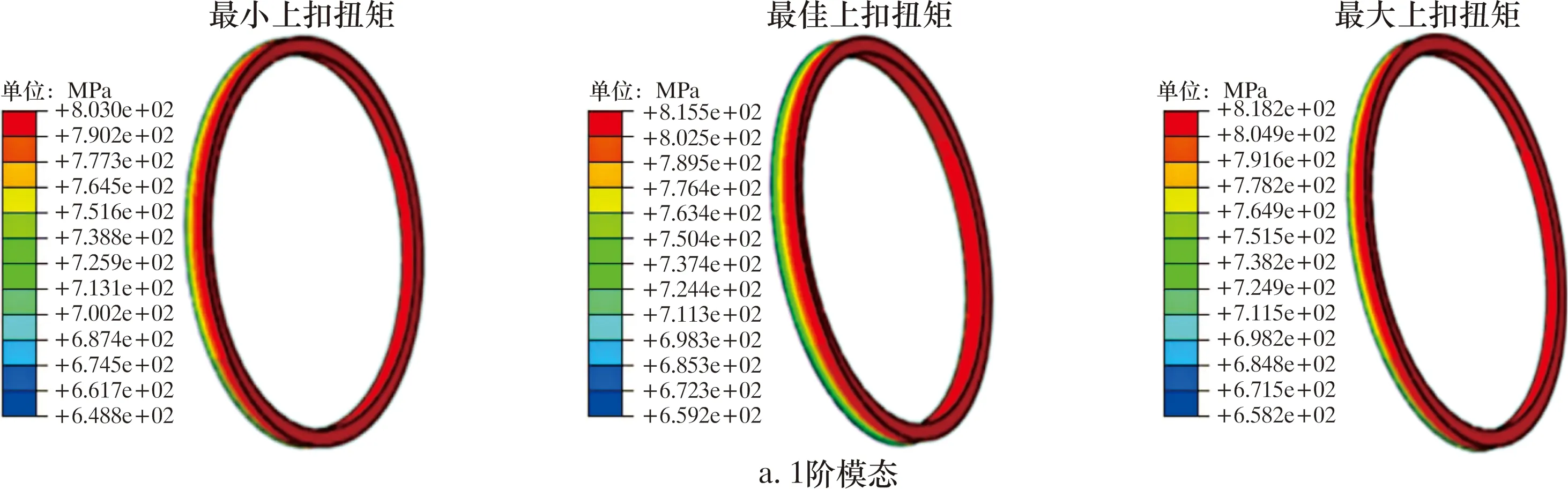
圖4 不同模態振型與上扣扭矩下特殊螺紋接頭密封面von Mises應力云圖Fig.4 Cloud chart for von Mises stress of sealing surface of special threaded connector under different modal shapes and make-up torques

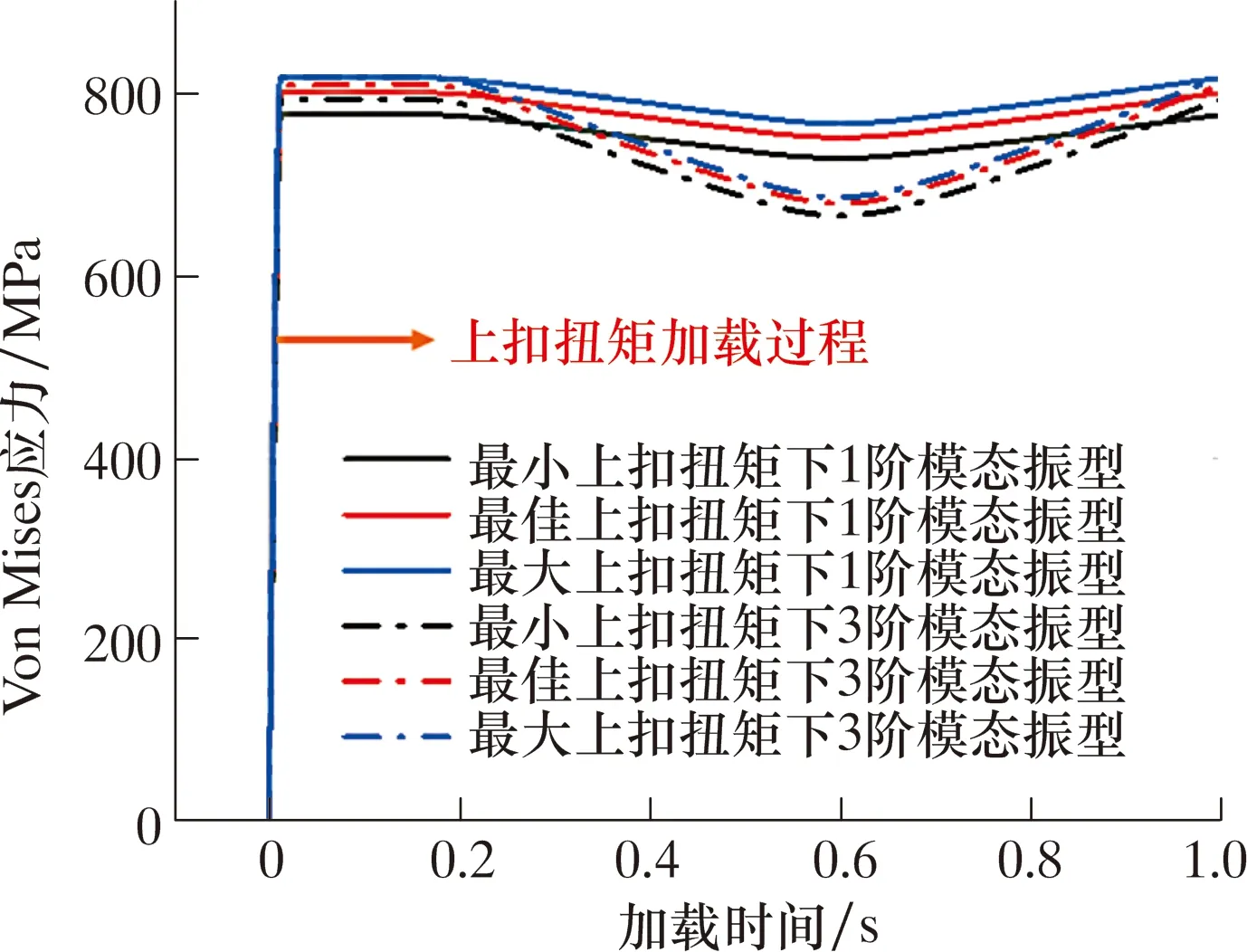
圖5 不同模態振型與上扣扭矩下特殊螺紋接頭密封面von Mises應力曲線Fig.5 Von Mises stress curve of sealing surface of special threaded connector under different modal shapes and make-up torques

圖5中，0 s為上扣扭矩加載過程，0～0.4 s為軸向壓縮位移加載與卸載過程，0.4～0.8 s為軸向拉伸位移加載與卸載過程。2種模態振型加載與卸載過程中，von Mises應力呈V形變化，沒有應力顯著增大的現象。僅在3階模態振型下，當軸向拉伸位移達到峰值時，密封面von Mises應力最小。這是因為3階模態振型的位移較大(約為1階的2.6倍)，使得密封面向油管端的滑移量增加，密封面的過盈量減小，從而導致von Mises應力減小。以上分析表明，1階振型與3階振型對特殊螺紋接頭的應力影響較小。

3.2 模態振型下特殊螺紋接頭接觸壓力分析

不同模態振型與上扣扭矩下特殊螺紋接頭密封面接觸壓力分布如圖6所示。由圖6可知，交變位移載荷加載完成后，2種模態振型下最大接觸壓力同樣位于密封面靠近扭矩臺肩處，且密封面均保持了較高的接觸壓力。相應隨時間變化的密封面接觸壓力曲線如圖7所示。

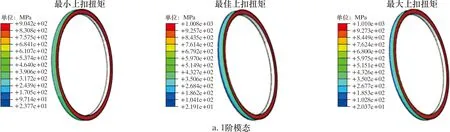
圖6 不同模態振型與上扣扭矩下特殊螺紋接頭密封面接觸壓力云圖Fig.6 Cloud chart for contact pressure of sealing surface of special threaded connector under different modal shapes and make-up torques

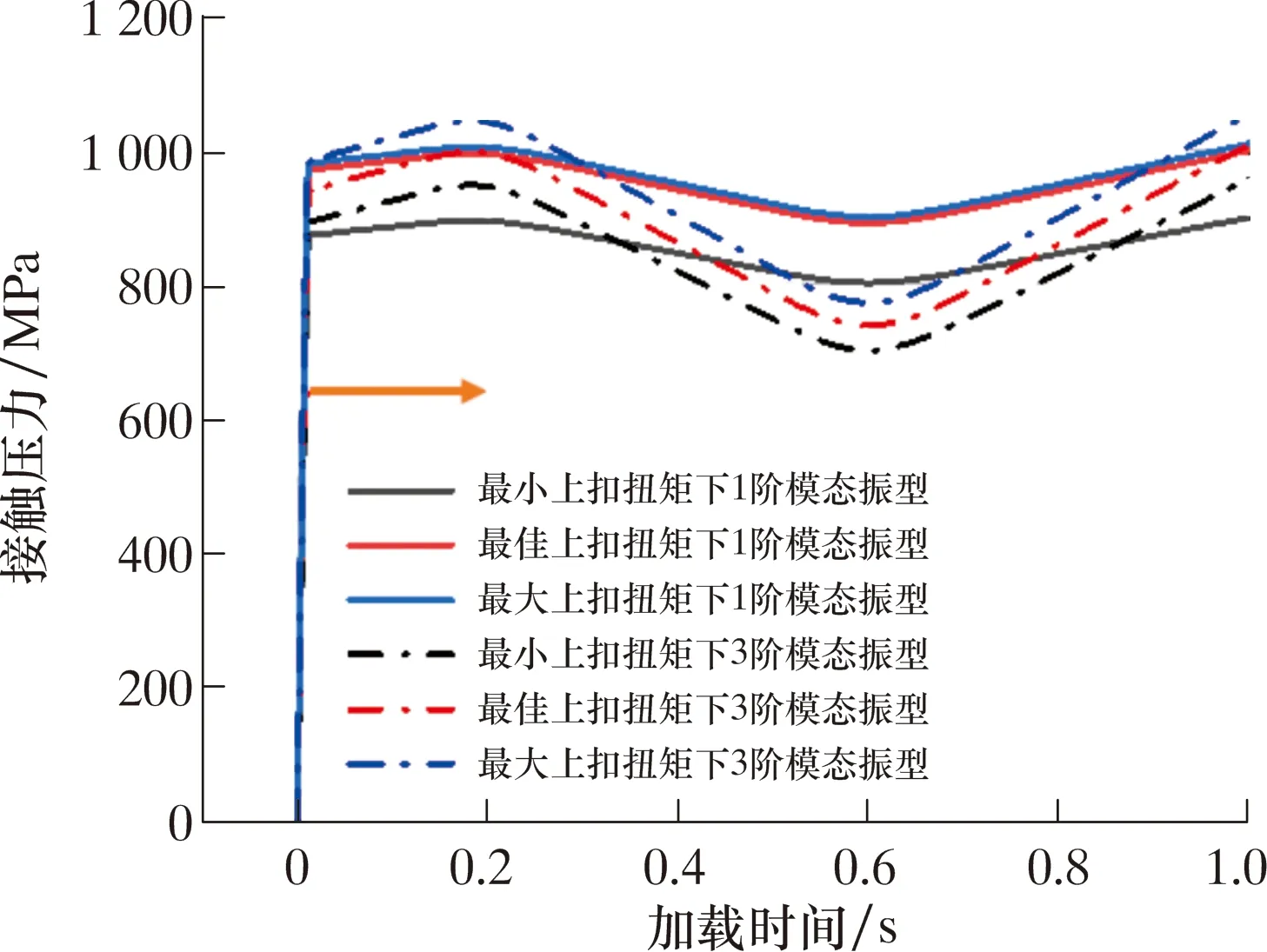
圖7 不同模態振型與上扣扭矩下特殊螺紋接頭密封面接觸壓力曲線Fig.7 Contact pressure curve of sealing surface of special threaded connector under different modal shapes and make-up torques

由圖7可以看出，1階與3階模態振型下，3種上扣扭矩的密封面接觸壓力隨時間均呈正弦曲線規律變化，且3階模態振型的變化幅值較大。雖然3階模態振型下在加載軸向拉伸位移時，最小上扣扭矩的密封面接觸壓力的降幅最大，但仍保持了較高的接觸壓力(值為673 MPa)。在1個周期的交變位移載荷加載結束后，密封面的接觸壓力與初始值基本持平。

由以上分析可知，模態振型對特殊螺紋接頭密封面von Mises應力及接觸壓力的影響并不明顯，利用兩者分析振動工況下接頭密封性能具有一定的局限性。

4 接頭能量耗散與密封性能分析

在外部遞增載荷作用下，密封面首先發生微觀滑移(黏著與滑移共存)。隨著載荷進一步增大，密封面發生宏觀滑移。在1個循環載荷作用周期內，各種滑移相互轉換，出現力-位移遲滯現象，則力與位移遲滯曲線包含的面積即為1個周期內密封面產生的能量耗散[16]。

不同模態振型與上扣扭矩下密封面摩擦力、位移隨時間變化曲線如圖8所示。由圖8可知：1階模態振型下力、位移曲線重合度較高；3階模態振型下密封面的力、位移分離度較大，表明后者的遲滯現象較明顯。提取圖8中密封面位移、摩擦力的幅值，如表1所示。

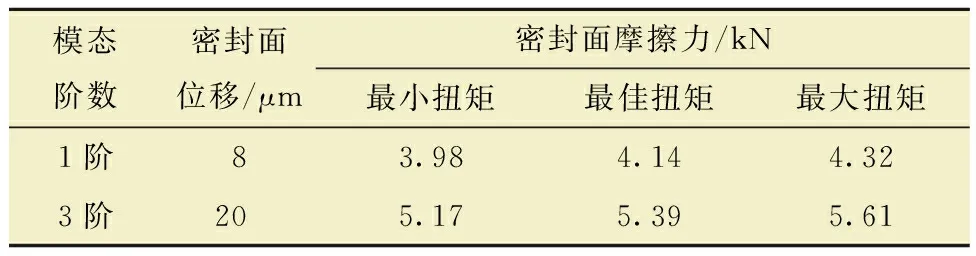
表1 不同模態振型與上扣扭矩下密封面摩擦力與位移幅值Table 1 Friction and displacement amplitude of sealing surface under different modal shapes and make-up torques

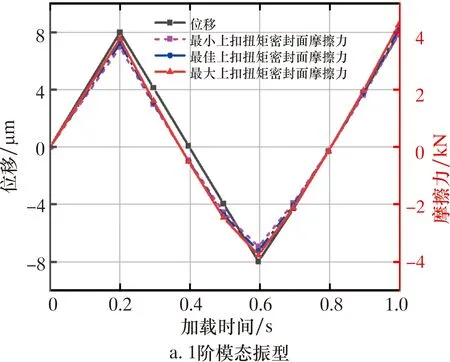
圖8 不同模態振型與上扣扭矩下密封面摩擦力與位移隨時間變化曲線Fig.8 Time dependent curves of friction and displacement of sealing surface under different modal shapes and make-up torques

由表1可以看出，模態振型下，特殊螺紋接頭密封面的位移為微米級，且摩擦力隨上扣扭矩的增大而增大。3階模態振型下，密封面的滑移量和摩擦力的變化幅值分別為1階模態振型的2.5和1.3倍。

不同模態振型與上扣扭矩下密封面摩擦力-位移遲滯曲線如圖9所示。

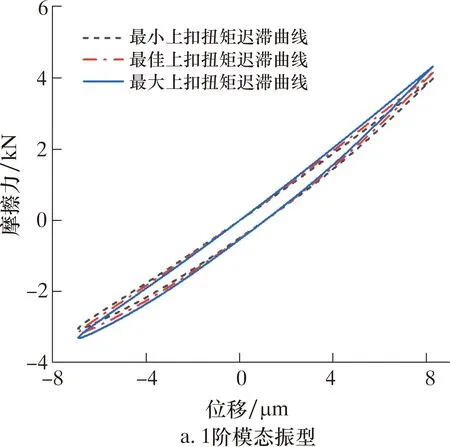
圖9 不同模態振型與上扣扭矩下密封面摩擦力-位移遲滯曲線Fig.9 Friction-displacement lag curves of sealing surface under different modal shapes and make-up torques

由圖9可知，2種模態振型下，密封面的遲滯曲線均呈“針葉”形，處于微觀滑移狀態，沒有宏觀滑移。由Mindlin理論可知，此時密封面的接觸邊緣發生微觀滑移，而中心處于黏著狀態[16]。相較于1階模型振型，3階模態振型下密封面黏著區域較小，微觀滑移較大。通過計算遲滯曲線的面積，得到相應的能量耗散，如圖10所示。由圖10可知：3階模態振型下密封面的能量耗散約為1階模態的3.2倍；相同模態振型下，上扣扭矩越大，能量耗散越大。振動工況產生的能量耗散可以造成接觸面摩擦磨損，也可加速疲勞裂紋的萌生[23]，導致特殊螺紋接頭密封性能減弱。在長期振動作用下，將導致接頭密封失效或使用壽命縮短。因此，利用力-位移遲滯曲線分析密封面的接觸滑移狀態及能量耗散，可以明顯反映出振動工況對特殊螺紋接頭密封性能的影響。

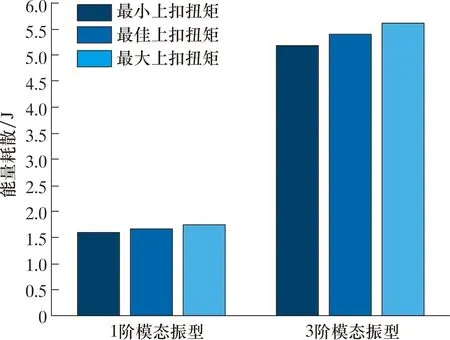
圖10 不同模態振型與上扣扭矩下密封面能量耗散Fig.10 Energy dissipation of sealing surface under different modal shapes and make-up torques

以上研究表明，振動工況下特殊螺紋接頭密封面的滑移量極小，可達到微米級，這對基于靜力學分析接頭von Mises應力及接觸壓力的影響并不明顯，不能有效解釋因振動引發特殊螺紋接頭密封性能減弱的問題。而利用能量耗散理論從微觀層面研究接頭密封性能的方法，可以有效解決這一問題。

5 結 論

(1)模態振型對特殊螺紋接頭密封面von Mises應力及接觸壓力的影響并不明顯，而基于能量耗散理論，利用力-位移遲滯特性分析密封面的接觸滑移狀態及能量耗散，可從微觀層面解釋因管柱振動引發特殊螺紋接頭密封性能減弱的問題。

(2)模態振型下，特殊螺紋接頭密封面間的摩擦力與能量耗散均隨上扣扭矩的增大而增大；3階模態振型下，密封面的摩擦力、位移遲滯現象明顯，其能量耗散值大于1階模態。

(3)模態振型下，特殊螺紋接頭密封面的位移為微米級，密封面的摩擦力-位移遲滯曲線呈“針葉”形，處于黏著與滑移共存的微觀滑移狀態。長期振動工況下，易造成密封面磨損，導致特殊螺紋接頭密封性能減弱甚至密封失效。