正方形自填充蜂窩結(jié)構(gòu)異面平臺(tái)應(yīng)力的研究

孫德強(qiáng)，葛鳳，張超，崔燕燕，本金翠，常露，高璐璐，王倩

正方形自填充蜂窩結(jié)構(gòu)異面平臺(tái)應(yīng)力的研究

孫德強(qiáng)1，葛鳳1，張超2，崔燕燕1，本金翠1，常露1，高璐璐1，王倩1

（1.陜西科技大學(xué) a.中國(guó)輕工業(yè)功能印刷與運(yùn)輸包裝重點(diǎn)實(shí)驗(yàn)室 b.輕化工程國(guó)家級(jí)實(shí)驗(yàn)教學(xué)示范中心 c.3S包裝新科技研究所，西安 710021；2.西安西電變壓器有限責(zé)任公司，西安 710077）

為了促進(jìn)正方形自填充蜂窩的合理使用，研究其異面平臺(tái)應(yīng)力隨沖擊速度、壁厚邊長(zhǎng)比和自填充級(jí)數(shù)的變化規(guī)律。利用ANSYS/LS-DYNA建立基于胞元陣列的正方形自填充蜂窩異面沖擊分析的有限元模型。對(duì)自填充級(jí)數(shù)為0的正方形蜂窩進(jìn)行異面壓縮試驗(yàn)和相應(yīng)的仿真分析，證明有限元模型的可靠性。基于簡(jiǎn)化的超折疊單元理論，建立蜂窩準(zhǔn)靜態(tài)平臺(tái)應(yīng)力的理論模型，并證明理論模型的可靠性。正方形自填充蜂窩在大的壁厚邊長(zhǎng)比和沖擊速度下?lián)碛懈叩膭?dòng)態(tài)平臺(tái)應(yīng)力；在自填充級(jí)數(shù)由0變?yōu)?時(shí)，動(dòng)態(tài)平臺(tái)應(yīng)力增長(zhǎng)率最大。在其他因素不變的情況下，正方形自填充蜂窩的異面動(dòng)態(tài)平臺(tái)應(yīng)力與沖擊速度的平方呈線性關(guān)系，與壁厚邊長(zhǎng)比呈冪指函數(shù)關(guān)系，其增長(zhǎng)率隨自填充級(jí)數(shù)逐級(jí)遞減。基于數(shù)值模擬結(jié)果，得到了不同自填充級(jí)數(shù)下正方形自填充蜂窩異面動(dòng)態(tài)平臺(tái)應(yīng)力的經(jīng)驗(yàn)公式。

正方形自填充蜂窩；異面沖擊；有限元模擬；平臺(tái)應(yīng)力

蜂窩常作為蜂窩板夾芯材料，具有質(zhì)量小、比強(qiáng)度高、比剛度大、穩(wěn)定性好和吸能特性良好等諸多優(yōu)異性能，在包裝、汽車、船舶和建筑等領(lǐng)域內(nèi)有著廣泛的應(yīng)用[1-3]。目前，較為常見(jiàn)的蜂窩芯材結(jié)構(gòu)有六邊形[4]、方形[5]、三角形[6]等構(gòu)型，有關(guān)其靜動(dòng)態(tài)力學(xué)性能已經(jīng)開(kāi)展了大量的研究。

隨著蜂窩應(yīng)用和工程需求的日益擴(kuò)大，促使蜂窩向更輕和更強(qiáng)的方向發(fā)展，因此新的蜂窩不斷被提出，其中對(duì)蜂窩進(jìn)行填充是一種有效提高整體吸能特性的新思路。Liu等[7]通過(guò)對(duì)EPP泡沫填充和未填充蜂窩板進(jìn)行共異面壓縮試驗(yàn)，發(fā)現(xiàn)隨著EPP填料的增加，蜂窩的平均平臺(tái)應(yīng)力和總能量吸收顯著提高。彭琦[8]通過(guò)對(duì)一種聚氨酯泡沫填充類蜂窩進(jìn)行共異面的數(shù)值模擬，發(fā)現(xiàn)泡沫填充后顯著提高了類蜂窩的共異面耐撞性能。此外，蜂窩還有其他的填充方式，如Zhang等[9]將圓柱形管填充到正方形、六邊形和八邊形蜂窩的不同位置，構(gòu)成了一種仿生多胞蜂窩，對(duì)其進(jìn)行了理論與仿真分析，得到一種具有優(yōu)異吸能效果的結(jié)構(gòu)。Wu等[10]在正方形管中加入加強(qiáng)筋，使其成為多單元薄壁結(jié)構(gòu)，對(duì)其進(jìn)行試驗(yàn)和有限元分析，發(fā)現(xiàn)隨著多胞管數(shù)量的增加，其平均平臺(tái)應(yīng)力和比能量吸收得到明顯提高。Zhang等[11]在六邊形蜂窩的基礎(chǔ)上，用較小的規(guī)則六邊形迭代構(gòu)造了一種六邊形分層蜂窩，通過(guò)對(duì)0、1和2階3種分層蜂窩進(jìn)行仿真分析得到，在相對(duì)密度一定的情況下，其總能量吸收隨著階數(shù)的增加而增大。

受到上述填充方式的啟發(fā)，本文以正方形蜂窩為例，構(gòu)建一種同種構(gòu)型蜂窩進(jìn)行“自填充”的蜂窩結(jié)構(gòu)，即正方形自填充蜂窩（Square Self-filled Honeycomb，簡(jiǎn)稱SSF蜂窩）。建立可靠的用于沖擊分析的有限元模型，推導(dǎo)其異面靜態(tài)平臺(tái)應(yīng)力理論公式，并基于大量參數(shù)化仿真計(jì)算來(lái)探究沖擊速度、壁厚邊長(zhǎng)比和自填充級(jí)數(shù)對(duì)其異面平臺(tái)應(yīng)力的影響規(guī)律，以此為SSF蜂窩優(yōu)化設(shè)計(jì)提供理論支撐。

1 數(shù)值模擬分析

1.1 正方形自填充蜂窩

如圖1所示，SSF蜂窩是由不同的正方形以內(nèi)接方式逐級(jí)填充的。圖1中的、1、2代表著逐級(jí)正方形的邊長(zhǎng)，滿足式（1）所示關(guān)系，其中為自填充級(jí)數(shù)。假設(shè)所有蜂窩胞元的壁厚為，異面方向上蜂窩的高度為。

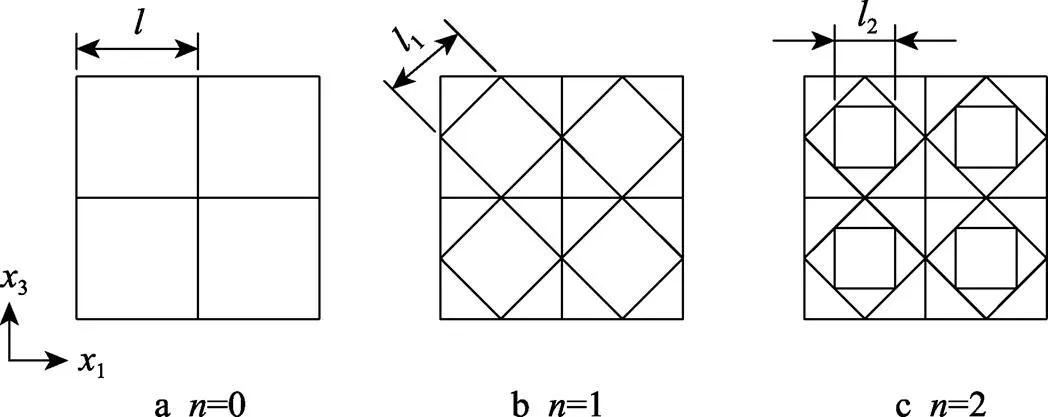
圖1 正方形自填充蜂窩結(jié)構(gòu)示意圖

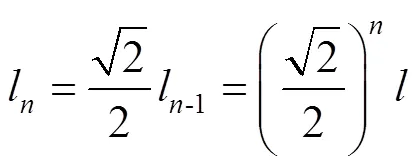
1.2 有限元模型

本文借助ANSYS/LS-DYNA建立SSF蜂窩異面動(dòng)態(tài)沖擊分析的有限元模型，如圖2所示。蜂窩體夾在2個(gè)剛性壓板之間，支撐板2固定，壓縮板1以恒定速度向下勻速壓縮試樣。蜂窩胞壁使用5個(gè)積分點(diǎn)的Belystchko-Tsay殼單元shell 163進(jìn)行網(wǎng)格劃分，單元邊長(zhǎng)為0.5 mm。沿用Sun等[12]所用材料參數(shù)模型，蜂窩樣品之間定義為Self-contact接觸，蜂窩體與兩剛性壓板間定義Auto Surface-to-surface接觸，靜動(dòng)摩擦因數(shù)均為0.2。

圖2 正方形自填充蜂窩在異面沖擊下的有限元模型

1.3 有限元模型可靠性驗(yàn)證

1.3.1 樣品壓縮試驗(yàn)

為了驗(yàn)證文中有限元仿真建模方法的可靠性，對(duì)2×2的正方形蜂窩胞元陣列進(jìn)行靜態(tài)壓縮試驗(yàn)，試驗(yàn)樣品如圖3a所示。其基材為6063 T5型鋁合金，胞元長(zhǎng)=20 mm、高度=50 mm、壁厚=0.8 mm。利用萬(wàn)能材料試驗(yàn)機(jī)對(duì)試樣進(jìn)行靜態(tài)壓縮，壓縮速度為10 mm/min；上壓板的最大位移為40 mm。

圖3 壓縮試驗(yàn)樣品與設(shè)備

1.3.2 基材拉伸試驗(yàn)

參照GB/T 16865—2013[13]制作6063 T5型鋁合金的拉伸試樣，加工尺寸如圖4所示。單軸拉伸試驗(yàn)也在萬(wàn)能材料試驗(yàn)機(jī)上進(jìn)行，拉伸速率為2 mm/min。從圖5所示的拉伸應(yīng)力-應(yīng)變曲線中計(jì)算得到基材的材料參數(shù)：彈性模量s=68 GPa、屈服應(yīng)力s=180 MPa、正切模量t=682 MPa、泊松比=0.33、密度s=2 700 kg/m3。

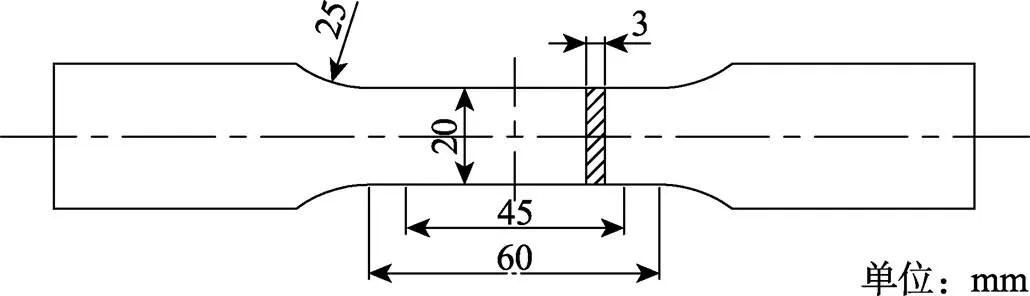
圖4 試樣加工尺寸

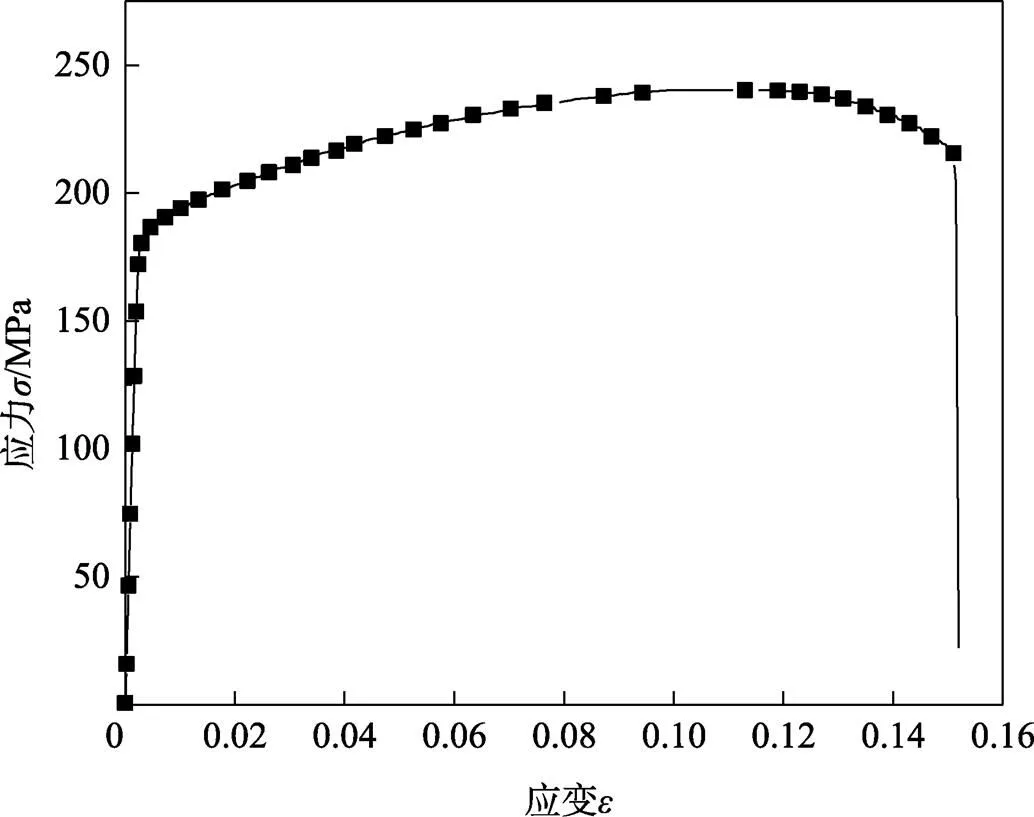
圖5 基材試樣拉伸試驗(yàn)的σ-e曲線

1.3.3 試驗(yàn)和仿真結(jié)果分析

假設(shè)壓縮應(yīng)變?yōu)椋瑘D6是試驗(yàn)和仿真得到的變形模式。從圖6中可以看出，蜂窩試樣首先在靠近支撐端位置產(chǎn)生褶皺變形，隨后向上漸進(jìn)折疊壓縮直至密實(shí)，這與有限元仿真變形模式相一致。圖7是試驗(yàn)和有限元仿真得到的應(yīng)力-應(yīng)變曲線和平臺(tái)應(yīng)力，發(fā)現(xiàn)兩者的應(yīng)力-應(yīng)變曲線具有很好的一致性，平臺(tái)應(yīng)力的誤差在3.18 %左右。由此證明該有限元模型是可靠的，可以用于后續(xù)的仿真分析。

圖6 試驗(yàn)與仿真的變形模式對(duì)比

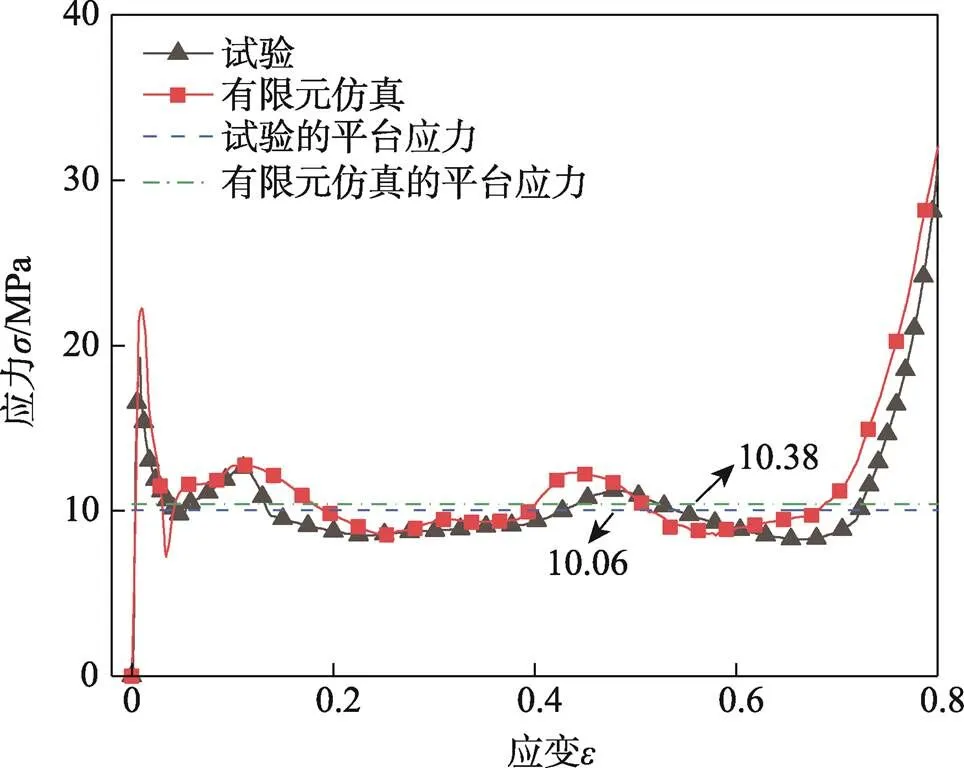
圖7 正方形蜂窩樣品的σ-e曲線和平臺(tái)應(yīng)力

2 理論分析

2.1 異面靜態(tài)平臺(tái)應(yīng)力理論模型

Chen等[14]提出的簡(jiǎn)化的超折疊單元理論認(rèn)為，薄壁結(jié)構(gòu)在異面壓縮變形的過(guò)程中，變形能由塑性鉸鏈形成的彎曲能量B和膜拉伸的應(yīng)變能m兩部分組成，即：

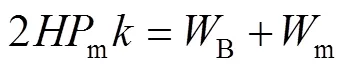
式中：為一個(gè)折疊的半波長(zhǎng)；m為平均壓縮載荷；為有效壓縮行程系數(shù)，通常取0.7～0.75[15]，取=0.75。

單個(gè)折疊單元在折疊的過(guò)程中會(huì)產(chǎn)生3條彎曲鉸鏈，如圖8所示，鉸鏈轉(zhuǎn)動(dòng)的角度θ分別為π/2、π和π/2。將彎曲鉸鏈的能量耗散相加得到彎曲能，見(jiàn)式（3）。

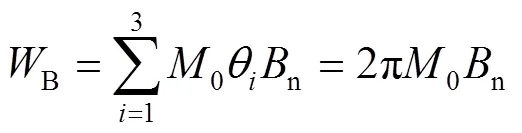
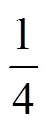
圖8 彎曲的能量耗散

Fig.8 Energy dissipation of bending

膜能是通過(guò)對(duì)膜拉伸和壓縮的面積進(jìn)行積分得到的。Zhang等[17]把零級(jí)SSF蜂窩劃分成3種基本單元：角單元、“十”字形單元和“T”形單元，如圖9所示，膜能的計(jì)算式分別見(jiàn)式（4）—（6）[17]。

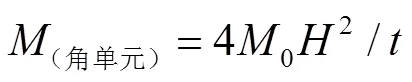
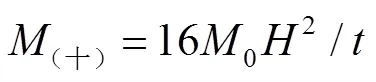
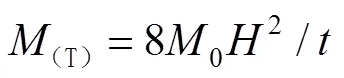
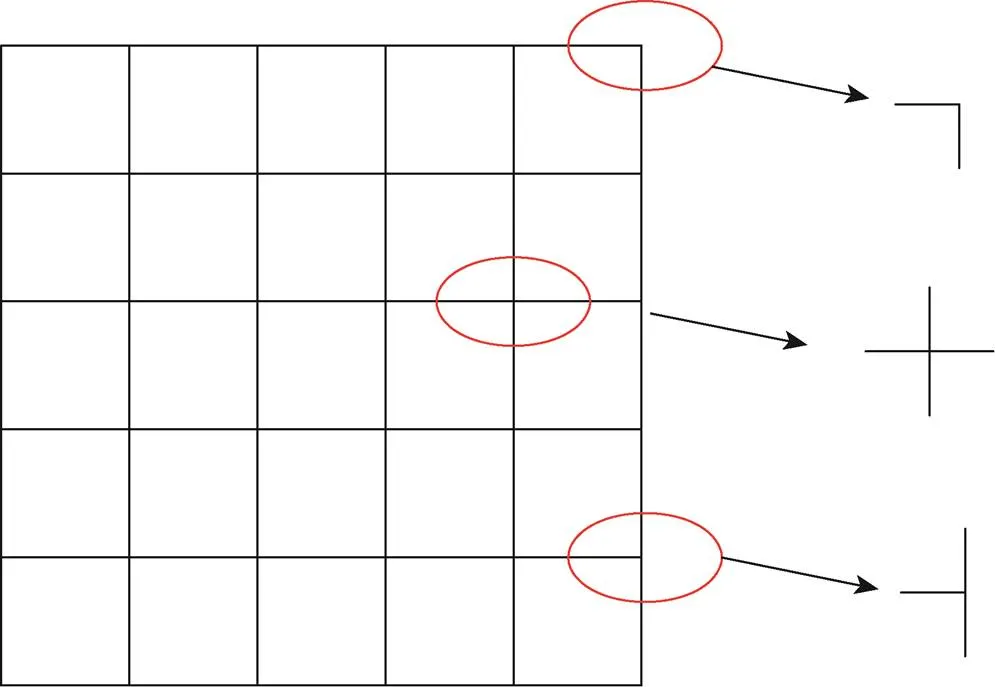
圖9 零級(jí)正方形自填充蜂窩的折疊單元示意圖

如圖10所示，一級(jí)SSF蜂窩在零級(jí)蜂窩的基礎(chǔ)上，增加了“K”形單元和六面板角單元兩種基本折疊單元，膜能的計(jì)算式見(jiàn)式（7）—（9）[18]，式中為45°。

圖10 一級(jí)正方形自填充蜂窩的折疊單元示意圖

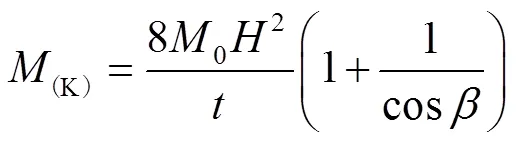
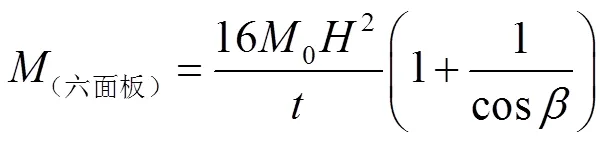
因此，SSF蜂窩膜能的通用計(jì)算公式為：

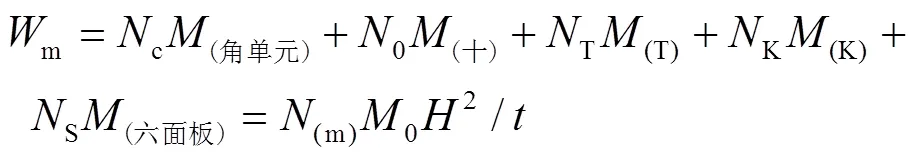
式中：c、0、T、K和S分別為角單元、“十”字形單元、“T”形單元、“K”形單元和六面板角單元的個(gè)數(shù)；（m）為膜能的系數(shù)函數(shù)，是由基本折疊單元的個(gè)數(shù)決定。

將式（3）和式（9）代入式（2）中，可以得到：

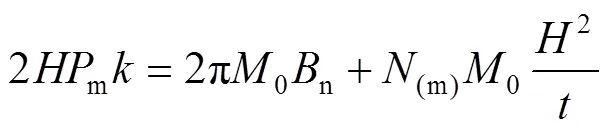
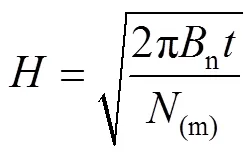
將式（11）代入式（10）中可以得到SSF蜂窩在異面下所承受的平均載荷為：

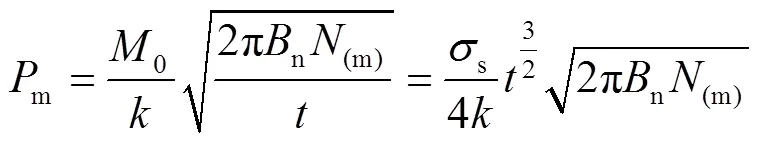
設(shè)SSF蜂窩的承載面積為，準(zhǔn)靜態(tài)平臺(tái)應(yīng)力的計(jì)算式為：

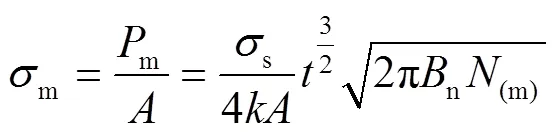
當(dāng)SSF蜂窩在1和3方向上的胞元數(shù)量均為11時(shí)，滿足陣列最少胞元數(shù)目的要求[19]。重復(fù)上述過(guò)程，可以得到0—5級(jí)正方形自填充蜂窩準(zhǔn)靜態(tài)平臺(tái)應(yīng)力的理論模型，即當(dāng)=0時(shí)，m=4.93s(/)1.5；當(dāng)=1時(shí)，m=18.07s(/)1.5；當(dāng)=2時(shí)，m=28.89s(/)1.5；當(dāng)=3時(shí)，m=38.17s(/)1.5；當(dāng)=4時(shí)，m=46.24s(/)1.5；當(dāng)=5時(shí)，m=53.35s(/)1.5。

2.2 理論模型的驗(yàn)證

從圖11中可以看出，SSF蜂窩在不同壁厚邊長(zhǎng)比/下的準(zhǔn)靜態(tài)平臺(tái)應(yīng)力的理論值與仿真值具有很好的一致性。說(shuō)明在允許的誤差范圍內(nèi)，所推導(dǎo)的理論模型具有可靠性，可以有效預(yù)測(cè)SSF蜂窩的異面準(zhǔn)靜態(tài)平臺(tái)應(yīng)力。

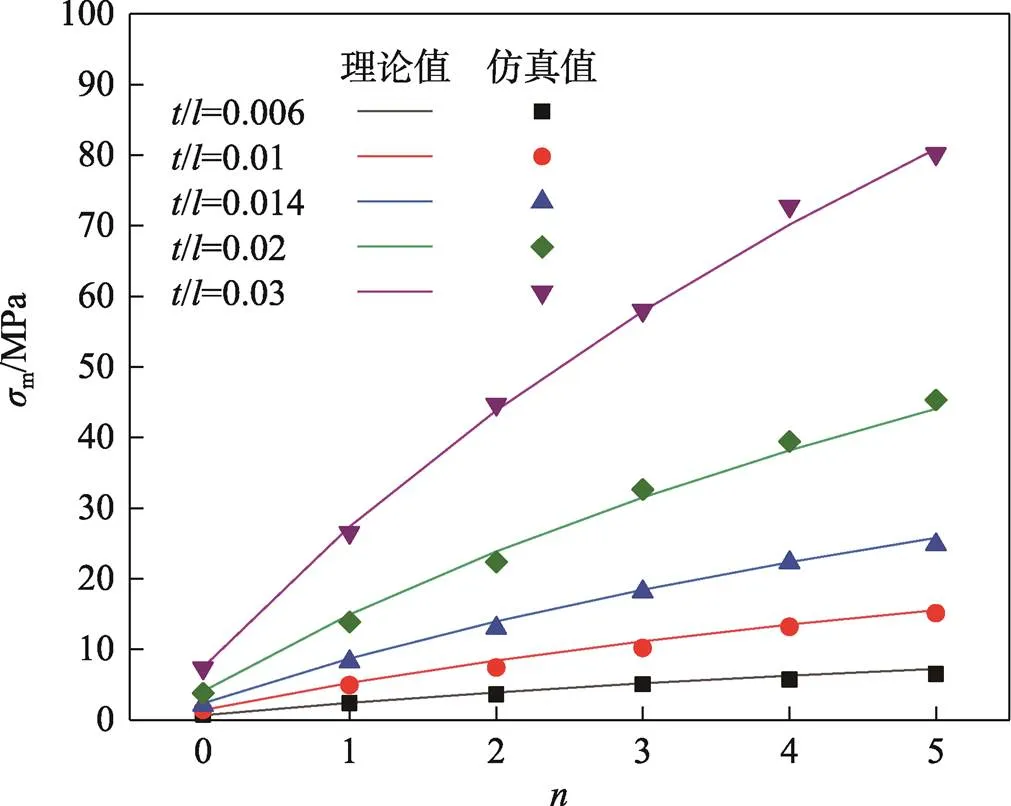
圖11 準(zhǔn)靜態(tài)平臺(tái)應(yīng)力的理論與仿真值

3 動(dòng)態(tài)平臺(tái)應(yīng)力

已有研究表明[20]，蜂窩在異面動(dòng)態(tài)沖擊下會(huì)產(chǎn)生動(dòng)態(tài)增強(qiáng)現(xiàn)象，其動(dòng)態(tài)平臺(tái)應(yīng)力會(huì)顯著大于準(zhǔn)靜態(tài)平臺(tái)應(yīng)力。本節(jié)將基于數(shù)值模擬分析來(lái)研究SSF蜂窩動(dòng)態(tài)平臺(tái)應(yīng)力σ的影響因素。

3.1 沖擊速度的影響

以一級(jí)SSF蜂窩為例來(lái)研究沖擊速度對(duì)蜂窩動(dòng)態(tài)平臺(tái)應(yīng)力1的影響。表1給出了蜂窩在不同/和下的1值，并基于最小二乘法擬合得到如圖12所示的1-曲線。從圖12中可以看出，SSF蜂窩的1與2呈線性關(guān)系，滿足關(guān)系式（14），符合Reid等[21]提出的一維沖擊波模型。在/一定時(shí)，=200 m/s的1值在=3 m/s的基礎(chǔ)上提高了163%～275%，說(shuō)明SSF蜂窩在高速?zèng)_擊載荷下具有更高的動(dòng)態(tài)平臺(tái)應(yīng)力。

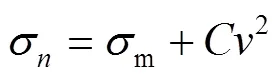
式中：2為慣性效應(yīng)引起的動(dòng)態(tài)增強(qiáng)；為動(dòng)態(tài)增強(qiáng)系數(shù)，列于表1的最后1列。

3.2 壁厚邊長(zhǎng)比的影響

從表1中可以看出，不同的壁厚邊長(zhǎng)比對(duì)應(yīng)著不同的動(dòng)態(tài)增強(qiáng)系數(shù)，為了研究這種相關(guān)性，基于最小二乘法擬合得到-/曲線，如圖13所示，并得到了動(dòng)態(tài)增強(qiáng)系數(shù)的經(jīng)驗(yàn)公式（15），這與Ruan等[22]的結(jié)論是一致的。

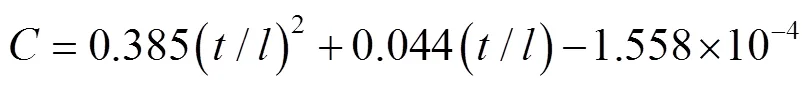
結(jié)合式（14）—（15），得到一級(jí)SSF蜂窩的動(dòng)態(tài)平臺(tái)應(yīng)力1公式為：

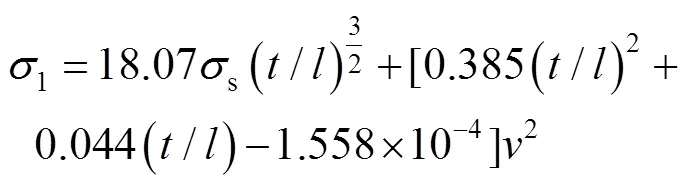
當(dāng)沖擊速度一定時(shí)，式（16）可以近似用冪指函數(shù)來(lái)代替，即：

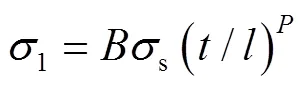
式中：為擬合系數(shù)；為指數(shù)。不同的沖擊速度下對(duì)應(yīng)著不同的和。

基于表達(dá)式（17）擬合表1中的數(shù)據(jù)，得到如圖14所示的1-/曲線。從圖14中可以看出，仿真值與經(jīng)驗(yàn)公式具有很好的一致性。在一定時(shí)，一級(jí)SSF蜂窩的1與/呈冪指數(shù)關(guān)系，/=0.05的1值是/0.006的23.27倍，說(shuō)明大的壁厚邊長(zhǎng)比能夠使SSF蜂窩承受更高的異面動(dòng)態(tài)平臺(tái)應(yīng)力。

表1 一級(jí)正方形自填充蜂窩在異面沖擊載荷下的動(dòng)態(tài)平臺(tái)應(yīng)力值

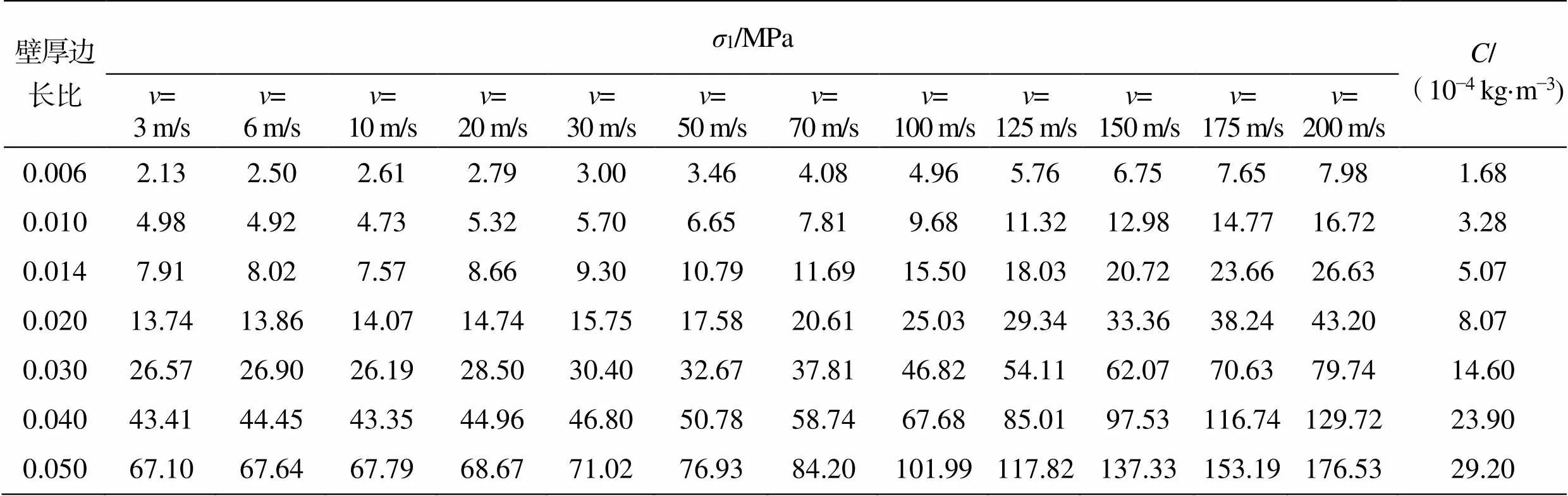
Tab.1 Dynamic plateau stresses of 1 order square self-filled honeycomb under out-of-plane impact

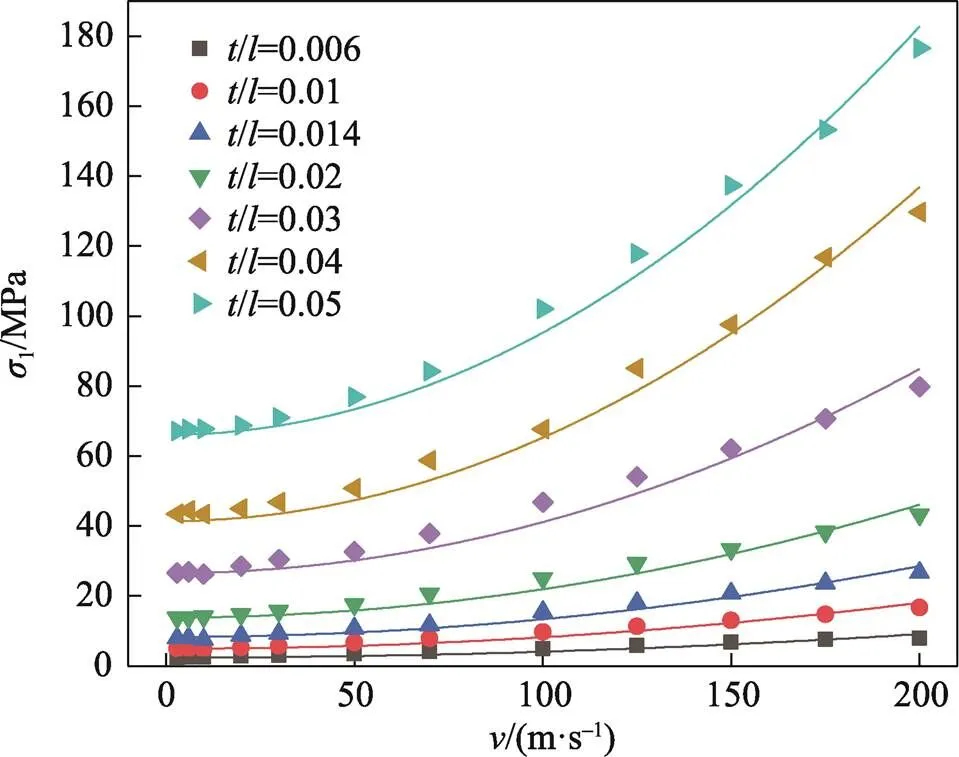
圖12 一級(jí)正方形自填充蜂窩的σ1-v曲線

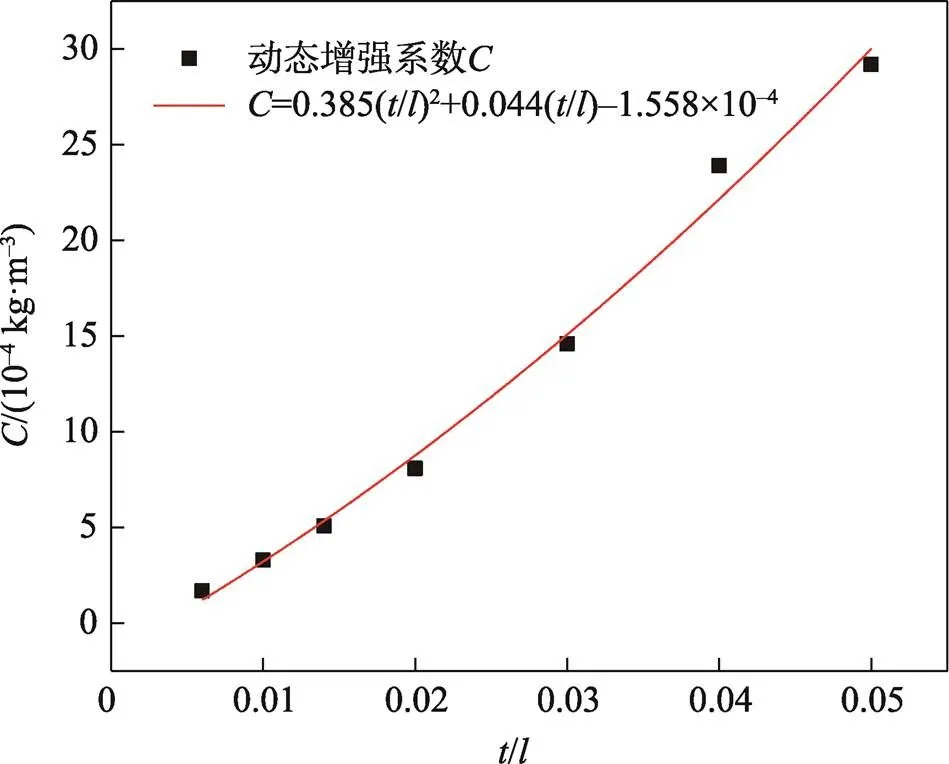
圖13 擬合得到的一級(jí)正方形自填充蜂窩的C-t/l曲線

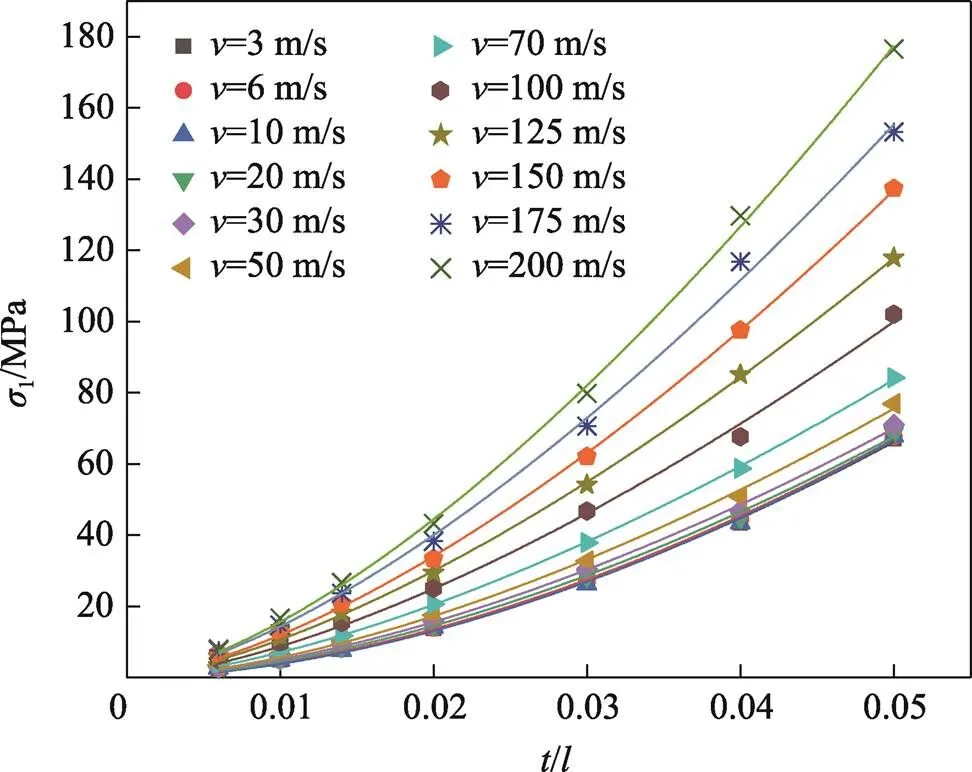
圖14 一級(jí)正方形自填充蜂窩的σ1-t/l曲線

3.3 自填充級(jí)數(shù)的影響

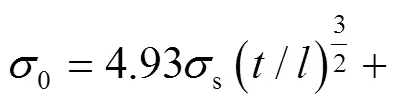
圖15為0—5級(jí)SSF蜂窩在/為0.02時(shí)的σ-曲線。從圖15可直觀看出，當(dāng)一定時(shí)，蜂窩的動(dòng)態(tài)平臺(tái)應(yīng)力隨自填充級(jí)數(shù)逐級(jí)遞增，其增長(zhǎng)率隨自填充級(jí)數(shù)逐級(jí)遞減。在自填充級(jí)數(shù)由0變?yōu)?時(shí)，動(dòng)態(tài)平臺(tái)應(yīng)力的增長(zhǎng)率最大，在自填充級(jí)數(shù)由4變?yōu)?時(shí)，動(dòng)態(tài)平臺(tái)應(yīng)力的增長(zhǎng)率最小，這與經(jīng)驗(yàn)公式中的動(dòng)態(tài)增強(qiáng)系數(shù)的變化規(guī)律是相吻合的。

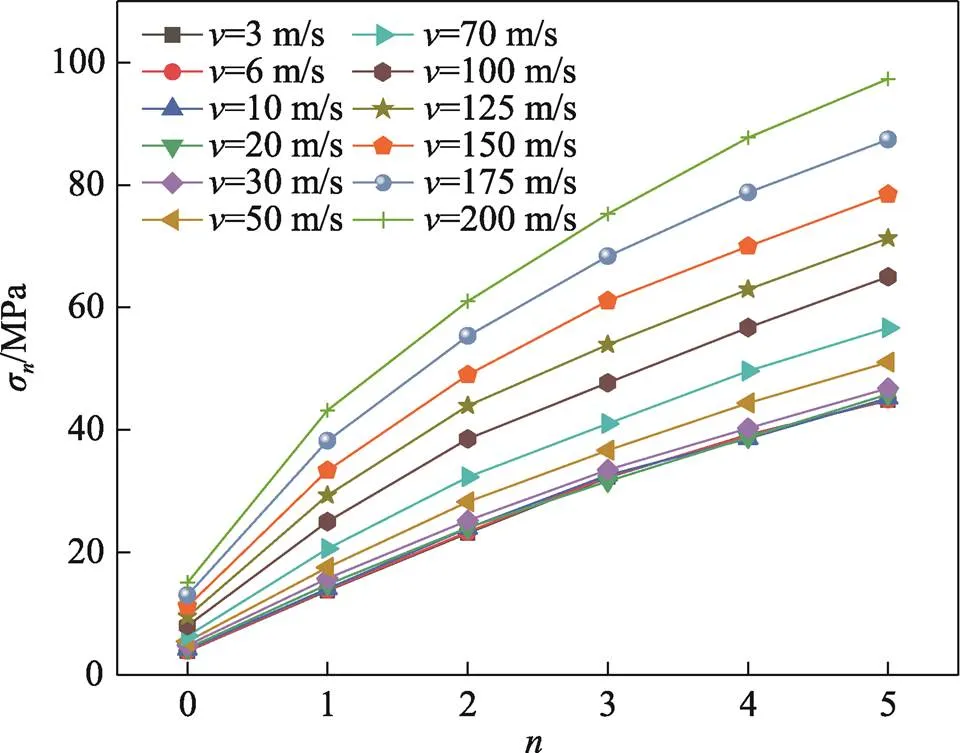
圖15 正方形自填充蜂窩的σn-n曲線

4 結(jié)語(yǔ)

本文主要基于簡(jiǎn)化的超折疊單元理論和有限元數(shù)值模擬，得到了SSF蜂窩異面平臺(tái)應(yīng)力的理論模型和經(jīng)驗(yàn)公式，具體結(jié)論如下：

1）通過(guò)對(duì)蜂窩樣品進(jìn)行準(zhǔn)靜態(tài)壓縮試驗(yàn)，將試驗(yàn)結(jié)果與仿真結(jié)果進(jìn)行對(duì)比，變形模式與應(yīng)力-應(yīng)變曲線都具有很好的一致性，由此證明了有限元仿真模型的可靠性。

2）基于簡(jiǎn)化的超折疊單元理論推導(dǎo)了SSF蜂窩準(zhǔn)靜態(tài)平臺(tái)應(yīng)力的理論模型，對(duì)比分析了仿真值與理論值，兩者都很吻合，說(shuō)明理論模型是準(zhǔn)確的。

3）SSF蜂窩的動(dòng)態(tài)平臺(tái)應(yīng)力與速度的平方呈線性關(guān)系，與壁厚邊長(zhǎng)比呈冪指函數(shù)關(guān)系，在大的壁厚邊長(zhǎng)比和高速?zèng)_擊下，具有更高的動(dòng)態(tài)平臺(tái)應(yīng)力。

4）SSF蜂窩的動(dòng)態(tài)平臺(tái)應(yīng)力增長(zhǎng)率隨自填充級(jí)數(shù)的增加而趨緩。當(dāng)由0變?yōu)?時(shí)，動(dòng)態(tài)平臺(tái)應(yīng)力的增長(zhǎng)率最大。通過(guò)數(shù)值模擬計(jì)算結(jié)果，得到了0—5級(jí)SSF蜂窩動(dòng)態(tài)平臺(tái)應(yīng)力的經(jīng)驗(yàn)公式。

[1] 馬芳武, 孫昊, 梁鴻宇, 等. 自相似分層蜂窩結(jié)構(gòu)多碰撞工況耐撞性研究[J]. 汽車工程, 2022, 44(6): 886-892.

MA Fang-wu, SUN Hao, LIANG Hong-yu, et al. Study on Crashworthiness of Self-Similar Hierarchical Honeycomb Structure under Multiple Collision Conditions[J]. Automotive Engineering, 2022, 44(6): 886-892.

[2] ALPHONSE M, RAJA V, KRISHNA V, et al. Mechanical Behavior of Sandwich Structures with Varying Core Material-a Review[J]. Materials Today Proceedings, 2021, 44(1): 3751-3759.

[3] XU Gang, WANG Zhong-gang, LI Zhen-dong, et al. Theoretical and Numerical Analyses on Mechanical Performance of Octagonal Honeycomb Structures Subjected to Out-of-Plane Compression[J]. Mechanics of Advanced Materials and Structures, 2020, 27(17): 1461-1472.

[4] ALTIN M, ACAR E, GULER M. Crashworthiness Optimization of Hierarchical Hexagonal Honeycombs under Out-of-Plane Impact[J]. ARCHIVE Proceedings of the Institution of Mechanical Engineers Part C Journal of Mechanical Engineering Science, 2020, 235(6): 203-210.

[5] LI Zhi-gang, WANG J, LI M, et al. Theoretical Analysis and Numerical Simulation of Square Honeycombs[J]. Journal of Physics Conference Series, 2021, 1777(1): 1-8.

[6] ZHANG Yong, CHEN Teng-teng, XU Xiang, et al. Out-of-Plane Mechanical Behaviors of a Side Hierarchical Honeycomb[J]. Mechanics of Materials, 2019, 140: 103227.

[7] LIU Qiang, FU Jie, MA Jing-bo, et al. Axial and Lateral Crushing Responses of Aluminum Honeycombs Filled with EPP Foam[J]. Composites Part B Engineering, 2017, 130: 236-247.

[8] 彭琦. 泡沫填充類蜂窩夾層結(jié)構(gòu)耐撞性分析[D]. 宜昌: 三峽大學(xué), 2020: 15-46.

PENG Qi. Crashworthiness Analysis of Foam-Filled Honeycomb-Like Sandwich Structure[D]. Yichang: China Three Gorges University, 2020: 15-46.

[9] ZHANG L W, BAI Z H, BAI F H. Crashworthiness Design for Bio-inspired Multi-cell Tubes with Quadrilateral, Hexagonal and Octagonal Sections[J]. Thin-Walled Structures, 2018, 122(1): 42-51.

[10] WU Su-zhen, ZHENG Gang, SUN Guang-yong, et al. On Design of Multi-Cell Thin-Wall Structures for Crashworthiness[J]. International Journal of Impact Engineering, 2016, 88: 102-117.

[11] ZHANG Yong, LU Ming-hao, WANG C H, et al. Out-of-Plane Crashworthiness of Bio-Inspired Self- Similar Regular Hierarchical Honeycombs[J]. Composite Structures, 2016, 144: 1-13.

[12] SUN D Q, SUN Y J, BEN J C, et al. Energy Absorption Characteristics of Circular-celled Honeycombs under In- plane Quasi-static Compressive Loadings[J]. International Journal of Materials Research, 2021, 112(7): 565-577.

[13] GB/T 16865—2013, 變形鋁、鎂及其合金加工制品拉伸試驗(yàn)用試樣及方法[S].

GB/T 16865—2013, Test Pieces and Method for Tensile Test for Wrought Aluminium and Magnesium Alloys Products[S].

[14] CHEN W, WIERZBICKI T. Relative Merits of Single-cell, Multi-Cell and Foam-filled Thin-Walled Structures in Energy Absorption[J]. Thin-Walled Structures, 2001, 39(4): 287-306.

[15] 于鵬山, 劉志芳, 李世強(qiáng). 新型仿生蜂窩結(jié)構(gòu)的設(shè)計(jì)與耐撞性能分析[J]. 高壓物理學(xué)報(bào), 2022, 36(1): 149-160.

YU Peng-shan, LIU Zhi-fang, LI Shi-qiang. Design and Crashworthiness Analysis of New Bionic Honeycomb Structure[J]. Chinese Journal of High Pressure Physics, 2022, 36(1): 149-160.

[16] 趙國(guó)偉, 白俊青, 祁玉峰, 等. 異面沖擊下金屬蜂窩結(jié)構(gòu)平均塑性坍塌應(yīng)力模型[J]. 振動(dòng)與沖擊, 2016, 35(12): 50-54.

ZHAO Guo-wei, BAI Jun-qing, QI Yu-feng, et al. Average Plastic Collapse Stress Model of Metallic Honeycomb Structure under Out-of-Plan Impact Load[J]. Journal of Vibration and Shock, 2016, 35(12): 50-54.

[17] ZHANG Xiong, CHENG G, ZHANG Hui. Theoretical Prediction and Numerical Simulation of Multi-Cell Square Thin-Walled Structures[J]. Thin-Walled Structures, 2006, 44(11): 1185-1191.

[18] TRAN T, HOU Shu-juan, HAN Xu, et al. Theoretical Prediction and Crashworthiness Optimization of Multi-Cell Triangular Tubes[J]. Thin-Walled Structures, 2014, 82(12): 183-195.

[19] WANG Zhong-gang, SHI Chong, DING San-san, et al. Crashworthiness of Innovative Hexagonal Honeycomb-Like Structures Subjected to Out-of-Plane Compression[J]. Journal of Central South University, 2020, 27(2): 621-628.

[20] XU Shan-qing, BEYNON J H, RUAN Dong, et al. Strength Enhancement of Aluminium Honeycombs Caused by Entrapped Air under Dynamic Out-of-Plane Compression[J]. International Journal of Impact Engineering, 2012, 47: 1-13.

[21] REID S R, PENG C. Dynamic Uniaxial Crushing of Wood[J]. International Journal of Impact Engineering, 1997, 19(5/6): 531-570.

[22] RUAN D, LU G, WANG B, et al. In-Plane Dynamic Crushing of Honeycombs―a Finite Element Study[J]. International Journal of Impact Engineering, 2003, 28(2): 161-182.

Out-of-plane Plateau Stress of Square Self-filled Honeycomb Structure

SUN De-qiang1, GE Feng1, ZHANG Chao2, CUI Yan-yan1, BEN Jin-cui1, CHANG Lu1, GAO Lu-lu1, WANG Qian1

(1. a. Key Lab of Functional Printing and Transport Packaging of China National Light Industry b. National Demonstration Center for Experimental Light Chemistry Engineering Education c. 3S Research Institute of Novel Packaging Science and Technology, Shaanxi University of Science and Technology, Xi'an 710021, China; 2. Xi'an XD Transformer Co., Ltd., Xi'an 710077, China)

The work aims to promote the rational use of square self-filled honeycombs by studying the change rules of their out-of-plane plateau stresses with impact velocity, ratio of cell wall thickness to side length and self-filling order. ANSYS/LS-DYNA was used to establish the finite element model based on cells array for the out-of-plane impact analysis of square self-filled honeycombs. The out-of-plane compression test and corresponding simulation analysis were carried out on the square honeycomb with self-filling order of 0 to prove the reliability of the finite element model. Based on the simplified super folded element theory, the theoretical quasi-static plateau stress model of square self-filled honeycomb was established and verified by the simulation results. The square self-filled honeycomb higher dynamic plateau stress with increasing ratio of cell wall thickness to side length and impact velocity. When the self-filling order changed from 0 to 1, the growth rate of the dynamic plateau stress was the largest. When other factors are fixed, the out-of-plane dynamic plateau stress of square self-filled honeycomb has a linear relation with the square of velocity and a power function relation with the ratio of cell wall thickness to side length, and the growth rate decreases gradually with increasing self-filling order. Based on the finite element simulation, the empirical formulas of dynamic plateau stress are obtained for the square self-filled honeycomb with different self-filling orders.

square self-filled honeycomb; out-of-planeimpact; finite element simulation; plateau stress

TB484

A

1001-3563(2023)17-0269-07

10.19554/j.cnki.1001-3563.2023.17.033

2022-11-17

國(guó)家自然科學(xué)基金（51575327）；國(guó)家級(jí)一流專業(yè)建設(shè)項(xiàng)目（包裝工程2022）

責(zé)任編輯：曾鈺嬋