彈性地基梁板的徑向基函數逼近求解方法

林軍志,楊 笛,徐績青,3

(1. 重慶交通大學 河海學院,重慶 400074; 2. 山區公路水運交通地質減災重慶市教委重點實驗室,重慶 400074; 3. 重慶交通大學 國家內河航道整治工程技術研究中心 水利水運工程教育部重點實驗室,重慶 400074)

0 引 言

在工程中因地基變形而導致建筑物的損壞是不可無視的,因此與土體接觸的結構應按彈性地基梁和彈性地基板來考慮。筆者以Winkler模型為基礎,假設地基表面任一點的沉降與該點單位面積上的壓力成正比,建立了撓度微分方程式和邊界條件。

目前針對彈性地基梁板的撓度求解研究成果頗豐,如經典的Navier彈性地基板雙三角級數解[1],該方法是將荷載轉化為級數形式,將滿足邊界條件的試函數帶回微分方程得到撓度理論解;初參數法[2]是用撓度ω、轉角θ、彎矩M、剪力Q代替撓度函數中的4個參數,使積分常數具有明確的物理意義;處理變截面梁和邊荷載問題的鏈桿法[2],是用鏈桿力代替地基反力;楊維加[3]對彈性地基梁采用三角級數法進行求解;楊成永等[4]針對帶有脫空彈性地基梁問題采用傅里葉級數法進行求解。以上解析方法都是針對某些特定條件或規則形狀進行的求解,其計算形式較為復雜。

有限元方法在樣條函數空間尋找近似解,但對于求解高階偏微分問題所構造高階連續樣條函數基(高階連續單元)非常困難,且每次計算都需要剖分網格,計算工作量大。無網格方法[5]主要有滑動最小二乘法[6]、伽遼金法[7]、雜交邊界法[8]等,這些方法均是通過數值積分得到弱形式解。基于徑向基函數[9-14]的求解具有如下優點:表達與計算非常簡單、各向同性、任意多元函數都可用一元函數來描述、節約存儲成本、可以逼近幾乎所有的從各向同性問題中產生的函數。采用徑向基函數,結合加權余量法[15]中的配點法對線性方程組進行離散,通過笛拉克函數控制殘差可得到計算簡單、精度高、通用性強的強形式解。

1 撓度微分方程與邊界條件

1.1 彈性地基梁

域內微分方程的計算如式(1):

(1)

自然邊界條件如式(2):

W|x=0,l=0

(2)

本質邊界條件如式(3):

(3)

式中:EI為彈性地基梁的彎曲剛度,kN·m;k為彈性地基系數,kN/m3;b取單寬,m;l為寬度,m;q(x)為施加在彈性地基梁上的荷載,kN/m。

1.2 彈性地基板

域內微分方程的計算如式(4):

D?4W(x,y)+kW(x,y)=q(x,y)

(4)

自然邊界條件如式(5):

W|x=0,2a=0,W|y=0,2b=0

(5)

本質邊界條件如式(6):

(6)

式中:D為彈性地基板的彎曲剛度,kN·m;2a、2b分別為板的長和寬,m。

2 徑向基函數

筆者根據文獻[9-10],基于修正再生核逼近思想構造了局部緊支撐徑向基函數(該函數使離散插值矩陣具有帶疏性)及根據經驗改良后的Gauss公式,如式(7)～式(12)。這樣可以解決因數值計算中布點過密產生的病態矩陣問題。

φ(r)=(1-r)5×(1+5r+9r2+5r3+r4)

(7)

φ(r)=(1-r)6(6+36r+82r2+72r3+30r4+5r5)

(8)

φ(r)=(1-r)6(3+18r+35r2)

(9)

φ(r)=(1-r)7(5+35r+101r2+147r3+101r4+35r5+5r6)

(10)

φ(r)=(1-r)8(1+8r+25r2+32r3)

(11)

φ(r)=expcr2

(12)

需特別注意,若有r=d/dmax則以上函數應滿足式(13)。

(13)

3 徑向基函數配點法

3.1 加權余量配點法

已知基本微分方程式和邊界條件[15]:

(14)

式中:D、G分別為微分算子;d、g分別為不含函數的項;u為待求函數項;m為邊界條件數。

假設待定函數u的近似解為Ui,則有式(15):

(15)

式中:ai為待定系數;fi為形式確定的試函數項;n為試函數項的數目。

將近似解代入微分方程,則有內部殘量R1和邊界殘量R2[15]:

(16)

選用笛拉克函數作為權函數ωi(x),如式(17):

ωi(x)=δ(x-xi)=0,(x≠xi)

(17)

根據笛拉克函數的挑選性,控制殘差在一系列配點上xi=0,則有式(18)。

(18)

求解式(18),即可得到待定系數ai。

3.2 徑向基函數配點求解

取徑向基函數作為試函數,則撓度的近似解Ui[11]可由式(19)表達。

(19)

所求區域用n個節點離散。設P為區域內部nP個節點的集合;Q為邊界x方向上的nQ個節點集合;S為邊界y方向上的nS個節點集合;則有n=nP+nQ+nS。n個節點對應的未知撓度為n個,試函數數量與未知量數量相同,可建立n個線性方程組,如式(20)。

(20)

令特征矩陣A=[Φ(r)],系數矩陣α=[α1,α2,…,αn]T,待求矩陣U=[U1,U2,…,Un]T,則可簡化如式(21):

Aα=U

(21)

任意點的撓度近似解可表示為式(22):

[φ1(ri)φ2(ri) …φn(ri)]A-1U

(22)

梁、板方程的求解〔式(1)～式(6)〕一般分為兩種方法。

方法1:不求逆矩陣,以待定系數矩陣α為未知量求解。

方法2:求逆矩陣,以待求矩陣U作為未知量求解。

3.3 方法改進

在數值計算中,常規配點法往往會在邊界處產生嚴重振蕩[14],針對這一問題可利用本質邊界條件新增未知量,借鑒彈塑性靜力學的處理方法提出n個節點撓度和nQ+nS個邊界點撓度的二階偏導量聯合插值的近似解,如式(23),明確附加了未知量的物理意義。

(23)

式(23)對于徑向基函數的高階連續性有一定要求,為了避免徑向基函數高階求導后形成的特征矩陣條件數增大,應對式(23)進行簡化。

分別采用線性無關的輔助徑向基函數βi(ri),γi(ri)來代替高階偏導項,如式(24)。

(24)

式(24)中:右邊第1項代表n個節點的撓度;第2項代表在邊界點上對x方向的曲率;第3項代表在邊界點上對y方向的曲率。

此時式(24)可寫作式(25):

(25)

n+nQ+nS個待定系數的n個方程組為超定解,因此為滿足一一對應關系,構造了附加未知量、矩陣A的附加行。數值計算中為降低方程組求解難度,從減小誤差思想出發,構建附加未知量與本質邊界條件等價可以使方程組的附加行列成為類單位陣。改造后的矩陣A及待求矩陣U如式(26)、 式(27):

n個節點對應n+nQ+nS個未知數,建立了n+nQ+nS個線性方程組,其中Vi,Zi為附加未知量。Vi表示為邊界點在x方向上撓度二階偏導量,即x方向的曲率;Zi表示為邊界點在y方向上撓度二階偏導量,即y方向的曲率。得到的近似解如式(28):

(26)

U=[U1…UnV1…VnQZ1…ZnS]T

(27)

[φ1(ri) …φn(ri)β1(ri) …βnQ(ri)γ1(ri) …γnS(ri)]A-1U

(28)

4 算法實施

1)建立4階偏微分方程和邊界條件方程;

2)在規定區域合理均勻配點,并求得個節點之間的距離及其影響半徑;

3)選取各線性無關的徑向基函數作為主函數和輔助函數構造近似解Ui;

4)方法1:根據各節點位置結合邊界條件構造特征矩陣A使得附加未知量具有物理意義;

方法2:根據各節點位置結合邊界條件構造特征矩陣A,使得附加未知量具有物理意義并求得逆矩陣B=A-1;

5)對近似解Ui求4階偏導;

6)方法1:將近似解Ui和4階偏導帶入微分方程中,并針對邊界點改變該行的微分方程使其滿足自然邊界條件。顯然具有公因子[a1, …,anb1, …,bnQc1,…,cnS]T;

方法2:將近似解和4階偏導函數帶入微分方程中,并通過化零置一的方法使其滿足自然邊界條件。顯然具有公因子[U1, …,UnV1, …,VnQZ1,…,ZnS]T;

7)方法1:利用A附加行的意義構造方程組,滿足微分方程和本質邊界條件;

方法2:由于附加未知量與本質邊界條件等價,因此在聯立方程時,式(3)、式(5)無需再次計算2階偏導式,而是構建類單位陣滿足邊界條件。若以第一個邊界點x方向曲率為例,如式(29):

(29)

轉換為式(30):

(30)

8)方法1:聯立方程組求得未知系數并帶回式(24),求得近似解Ui;

方法2:聯立方程組直接求得未知量Ui。

5 算例分析

5.1 彈性地基梁的撓度分析

算例1:假設一個兩端簡支的彈性地基梁,受均布荷載作用q=2 kN/m;簡支梁長度為L=4 m;EI=2.5×106kN·m2;地基彈性系數k=4×104kN/m3。如圖1。

圖1 彈性地基梁受均布荷載Fig. 1 Elastic foundation beam subjected to uniformly distributed load

已知彈性地基梁的撓度微分方程與邊界條件為式(1)～式(3),可得到理論解,如式(31):

(31)

(32)

(33)

則無量綱撓度理論解如式(34):

(34)

利用徑向基函數配點逼近的方法進行求解,選用文獻[10]提出的一維6階連續函數作為主函數和一維4階連續函數作為輔助函數。一維梁結構不存在y方向的曲率,因此構造出近似解Ui和矩陣A。

取節點間距為0.05均勻布點,則一共有n=21個節點,其中兩個邊界點nQ=2。采用方法一直接聯立式(1)～式(3),求解得到未知系數代入近似解的撓度值如圖2。從數學精度方面考慮全局相對誤差1.38%;工程上為滿足安全性原則,一般考慮最大撓度變形點。由圖2可見:最大撓度變形發生在跨中0.012 5 m處,與理論解相比,其相對誤差僅為0.084%,優于最小滑動二乘解。

圖2 彈性地基梁受均布荷載撓度分析Fig. 2 Deflection analysis of elastic foundation beam subjected to the uniformly distributed load

5.2 彈性地基板的撓度分析

5.2.1 算例2

若有一塊簡支彈性地基板,板長為10 m(即a=5),板寬為10 m(即b=5);板的彎曲剛度為D=2.5×104kN·m;地基彈性系數為k=104kN/m3;板上受到均布荷載為q=2 kN/m2,如圖3。

圖3 彈性地基板受均布荷載Fig. 3 Elastic foundation beam and plate subjected to the uniformly distributed load

已知彈性地基板的撓度微分方程與邊界條件為式(4)～式(6),則可得到理論解,如式(35):

(35)

利用徑向基函數配點逼近的方法進行求解,選用文獻[10]提出的三維4階連續函數作為主函數,文獻[9]構造的三維4階連續函數作為輔助函數和文獻[10]的三維6階連續函數作為輔助函數構造出近似解Ui和矩陣A。

板面上4個角點同時考慮對x、y兩個方向求曲率,利用方法2求出逆矩陣B,利用附加未知量的意義構造一個類似單位矩陣的大小為2m行n+2m列的矩陣M(M=[RT]),R為2m行n列的零矩陣,T為2m行2m列的單位矩陣。使其乘以n+2m個未知量,并通過化零置一轉化成未知系數與本質邊界條件等價的未知量。取節點間距為0.25,均勻布點,則一共有n=1 681個節點,其中邊界點160個。

得到的各撓度值如圖4。

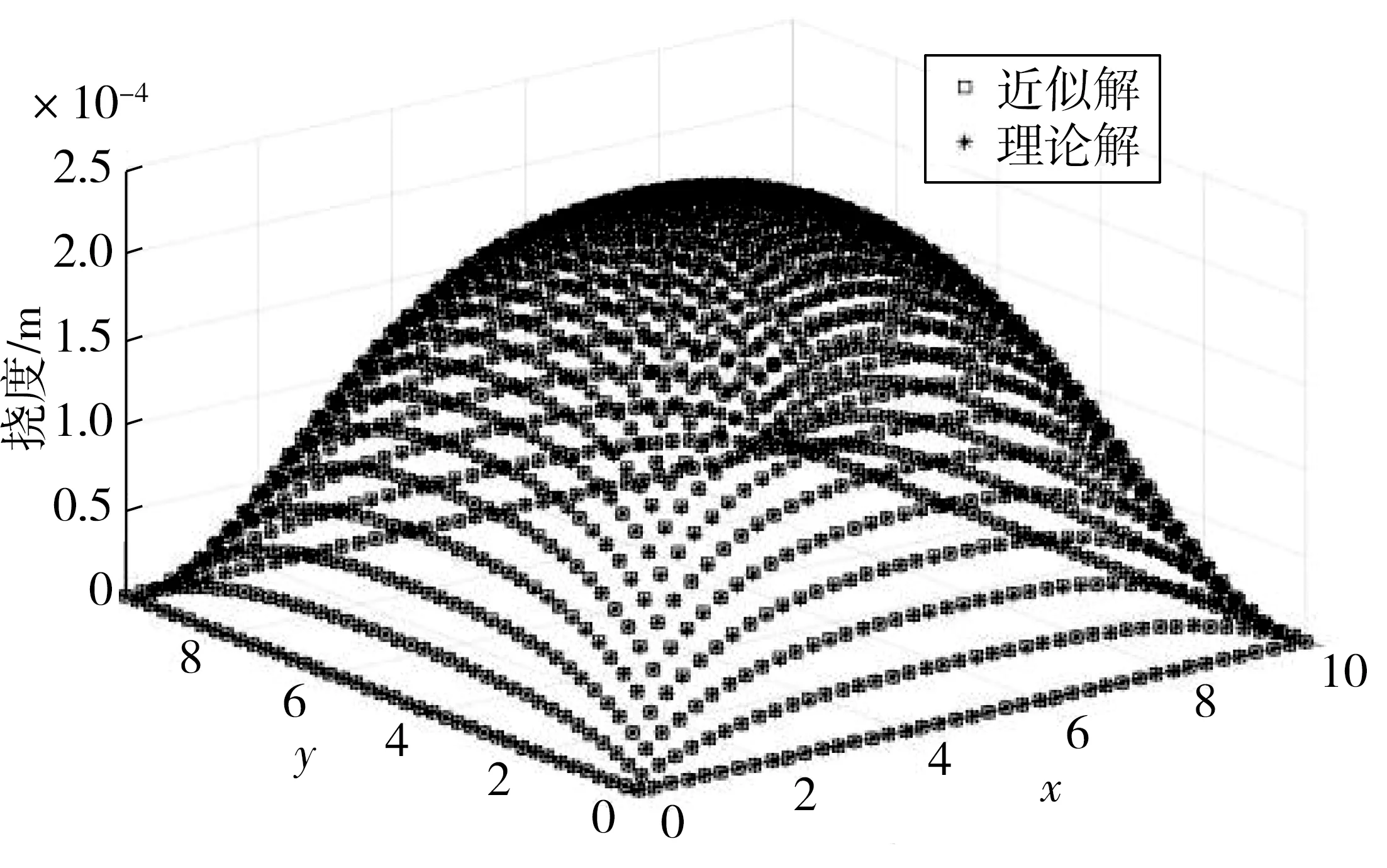
圖4 彈性地基板受到均布荷載的撓度分析Fig. 4 Deflection analysis of elastic foundation beam and plate subjected to the uniformly distributed load

板最大撓度變形發生在板中央,近似解為2.42×10-4m,略大于理論解,撓度最大值相對誤差為0.012%。此時逆矩陣的求逆精度為3.05×10-5,從工程實際而言效果較好;節點全局平均相對誤差為0.46%,從數學層面考慮精度較好。

5.2.2 算例3

若有一塊四邊簡支的正方形薄板,幾何尺寸為1 m×1 m(即a=0.5,b=0.5)。板的彈性模量為E=2.1×1010Pa,泊松比為μ=0.3,地基彈性系數為k=4.9×104kN/m3,板上受到均布荷載為q=1 kN/m2。

利用徑向基函數配點逼近方法進行求解,選用改良后的Gauss函數作為主函數,輔助函數為式(8)、 式(9)分別對x、y方向的曲率。在滿足域內微分方程和邊界條件的情況下構造出近似解Ui,采用方法二求逆矩陣B,并以待求矩陣U作為未知量建立方程組。

取節點間距為0.025,共有n=1 681個節點,其中160個邊界點。由于地基反力變大,撓度最大值不會發生在板中央,由此得到撓度結果[7],見圖5。與理論解對比,撓度最大值相對誤差為0.178%,與整體相對誤差嚴重不匹配,這是因為Gauss函數求逆精度低。

圖5 馬鞍形撓度值(調整前)Fig. 5 Saddle-type deflection value (before the adjustment)

故從代數方面考慮,讓邊界點除了滿足邊界條件外同時滿足邊界微分方程,如式(36),通過改變矩陣大小及排列來提高精度。

(36)

主函數與輔助函數不變,此時x、y兩個方向的曲率都用式(8)表示,4階偏導用式(9)表示,構造出近似解Ui和矩陣A如式(37)、式(38),其余步驟與方法2相同。

(37)

(38)

調整后的撓度值如圖6。與理論解對比,其整體相對誤差明顯減小,撓度最大值的相對誤差為0.013%,比調整前提高10倍,精度滿足工程需要;板中心撓度相對誤差為0.013 5%,與雜交邊界法相當。

圖6 馬鞍形撓度值(調整后)Fig. 6 Saddle-type deflection value (after the adjustment)

6 結 論

筆者為求解彈性地基梁和彈性地基板的撓度值,采用了徑向基函數配點逼近的方法,得出如下結論:

1)徑向基函數配點法形式簡單,無網格化,計算方便,求解精度高;

2)在構建矩陣A時,可根據邊界條件編寫附加行,使得附加未知量具有一定的物理意義,從而通過簡化方程求解來減小誤差;

3)針對方程求解提出兩種算法:不求逆矩陣,以待定系數作為未知數進行求解;求逆矩陣,以撓度值作為未知數進行求解,根據矩陣求逆精度選擇算法;

4)參考緊支柱思想,改造了與全局支撐域相關聯的Gauss函數,使其無量綱化,根據經驗確定其參數c=-23.026;

5)為解決改造后的Gauss函數求逆性差的問題,可利用邊界微分方程建立輔助函數,以提高求解精度。