廣義(3+1)維KdV方程的lump解、相互作用解和呼吸子解

于明惠, 王云虎

(上海海事大學 理學院, 上海 201306)

0 引 言

非線性演化方程在非線性科學中有著重要的應用,它為描述流體力學、光纖、等離子體物理等科學領域中的一些非線性現象提供了有效的模型[1-2],例如Korteweg-de Vries(KdV)方程可用于模擬分層流體中的內波和等離子體中的離子聲波[3],Kadomtsev-Petviashvili(KP)方程可用于模擬長橫向擾動下流體中的弱色散波[4]．在孤子理論中,尋找非線性演化方程的精確解一直以來都是眾多學者關注的研究熱點,如孤立波解、lump解以及怪波解等[5-7]．目前,人們已經發現了許多有效求解非線性演化方程精確解的方法,如反散射變換[1]、 B?ckland 變換[8]、Darboux變換[9]和雙線性方法[10]等．

雙線性方法是求解非線性演化方程精確解的一種重要方法,該方法的優點在于一旦將給定的非線性演化方程通過變量變換轉化為雙線性方程,則可通過直接求解雙線性方程得到給定的非線性演化方程的精確解．隨著雙線性方法的廣泛應用,眾多學者在此基礎上提出了各種直接求解方法．2015年,Ma(馬文秀)提出了一種直接構造雙線性可積方程lump解的方法,得到了(2+1)維KPI方程的lump解[11]．Zhang和Chen等[12-13]進一步發展完善了該方法,并利用該方法在KP方程中首次發現了由共振孤子所激發產生的怪波,發現了線孤子和lump波相互作用產生的“聚變”和“裂變”現象．此后, 國內外學者在這一領域開展了廣泛的工作,發現了越來越多的lump-扭結解、lump-線孤子解等[14-30]．

高維非線性演化方程由于可以為探究物理現象提供更多的信息而受到廣泛關注[31-33]．本文主要研究如下的廣義(3+1)維KdV方程[34]:

(1)

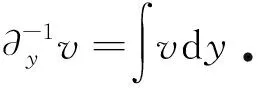
當δ=0時,方程(1)可退化為如下(2+1)維KdV方程:

(2)

文獻[34]證明了方程(2)是Painlevé可積的,并利用雙線性方法得到了其多實孤子解和多復孤子解．文獻[37]利用相容tanh展開法得到其共振解、孤子與橢圓余弦波的相互作用解,文獻[38]基于雙線性方法得到了其lump解、相互作用解和怪波解．

當α=3,β=0和γ=0時,方程(2)進一步轉化為

(3)

方程(3)由Boiti等[35]首次給出,可用于描述不可壓縮流體的動力學行為并已被證明具有Lax對、無窮多守恒律．文獻[39]利用雙線性方法、tanh-coth方法以及冪函數法得到了該方程的包括多孤子解在內的行波解．

當y=x時,方程(3)即為經典的(1+1)維KdV方程[40]:

vt+6vvx+vxxx=0．

(4)

文獻[34]利用Painlevé分析和雙線性方法研究了方程(1)可積性檢驗和多孤子解;文獻[41]利用雙線性方法和Riemann-theta函數研究了方程(1)的雙線性形式、N-孤子解、呼吸子解、混合解和擬周期波解．本文利用方程(1)的雙線性形式,通過擬設的方法直接構造其lump解、相互作用解和呼吸子解．本文的主要結構如下:第1節中,通過對雙線性方程中的f函數取3種不同的形式,分別得到了方程(1)的lump解、相互作用解和呼吸子解,證明了lump解的局域性,發現了lump波與線孤子的相互作用過程中的“聚變”和“裂變”現象,并利用圖形展示了解的動力學特征．第2節中,我們將給出一些結論．

1 Lump解、相互作用解和呼吸子解

為得到方程的雙線性形式,首先引入勢變換:

v=uy,

(5)

方程(1)變為

uty+uxxxy+αuxxuy+αuxuxy+βuxx+γuyy+δuzy=0．

(6)

再利用對數變換

(7)

可得方程(1)的雙線性形式:

(8)

其中f是關于空間變量x,y,z和時間變量t的函數,D是Hirota雙線性算子,其定義為[10]

其中n和m均為非負整數．

為得到方程(1)的lump解、相互作用解和呼吸子解,關鍵是構造雙線性方程(8)的解．由此,我們做如下假設:

f=g2+h2+keη+le-η+a11,

(9)

其中g,h和η分別具有如下形式:

(10)

其中ai(i=1,2,…,11),ki(i=1,2,3,4),k和l均為待定參數．

1.1 Lump解

基于文獻 [11],在函數(9)中取k=0,l=0并將其代入雙線性方程(8)中,利用符號計算軟件MAPLE,收集變量x,y,z,t的不同冪次系數,求解相應的代數方程組,可得參數a1～a11之間具有如下關系:

(11)

其中

(12)

且

由此,方程(1)的解可寫為

(13)

其中

(14)

且需滿足如下約束條件:

A3β< 0,

(15)

以確保函數f的正則性及解(13)的解析性．從式(14)中顯然可知

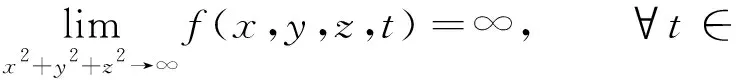
(16)

由此可得解(13)滿足

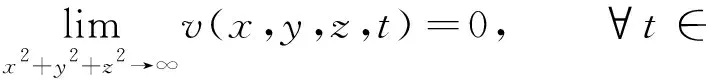
(17)

基于以上分析,解(13)在條件(12)、(15)、(16)和(17)下在空間各個方向都是有理局域的,因此被定義為lump解[11]．

為直觀地了解解(13)的性質,不失一般性,進一步考慮解(13)在y=0和t=0情形下的動力學特征．取參數α=γ=δ=a5=a6=1,β=-1,a1=a2=a7=a9=2,a3=5,a10=18,則解(13)簡化為

(18)

圖1(a)表明解(18)有3個極值點(一個波峰,兩個波谷且呈對稱形式),利用符號計算軟件MAPLE,我們發現波峰和波谷分別位于

(19)

和

(20)

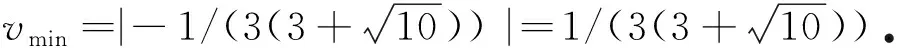
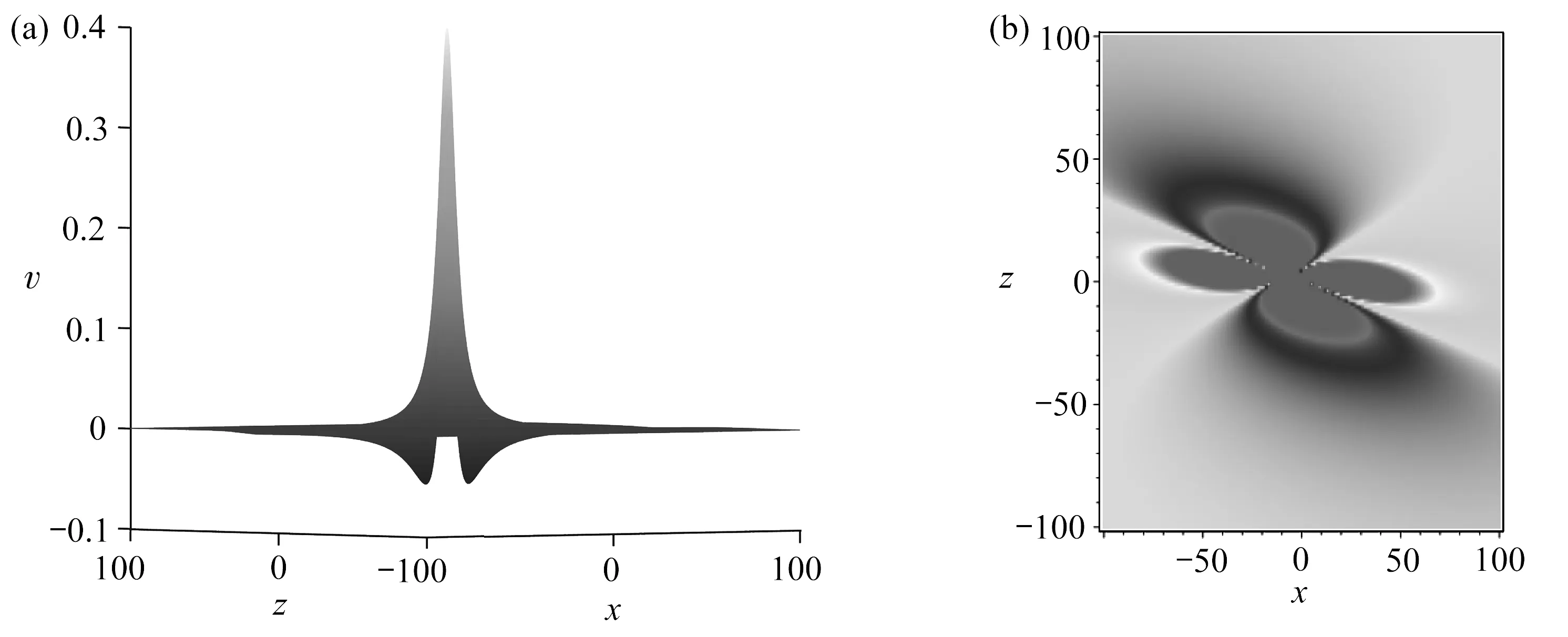
圖1 Lump解(18)的三維圖和密度圖(y=0, t=0)Fig. 1 The 3D plot and the density plot with lump solutions (18)(y=0, t=0)

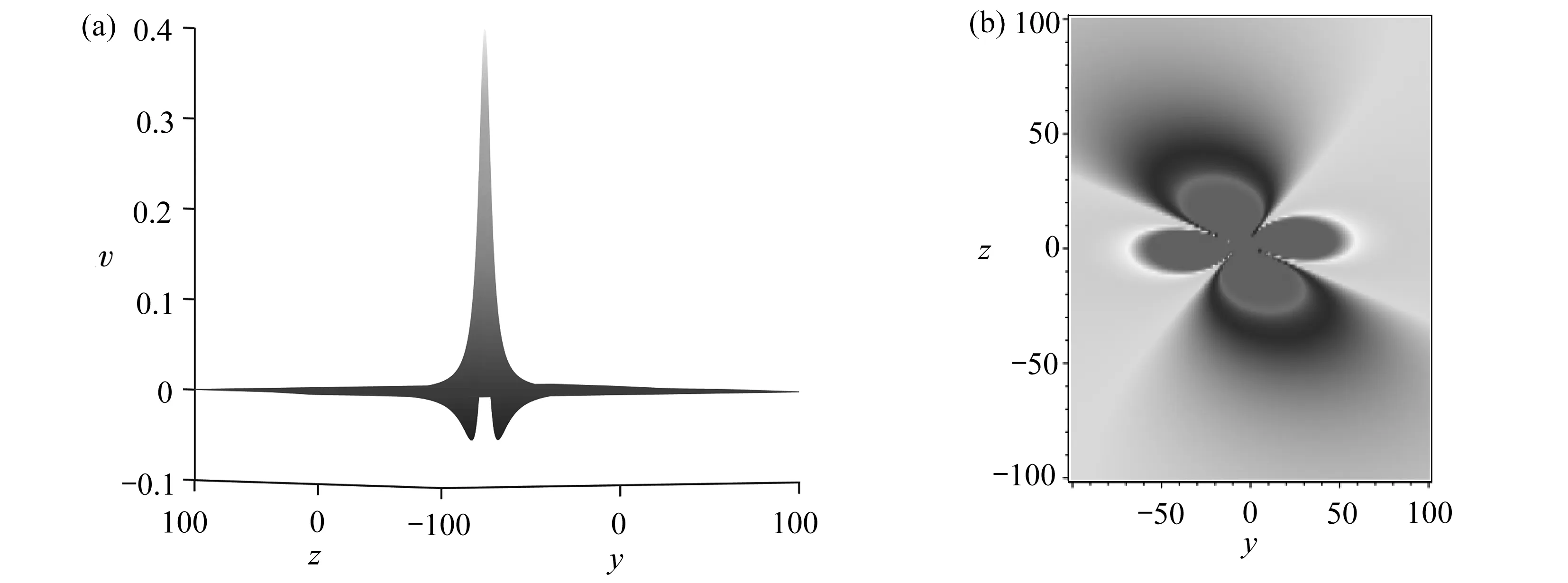
圖2 取參數α=γ=δ=a5=a6=1,β=-1,a1=a2=a7=a9=2,a3=5,a10=18時,lump解(13)的三維圖和密度圖(x=0, t=0)Fig. 2 The 3D plot and the density plot with lump solutions (13) under parameters selected as α=γ=δ=a5=a6=1, β=-1, a1=a2=a7=a9=2, a3=5, a10=18 (x=0, t=0)

1.2 Lump波與線孤子的相互作用解

本小節主要構造方程(1)的相互作用解．基于文獻[12-13],在式(9)中取l=0,可得

f=g2+h2+keη+a11,

(21)

其中g,h,η與式(10)相同．將擬設解(21)代入雙線性方程(8) 中,收集變量x,y,z,t和eη的不同冪次系數,求解相應的代數方程組,得到參數關系如下:

(22)

且需滿足如下條件:

(23)

由此,得到方程(1)的解為

(24)

其中

(25)

圖3展示了解(24)中lump波與線孤子相互作用過程中產生的“聚變”現象[42-43]．參數取值為β=-2,γ=-1,δ=a1=a5=a8=a10=k3=1,a3=5,a7=a11=0.5,k=2,k2=1/3,z=0．“聚變”現象的產生主要由解(24)中的多項式函數和指數函數引起．當k2>0,t→∞時,解(24)受指數函數影響較大,反之t→-∞時,解(24)受多項式函數影響較大．

(a) t=-5(b) t=-2(c) t=0

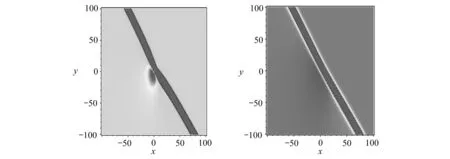
(d) t=2(e) t=6圖3 Lump波與線孤子產生的“聚變”現象Fig. 3 Fusion phenomena between the lump wave and the one-stripe soliton

如圖3(a)所示,當t=-5時,解(24)包含一個lump波和一個線孤子．隨著時間變化,lump波和線孤子逐漸靠近并漸趨融合．當t=6時,lump波完全融入線孤子中并最終消失,見圖3(e)．

當k2<0,圖4展示了lump波與線孤子相互作用中產生的“裂變”現象[42-43]．參數取值為β=-2,γ=-1,δ=a1=a5=a8=a10=k3=1,a3=5,a7=a11=0.5,k=2,k2=-1/3,z=0．從圖4中觀察可見,當t=-4時,解(24)只包含一個線孤子,隨著時間變化,一個lump波逐漸從線孤子中分離;當t=4時,lump波與線孤子完全分離,即產生所謂“裂變”,見圖4(e)．

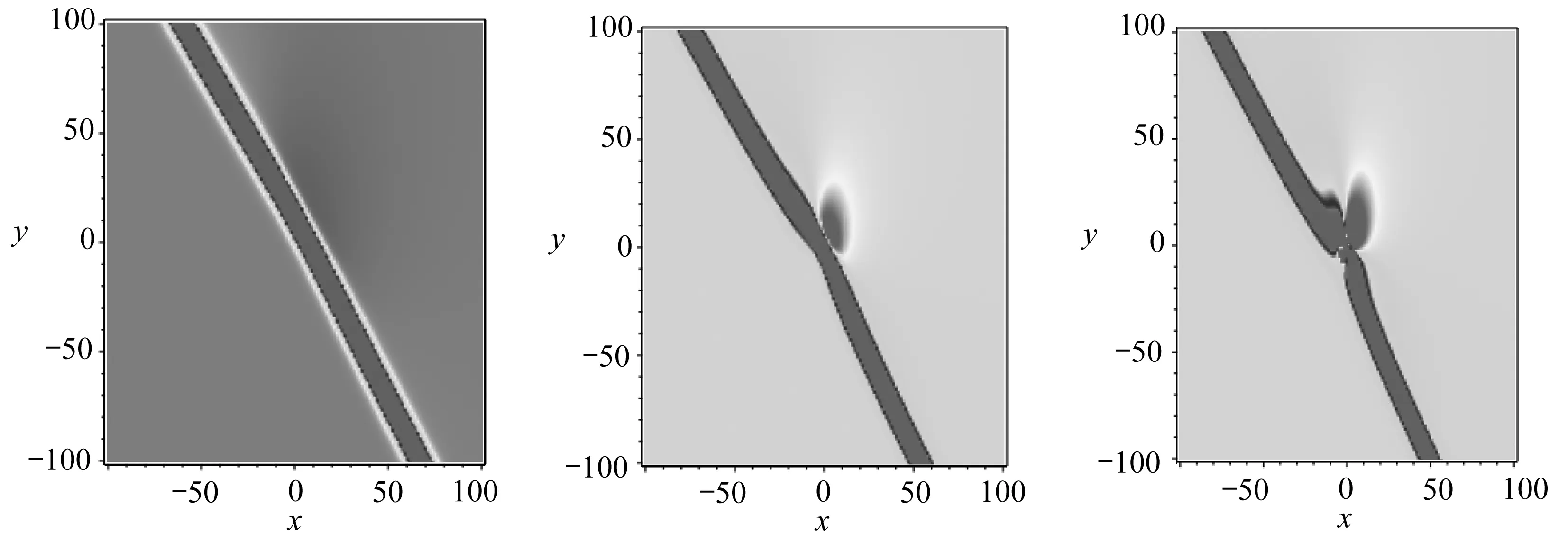
(a) t=-4(b) t=-1(c) t=0

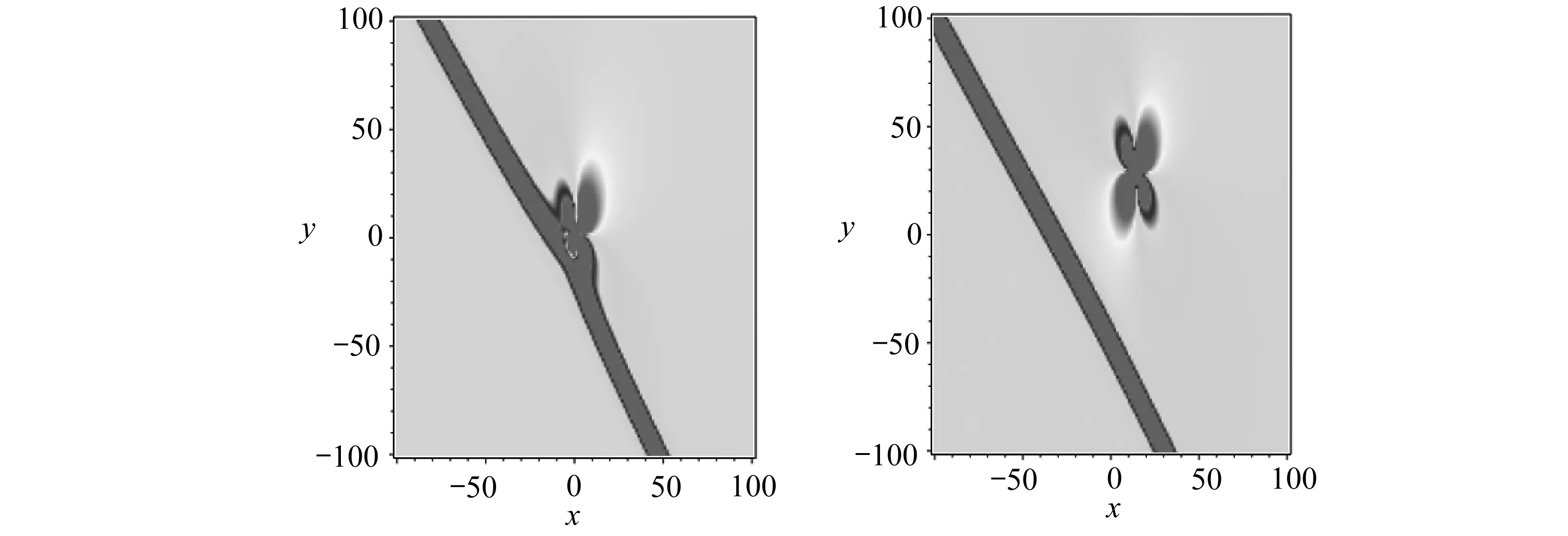
(d) t=0.5(e) t=4圖4 線孤子產生的“裂變”現象Fig. 4 Fission phenomena produced by the one-stripe soliton

1.3 呼吸子解

為構造方程(1)的呼吸子解,假設[44-47]

f=k1eξ1+k2cos(ξ2)+k3e-ξ1,

(26)

其中

ξ1=c1x+c2y+c3z+c4t,ξ2=c5x+c6y+c7z+c8t,

(27)

ci(i=1,2,…,8),ki(i=1,2,3)均為參數．類似于前面的計算,將表達式(26)和(27)代入雙線性方程(8)中,求解e±ξ1,cos(ξ1)和sin(ξ1)的不同冪次系數組成的代數方程組,可得

(28)

且需滿足如下約束:

αc2c5≠0．

(29)

由此,可得方程(1)的如下解:

(30)

其中

為便于理解呼吸子解(30)的特征,依次取z=0,y=0,x=0,圖5—7分別展示了呼吸子解在時間t=0時的動力學特性．

圖5 解(30)的三維圖(x-y-v),x曲線圖和密度圖,參數取值為α=γ=c5=c7=1, β=-2, c3=0, c2=k1=k3=3, k2=2Fig. 5 The 3D plot (x-y-v), the x-curve plot and the density plot of solution(30) with α=γ=c5=c7=1, β=-2, c3=0, c2=k1=k3=3, k2=2

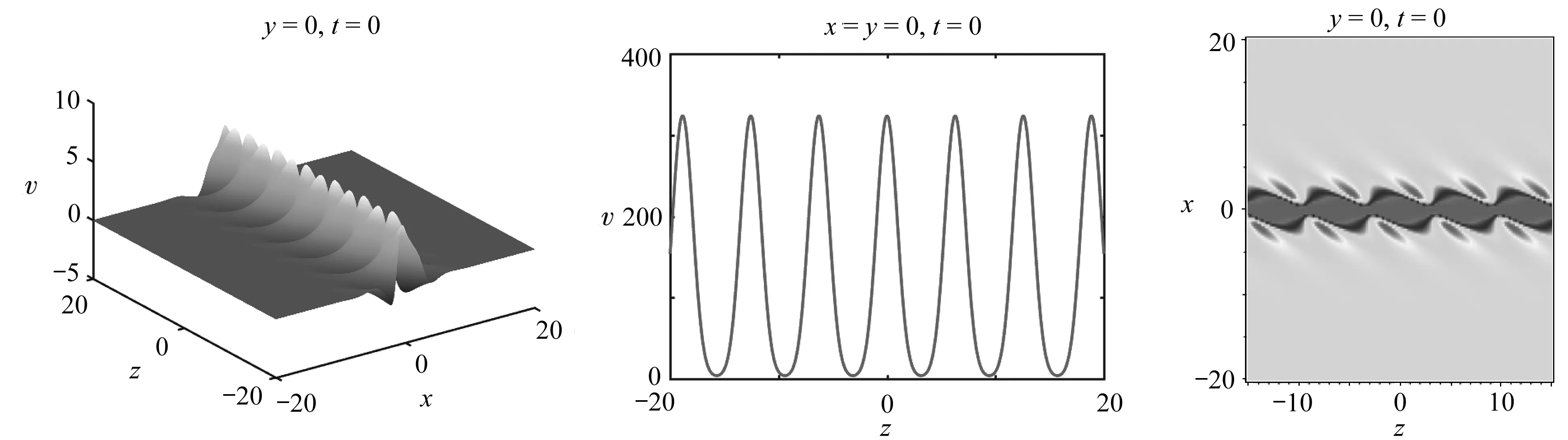
圖6 解(30)的三維圖(x-z-v), z曲線圖和密度圖,參數取值為α=γ=c2=c5=c7=1, β=-2, c3=0, k1=k2=k3=2Fig. 6 The 3D plot (x-z-v), the z-curve plot and the density plot of solution(30) with α=γ=c2=c5=c7=1, β=-2, c3=0, k1=k2=k3=2

2 結 論

本文主要研究了廣義(3+1)維KdV方程(1),得到了方程的lump解、相互作用解和呼吸子解．說明了lump解(13)的有理局域性,并通過圖1和圖2分別觀察到lump解在y=0和x=0時均存在3個極值點．基于相互作用解(24),圖3和圖4分別展示了lump波與線孤子相互作用過程中的“聚變”和“裂變”現象．當k2>0時,圖3展示了lump波與線孤子發生碰撞后的相互融合;當k2<0時,圖4展示了線孤子分裂為線孤子和lump波的過程．最后,圖6展示了解(30)的周期性傳播特征．