基于稀疏Bayes學習算法的無約束結構荷載重構方法

陳先智, 周新元, 曾耀祥, 張亞輝

(1. 大連理工大學 工業裝備結構分析國家重點實驗室, 遼寧 大連 116024;2. 北京宇航系統工程研究所, 北京 100076)

0 引 言

隨著航空航天技術的快速發展,對運載火箭的優化設計也提出了更高的要求,準確描述其自由運行過程中的外激勵,是結構優化設計的一個重要方面．火箭在運行過程中,外激勵通過傳感器直接測量往往比較困難,在此背景下,發展通過響應信息間接獲取外部激勵的荷載重構方法有著重要意義．

隨著荷載重構方法的發展,其不適定性引起了許多學者的關注,而正則化理論被廣泛應用于解決各種不適定性問題[1-3]．彭凡等[4]使用Green函數構建荷載和響應之間的關系,引入奇異值分解(SVD)改善矩陣病態,進而重構了自由結構的沖擊荷載．周玙等[5]綜合利用結構的位移模態和應變模態參數實現了應變到位移的轉換,避免了空間積分,反求出位移響應后,結合擴展Tikhonov正則化實現了基于應變響應的自由體荷載識別．Liu等[6]組合Tikhonov正則化和截斷廣義奇異值分解(TGSVD),綜合兩者的優點,成功識別了動力荷載．Qiao等[7]采用三次B樣條函數結合截斷奇異值分解法(TSVD),解決了沖擊荷載識別問題．張超東和黎劍安[8]利用Kalman濾波算法獲得了增秩狀態向量的最小方差無偏估計,實現了狀態和荷載向量的同時識別．

由于l2正則化存在過擬合的現象[9],因此近幾年有學者通過稀疏正則化改善這一現象．稀疏正則化所對應的問題為l0正則化,在數學上是難以求解的,一般凸釋放為l1正則化求解．Qiao等[10]使用字典建立識別方程,并采用可分離近似法(SpaRSA)重構荷載．由于字典質量對識別結果有影響,Zhang等[11]使用雙稀疏字典學習改善字典的質量,進而改善了識別結果．Liu和Li[12]使用盲源分離(BSS)算法結合正交基追蹤算法(OMP),等效識別了時空耦合的分布荷載．Samagassi等[13]使用縱向應變響應在低噪聲情況下結合小波相關矢量機(WRVM)稀疏重構了沖擊荷載．Yan和Sun[14]通過脈沖響應函數建立荷載與響應的關系,利用沖擊荷載的稀疏特性,使用非負Bayes學習算法識別了沖擊荷載．

針對大維度荷載重構問題時,其計算成本會變得非常大,因此一般常用的手段為分段擬合．對于線性時不變系統而言,結構響應由初始條件引起的自由振動和荷載引起的強迫振動線性疊加而成,而各分段的初始條件難以通過測量得到,因此分段擬合最重要的是如何合理表達未知初始條件．Prawin和Rama Mohan Rao[15]表達初始條件的連續遞推公式受噪聲影響較大,且有誤差累積和不適定現象．張開華[16]假設初始條件為上一段重構荷載作用下結構末狀態的響應,但是僅選取末狀態響應作為初始條件,會導致重構精度嚴重依賴上一步重構結果．考慮到對于一個多自由度系統而言,在外力作用時,通常只會激起一些較低的振型,大部分高階振型被激起的分量很小,一般可忽略不計．Pan等[17]用低階振型表示初始條件,使用快速軟閾值迭代算法(FIST)結合Bayes信息準則(BIC)成功識別了未知初始條件下的荷載,但是識別效率較低．在此基礎上,Pan等[18]采用矩陣正則化構建長時間荷載改善了識別效率,為進一步提高效率,利用各分段可以單獨重構的特點,使用并行算法同時重構所有分段荷載[19],但是忽略了各分段之間的聯系,不能充分利用上一段的重構結果．為了能高效處理含有未知初始條件與大維度荷載重構的問題,在現有文獻基礎上,本文提出利用線性系統的疊加原理,將荷載使用三角基函數擬合,分別求解了所有荷載基函數作用下的強迫振動響應和低階振型,作為初始位移、初始速度的自由振動響應,直接使用稀疏Bayes學習(SBL)算法的快速算法[20-21]對未知分解系數進行求解．提出了改進分段擬合的思想,將上一分段求解得到的荷載作用在結構上,產生的末狀態響應作為可能初始條件,并使用低階振型做補充,通過不斷更新的系數矩陣,高效完成了大維度荷載重構問題．

1 重構方程的建立

對于自由度為n的結構體而言,其運動微分方程為

(1)

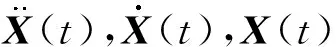
假設阻尼為比例阻尼,令X=Φu,將其代入式(1),并前乘ΦT,根據振型的正交性,假設模態截斷數為q,式(1)可解耦為

(2)

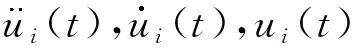
對于線性系統而言,含初始條件的結構響應可以分解為無初始條件強迫振動響應和有初始條件自由振動響應．因此可以先建立無初始條件的響應-荷載關系,由Duhamel積分可知,式(2)的模態加速度響應[22]為

(3)

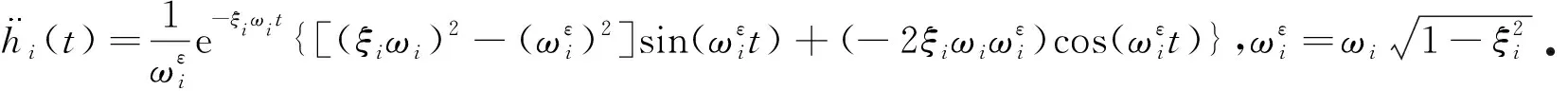
(4)

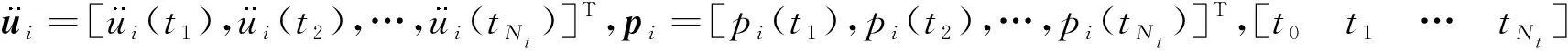
(5)

假設結構上作用有Nf個荷載,測點有Nm個．由于是線性系統,那么Nf個荷載作用下的結構響應可以分解為每個荷載單獨作用下的響應之和．令fk為第k個荷載(k=1,2,…,Nf)作用在自由度lk的荷載,則其相應的模態荷載pik可表示為

pik=φilkfk,

(6)

式中φilk表示第i階模態中自由度為lk處的值,fk=[fk(t1)fk(t2) …fk(tNt)]T．

將式(6)代入式(4)得到第i階模態加速度為

(7)

式中Hilk=φilkhi．當不考慮噪聲影響的情況下, 由振型分解法可得當fk單獨作用時, 第j個測點的加速度響應為

(8)

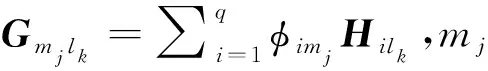
在荷載重構領域中,由于通過函數擬合可以改善求解時矩陣的性態,故一般將荷載函數通過一系列的正交基函數近似展開,因此fk(t)可表達為

(9)

(10)

式中odd表示奇數,even表示偶數,Δω表示頻率間隔,nb和Δω可根據響應的頻譜和所關心頻率綜合估算．對式(9)在時域離散,并代入式(8),得

(11)

稱ajk=GmjlkBk為元胞,表示當全體荷載基函數分別作用在加載點k時,測點j響應的集合,式中yk=[y1ky2k…ynbk]T,

(12)

根據疊加原理,測點響應與未知系數的關系為

(13)

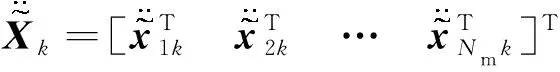
(14)

測量響應一般含有噪聲,因此式(13)可以改寫為

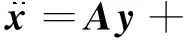
(15)

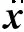
至此建立了已知測點響應和未知系數之間的關系．由于未知噪聲的存在,直接通過對系數矩陣A求逆,解未知系數y,往往會導致較大的誤差,因此本文使用SBL算法求解未知系數y,并用式(9)對荷載進行重構．

2 稀疏Bayes學習算法推導

在Bayes模型中,誤差被概率性的建模為零均值Gauss分布,方差為σ2[20]．本文假設噪聲項服從N(0,σ2I),I表示單位陣,方差σ2從數據中估計得出,則的似然函數為

(16)

式中N=Nt×Nm．

為了得到稀疏解,假設存在超參γi,y中元素yi的均值為0,方差為1/γi．那么y的先驗表示為

(17)

式中M=Nf×nb,γ=diag(γ1,γ2,…,γM)．

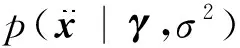
(18)

由Bayes公式,可以得到y的后驗:

(19)

式中

Σy=(σ-2ATA+γ)-1,

(20)

(21)

其中Σy和μy分別表示y的方差和均值．計算出y的均值μy后,此時μy即為所求基底系數,結合式(9)即可重構荷載．為快速確定未知的參數σ2和超參γ,使用文獻[21]中的快速算法．

3 未知初始條件的處理

采用較小的時間間隔能提高荷載重構的精度,但這也會導致更大的預處理成本．為了提高預處理的效率往往會將測量響應分成多個沿時間軸移動的分段,荷載按順序在每個分段單元重構,分段示意圖如圖1所示．

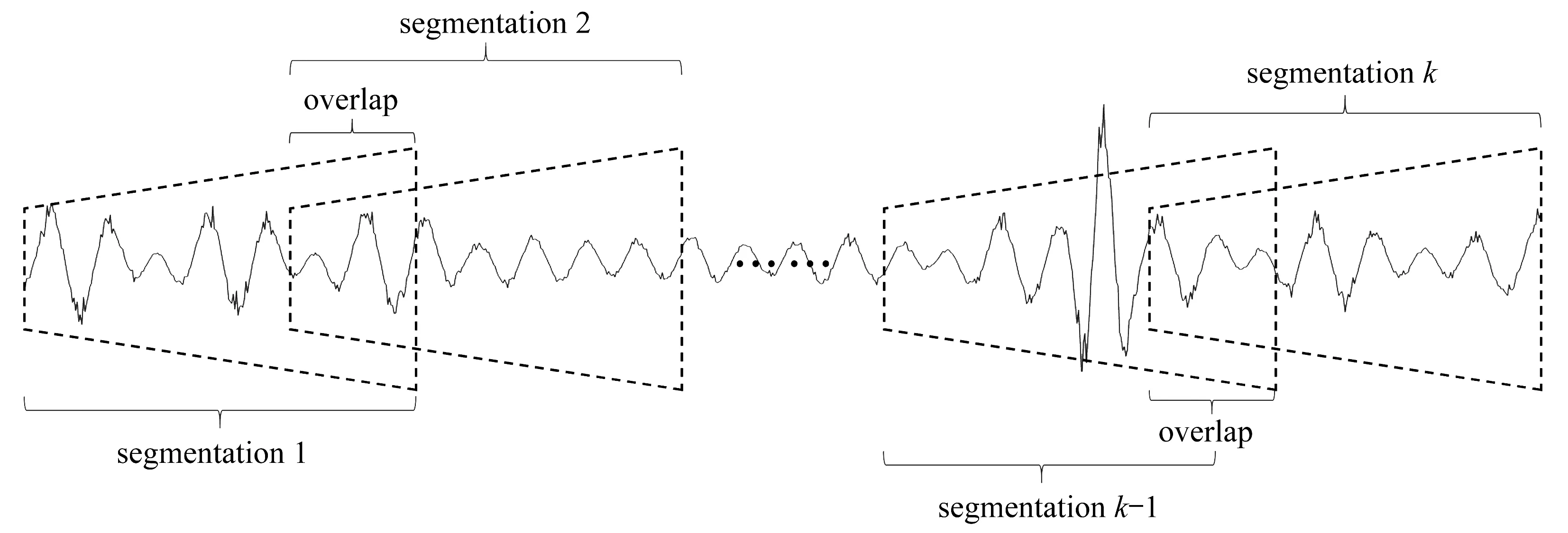
圖1 分段重疊擬合Fig. 1 Piecewise overlap fitting

為合理表達每個分段的初始條件,本文結合SBL算法的稀疏特性,提出改進分段擬合思想,其選用末狀態響應作為可能初始條件,由于可能的初始條件與真實的初始條件有差異,因此引入低階振型作為初始條件的補充．

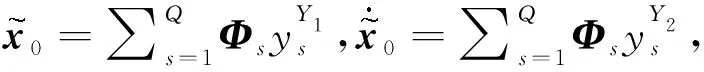
(22)

式中djs表示初始位移向量僅為Φs時,引起的第j個測點自由振動的加速度響應;vjs表示初始速度向量僅為Φs時,引起的第j個測點自由振動的加速度響應;Q為選取參與組合初始條件模態的數量,本文選取前50階彈性模態．

將初始條件使用上一分段的末狀態響應和補充初始條件表示,則第j個測點的加速度響應可以近似表示為

(23)

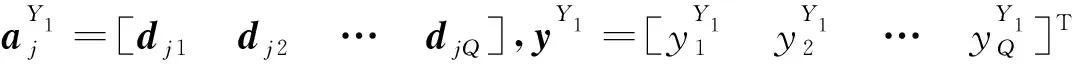
(24)

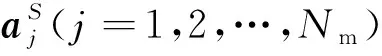
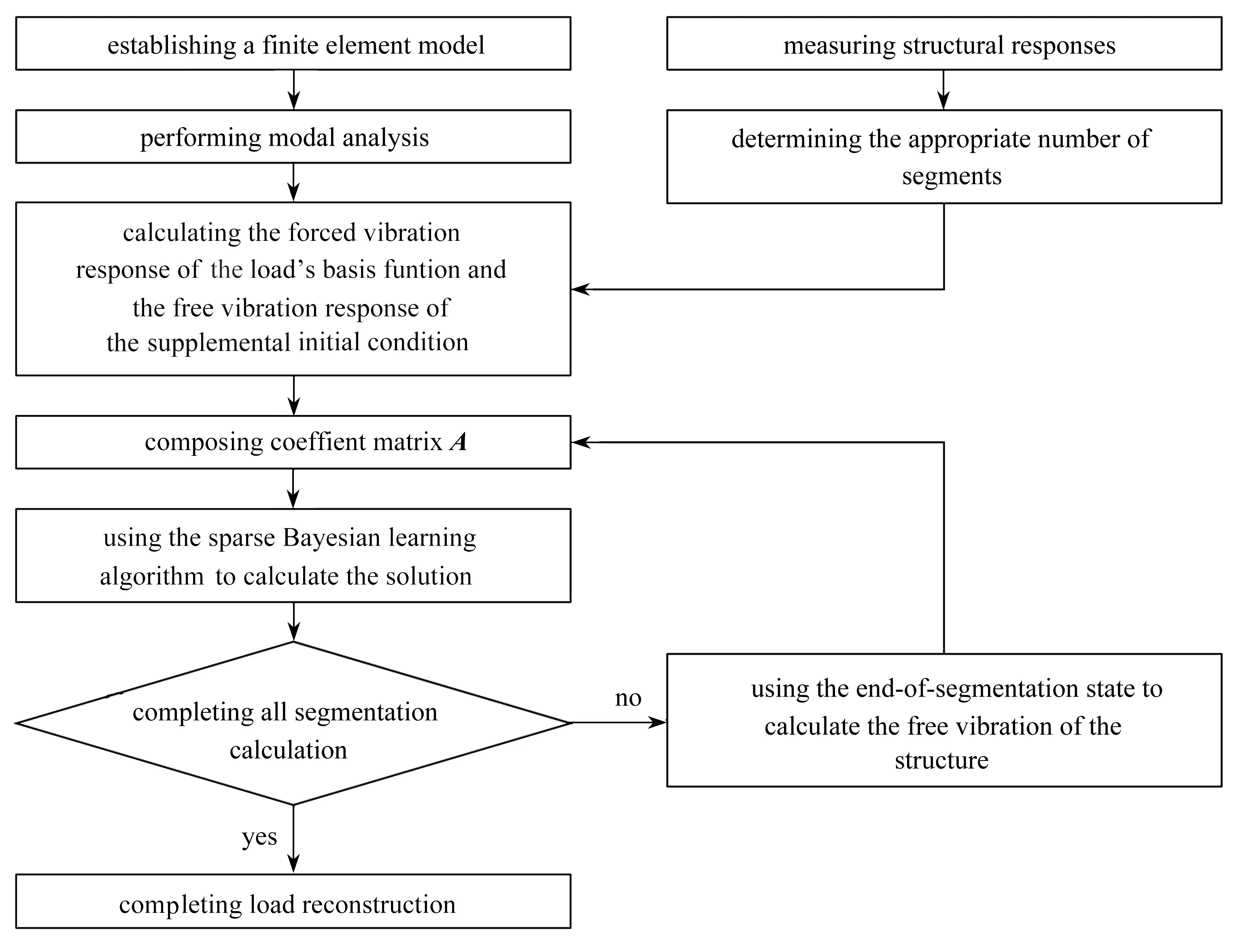
圖2 所提方法荷載重構流程圖Fig. 2 The flowchart of the proposed method for load reconstruction

4 無約束結構的處理

火箭在自由飛行的過程中是一種無約束結構,這種結構存在剛體運動,而傳感器測量的響應為結構的彈性響應,因此需要剔除結構運動中的剛體運動成分．于是將結構響應分解為剛體響應和彈性響應:

(25a)

(25b)

(25c)

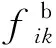
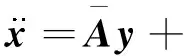
(26)

式中

(27)

5 數值算例驗證

本文采用文獻[23]中的模擬無約束火箭模型,模型的直徑為3 m,壁厚為0.005 m,長50 m,101個節點分成100個單元,相鄰節點間隔為0.5 m,彈性模量E=7×1010N/m2,剪切模量G=2.65×1010N/m2,各節點加集中質量1 600 kg,繞縱軸的轉動慣量為100 kg·m2,繞橫軸的轉動慣量為50 kg·m2,基頻為1.05 Hz,阻尼比為0.01,采樣頻率為1 000 Hz．響應計算使用前50階彈性模態．本文選取401個基函數,采用等間隔頻率Δω=0.25 Hz．

采用整體相對誤差(R)定量地衡量荷載重構精度,其表達式如下:

(28)

式中,Rj表示第j個重構荷載的整體相對誤差,fTj表示第j個真實荷載向量,fIj表示重構的第j個荷載向量,‖·‖1表示向量的1-范數．

為了模擬真實情況,對加速度響應數據施加Gauss白噪聲,公式如下所示:

(29)

5.1 所提方法有效性驗證

為了驗證本文所提方法的有效性, 假設有3個荷載作用在結構上, 荷載作用在距離頂端0.5 m,1.5 m,2.5 m處,荷載作用方向為橫向,荷載的時間歷程函數為

(30)

模型的初始位移和初始速度如圖3、圖4所示．

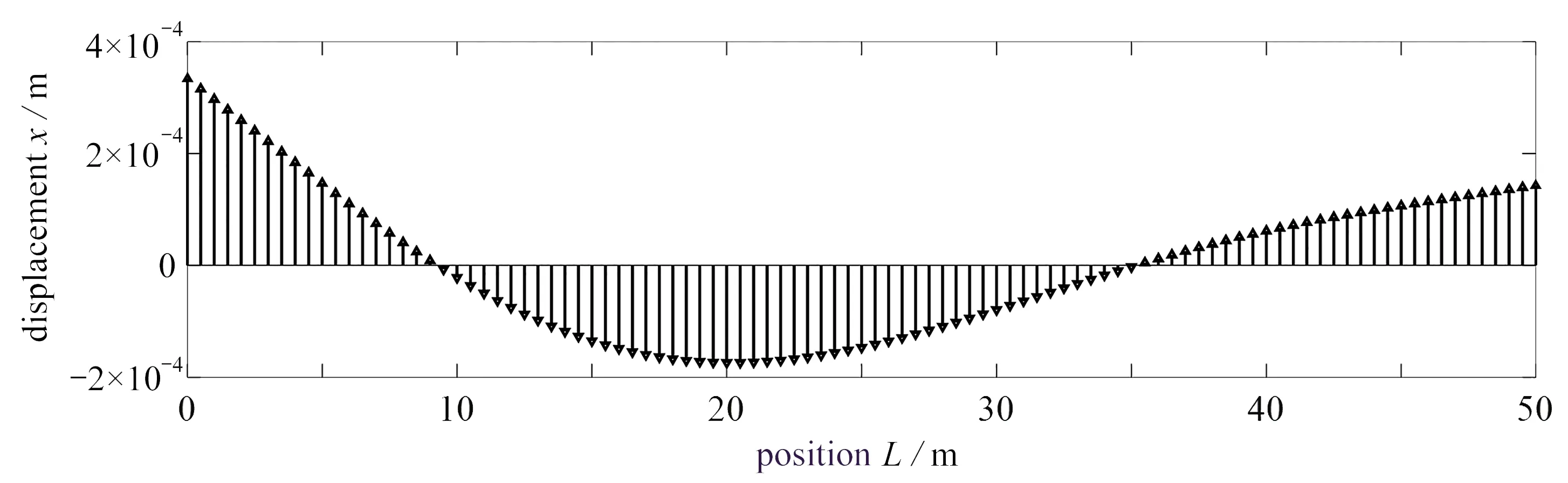
圖3 初始位移Fig. 3 Initial displacements

6個加速度傳感器安裝在距離頂端1 m,2 m,3 m,4 m,5 m,5.5 m處,使用5%,10%和15%三個噪聲等級驗證方法的抗噪性．

在不同噪聲等級下,使用本文所提的方法三點加載荷載重構結果如圖5所示．由圖中可以看出,本文所提方法重構的荷載都基本和原荷載重合,驗證了本文方法對于不同噪聲水平的魯棒性和可行性．

為了說明所提方法的優勢,將本文所提方法與文獻[24]中加權l1正則化方法(weightedl1-norm regularization method)在計算精度和效率上進行比較．由于兩種方法采用相同的基函數,所以預處理即計算荷載基函數結構響應的時間成本相同,因此在兩種方法的計算成本對比上,僅列出計算式(26)所需的時間．

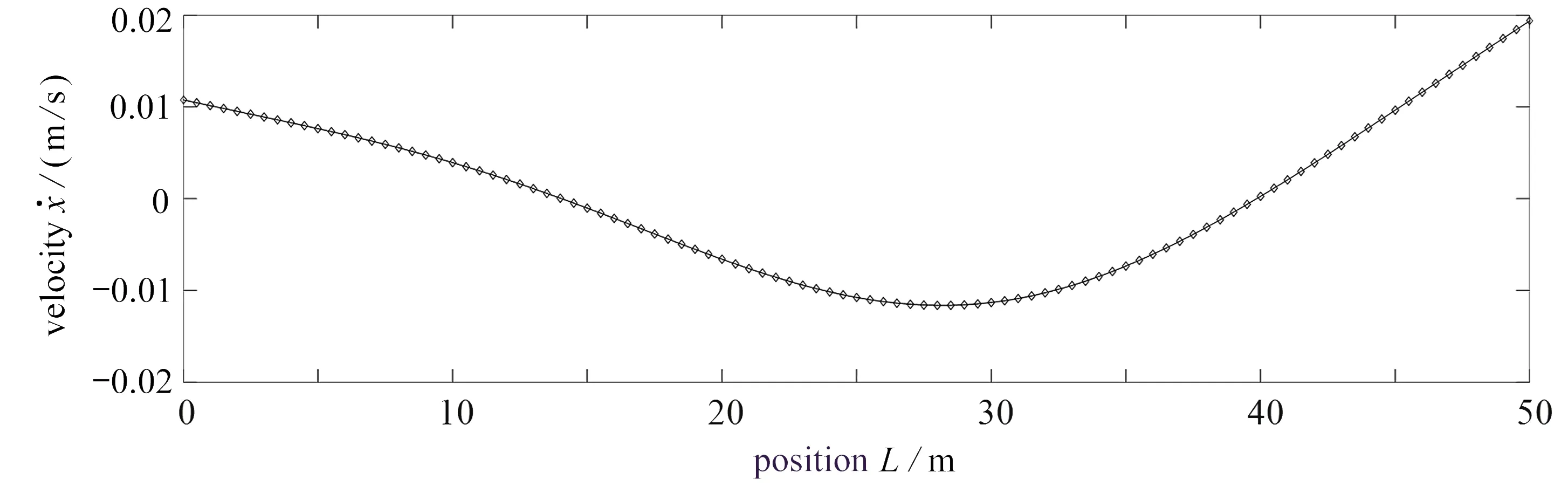
圖4 初始速度Fig. 4 Initial velocities

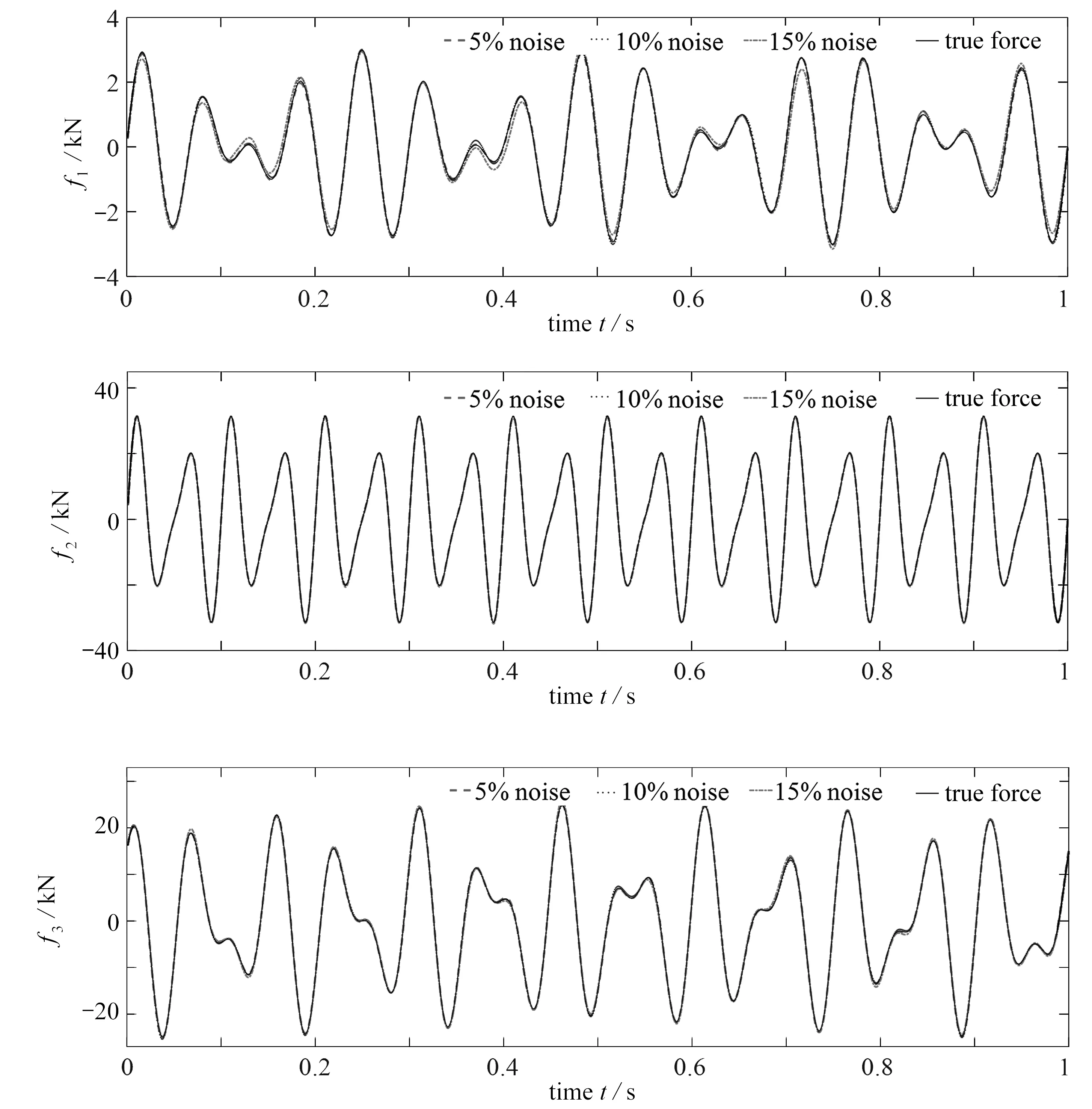
圖5 本文所提方法不同噪聲水平下荷載重構結果Fig. 5 Reconstruction results with the proposed method under different noise levels

由表1可知,本文所提方法與加權l1正則化方法在重構精度上相差無幾,但是計算的平均時長僅為0.68 s,而加權l1正則化方法的平均時間則需要617.02 s．以15%的噪聲為例,荷載重構的結果如圖6所示,從圖中可以看出,本文所提方法和加權l1正則化方法均能比較準確地重構出真實荷載,僅在幅值處有略微的差別．

由上可以得出,本文所提方法和加權l1正則化方法都能夠處理未知初始條件下的荷載重構問題,且在幾乎相同求解精度的情況下,本文所提方法通常能夠更快地獲取重構結果．

5.2 改進分段擬合驗證

為驗證本文選取初始條件表達方式的合理性,式(24)中的初始條件項僅由低階振型表達[18]和本文所提改進分段擬合做比較．至于僅考慮將上一分段末狀態作為初始條件的情況[16],由于受上一步計算結果影響,結合本文方法后,重構效果非常不理想,因此本文便不再與其進行比較．

假設荷載加載點距離頂端0 m,2 m,4 m,加速度傳感器距離頂端0.5 m,1.5 m,2.5 m,3.5 m,4.5 m和5.5 m,加速度響應數據施加15%的噪聲,測量的加速度響應時間為4 s．對響應曲線進行分段,本文所提改進分段擬合思想重疊長度為0,每段時間長為2 s．根據測點和加載點位置調用相應的元胞,組成系數矩陣．荷載函數表達式為

(31)

僅使用低階振型表達初始條件的重構結果和本文所提改進分段擬合的重構結果如圖7、圖8所示．為了清楚對比兩種不同初始條件表達的荷載重構效果,將圖7中重構荷載f2第2秒的銜接點放大,如圖9(a)所示,同樣將圖8中荷載f2第2秒的銜接點放大,如圖9(b)所示,并結合表2可以明顯看出,僅使用低階振型表達初始條件的重構結果并不理想,而本文所提改進分段擬合的重構結果基本與真實荷載重合,并且兩者在計算效率上也幾乎相同．由此可以得出,本文所提改進的分段擬合是合理、有效的．

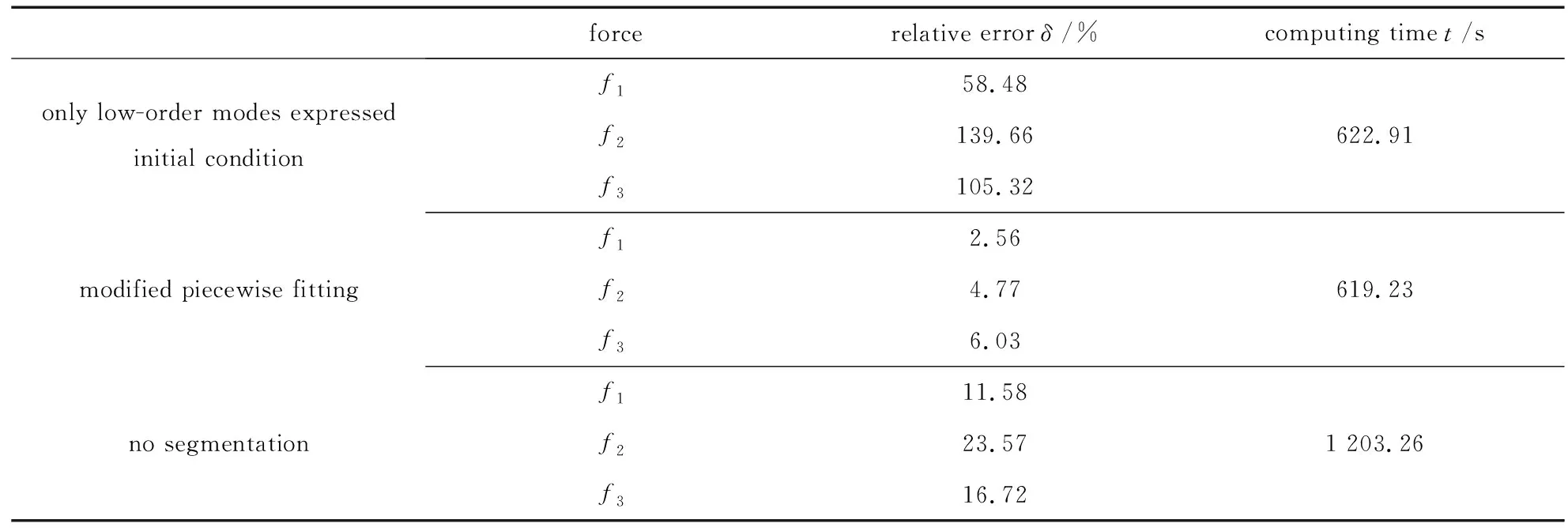
表2 3種重構方式識別結果對比

對比不分段和分段的整體相對誤差,分段之后精度比不分段的精度略好,這是因為選擇了合適的分段長度并且荷載比較復雜．采用分段擬合重構荷載所需時間約占不分段重構荷載的1/2,這是由于不分段意味著預處理所需計算響應的時間維度更大,相應的時間成本也更大．由此,本文所提的改進分段擬合方法,在采用合適分段長度的情況下,能夠高效準確重構大維度的復雜荷載．

由上可知,本文提出分段擬合的思想能明顯提升計算效率,對于復雜的荷載分段擬合也能夠提高反演精度．針對大維度荷載重構問題,本文認為分段長度不宜太長,太長會導致預處理的成本過大,當荷載比較復雜時還會導致重構精度降低．

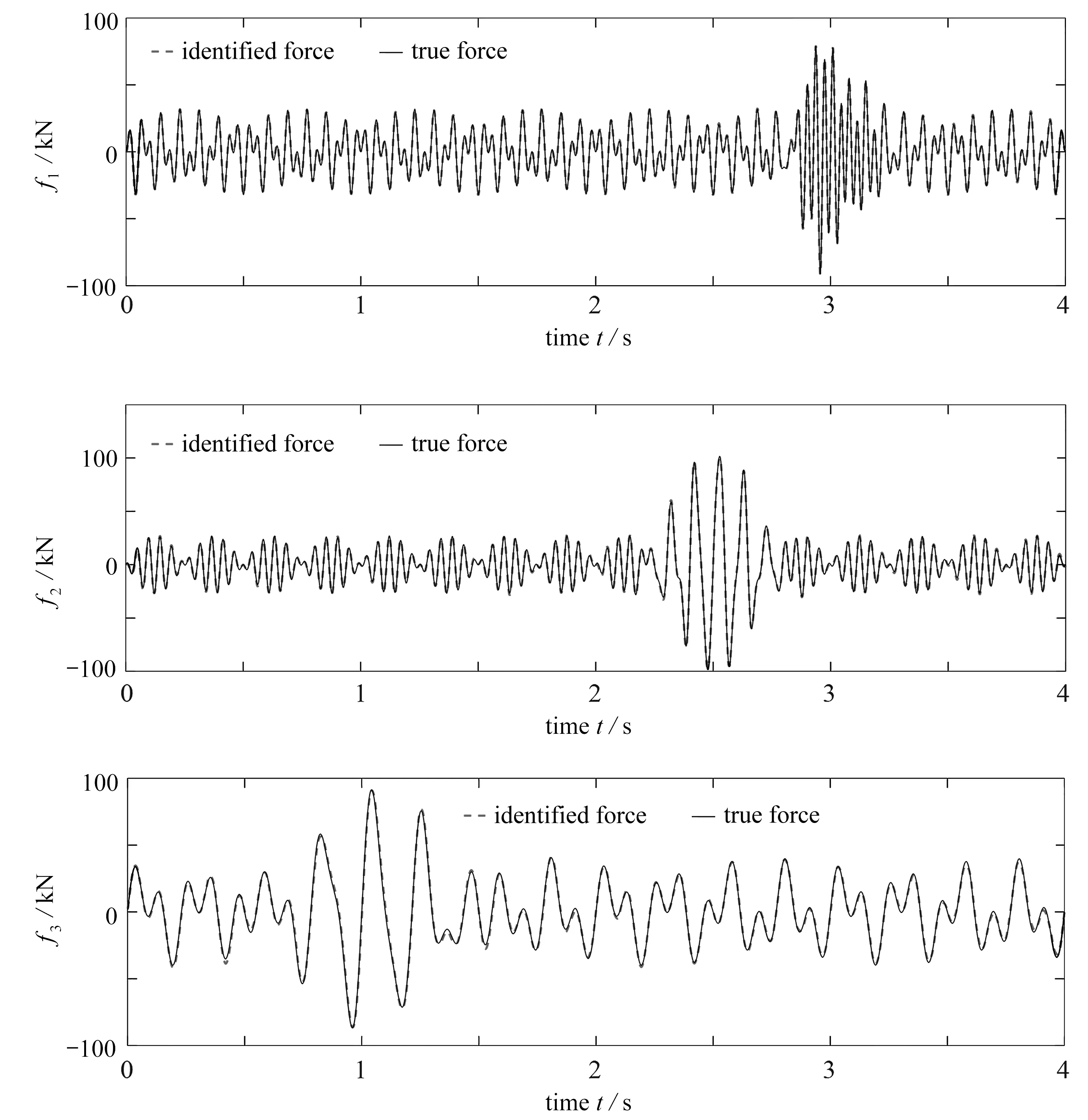
圖8 改進分段擬合Fig. 8 Modified piecewise fitting time histories

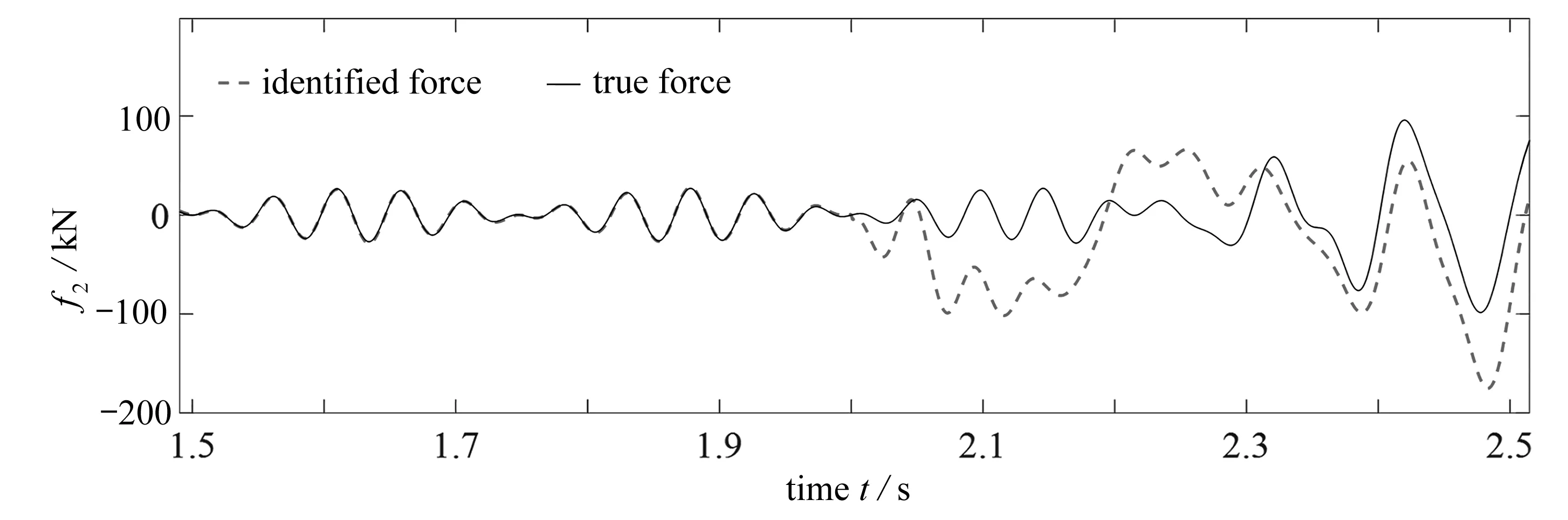
(a) 僅使用低階振型表達初始條件(a) Only low-order modes expressed initial conditions

(b) 改進分段擬合(b) Modified piecewise fitting time histories圖9 銜接點放大圖Fig. 9 The articulation point enlargement

6 結 論

本文針對含有未知初始條件無約束結構的荷載重構問題,提出基于SBL算法荷載識別方法結合改進分段擬合提高了整體的計算效率,并在識別過程中利用了上一分段的識別結果,通過合理的初始條件表達方式,改善了識別的精度．數值結果也表明,本文方法較現在流行方法能夠更快速地重構荷載,且通過不同等級噪聲下的重構結果,驗證了本文方法具有較強的魯棒性;和僅使用低階振型表達初始條件相比,采用的改進分段擬合更加合理;改進的分段擬合手段在采用合適的分段長度的情況下,和不分段的識別結果相比,也能夠以較高的精度重構荷載．