基于GA-PS的三維空間源項反演算法
陳松, 朱東升, 左欽文, 韓朝帥
(軍事科學院 防化研究院, 北京 102205)
0 引言
由于大國之間博弈以及中小國家間的利益沖突所導致的傳統核生化威脅依然存在且持續顯現。同時,以次生核生化危害、核生化恐怖活動和工業核生化事故為主要代表的非傳統核生化威脅,正日益加劇[1-3]。自從“9.11”事件后,全球各地恐怖襲擊頻現,給各國人民的生命安全帶來了嚴峻挑戰。2013年8月敘利亞大馬士革東部郊區發生化學武器攻擊事件,含有致命毒氣的化學武器造成了300名以上平民的死亡。2015年8月12日,位于天津市濱海新區的瑞海公司危險品倉庫發生火災爆炸事故,事故爆炸總能量約為450噸TNT當量,造成重大人員傷亡和財產損失。2020年8月4日,黎巴嫩首都貝魯特港口區發生巨大爆炸,爆炸接連發生兩次,導致多棟房屋受損,玻璃被震碎,天上升起紅色煙霧。造成至少190人死亡、6 500 多人受傷,3人失蹤。化學危害事故發生后,如何能夠快速確定危害源位置和源強,快速預測一定時間后的擴散濃度分布情況,對于輔助制定人員救治、防護、撤離方案,最大限度減少人員傷亡和財產損失有著重要意義。
近年來,通過在無人機上搭載化學傳感器實施三維空間探測已經成為趨勢,但通過三維空間探測數據進行源項反演的研究還很少。大量學者對化學危害事件的源項反演方面做了研究,包括使用差分進化算法[4]、神經網絡算法[5-6]、粒子群優化算法[7]、卡爾曼濾波算法[8]、參數敏感性分析方法[9]以及遺傳-單純形耦合算法[10]等,Wang等[11]對多點源污染事件提出兩步反演算法,但以上研究大都停留在了二維層面,或將危害源設置在地面或忽略危害源高度,或將監測點設置在地面,均未考慮三維空間情形。史陽[12]利用單純形搜索算法對源高進行了反算,但在理論數據條件下,誤差仍超過40%。陳增強[13]將模式搜索算法引入到源項反演中,然而僅對源強度一維參數進行了反算,后續研究中,其又完成了地面源項的反演[14],但仍未拓展到三維空間中。胡峰等[15]基于1958年美國草原SO2泄漏實驗數據[16],使用人群搜索算法(SOA)[17]開展了三維條件下反演性能評估,但由于SOA是啟發式算法,結果具有隨機性,單一使用SOA反演結果誤差較大。
在以往算法中,對此類問題求解相對困難,例如基于貝葉斯的反算方法,通過先驗概率和似然函數求解后驗概率,需要先知道先驗概率才能求解,假設先驗概率已知,每多加一個維度,目標函數均需要重新計算,維度較高時,可能存在無法求解的情況。
通過深入研究遺傳算法和模式搜索算法在多參數條件下的反演機制,建立了一種混合優化方法,充分利用了遺傳算法的全局尋優性能和模式搜索算法的局部尋優性能,探索了對源強及源三維空間位置的反算能力。在理論計算數據基礎上,利用三維空間中隨機分布點濃度,能夠實現對源空間位置和源強的高精度反算,通過仿真數據和SF6實測數據驗證了該算法的可行性。結果表明,該算法能夠快速準確地利用三維空間探測數據反算出源項的三維空間最優解。
通過對源項的有效定位,為化學危害事件后續的擴散預測和危害區域精準防護提供了先決條件。
1 算法在三維空間中的設計與實現
1.1 遺傳算法在三維空間中設計與實現
遺傳算法是模擬大自然中生物進化原理,將自然選擇和遺傳學機理通過數學方式進行表達,通過對各參數段在定義域上進行合理劃定,將各參數進行編碼、匹配成統一的類似生物基因組一樣的基因結構序列,利用選擇、交叉、變異等操作在解空間中搜尋最優解,通過合理設計基因序列和選擇、交叉、變異算法,能夠實現對全域范圍的搜索,較快地獲得較好的優化結果。遺傳算法已廣泛地應用于組合優化、機器學習、信號處理、自適應控制和人工生命等領域[18]。
遺傳算法流程如圖1[19]所示。
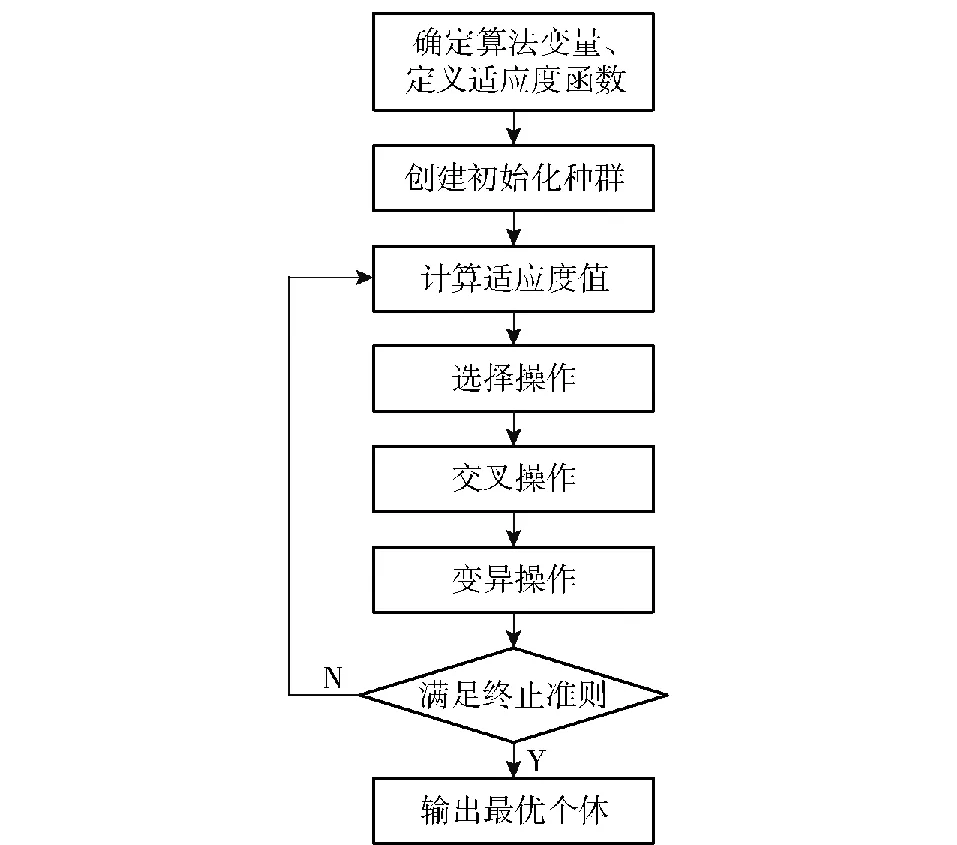
圖1 遺傳算法流程圖[19]
遺傳算法在三維空間中求解的實現:
1)初始化變量。包括種群規模N、交叉概率CR、變異概率MR,確定適應度函數f(s),即觀測數據與計算數據的差值平方和。
2)初始化種群。隨機創建N個向量[x,y,He,Q],x、y為危害源坐標,He為危害源有效高度,Q為源強,由這N個向量構成一個N行的數組,也即N個基因結構序列。其中x、y、He、Q均在其定義域隨機選定,x∈[0,max_x],y∈[-max_y,max_y],He∈[0,max_He],Q∈[0,max_Q]。
采用實數編碼,種群初始化如下:
pop.individual=rand(N,4);%pop.individual=(x,y,He,Q)
pop.individual(:,1)=pop.individual(:,1)*max_x;%(0,max_x)
pop.individual(:,2)=pop.individual(:,2)*max_y-rand( )*max_y;%(-max_y, max_y)
pop.individual(:,3)=pop.individual(:,3)*max_He;%(0, max_He)
pop.individual(:,4)=pop.individual(:,4)*max_Q;%(0, max_Q)
式中:rand( )函數產生由(0,1)之間均勻分布的 1個隨機數,rand(N,4)產生由(0,1)之間均勻分布的N行4列個隨機數。
3)計算適應度。將N個s=[x,y,He,Q]分別代入f(s),得到各自的適應度值f1,…,fN,值越小表明適應度越高。記錄最優個體s=[x,y,He,Q]。
4)選擇操作。計算每個個體的生存概率p=(sum(f1,…,fN)-fi)/sum(f1,…,fN)。
利用累計概率或輪盤賭的方式進行選擇操作。
以7個個體為例使用輪盤賭,如圖2所示。有7個個體組成的種群,每個個體的生存概率如圖2所示(f1的概率為θ/360°=59.84°/360°=16.6%,其他類推),利用隨機函數rand( ),依次生成[0,1]內的7個隨機數r,落在哪個區域,則哪個fi值對應[x,y,z,Q]保留,未落入的區域則被淘汰。適應度函數所對應的生存概率越大,被選擇保留的概率越大,相反,越不理想的值,生存概率越小,淘汰概率越大,即生物進化中的適者生存。
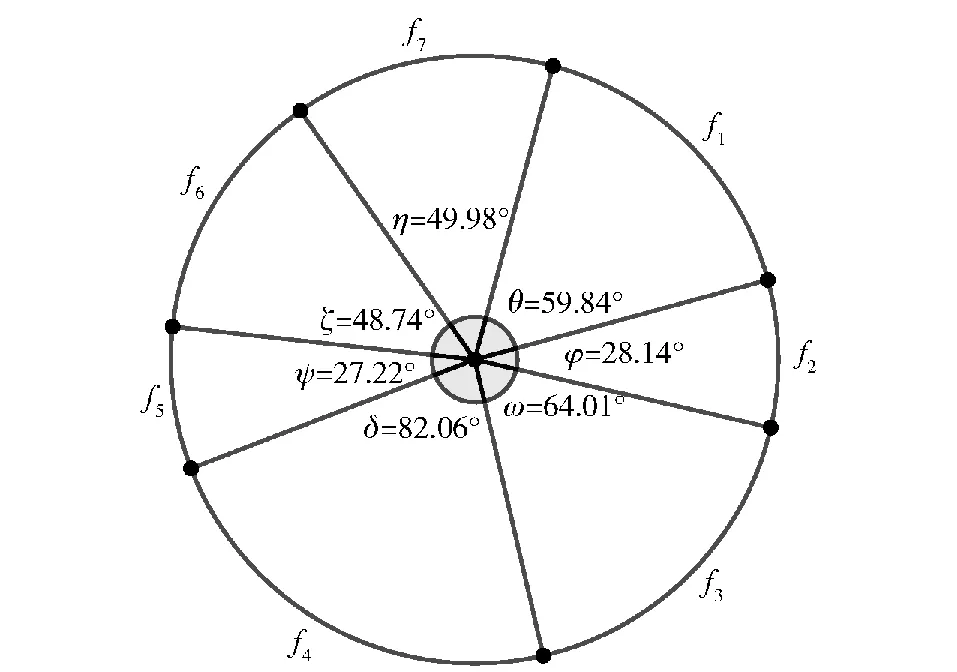
圖2 輪盤賭
由選擇操作,生成了新的種群,N個[x,y,He,Q]的數組,適應度低的個體被淘汰,適應度高的個體被選中,選中后的個體進行基因復制替換掉被淘汰的個體。
5)交叉操作。將N個[x,y,He,Q]的數組看成N個行向量,可以隨機選取任意兩個進行交叉操作,也可將N個行向量從第1行到第N行,進行兩兩配對(假設N為偶數,N為奇數時,最后落單的不處理)。
假設A是第1行個體,B是第2行個體。
隨機生成一個[0,1]的隨機數r=rand( )。如果r小于交叉概率CR,則將A和B進行交叉操作,如果r大于交叉概率CR,A和B不進行交叉操作,繼續對后續三、四行進行同樣判斷。
交叉操作實現:指定隨機交叉點,生成[0,1]內的隨機數p=rand( )。假設交叉后新個體分別為A1、B1。則A1=pA+(1-p)B,B1=pB+(1-p)A。
6)變異操作。對步驟5生成的新的N個[x,y,He,Q]個體,依次執行以下操作。
隨機生成一個[0,1]的隨機數r=rand( )。如果r小于變異概率MR,則將個體[x,y,He,Q]進行變異操作,如果r大于變異概率MR,則不進行變異操作。
變異操作實現:
隨機生成一個數n∈{1,2,3,4},n取1~4中一個數,假設n=3,則對He進行變異,相當于變異位置在He。
生成一個標準正太分布隨機數q=randn( )。假設He的取值范圍為[0,max_He],則變異后的He=He+q·max_He。為防止變異后,He值超出取值范圍,約定He<0時,He取0,He>max_He時,He取max_He。
7)終止條件判斷。完成變異操作后,生成新的種群N個[x,y,He,Q]。此為一輪遺傳算法,將新生成種群,作為輸入,重復執行以上操作步驟,直到到達指定的循環次數K,循環結束。最終生成的N個[x,y,He,Q]即為最后的種群,其中適應度值fi最小的D=[x,y,He,Q]的即為所求最優個體,D即遺傳算法的輸出值,也是輸入給模式搜索算法的初始值。
1.2 模式搜索算法在三維空間中設計與實現
模式搜索法[20]是一種直接搜索優化方法,該方法通過直接計算目標函數值來調整優化,而不需要求解梯度信息。該方法主要包括兩個步驟,即軸向探測和模式移動,首先通過軸向探測尋找到目標函數的下降的有利方向,進而利用模式移動沿著有利方向加速搜索。
算法從初始基點開始,交替實施兩種搜索:軸向搜索和模式搜索。軸向搜索依次沿n個坐標軸的方向進行,用來確定新的基點和有利函數值下降的方向。模式搜索則沿著相鄰兩個基點的連線方向進行,試圖使函數值下降更快。
模式搜索算法流程如圖3所示。

圖3 模式搜索算法源強反算流程
模式搜索算法在三維空間中求解的實現:
1)初始化變量,給定初始點X=[x,y,He,Q],令下一探測點Y=X,初始化加速因子α、收縮因子β、步長d=[d1,d2,d3,d4]、算法精度ε,適應度函數f(X),軸向探測循環控制變量j=1,模式探測循環控制變量k=1。構造探測向量e,即
2)如果f(Y+djej) 3)如果f(Y-djej) 4)根據源項實際,高度He和源強Q不得小于0,因此,如果Y(3)<0,令Y(3)=0,即He=0,如果Y(4)<0,令Y(4)=0,即Q=0。 5)如果j<4,則置j=j+1,轉步驟2,否則,進行步驟6。 6)如果f(Y) 7)置Temp=Y,令Y=Y+α(Y-X),X=Temp,置k=k+1,j=1,轉步驟2。 8)令Y=X,d=βd,置k=k+1,j=1。 9)為防止加速因子過大時,導致步長減小過快,無法繼續搜索,當α>1時,需判斷:如果d<ε,f(Y)值仍較大時,應恢復初始步長,置d=[d1,d2,d3,d4]。 10)如果d≤ε或k>1×105,則停止迭代,得到點X并輸出,否則,轉步驟2。 遺傳算法是一種優異的全局搜索算法,通過對求解參數進行基因編碼,實現在全域解空間中進行搜索,通過種群數量設置,能夠實現并行搜索能力。但由于搜索的隨機性,每次得到的解也是隨機變化的,導致遺傳算法的搜索精度受限,只能搜索到可行解洼地,而無法尋找到最優解。 模式搜索算法通過軸向探測和模式移動,不斷向有利于目標函數值下降的方向探索,在規定精度內能夠求得當前解洼地內的最優解。模式搜索算法對初值敏感,在步長和加速因子較小的情況下,全局尋優性能較差,但由于收縮因子的控制,局部搜索能力較為優異。 遺傳算法和模式搜索均是通過對各參數在其定義域內進行搜索,不需要進行求導、求梯度運算,因此,在處理高維度尋優中具有極大優勢,每增加一個維度,僅是在基因編碼中增加一個基因片斷,整體算法不會有較大改變。相較貝葉斯等算法,該算法求解速度快,實現簡單,增加維度情況下,代碼修改量較小,適合維度的拓展。 因此,通過將遺傳算法和模式搜索算法進行結合,能夠充分發揮兩種算法的優點,求得全局最優解。但是,由于遺傳算法存在早熟問題以及求解過程中的隨機性,直接使用兩種算法求解并不穩定,有概率落入局部最優解中。因此,本文提出一種基于遺傳算法-模式搜索算法的MGAPS算法,可以克服該缺點,保證了算法求解的穩定性。 MGAPS算法設計流程(見圖4)為: 圖4 MGAPS算法設計流程圖 1)初始化相關參數,令j=1、i=1,向量A用于存放結果向量,矩陣M用于存儲由向量A組成的結果矩陣,A=[f,x,y,He,Q],其中f是適應度函數值,Q是源強度,[x,y,He]分別是源的橫、縱坐標和高度。 2)執行遺傳算法,求得一組初始解,存入矩陣T(j,:)=[x,y,He,Q]中,矩陣T的每一行即一組初始解。 3)若j≤L,則令j=j+1,返回步驟2,否則轉步驟4。 4)對求得的L組初始解的每列求均值后形成一個新解向量,即QX=sum(T)/L。 5)將QX作為初始基點,執行模式搜索算法,求得解X=[x,y,He,Q]。 6)計算解X的適應度函數f(X),將求得的值f與解向量X組合成新的向量存入向量A中,即A=[f,x,y,He,Q]。 7)將解向量A作為解矩陣M的一個行向量存入矩陣M中。 8)若i≤K,則令i=i+1、j=1,返回步驟2,否則轉步驟9。 9)將解矩陣M中適應度值f最小的一行解賦值給變量Obj,即Obj=min(M(f)),算法終止,Obj(2∶5)即為所求最優解。 遺傳算法是隨機算法,能夠找到最優解洼地,但也有一定概率找到局部最優解,這種概率通過增加種群可以降到很低,幾乎可以忽略,但為了防止這種小概率事件,通過設計多次循環,優中選優的方式,保證了求解結果在最優解附近,且是最近的解,將該解作為模式搜索算法的輸入,可以提高算法的準確性和運行效率。 構建化學事件危害場景,為后續源項反演分析提供基礎。對連續泄漏的化學危害源,利用高斯煙羽模型進行近似擴散模擬[21]: (1) 式中:C(x,y,z,He)是有效源高為He時(x,y,z)點的濃度;u為風速;σx、σy、σz分別為距離原點x處煙團中污染物在下風方向、側風方向及垂直方向的擴散系數,也即高斯分布的在x軸、y軸、z軸方向的標準差。 為驗證MGAPS的可行性,設置如下場景:1)在2 000 m×600 m范圍內模擬危害源擴散;2)危害源強度Q=5×106g/s,位置為(30 m,50 m,10 m);3)大氣穩定度為D級,相關參數設置見表1[22]所示;4)平均風速為2 m/s;5)在下風向5×6網絡的三維空間中放置探測器,探測器高度可三維空間范圍內任意隨機選取,但考慮到實際應用中,無人機探測器數量較少,大部分探測器安裝于手持儀器或探測車輛上,因此隨機選取5個探測器置于在10~50 m 內隨機高度,其余探測器位于1~5 m高度,如圖5~圖7所示。 表1 擴散參數[22] 圖5 監測點位置俯視圖 圖6 監測點三維空間位置 圖7 三維空間5 m隨機高度下空間濃度分布 實驗環境配置:處理器i5-9300H,主頻2.4 GHz,內存8 GB。 (2) 設(xc,yc,Hec,Qc)為源項的預估值,由遺傳算法或模式搜索算法提供,(xi,yi,zi)為第i個監測點的三維坐標。式(1)為源項橫縱坐標位于原點時的計算公式,因此,(xi,yi,zi)點在以(xc,yc,0)為原點下的坐標為(x,y,z),坐標變換如下: (3) (4) 式中: (5) γ1、μ1、γ2、μ2分別為下風距離小于等于1 000 m時σy、σz的擴散系數,γ3、μ3、γ4、μ4分別為下風距離大于1 000 m時σy、σz的擴散系數。式(5)中(x,y,z)由式(3)求得。 表2 監測點觀測值濃度 計算每個監測點觀測值與計算值的差值平方和,之后,再對所有監測點的差值平方和進行求和,即 (6) 所有可能的解中(x,y,He,Q),使得式(6)最小的解為所求,即式(2)所示。 遺傳算法有4個超參數需要設置[23],即: 1) 種群規模N(N≥1):規模太大會增加計算量,規模太小無法提供足夠多的樣本數量。一般取為20~100。 2) 終止代數T(T≥1):代數太大會導致運行時間過長,代數太小無法求得最優解。一般取為100~500。 3) 交叉概率CR(CR∈[0,1]):概率太大會使種群中的優異個體被破壞,概率太小會使搜索停滯不前。一般取為0.40~0.99。 4) 變異概率MR(MR∈[0,1]):。概率太大會變成隨機搜索,概率太小則不會產生新的基因,導致早熟現象,陷入局部解。一般取為0.000 1~0.1。 模式搜索算法有4個超參數需要設置[24],即: 1) 加速因子α(α>0):因子太大會使模式移動過大,算法無法收斂,因子太小會使搜索停滯。一般取為1~2。 2) 收縮因子β(β∈(0,1)):因子太大會使步長變化緩慢,導致運行時間過長,因子太小會使步長迅速減小導致搜索過早結束,無法求得最優解。一般取為0.1~0.5。 3) 初始步長d(d>0):用于控制沿各軸向探測的步進長度,過大或過小都不利于遍歷軸向搜索。一般取為1。 4) 算法精度ε(ε>0):用于控制模式搜索算法的結果精度,是模式搜索算法的終止條件之一,根據實際需要設置。 為保證MGAPS求解結果的準確性和算法運行效率,經過對以上各參數的反復調試驗證,實現MGAPS算法在三維空間中的求解實現能力,得到算法參數設置如下: 1) 遺傳算法參數設置:種群規模N=20,交叉概率CR=0.4,變異概率MR=0.1,終止代數T=100。 2) 模式搜索算法參數設置:加速因子α=1,收縮因子β=0.5,初始步長d=[1,1,1,1],算法精度ε=10-4。 采用實數編碼,內循環執行L=20次,外循環次數K=10次,運行10次MGAPS算法,結果如表3所示。 表3 MGAPS算法運行結果 通過表3數據可以看出,MGAPS可以有效實現三維條件下源項信息的求解,但耗時較長,作為化學事件應急使用,應盡量減少計算耗時。因此,可以通過調整循環參數優化算法運行時間。不同循環次數下的計算結果如表4所示。 表4 不同循環次數下的運行效率及結果 通過表4可以看出,該算法隨著循環次數的增加,耗時相應增加,但所有組合的結果均較為理想,因此,考慮針對事故應急使用,使用耗時1 min內的組合模式較為合理,即L=5、K=2或K=3,另外,考慮到遺傳算法的隨機性,循環次數較少時,容易出現落入局部最優解的可能,因此,選擇L=5,K=3的組合。 在上述實驗中,使用的測量數據是理論計算數據,較為理想,導致反演結果與設置值幾乎一致。為了更加接近真實環境,通過對測量數據進行白噪聲處理,再驗證算法的反演性能。 3.3.1 對觀測數據增加高斯白噪聲 通過設置不同強度的信噪比,觀察白噪聲對計算精度的影響,結果如表5所示。 表5 不同信噪比下反演結果比較(L=5,K=3) 通過表5可以看出,隨著信噪比的增加,計算結果更準確、精度更高,符合預期。但在低信噪比情況,算法解算效果同樣較為理想。以上結果表明,在測量數據準確的情況,對于不同信噪比,本文算法皆能較好地完成對源項的反算。 3.3.2 降低觀測數據觀測精度 在前述實驗中,所使用的觀測數據為理論計算數據,精度到達了小數點后13位,因此,在加入高斯白噪聲情況,對數據的影響效果不明顯,導致在低信噪比條件下仍能得出較為理想的反算結果。但在實際環境下,所使用的測量儀器并不能達到如此高的測量精度,因此,通過降低觀測數據精度,驗證算法的反算性能,結果如表6所示。 表6 不同觀測值精度下的反演結果比較(L=5,K=3) 通過表6可以看出,在使用理論計算數據情況下,通過降低小數點精度對計算結果的影響不大,這由于本算法采用的是循環迭代算法,并從結果組中搜尋使適應度函數值最小的值作為最優解輸出,因此在多輪迭代后,總能找到最優解,通過以上測試驗證了這一特點,因此,本文算法具有較強的抗干擾能力,確保了算法尋優的穩定性。 以L=5、K=3及未添加噪聲的計算數據為例,演示坐標、濃度的反算變化過程,如圖8~圖12所示(同一顏色*號數據為對應同一次外循環K下的遺傳算法求解值) 圖8 第1次遺傳算法求解 圖9 第2次遺傳算法求解 圖10 第3次遺傳算法求解 圖11 第4次遺傳算法求解 圖12 第5次遺傳算法求解 圖8~圖12顯示了5次利用遺傳算法求解源三維空間坐標及源強的過程,從圖中可以看出,遺傳算法在求解過程中,結果具有隨機性,個別值誤差較大,但大多數以期望值為中心波動。為了降低個別異常誤差對結果的影響,通過將5次計算結果求取算術平均值,則能夠保證結果落入最優解洼地中,將該結果作為模式搜索算法的初值,即可求得精確解。但為了防止小概率落入局部最優解中,通過執行3次外循環模式搜索算法,并取其中1次最好解作為最終解輸出,保證了結果的正確、穩定,消除了隨機性造成的誤差,如圖13所示。 圖13 模式搜索算法求解 從圖13中可以看出,遺傳算法搜索到最優解洼地后,在不同初值條件下,模式搜索算法均能夠收斂于期望值附近,實現了對三維空間坐標及源強的反算。將圖13中的x、y、He值進行合成,形成3次模式搜索算法對源位置的三維空間尋優過程,如圖14所示。 圖14 模式搜索算法空間尋優過程 從圖14中可以看出,利用5次遺傳算法求均值得到的初值位置在一定空間范圍內波動,尚不準確,經過模式搜索算法進一步尋優,能夠收斂于最優值。 在第3節中,使用的觀測數據為理論計算數據,反算結果較為理想。在本節中,以2016年于華北某地開展的SF6示蹤試驗為例,利用實測采集數據,進行源項參數反算,驗證算法的求解性能。 六氟化硫,化學式為SF6,無色、無毒且常溫下化學惰性、光照穩定的氣體,難溶于水、在大氣中天然本底低(1×10-15m3/m3)、不沉降、能與周圍空氣迅速混合,能充分代表大氣運動,用電子俘獲氣相色譜可獲得2×10-13mg3/m3的高靈敏度,是一種較理想的示蹤劑,其示蹤距離可遠達100 km[25]。 大氣擴散示蹤試驗為期6 d,在氣象鐵塔100 m高度(30 m高度為輔)釋放示蹤劑SF6,共進行了23次 釋放,采樣56次,試驗期間風速變化大(風速為0.5~7.9 m/s),試驗覆蓋多種天氣類型(大氣穩定度類型為B、C、D),釋放情況如表7所示。 表7 SF6示蹤實驗與模擬條件 試驗共布設弧線7條,采樣點50個,距地面高度1.6 m,分別為A、B、C、D、E、F和G組,分別負責下風向不同距離的采樣,各組采樣點數如表8所示。試驗區域地形平坦,但由于試驗區域附近地形地貌影響,導致布點位置不是弧形,如圖15、圖16所示為第1次釋放采樣點位置。 表8 采樣點編組 圖15 第1次釋放第1次采樣有效采樣點位置 圖16 第1次釋放第1次采樣有效采樣點位置(調整x軸正向為下風方向) 23次有效試驗,每次的有效樣品采集率如表9所示。在整個試驗中,共采集有效樣品1 633個,每次布設50個點采樣,時間同步采樣。除了第9次(由于釋放高度風速為0.5 m/s)釋放獲取率為35.5%較低外,其他22次都超過了一半,總有效樣品采集率為58.8%。 表9 各次試驗有效樣品采集率 4.2.1 實驗參數設置 遺傳算法:種群規模N=20,變異因子MR=0.95,交叉概率CR=0.5,進化代數I=100,外循環次數K=10,內循環次數L=10。 模式搜索算法:加速因子α=1,初始步長d=[1,1,1,1],收縮因子β=0.5,算法精度ε=1×10-4。 坐標參考系:以釋放鐵塔為原點,以下風向為x軸正方向,以下風向逆時針旋轉90°為y軸正方向,在2 400 m×7 000 m范圍內布設監測點。 4.2.2 算法反算求解 利用算法對56組數據進行反算,結果如圖17~圖24所示。 圖17 源強反演結果 圖18 源高反演結果 圖19 橫縱坐標反演結果 圖20 源位置反演結果 圖23 橫坐標反演相對誤差 圖24 縱坐標反演相對誤差 圖17~圖24分別是源強、源高、橫縱坐標和源位置的反算求解結果與真值的對比圖以及各參數的相對誤差(橫縱坐標相對誤差采用求解值與相應坐標軸范圍的比值)。從結果來看,MGAPS算法能夠對56組實測數據中的大部分進行解算,偏差大多數在100%以內,尤其是前30次的反算結果與真值的一致性較好,偏差大部分在30%以內,這主要是由于大氣環境波動造成的(見表7),第5天和第6天,大氣穩定度以B級別為主,為不穩定狀態,大氣層結不穩定,熱力湍流發展旺盛,對流強烈,對探測數據的采集有較大影響。 4.2.3 模型評價分析 針對模型有效性的驗證,Chang 等[26]提出利用了統計誤差分析方法,該方法被廣泛應用于大氣擴散模型的評價中。 統計誤差分析方法包括:比例偏差SFB、幾何平均偏差SMG、幾何平均方差SVG、標準化均方誤差SNMSE、相關系數SCOR以及SFAC2等統計誤差[24, 26-28]。 SFAC2表示預測濃度與實測濃度之比在0.5~2.0之間的預測數據占總數據的比值。 各統計誤差表達式分別為 (7) SMG=exp(E(lnCo)-E(lnCp)) (8) SVG=exp(E((lnCo-lnCp)2)) (9) (10) (11) 從統計分析看,以上誤差的理想取值分別是:SFB=0,SMG=1,SVG=1,SNMSE=0,SCOR=1,SFAC2=1。Chang等[26]通過對大量擴散模型結果與觀測結果對比,認為可接受的模型應滿足:-0.3≤SFB≤0.3,SNMSE<4,SFAC2>0.5,SCOR>0.7,0.7≤SMG≤1.3,SVG≤4。 以上統計參數的選擇條件:當Co與Cp的值分布在一個很大范圍時,SFB、SNMSE和SCOR受Co或Cp中較大值的影響大,受較小值的影響小。為了公平衡量這些數據的作用,推薦使用對數統計量SMG、SVG。當實測值與預測值分布范圍不大時,應使用SFB、SNMSE、SFAC2和SCOR。本文屬于后者,因此不使用SMG、SVG。 利用MGAPS算法模型預測數據與實際數據進行比對,實測濃度與預測濃度散點圖如圖25所示,在監測點濃度值對比如圖26所示。 圖25 實測濃度與預測濃度散點圖 圖26 預測濃度與實測濃度在監測點的對比 圖25顯示了實測濃度與MGAPS模型預測濃度的散點分布,從圖中可以看到數據點相對集中均勻地分布在紅線的兩側(實測濃度=預測濃度),說明模型的預測結果與實測結果相關性較好。從圖26中可以看出,實測濃度與預測濃度的總體趨勢相同,符合擴散預期特征。 利用式(7)、式(10)、式(11)和SFAC2,進一步對二者進行統計誤差分析,評價模型的有效性,得到結果如表10所示。 表10 MGAPS算法預測值統計誤差 從表10中可以看到,預測結果的統計誤差都在可接受范圍之內,因此,MGAPS算法模型能夠較為準確的預測氣體擴散,并用于化學危害源的源強及三維空間坐標的反算求解。 4.3.1 誤差原因分析 由實測數據反算實驗可知,利用實際監測數據,通過MGAPS算法能夠對在真實環境中的化學危害物質擴散后的危害源位置、濃度及釋放源高度的反算求解,精確度在30%以內,但仍有部分解算誤差較大,甚至無法求解的情況,主要原因有以下4個方面: 1)算法模型誤差。MGAPS算法是通過利用理想狀態下高斯擴散原理對污染物擴散進行求解,但真實環境中需要考慮的實際因素很多,此類誤差可通過深化模型分析解決,但是不可能避免。在大氣環境穩定狀態下,算法求解較為理想,能夠將誤差精度控制在一定范圍內。 2)監測儀器及測量誤差。氣象測量設備、示蹤劑采樣設備、示蹤劑分析設備等測量偏差也是導致計算誤差產生的原因,同時由于在測量過程中,采樣點位置的選擇,周圍環境、遮蔽物等因素,也會導致測量誤差的存在。 3)背景場誤差。由于風向和風速對示蹤氣體擴散有較大影響,試驗區域風向風速多變,示蹤氣體的擴散規律不穩定,導致測量結果差異較大。例如,第1天~第4天,大氣穩定度多為C、D為主,大氣環境穩定,反算結果較為理想,特別是在早上日出前后的測量數據反算效果較好。而第5天~第6天,大氣層結不穩定,在地面的監測結果存在較大誤差,導致求解偏差較大,甚至無法求解的情況。 4)重氣擴散誤差。本文使用理想高斯模型進行計算,適用于擴散機制較為清晰的中性氣體,SF6擴散實驗屬于重氣擴散,其擴散機制復雜,可能導致反算結果誤差較大。下一步,可通過將目標函數更改為重氣擴散模型進行反算性能驗證。 4.3.2 算法適用性 通過以上實驗分析,本算法在大氣穩定度C及以下,風速、風向等大氣環境條件穩定情況下,能夠較好的對危害源相關參數的反算。但由于受限于采樣條件,在大氣穩定度為B及以上時,離危害源較遠的地面監測點采樣結果不理想,未來,可通過增加無人機等手段,通過對空中一定高度的濃度數據進行監測,并反算求解,進一步驗證算法的可行性。 針對化學危害事件后,需要盡快確定危害源參數的現實需求,提出一種基于GA-PS的MGAPS算法,并進行了仿真分析。得出以下主要結論: 1)MGAPS算法基于三維空間探測器收集的危害物質濃度數據,能夠實現對危害源在三維空間的定位和源強的反算。 2)當內循環執行20次、外循環執行10次時,誤差不超過10×10-5要求下,MGAPS算法耗時約為177~323 s。 3)通過優化內循環執行次數與外循環執行次數的組合,可以大幅度提高運行效率。當內循環執行5次,外循環執行3次,誤差不超過10×10-5要求下,耗時可在50 s左右,滿足實用要求。 4)MGAPS算法具有較強的抗干擾能力,通過對觀測數據增加高斯白噪聲、降低觀測數據精度等操作,算法均能穩定求解。 5)MGAPS算法能夠針對大氣穩定度C及以下,風速、風向穩定的大氣環境條件下的實際監測數據進行反算,求解精度在30%以內,基本能夠實現對危害源的有效定位。2 MGAPS算法實現
2.1 MGAPS算法實現思路
2.2 MGAPS算法設計

3 實驗驗證與分析
3.1 化學事件危害模擬場景

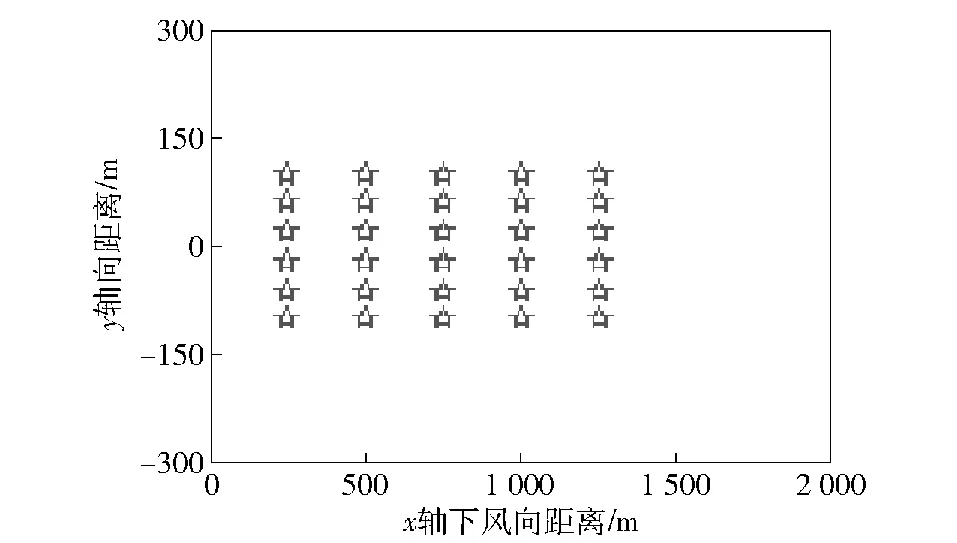






3.2 算法參數設置
3.3 MGAPS算法求解


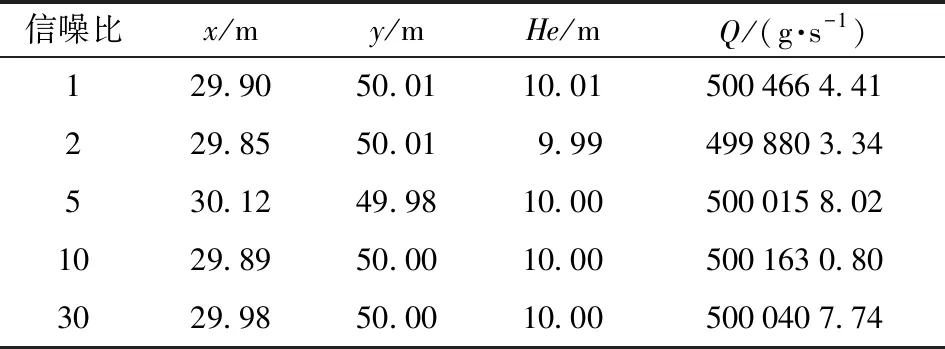








4 實例分析
4.1 SF6示蹤實驗基本情況介紹





4.2 實驗模擬與分析


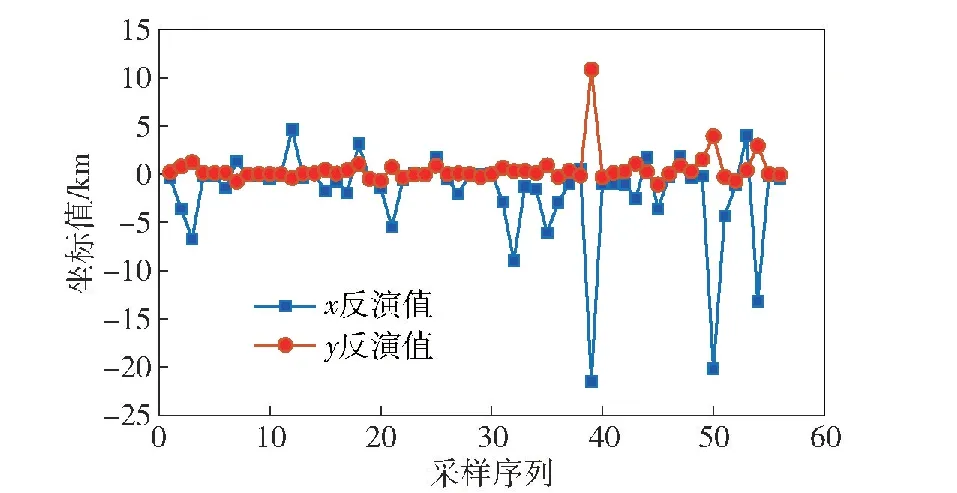







4.3 實驗結果討論
5 結論

