多飛行器協(xié)同任務(wù)分配的改進(jìn)粒子群優(yōu)化算法

王磊, 徐超, 李淼, 趙慧武

(1.北京特種機(jī)電控制研究所, 北京 100012; 2.北方自動控制技術(shù)研究所, 山西 太原 030051)

0 引言

在當(dāng)今軍用和民用領(lǐng)域,飛行器在目標(biāo)搜索、對地攻擊、空中搜救、交通巡查以及快遞運輸?shù)确矫姘l(fā)揮著重要作用[1]。因為單架飛行器無法高效率的完成復(fù)雜任務(wù),經(jīng)常需要使用多個飛行器協(xié)同完成復(fù)雜任務(wù)。因此,多飛行器系統(tǒng)在復(fù)雜的任務(wù)環(huán)境實現(xiàn)靈活的任務(wù),已成為重要研究內(nèi)容[2],多飛行器協(xié)同任務(wù)分配問題已成為飛行器自主導(dǎo)航領(lǐng)域亟需解決的關(guān)鍵問題[3]。

多飛行器協(xié)同任務(wù)分配是指:給定飛行器的種類及數(shù)量,根據(jù)一定的物理環(huán)境信息和任務(wù)要求,將一個或多個任務(wù)分配給一個飛行器,當(dāng)所有飛行器完成所分配的任務(wù)后,整個飛行器編隊的整體效能達(dá)到最優(yōu)[4]。在解決多飛行器任務(wù)分配問題時,需考慮飛行器的任務(wù)能力上限、任務(wù)時序約束以及實時規(guī)劃有效性等要求[5]。理論上,多飛行器任務(wù)分配問題屬于非確定性多項式困難(NP-hard)的排列組合問題。對于大規(guī)模系統(tǒng),難以完全避免組合爆炸問題。目前,研究者提出了多種計算可行的協(xié)同任務(wù)分配算法。文獻(xiàn)[6]提出一種基于“招標(biāo)-投標(biāo)-中標(biāo)”的市場拍賣機(jī)制,設(shè)計了多Agent分布式任務(wù)分配算法。文獻(xiàn)[7]重點研究了實際任務(wù)環(huán)境中存在的不確定性約束條件,提出一種分布式多無人機(jī)協(xié)同任務(wù)分配方法。文獻(xiàn)[8]提出了基于拍賣和一致性原理的分布式任務(wù)分配算法。文獻(xiàn)[9]利用混合整數(shù)規(guī)劃的方法研究了無人機(jī)搜索任務(wù)分配問題,給出問題的最優(yōu)解。智能進(jìn)化算法因為具有靈活、易實現(xiàn)和計算復(fù)雜度低的特點,被廣泛地用于多飛行器協(xié)同任務(wù)分配的研究。文獻(xiàn)[10]在多子群蟻群算法的基礎(chǔ)上,提出了基于分工機(jī)制的蟻群算法求解無人機(jī)協(xié)作多任務(wù)分配問題。文獻(xiàn)[11]建立了蝗蟲仿生算法用于多無人機(jī)搜救任務(wù)。文獻(xiàn)[12]提出一種改進(jìn)遺傳算法(GA),用于集中式在動態(tài)環(huán)境中給無人機(jī)任務(wù)分配任務(wù)。文獻(xiàn)[13]將差分進(jìn)化算法用于解決任務(wù)分配問題。文獻(xiàn)[14]提出基于和聲搜索算法的任務(wù)分配算法。

與其他智能進(jìn)化算法相比,粒子群優(yōu)化(PSO)算法具有較強(qiáng)的尋優(yōu)能力,且魯棒性較強(qiáng)。文獻(xiàn)[15]提出用于調(diào)整PSO算法的主要控制參數(shù)的自適應(yīng)策略,并研究了PSO算法的收斂性。為了進(jìn)一步提高PSO算法在解決任務(wù)分配問題的效率,文獻(xiàn)[16]采用混合整數(shù)規(guī)劃的方法構(gòu)造適應(yīng)度函數(shù)。文獻(xiàn)[17-20]提出了多種用于任務(wù)分配和路徑規(guī)劃的改進(jìn)PSO(MPSO)算法。

本文研究了多飛行器協(xié)同任務(wù)分配問題,提出了一種任務(wù)分配MPSO算法。主要創(chuàng)新點包括:基于粒子連續(xù)性的位置和速度,解碼出離散化的任務(wù)分配方案,即實現(xiàn)了PSO算法連續(xù)性解的離散化;為了防止算法過早陷入局部收斂的問題,根據(jù)模擬退火算法原理,建立一種跳出局部收斂的策略,并將這種策略嵌入到PSO算法的每一次迭代中;與其他算法進(jìn)行了對比實驗,驗證了本文提出的MPSO算法的有效性。

1 多飛行器協(xié)同任務(wù)分配數(shù)學(xué)模型

本文基于水平二維戰(zhàn)場環(huán)境研究了多飛行器協(xié)同任務(wù)分配問題。每架飛行器按照一定的攻擊順序?qū)Φ孛娑鄠€目標(biāo)進(jìn)行打擊,同時目標(biāo)也能偵查、攻擊飛行器,對飛行器具有一定的防空威脅。

假定總共有Nu架飛行器U={U1,…,UNu}和Nt個目標(biāo)T={T1,…,UNt},需要對每個目標(biāo)執(zhí)行一次攻擊任務(wù),因此相應(yīng)的共有Nt個任務(wù)M={M1,…,MNt}。飛行器數(shù)目遠(yuǎn)遠(yuǎn)小于任務(wù)數(shù)目,即Nu?Nt。本文研究的任務(wù)分配問題的目標(biāo)是為每架飛行器Ui指派一個順序攻擊任務(wù)集合Θi:

Θi=〈Mw,1,Mw,2,…,Mw,k〉

(1)

式中:Θi為給飛行器Ui指派的任務(wù),所有任務(wù)Θi就構(gòu)成了一個任務(wù)分配解或方案,i∈{1,…,Nu}。當(dāng)Ui執(zhí)行Θi時,先從初始位置Bi起飛,先執(zhí)行任務(wù)Mw,1, 然后攻擊Mw,2,以此類推,依次攻擊Θi中的任務(wù)。Ui攻擊完最后一個任務(wù)Mw,k后返回初始位置Bi,總航程表示為dis(Θi)=dis(Bi,Tw,1)+Σs∈{1,…, k-1}dis(Tw,s,Tw,s+1)+dis(Tw,k,Bi),其中函數(shù)dis(·)表示兩個任務(wù)的相應(yīng)目標(biāo)或初始位置與目標(biāo)之間的距離。如圖1描述了飛行器U1、U2以及 5個任務(wù)M1～M5的位置坐標(biāo),同時也表示將任務(wù)M1、M2和M4依次分配給了U1,將M3和M5分配給了U2,即一組任務(wù)分配解Θ1=〈M1,M2,M4〉以及Θ1=〈M3,M5〉。

圖1 多飛行器協(xié)同任務(wù)分配示意圖

利用0-1變量xij表示飛行器Ui執(zhí)行任務(wù)Θi時是否執(zhí)行第j個任務(wù)Mj:

(2)

通過為飛行器合理分配攻擊目標(biāo),保證飛行器編隊整體作戰(zhàn)性能最好。實際上,多飛行器協(xié)同任務(wù)分配是個排列組合優(yōu)化問題,需要考慮以下的約束、代價與收益:

(3)

每個目標(biāo)只能指派給一個飛行器,不能重復(fù)分配。此約束表示為

(4)

(5)

3)航程代價。飛行器需要飛行一定航程完成任務(wù)。通過將航程代價指標(biāo)最小化,盡可能地減少資源消耗。飛行器Ui執(zhí)行任務(wù)Θi的航程代價函數(shù)為

minLi=dis(Θi)

(6)

(7)

綜合上述分析,可得飛行器協(xié)同任務(wù)分配問題的數(shù)學(xué)模型為

(8)

s.t.式(3)和式(4)

xij∈{0,1},?i∈{1,2,…,Nu},?j∈{1,2,…,Nt}

式中:s1、s2和s3分別是威脅代價、航程代價以及攻擊收益對應(yīng)的權(quán)重。類似文獻(xiàn)[15]的分析,本文均衡考慮威脅代價、航程代價和攻擊收益,因此設(shè)定s1=1、s2=1、s3=1。

2 基于MPSO算法的多飛行器協(xié)同任務(wù)分配方法

2.1 PSO算法原理

PSO算法中,一定數(shù)目的粒子組成種群,每個粒子代表問題的一個潛在解。每個粒子有兩個屬性:位置和速度。在種群進(jìn)化過程中,粒子需要追蹤兩個極值:一個是粒子自身歷史的最優(yōu)解,稱為個體極值;另一個是整個種群當(dāng)前的最優(yōu)解,稱之為全局極值。所有粒子基于這兩個極值更新位置和速度,從而盡快向最優(yōu)解靠攏。如果問題的解是D維的,那么相應(yīng)粒子的位置和速度都可看做D維向量。假設(shè)粒子Pk在t時刻的位置和速度分別是Yk,t=(Yk,t[1],…,Yk,t[D])和Zk,t=(Zk,t[1], …,Zk,t[D]),它們按照式(9)和式(10)演化:

Zk,t+1[j]=w·Zk,t(t)[j]+c1·Rand1·(pbestk,t[j]-Yk,t[j])+c2·Rand2·(gbestk,t[j]-Yk,t[j])

(9)

Yk,t+1[j]=Yk,t[j]+Zk,t[j]

(10)

式中:w稱為慣性權(quán)重,根據(jù)文獻(xiàn)[15]分析,通常情況下令w=0.721 3;c1和c2是自然常數(shù),通常情況下令c1=c2=2;Rand1和Rand2是分布在[0, 1]之間的隨機(jī)數(shù);pbestk,t是粒子Pk當(dāng)前時刻t的個體極值;gbestk,t是種群當(dāng)前找到的全局極值。在種群進(jìn)化過程中,粒子Pk的任一位置分量Yk[j]被限制在最大位置Ymax和最小位置-Ymax之間,如式(11)所示:

(11)

傳統(tǒng)PSO算法流程如下:

1)設(shè)置粒子種群規(guī)模、最大迭代次數(shù),初始化粒子位置和速度,計算每個粒子的個體極值和全局極值。

2)計算每個粒子的適應(yīng)度函數(shù)值,如果該值優(yōu)于該粒子當(dāng)前個體極值,則更新該個體極值;如果某個體極值優(yōu)于當(dāng)前的全局極值,則更新全局極值。

3)按照式(9)和式(10)更新每個粒子的位置和速度。

4)如果迭代次數(shù)達(dá)到最大迭代次數(shù),則停止迭代,輸出全局極值為當(dāng)前最優(yōu)解,否則,轉(zhuǎn)入步驟2。

2.2 用于多飛行器協(xié)同任務(wù)分配的MPSO算法

利用PSO算法解決多飛行器協(xié)同任務(wù)分配問題,需要解決以下兩個難點:1)任務(wù)分配問題屬于排列組合優(yōu)化問題,其解空間是離散的,而傳統(tǒng)PSO算法只能給出連續(xù)性的解。因此,需要建立PSO連續(xù)性的解與離散化的任務(wù)分配方案之間的一一對應(yīng)關(guān)系,即離散化PSO算法的解;2)PSO算法具有操作簡單、容易收斂的優(yōu)點,但也容易過早陷入局部收斂。為解決上述兩個問題,本文將粒子的位置編碼為一組任務(wù)分配向量,然后將分配向量解碼為一組任務(wù)分配方案,實現(xiàn)了PSO算法連續(xù)性解的離散化。同時,基于模擬退火算法原理,本文提出一種跳出局部收斂的策略,根據(jù)策略運用生成新粒子,解決了局部收斂問題。

2.2.1 編碼與解碼

令粒子的位置和速度都是Nt維向量,即D=Nt,那么解空間也是Nt維。令粒子的位置上限等于飛行器的數(shù)目,即Ymax=Nu;令函數(shù)K(z)表示不大于z的最大整數(shù),例如K(2.3)=2。

為了更好地解決任務(wù)分配問題,將粒子Pk的位置Yk編碼為一列分配向量Ak=(Ak[1],Ak[2],…,Ak[Nt]),

(12)

很明顯,因為Yk[j]∈[-Nu,Nu],可知Ak[j]是整數(shù)且Ak[j]∈[1,Nu]。

算例1考慮一個多飛行器協(xié)同任務(wù)分配問題,其中Nu=3,Nt=14,即將14個不同目標(biāo)T1～T14分配給飛行器U1～U3。很明顯,其解空間是14維。將粒子Pk的位置和速度都限制在[-3, 3]之間,則相應(yīng)的一組的位置和速度如表1所示。根據(jù)式(12)可得Pk對應(yīng)的任務(wù)分配向量Ak,同樣如表1所示。

表1 一個粒子的位置、速度和相應(yīng)的分配向量

算法1:

輸入:分配向量Ak

輸出:任務(wù)分配方案Θi,i∈{1,…,Nu};

1 for (iinNu){

2 for (jinNt){

3 if (Ak[j]=i){

4Ψ(i)=Ψ(i) ∪ {Tj};

5 }

6 }

7Start[i]=Bi,Θi=?,TN[i]=0; ∥初始化

8 }

9Ψ=?;

10 for (iinNu){

11 while (Ψ(i)≠?){

12 選擇Ts∈Ψ(i);

14Start[i]=Ts;

15TN[i]=TN[i] + 1;

16Ψ(i)=Ψ(i) {Ts};

17 將Ts添加到順序集合Θi的末尾;

18 }

19 else{∥當(dāng)前給Ui分配目標(biāo)超過其上限

20Ψ=Ψ∪Ψ(i);

21Ψ(i)=?;

22 }

23 }

24 } ∥初步分配

25 while (Ψ≠?){

27 選擇Ts∈Ψ;

28 選擇Um∈K;

29TN[m]=TN[m] + 1;

30Start[m]=Ts;

31Ψ=Ψ {Ts};

32 將Ts添加到順序集合Θm的末尾;

33 } ∥再次分配

34 輸出Θi,i∈{1,…,Nu};

算法1的數(shù)組Start和TN都是Nu維的,其中,分量Start[i]表示當(dāng)前時刻分配給飛行器Ui的末尾目標(biāo),分量TN[i]表示當(dāng)前時刻分配給飛行器Ui的目標(biāo)個數(shù)。集合Ψ表示受限于飛行器攻擊能力約束、未能分配的目標(biāo)集合。算法1可分為以下3個步驟:

1) (1～9行):根據(jù)分配向量Ak為每個飛行器Ui分配一組目標(biāo)集合Ψ(i)。此時,Ψ(i)中目標(biāo)的個數(shù)可能超過了Ui的攻擊能力上限,并且也沒有確定攻擊目標(biāo)的順序。同時,初始化Start、Θi和TN,使得?i∈{1,…,Nu},Start[i]=Bi,Θi=?,TN[i]=0。

在初步分配過程中,對于U1,因為T9∈Ψ(1),將T9加入Θ1;接下來,Ψ(1)中剩余目標(biāo)T10,將T10加入Θ1的末尾,依次類推,可得Θ1=〈T9,T10,T14,T12,T11〉,其數(shù)量達(dá)到了U1的任務(wù)能力上限,但此時Ψ(1)中還剩余一個未分配的目標(biāo)T13,需要將T13并入Ψ,即Ψ={T13}。同理,可得Θ2=〈T1,T2,T3,T8,T4,〉,達(dá)到了U2的攻擊能力上限,但Ψ(2)中目標(biāo)T7未分配,只能將T7并入Ψ,此時Ψ=Ψ∪ {T7}={T13,T7}。類似的可得Θ3=〈T5,T6〉。

在再次分配過程中,只有U3沒有達(dá)到攻擊能力上限。因此,需要將Ψ={T13,T7}中的目標(biāo)分配給U3。先把T13分配給U3,再把T7分配給U3,即把T13和T7依次添加到Θ3的末尾,可得Θ3=〈T5,T6,T13,T7〉。

因為PSO算法是從初始種群開始進(jìn)化,初始粒子的質(zhì)量會影響算法的收斂速度。為了使得初始種群中粒子分布的更加均勻,本文令例子Pk的位置Yk的每個分量Yk[j]滿足[-Nu,Nu]之間的均勻分布,同理令Pk的初始速度向量Zk[j]也滿足[-Nu,Nu]的均勻分布。

2.2.2 基于模擬退火算法的跳出局部收斂的策略

傳統(tǒng)PSO算法很容易陷入局部收斂。受到模擬退火算法的啟發(fā),提出一種使得PSO算法盡快跳出局部收斂、擴(kuò)大搜尋范圍的方法。這種方法先以某種規(guī)則生成新粒子,然后按照概率函數(shù)判斷是否接受這個粒子的更新。

1)局部搜索啟動準(zhǔn)則:為了平衡算法的對于解空間的開發(fā)和探索的能力,使用概率hk啟動粒子Pk的基于模擬退火算法的局部搜索過程,hk由式(13)計算:

hk=1-0.01×102g/max_g

(13)

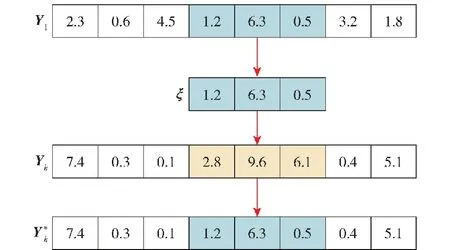
式中:g是當(dāng)前迭代代數(shù);max_g是最大迭代次數(shù)。即對于每個粒子Pk,產(chǎn)生一個隨機(jī)數(shù)r∈[0,1]。如果r

圖2 新粒子位置向量交叉與替換

算法2：

輸入:粒子Pk、個體極值對應(yīng)的粒子Pbestk和全局極值對應(yīng)粒子Pgbest;

輸出:新粒子Pk;

1 計算F(Pk)和F(Pgbest);

2 if (Ω1=F(Pk)-F(Pgbest)>0){

5 if (Ω>0){

6r=random[0, 1];

7 if (r≤exp[-Ω1×Ω])

9 else{

11 }

12 }

13 輸出:粒子Pk;

2.2.3 飛行器任務(wù)分配問題的MPSO算法

本文提出了一種用于多飛行器協(xié)同任務(wù)分配的MPSO算法。首先,限定了粒子的位置大小,根據(jù)式(12)將粒子的位置編碼為一組分配向量。然后,將得到的分配向量作為算法1的輸入,解碼得到一組滿足約束式(3)的任務(wù)分配方案。在PSO算法更新進(jìn)化過程中,每個粒子按照式(8)和式(9)來調(diào)整自己的速度和位置。選擇合適的適應(yīng)度函數(shù),盡可能地減少飛行器付出的威脅代價和航程代價,提高飛行器編隊的總體攻擊收益。同時,提出的新粒子生成策略利用了模擬退火算法的思路,保留了全局極值的有效片段,以一定概率決定是否保留生成的新粒子,有效緩解PSO算法容易陷入局部收斂的問題。

MPSO算法流程如下:

1)初始化種群中的粒子的速度和位置,設(shè)置迭代次數(shù)max_gen,令g=0。計算全局極值和每個粒子的個體極值。

2)對每個粒子Pk執(zhí)行如下的操作:

①執(zhí)行算法2更新粒子Pk;

②根據(jù)式(12)將Pk的位置編碼為分配向量Ak;

③執(zhí)行算法1,將Ak解碼任務(wù)分配方案Θi,i∈{1,…,Nu};

④根據(jù)得到的任務(wù)分配方案,計算適應(yīng)度函數(shù)F(Pk);

⑤更新每個粒子的個體極值和全局極值;

3)根據(jù)式(8)和式(9)更新每個粒子的速度和位置,令g=g+1。

4)判斷迭代是否結(jié)束,若g

5)輸出全局極值及對應(yīng)的任務(wù)分配方案。

3 實例仿真

算例3任務(wù)區(qū)域有15個目標(biāo)T1～T15,3架飛行器U1～U3。目標(biāo)和飛行器的位置、價值、威脅等屬性都是隨機(jī)產(chǎn)生,如表2和表3所示。本文分別用3種PSO算法(MPSO算法、PSO算法、PSO1算法)和一種GA求解此問題,并對比分析實驗結(jié)果。驗證平臺是基于2.3 GHz的Core i9 9880H的MacBook Pro計算機(jī),使用Python編寫程序。其中,MSPO算法是由本文給出的算法;PSO算法利用了本文提出的算法1對粒子進(jìn)行編碼與解碼,但沒有試圖解決局部收斂問題;PSO1算法由文獻(xiàn)[15]給出,粒子的更新過程中沒有修復(fù)粒子對應(yīng)的解,保留了不滿足要求約束條件的解;GA由文獻(xiàn)[4]給出。

表2 目標(biāo)情況

利用MPSO算法、PSO算法、PSO1算法和GA分別求解此任務(wù)分配問題。分別運行10次程序,并記錄平均適應(yīng)度值以及最優(yōu)適應(yīng)度值,圖3給出了運行過程中各個算法的最優(yōu)適應(yīng)度值變化過程。得得到的各個算法最優(yōu)解如表4所示。平均適應(yīng)度值和最優(yōu)適應(yīng)度值如表5所示。從表5中可以看到,MPSO算法給出了最優(yōu)結(jié)果562.85,PSO算法給出次優(yōu)結(jié)果567.44,PSO1算法和GA給出的結(jié)果分別是574.55和563.08。很明顯,MPSO算法要比其余3種算法性能更好。

表4 不同算法得到的最優(yōu)分配解

圖3 系統(tǒng)程序運行適應(yīng)度值變化

因此,無論從最優(yōu)適應(yīng)度還是平均適應(yīng)度來看,MSPO算法都給出了最好結(jié)果。

本文提出的MPSO算法在解碼粒子時修正了對應(yīng)的任務(wù)分配解,使之滿足約束條件,并且引進(jìn)了基于模擬退火算法的跳出局部收斂策略。分析可知:1)MPSO算法在更新粒子時,接受性能好的粒子,以一定概率接受性能較差粒子,而PSO算法不會接受性能較差的粒子。因此,在迭代初期,PSO算法表現(xiàn)要優(yōu)于MPSO算法,但是到算法迭代后期,隨著接受較差粒子的概率降低,MPSO算法體現(xiàn)出跳出局部極值的優(yōu)點,這與圖3中結(jié)果相一致;2)PSO1算法在更新粒子時沒有修正對應(yīng)的解,保留了不可行解,因此與MPSO算法和PSO算法相比,PSO1算法的性能較差,這也在圖3中得到了體現(xiàn);3)GA沒有修正解碼后的解,只保留可行解,因此收斂速度較慢、性能較差。

4 結(jié)論

本文以水平二維戰(zhàn)場環(huán)境多架飛行器多對地面目標(biāo)開展協(xié)同攻擊為研究背景,提出一種用于任務(wù)分配的MPSO算法。得出以下主要結(jié)論:

1)傳統(tǒng)PSO算法給出的解是連續(xù)量,而多飛行器任務(wù)分配解是離散量。為了解決這一問題,本文將粒子的位置屬性編碼為任務(wù)分配向量,并從任務(wù)分配向量中解碼出對應(yīng)的任務(wù)分配解,即實現(xiàn)了PSO算法解的離散化。

2)傳統(tǒng)PSO算法收斂較快,容易陷入局部收斂。為克服這一問題,本文提出一種基于模擬退火算法的跳出局部收斂策略。將這種策略嵌入到傳統(tǒng)PSO算法中,能有效地提升PSO尋優(yōu)的能力。

3)數(shù)字仿真表明,本文提出的MPSO算法性能要優(yōu)于傳統(tǒng)PSO算法以及GA。