高等數學在BOPPPS 教學模式下融入思政元素的教學方法探索*

車晉 盧丑麗 杜建慧

晉中信息學院 山西晉中 030800

0 引言

2016 年12 月，習近平總書記在全國高校思想政治工作會議上強調，高校思想政治工作關系高校培養什么樣的人、如何培養人以及為誰培養人這個根本問題。要堅持把立德樹人作為中心環節，把思想政治工作貫穿教育教學全過程，實現全程育人、全方位育人，努力開創我國高等教育事業發展新局面。同時，新工科對我國理工科教育提出了新的要求。高等數學是理工科大一學生的必修課，也是在現代科學技術、經濟管理、人文科學中應用最廣泛的一門課程。但是目前應用性本科高校的高數教學現狀存在以下一些問題：

1）高等數學課程面對的是大一新生，大一新生是很具有可塑性的，但是我們目前的教學內容體系只注重傳授學生知識，沒有注重培養學生通過學習高等數學來科學解決問題的能力和處理問題的思想；

2）教學方式單一；

3）教師的教學思想和教學觀念沒有顯著改變，在教學過程中拘泥于教材，不能提升學生各方面的素質和能力；

4）在教學中沒有注重培養大學生的國家觀、民族觀、文化觀[1]。

本文對高等數學的教學設計借鑒了加拿大技師技能培訓的BOPPPS 教學模式。BOPPPS 教學模式源于加拿大的教師技能培訓，是一種以教學目標為導向、以學生為中心的教學模式。它由導言（Bridge-in）、學習目標（Objective/Outcome）、前測（Pre-assessment）、參與式學習（Participatory Learning）、后測（Post-assessment）和總結（Summary）六個教學環節構成。BOPPPS 名稱是由這六個教學環節的英文單詞的首字母構成。BOPPPS 是教師進行教學設計及課堂組織教學的一種有效模式，突出以學生為中心，以學習目標為導向的有效教學模式。在BOPPPS 模式的各個教學環節，根據教學內容滲透思政元素，通過思政元素的融入引導學生樹立正確的世界觀、人生觀和價值觀。所以通過有效的課程教學設計和“潤物細無聲”地滲透課程思政元素，使大學生在理論學習中有獲得感，而且能夠通過理論知識解決實際問題，從而充實自我提升自我，解決思想困惑，提升道德水平，形成正確的價值標準，滿足新時代下教育育人發展的需要，這也是本文進行探索和研究的意義所在。

1 教學設計思路

BOPPPS 教學模式與課程思政相融合，就是在BOPPPS 的各個教學環節中，根據課程內容滲透思政元素，達到教學育人的培養目標。具體融合措施如下。

引言（B）：開始上課時，教師通過引入網絡中精彩視頻、時事熱點等吸引學生注意力，激發學生的好奇心和學習興趣，引出本節知識，借助超星平臺發放活動區和群聊互動區開展互動。

學習目標（O）：該階段的目的是讓學生明確本節課需要掌握的目標知識點，掌握學習的重點。可通過板書、PPT 等進行展示。本環節旨在培養學生勇于探索、追求真理、團結協作的素質。

前測（P）：前測的目的是掌握學生的受訓能力，了解學生對本課內容的興趣及先備知識，以便調整后續教學內容的深度和進度，讓課程的目標更加聚焦。一般采用問答、小測驗、集體討論等方式進行。此環節要求學生根據課前任務單，觀看微課視頻資料等內容，了解相關數學發展史等，激發和培養學生追求真理的責任感和使命感。

參與式學習（P）：此環節是BOPPPS 教學模型最核心的理念，體現以學生為中心的教學理念。在講清楚概念、重點、難點等知識點后，可以采用報告、分組討論、角色扮演、專題研討、案例分析等各種有趣的方式讓學生參與到教學中去，理解數學思想，透過現象看本質，揭示其所蘊含的普遍規律、哲學思想等思政元素，使學科內容更有深度，此環節不僅培養了學生嚴謹思維能力，幫助學生樹立正確的世界觀和價值觀，同時，強化了學生的語言表達能力、溝通能力及合作能力等。

后測（P）：后測試判斷學生是否達到預期的學習目標，目的是驗收學習成果。此環節可提前在學習通平臺設置測試題、借助超星平臺開展搶答、測驗等活動，激發學生學習的積極性，并根據評估結果進行教學反思，及時調整教學設計，從而更好地達到教學目標。

總結（S）：此環節的目的在于歸納總結本節課的知識點和清理知識脈絡，進一步加深學生的印象。與傳統教學模式不同的是，BOPPPS 模型更加強調由學生自己進行知識的歸納總結。教師可以在學生總結的基礎上做提升，將數學體現的思想與學生的人生經歷、成事之道等聯系起來，幫助學生樹立正確的人生觀；另外，學生可以課下搜集與本節課內容類似的其他實際案例，自主延伸學習，拓展本節內容，增強學習興趣，明確學習目標，自覺地學習科學文化知識。培養學生探索創新的科學精神，為祖國的建設添磚加瓦。

采用BOPPPS 教學模式，將課程思政融入BOPPPS模式的教學環節中。思政元素的挖掘大概可以從這幾個方面出發：可以通過提煉高等數學課程中所蘊含的人文精神、社會責任、愛國情懷等，樹立和踐行社會主義核心價值觀，逐步增強學生的社會責任感、使命感和愛國熱情；或者結合數學史和數學文化，貫徹數學精神，感受數學魅力，培養數學素養，使學生堅定文化自信，繼承和發揚中華民族的優秀文化傳統；借助高等數學課程具有科學嚴密、邏輯性強等特點，引導學生堅守科學理念，強化數學意識，在教學過程中逐步提升學生精益求精、勇于創新的品質。在BOPPPS 教學模式的各個環節中融入思政元素的框架圖如圖1 所示。

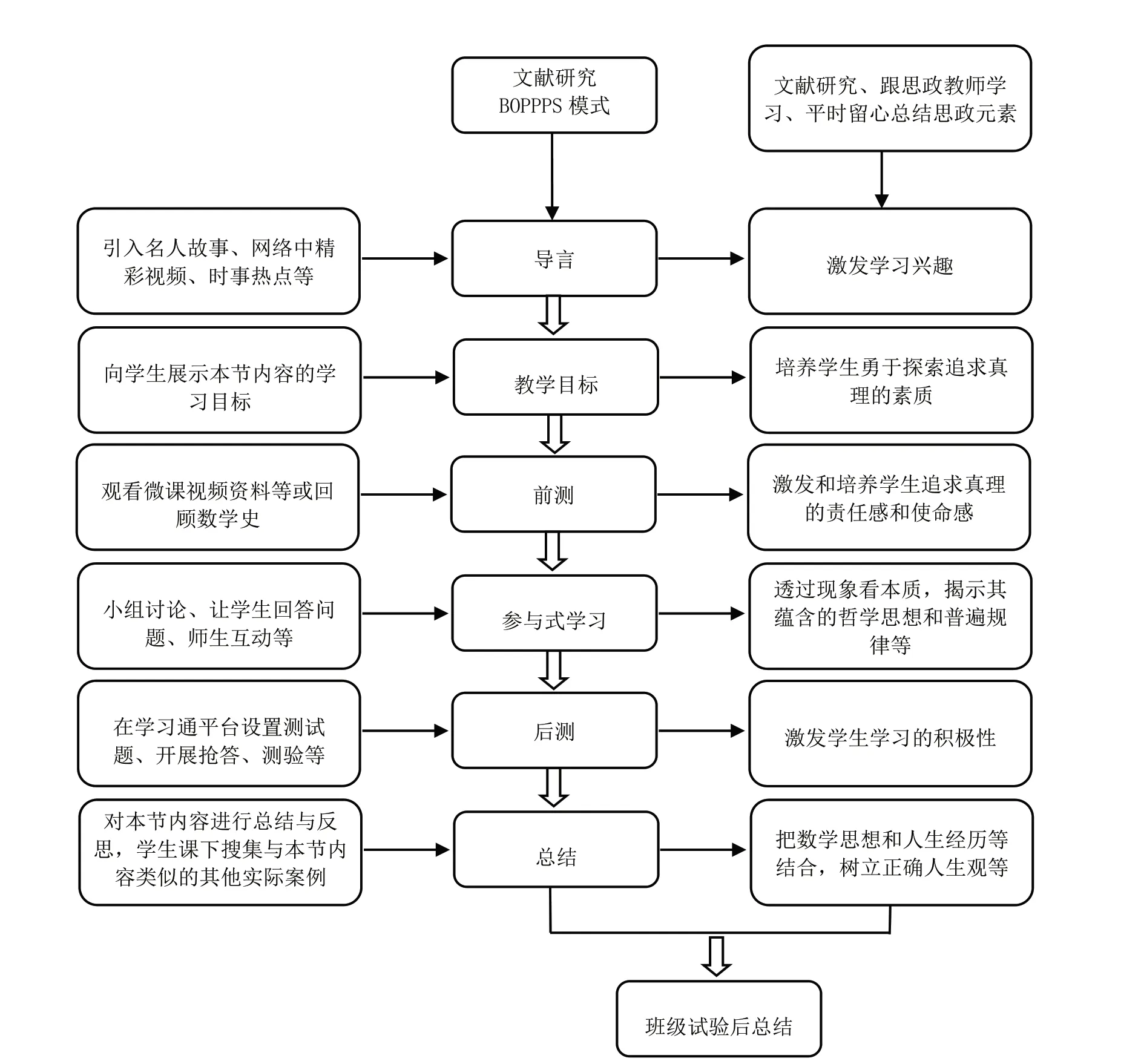
圖1 在BOPPPS 教學模式的各個環節中融入思政元素的框架圖

2 以常數項級數的概念為例

回顧數學歷史素材：2 400 多年前，希臘數學家芝諾（Zeno）提出幾個著名的悖論，其中一個叫做“二分說”的悖論聲稱：一個人永遠無法從甲地走到乙地。芝諾的推理是：這個人想從甲地到乙地，他首先要通過整個路程的一半，然后又要通過剩下的路程的一半，以后永遠要通過剩下路程的一半，把整個路程的長度設為1，則所走的路程為1/2+1/4+1/8+1/16……，這個過程沒有完結，所以這個人不可能從甲地到達乙地。換句話說，芝諾將這段路程劃分成無限多段，他認為一個人不可能在有限的時間內通過無限多段路程。

事實上，一個人能夠從甲地走到乙地，可芝諾的推理似乎也有一些道理。這一悖論的提出是針對事物無限可分的觀點。當時的數學家在沒有極限等抽象概念支撐的情況下，并不能嚴格準確地解釋這究竟是不是真理。如何解釋芝諾悖論留給學生下去查閱相關資料[2]。而現在的任務是探究1/2+1/4+1/8+1/16……如果一直加下去，它的和是否存在。通過此悖論的引入，調動學生學習的積極性，培養學生堅持真理、勇于探索的求真精神。

2.1 教學目標

通過PPT 向學生明確本節課的學習目標：理解常數項級數的定義；掌握常數項級數斂散性的概念；會用級數斂散性的概念判斷級數的斂散性；能夠用常數項級數斂散性解決一些生活中的實際問題，從而認識到數學是有用的。采用學生為主體的教學方式，讓學生對這堂課感興趣，以飽滿的熱情投入課堂中，借此培養學生主動思考問題，探索問題的能力，提高學生對待學業的認真態度與完成學業的信心。

2.2 前測

提前在上課前發布任務，莊子在《天下篇》中寫道：“一尺之棰，日取其半，萬世不竭，一直截下去，得到的總長度為：1/2+1/4+1/8+1/16…，這個和是否存在，如果存在，我們采用什么方法計算它的和。看看學生是否能想到無限項的和可以通過有限項和的極限來進行計算。

通過前測的學習，學生已經可以理解常數項級數的定義、部分和數列、會無窮多項的和。

2.3 參與式學習

接下來教師給出幾個常數項無窮級數的例子，例如：

學生分組討論這兩個級數的和分別是多少，把第三個級數的和留在課下讓學生先自己去思考解決。然后學生把分組討論的結果上傳到學習通，在學生討論的過程中，教師可以參與到其中，以便了解學生在解答的過程中存在的問題。通過分組討論發現級數的和存在，而級數的和為sn=1+2+3+…+n=n(n+1)/2 的極限為不存在，那怎么定義級數和的存在性呢？

教師進行總結，想要求無窮多項的和，可以先求有限項和，然后求項數n→∞的極限。總結出級數收斂與發散的定義，即：如果級數的部分和數列{sn}有極限s，即，則稱無窮級數收斂，這時極限s叫做這級數的和，并寫成；如果{sn}沒有極限，則稱無窮級數發散。

2.4 后測

學生掌握了級數斂散性的概念后，教師在學習通發布隨堂練習。

【例2】某人耳朵感染，每4 h 服用一次氨卡西林，每次服用200 mg,在一個4 h 的區間內，人體在該區間的末期將存留開始時人體所含該藥量的12%,請問長期服用該藥，人體中該藥物的含量為多少[3]？

解：設Qn表示剛剛服下第n次藥時人體中氨卡西林的含量（以mg 為單位），則Q1=200，Q2=200+200·(0.12)，Q3=[200+200·(0.12)]·(0.12)+200=200+200·(0.12)+200·(0.12)2，Qn=200+200·(0.12)+200·(0.12)2+…+200·(0.12)n-1。

這是一個首項a1=200,公比q=0.12 的等比數列的前n項的和，因此如何病人長期服用此藥，剛服下第n次藥時人體中氨卡西林的含量為：

減去剛剛服下的200 mg,說明人體內殘留的藥物含量為27.27 mg,由此可以看出，定期給一個病人服用某一劑量的藥物，由于新陳代謝的作用，總有一些藥物被排出，而人身體中該藥物的含量將趨于一個穩態。

2.5 總結

通過本節課的學習，學生掌握了常數項級數的概念、斂散性的概念、會求無窮多個常數的和，并且會用本節課的知識解決一些實際的問題。

S=1-1+1-1+…=(1-1)+(1-1)+…=0

或者S=1-1+1-1+…=1-(1-1)-(1-1)-…=1

甚至1-S=1-(1-1+1-1+…)=1-1+1-1+…=S

即S=1/2

發現用不同的方式給此級數加括號后得出的和是不相同的。出現這些錯誤的原因在于有限個數的加減法對于無限個數是不成立的。通過對本題的學習，學生深刻感受到對于新的問題，明白不能采用慣有的思維進行思考，需要持謹慎認真的態度，從而培養學生不怕挫折，追求真理，積極向上的品質。

3 教學效果評價

引入著名的芝諾悖論以及關于格蘭迪級數和的爭論，可以使學生對數學家及數學家的想法產生更深入的了解，體會數學家追求真理的過程并不是一帆風順的，而是經歷了千錘百煉。通過這些事跡鼓勵學生不怕困難，迎難而上的做事態度。同時，推翻悖論的過程會激發學生的求知欲。學生自己查閱資料，可以拓寬自己的知識面，感受數學的發展史，深刻地認識數學的偉大與嚴謹。前測環節引用我國古代數學史上的割圓術，增強學生的愛國情懷和文化自信。

一改以往灌輸式的教學，本文采用BOPPPS 的教學模式，以學生為主體，讓學生真正參與到課堂中，激發了學生思考問題的興趣，提升學生的思考能力。課堂氣氛活躍，學習的積極性明顯提高，學生會積極主動地思考問題，而且發現數學其實沒有想象中的那么枯燥。

在后測環節讓學生通過本節知識來解決生活中的實際問題，激發學生的學習興趣，然后將教學目標進行了升級，讓學生自己發現和挖掘與本節內容相關的生活常識，讓學生充分感受到數學存在于生活中的方方面面。

本節課采用線上+線下的教學方式，網絡資源豐富，教學方式靈活多樣，充分鼓勵學生積極參與教學過程。前測、參與式學習、后測、作業等都用到了網絡教學平臺，方式靈活，學生不容易走神，很大程度提高了課堂教學效率。

4 結束語

參與式學習的教學真正地實現了以學生為主、教師為輔的教學方式。后續高等數學的其他知識點的教學也會采用這樣的教學方式，讓學生主動積極地學習。在合適的教學環節融入思政元素，引導學生于生活、歷史文化中發現數學之美，改變學生原來對數學課程枯燥難懂的固有印象，在時政、科學前沿、專業應用中、人生經驗中體會數學的重要性，培養學生的開放性思維，幫助學生樹立正確的世界觀、人生觀、價值觀，激發學生實現中華民族偉大復興的責任感。